基于小波包能量谱的微电机故障检测方法研究
2017-10-18胡文明陈胜义
胡文明,陈胜义
(湖南人文科技学院,湖南娄底417000)
基于小波包能量谱的微电机故障检测方法研究
胡文明,陈胜义
(湖南人文科技学院,湖南娄底417000)
提出了一种基于小波包能量谱的微电机故障检测方法。测试了微电机在几种不同故障类型下的振动信号,利用小波包变换的分解和重构算法,计算出各子频带的能量谱,并进行归一化处理。各频带信号的能量变化包含着丰富的微电机运行状态信息,在正常情况和故障情况下,小波包分解后各频段信号的能量有明显差异,以频带能量谱构造的特征向量可以建立能量变化到故障的映射关系。初步实验结果表明,小波包能量谱可应用于微电机故障检测。
微电机;小波包;能量谱;故障诊断
1 引言
微电机振动信号携有大量的电机运行状态信息,对其产生的振动信号进行分析处理是电机检测中最有效、最常用的手段。一般来说,故障振动信号是非平稳信号,其特性和时间有关,故处理这些振动信号必须进行时频分析。传统的信号处理方法,如快速傅立叶变换(FFT),仅能有效地分析平稳信号,从时域或频域给出信号的平均结果,而无法同时兼顾信号在时域和频域的局部和整体特性。因此,找到一种既能够反映频域特征又能够反映时域特征的方法是处理非平稳振动信号的关键。任何信号都能被小波包分解成一个由小波平移、伸缩而成的一组基函数上,实现信号在不同频带、不同时刻合理分离,为信号故障特征频率的分离、微弱信号的提取提供了高效有力的工具。
2 小波包分解算法
2.1 由正交小波分解推广到小波包分解
如果由基本小波φ(t)生成的二进制离散小波[3,4,5,6]

构成L2(R)的标准正交基,则有s(t)∈L2(R)的正交小波分解。
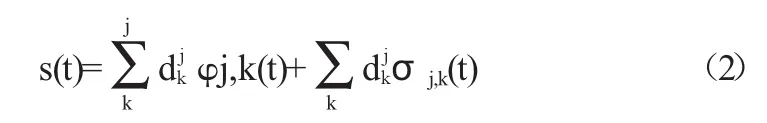
式中:J为分解层数,djk为尺度系数,σj,k(t)为基本小波所得的二进制正交尺度函数:

为了进一步推广二尺度关系,定义下列递推关系:

式中:hko,hk1,为滤波器系数。
当n=0时,d0(t)=σx和d1(t)=φx,则称以上所定义的函数为正交尺度函数d0(t)=σx所确定的小波包,这就把正交小波分解推广到小波包分解。
2.2 小波包能量谱分析
按能量方式表示的小波包分解结果称为小波包能量谱。
假设原始信号为f(x),fi,j(tj)为f(x)小波包分解第i层分解点(i,j)的重构函数,根据parseval能量积分等式,其在时域上的能量:
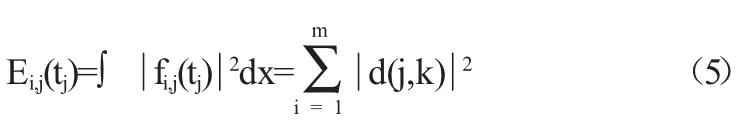
其中,为小波包分解第i层第j节点的频带能量,m为采样点数,为重构信号离散点的幅值。
3 微电机振动信号小波包分析
一般情况下,微电机运行出现故障时,各子频带内信号特征会有较大变化,以频带能量谱构造一个特征向量建立能量变化到故障的映射关系。将故障信号与正常振动信号在不同频段重构信号的能量进行比较,分析能量的分布情况,绘出表征故障的能量监测表,确定发生故障的频段范围,从而诊断出故障类型。
3.1 微电机振动信号的采集
信号的采集系统由ULT2404/V加速度传感器、NI公司的USB4431采集卡(含信号调理模块)和信号处理软件labview三部分组成,其系统结构框图如图1所示。

图1 系统结构框图
利用上述系统采集微电机在正常情况、机壳里面含有铁屑和机壳支架变形三种情况下的振动信号,为微电机故障检测提供数据支持。
3.2 微电机振动信号的时域分析
通过对采集到的微电机振动信号若干组数据进行分析,借助labview软件的高级信号处理包对其处理,绘出各种状况下微电机振动信号的时域波形如图2所示,其中Sign1为正常电机振动信号,Sign2为机壳里面含有铁屑的电机振动信号,Sign3为机壳支架变形的电机振动信号。从时域图中可以看出,虽然各种信号之间有差异,但是并不明显,所以很难从时域上得出诊断结果。

图2 各种状况下微电机振动信号
3.3 微电机振动信号的小波包分析
根据小波包分解原理,利用labview提供的函数对微电机振动信号进行四层小波包分解,采用的分解小波基是db3。图2到图4给出了三种信号小波包四层分解后各频段的重构信号,经过小波包四层分解后各频段代表的频率范围如表1所示(由于信号能量绝大部分都集中在低频段,故只列出8个节点)。为了便于处理分析,小波包所分析的各种情况下的振动信号均采用采样频率为2KHZ,数据长度为2000。
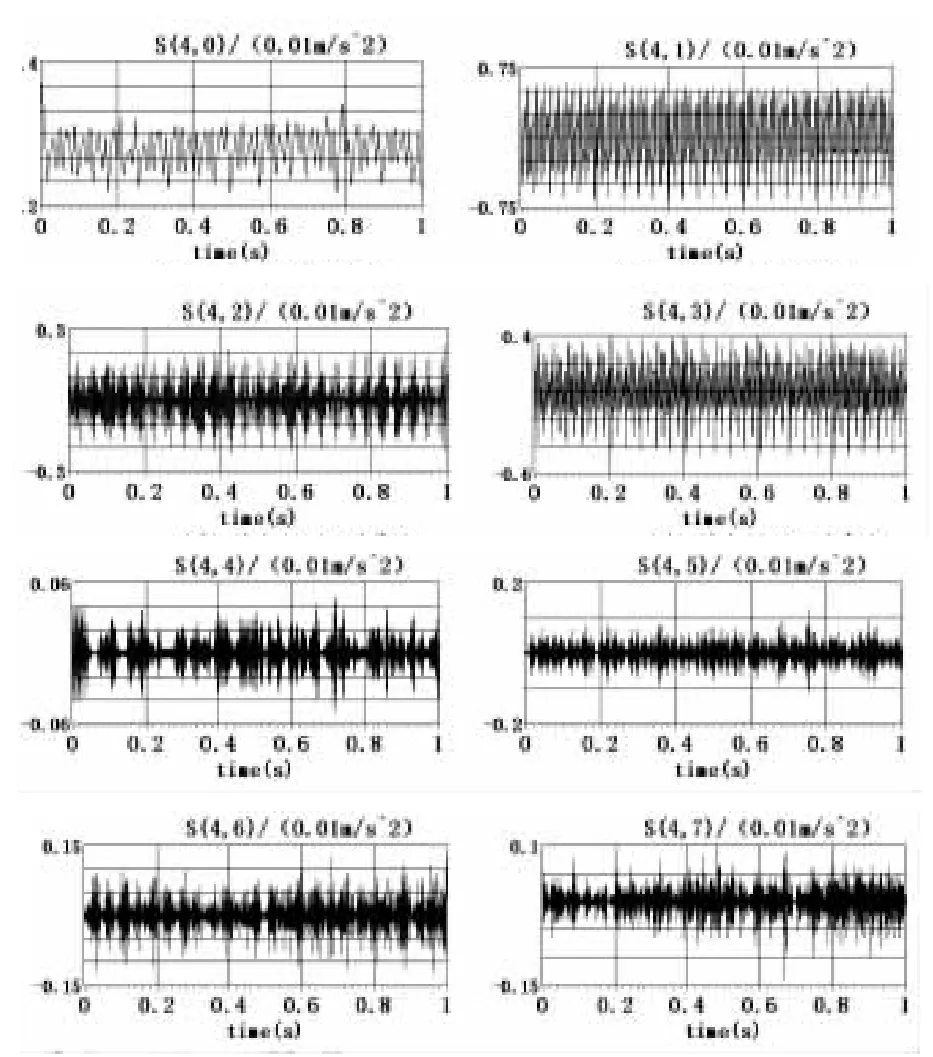
图3 Sign1四层小波包分解重构信号
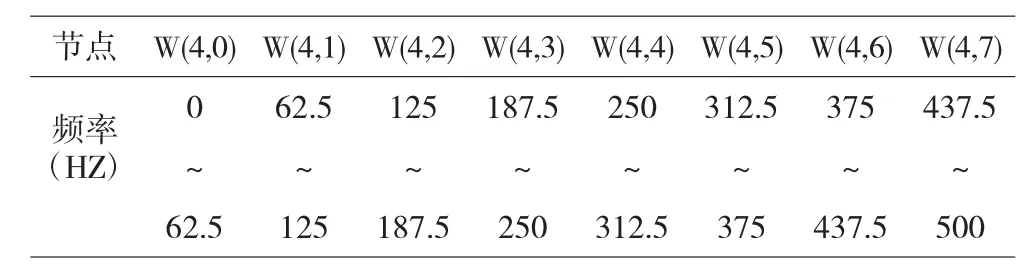
表1 小波包分解各节点频率范围
为了突显出故障特征,根据公式(5)将小波包分解后的重构信号进行能量谱分析,16个频带的能量形成一个16维向量,为了便于比较不同状态下各个频带能量的所占比率,将各子带能量归一化处理后得到故障信号的能量特征向量。表2为前八个子频带能量占总能量的百分比。
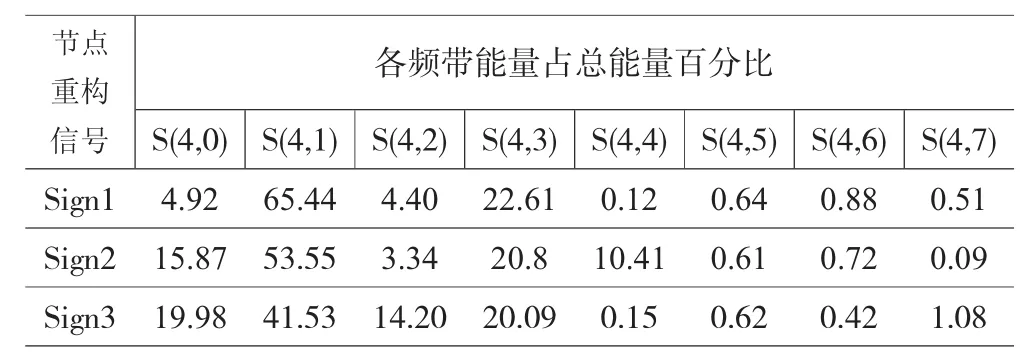
表2 各频带能量占其总能量的百分比
通过对比表2各种情况下重构信号的百分比,可得出如下结论:
(1)Sign2在低频段S(4,0)子空间(0~62.5kHz)内的能量变化非常明显。故障信号能量在该频段所占比例明显升高,即由4.92%升高到15.87%,说明0~62.5Hz是该故障信号的主要特征频带。
(2)其余频带的能量在故障前后虽然也有所变化,但由于它们的能量百分比很小,因此不予考虑。
(3)Sign3在S(4,0)子频带(0~62.5Hz)和S(4,2)子频带(125~187.5Hz)能量明显变大,而S(4,1)子频带能量所占比率下降明显,说明0~62.5Hz和125~187.5Hz是故障信号的主要特征频带。
通过对重构信号能量谱分析,判断发生故障的频段范围,从而判断微电机是否发生故障以及为何种故障。同时由能量谱作构成的信号特征向量,可为微电机故障断诊断提供依据。
4 结语
基于小波包分解与重构的分析方法,能够在不损耗信号能量情况下将振动信号分解到一个由小波伸缩、平移而成的基函数族上,得到分布在不同频带内的分解信号,在时域和频域均具有局部化的分析功能,有利于从复杂振动信号中分离出故障特征。
小波包分解后重构信号的能量谱能够同时反映信号在特定时间和特定频带的信息。利用能量谱可以直观地识别出故障的特征频带,有利于进一步量化分析。
将小波包分解、重构技术与能量谱结合起来的小波包能量谱故障诊断方法可以很好地诊断故障。用该方法对实测微电机振动信号进行处理,实验结果表明效果良好,可以比较直观地反应各频带能量变化情况。
[1]曹衍龙,程实,杨将新.基于小波包的松动件质量估计方法[J].机械工程学报,2010,46(22):1-5.
[2]王江萍,孙文莉.基于小波包能量谱齿轮振动信号的分析与故障诊断[J].机械传动,2011,35(1):55-58.
[3]何芸.基于LabVIEW的发动机振动信号采集系统[J].制造业自动化,2010,32(9):195-198.
湖南人文科技学院校级青年基金(2015QN01)湖南省教育厅科学研究一般项目(16C0827)。
胡文明(1987-),硕士,主要研究方向:过程装备的高效节能与可靠性。
