映射网格在缺口件多轴疲劳寿命预测中的应用

孙 然, 金 丹

(沈阳化工大学 能源与动力工程学院， 辽宁 沈阳 110142)

映射网格在缺口件多轴疲劳寿命预测中的应用

孙 然, 金 丹

(沈阳化工大学 能源与动力工程学院， 辽宁 沈阳 110142)

基于缺口件疲劳试验结果，采用ANSYS软件进行模拟计算，比较自由网格和映射网格对模拟结果的影响.模拟结果表明：在相近的单元数和节点数下，映射网格的计算时间仅为自由网格计算时间的一半；两种网格形式模拟得到的缺口根部应力值相近.将等效应变值作为损伤参量进行疲劳寿命预测，3个缺口半径下映射网格的预测结果均优于自由网格的预测结果；自由网格对于缺口半径为0.09 mm的损伤参量预测结果偏高程度达3倍，但随着缺口半径的增加，两种网格预测结果的精度均有所提高.

缺口件； 自由网格； 映射网格； 疲劳寿命预测

在许多工业领域中，由于结构的复杂性、多方向的外载或是缺口等因素的作用，结构件通常承受比例或非比例的多轴应力状态，因此多轴疲劳问题的研究成为各国学者关注的焦点[1].随着计算机硬件及软件技术的发展，有限元方法在力学、电学、光学等领域内得到了广泛应用，网格划分技术已成为有限元研究中一个重要的方面[2-4].近年来，针对网格化分技术对有限元计算效率、计算精度、误差率等研究取得一些成果[5-11].文献[7]采用粗网格形式对箱梁三维实体进行了有限元分析，粗网格形式较无网格形式有效提高了有限元分析的计算效率.文献[8]应用H网格和自由网格计算了注塑机机械手的横梁变形量，得出了提高网格密度或单元阶次可提高模拟结果精确性的结论.采用四边形网格划分技术和自由网格划分技术对边坡稳定性问题的研究见文献[9].文献[10]比较了自由网格、局部加密网格和整体加密网格3种划分方式对狗骨式刚性连接非线性分析精度的影响，结果表明，在同等计算精度下局部加密网格大大缩短了计算时间.同时，采用AMA方法并结合局部和全局优化技术可以提高映射网格计算的有效性和效率[11].

考虑到网格形式对计算结果的影响，本文在Mod.9Cr-1Mo钢不同缺口半径多轴疲劳试验结果的基础上，采用映射网格和自由网格形式进行模拟计算，基于模拟得到的缺口根部的损伤值，进行疲劳寿命预测.

1 疲劳实验

试验材料为Mod.9Cr-1Mo铁素体钢，材料屈服强度σy=500 MPa，杨氏模量E=200 GPa，泊松比μ=0.3.选用棒材进行试验，具体试件尺寸如图1所示，缺口半径r分别为0.6，0.2和0.09 mm，标距段距离8 mm.具体试验过程见文献[12]，从路径0到路径10共11个路径，本文选取其中单拉路径(Case 0)、比例路径(Case 4)和圆路径(Case 10)进行模拟计算.

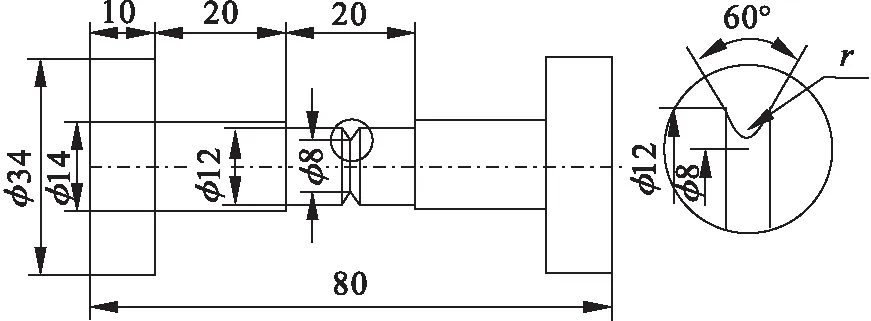
图1 试件尺寸

2 有限元模型的建立

使用ANSYS软件建立缺口试件的三维有限元模型.取试件标距段长度进行建模，根据试件结构特点，创建缺口试件二分之一的轴向截面，选择surface154单元创建面网格.由于缺口根部存在应力集中，分别用自由网格和映射网格对缺口根部区域进行细化.采用计算精度较高、边界为曲线的20节点六面体单元Solid 186进行计算.比较两种网格形式对计算结果的影响.

2.1 自由网格

自由网格划分时通过边长及曲率控制网格的质量.通常情况下，利用智能尺寸控制技术自动控制网格的大小和疏密分布，也可人工设置网格的大小并控制疏密分布.对于复杂的几何模型，这种分网方法省时省力，但单元数量会很大，降低了计算效率[13].

针对本文所用模型，缺口半径为0.6 mm时，等分线分为30份，比率为0.1，采用周向每15°为一份，径向每0.3 mm为一份，共得到7 525个单元，29 669个节点.针对缺口半径为0.2 mm和0.09 mm做同样的细化处理.研究表明，应力集中现象随着缺口半径减小而更加明显，所以缺口半径为0.2 mm和0.09 mm的模型等分线分为40份，比率为0.1，缺口半径为0.2 mm时得到12 475个单元，50 301个节点；缺口半径为0.09 mm时，得到38 491个单元，153 965个节点；缺口半径为0.6 mm的自由网格划分结果见图2(a).

2.2 映射网格

映射网格划分是通过指定单元的边长、网格数量等参数对网格进行控制[14].为方便对两种网格形式进行对比，通过对映射网格的参数进行控制使得缺口半径相同时，两种网格形式下的节点数和单元数相差不多.

缺口半径为0.6 mm时，将等分线分为30等份，轴向约1 mm一份，周向每15°为一份，径向每0.3 mm一份，共得到7 500个单元，29 581个节点；缺口半径为0.2 mm时得到12 496个单元，50 394个节点；缺口半径为0.09 mm时得到38 412个单元，153 891个节点.缺口半径为0.6 mm的映射网格划分结果如图2(b)所示.与图2(a)相比较，图2(b)得到的网格更为整齐.

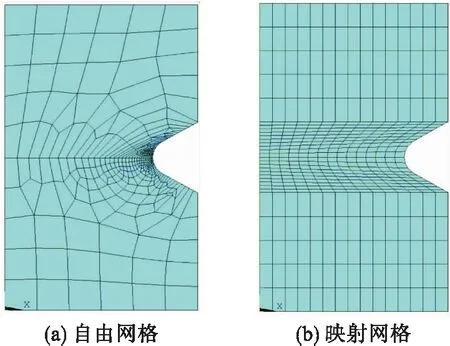
图2 自由网格与映射网格下建立的模型

2.3 模型选择

两种网格化分方法下，材料的弹塑性性质均采用多线性随动硬化模型、Von Mises屈服准则和单轴循环应力应变曲线来描述，材料循环应力应变曲线定义见方程(1).

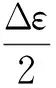
(1)

式中：E为弹性模量，K为循环硬化系数，n循环硬化指数，其值分别为K=1 087和n=0.135，由单轴试验数据拟合得到[12].

2.4 有限元加载

利用ANSYS的function功能将各个路径写入.选择柱坐标系进行拉扭应变加载，将试件一端刚性固定，约束所有自由度；另一端面的所有节点上施加轴向位移，最外层圆周节点上施加周向位移，施加的轴向位移量和周向位移量依据试验时加载的轴向和拉扭应变量计算得到.为获得精确的模拟结果，加载方式采用函数加载，且每个循环内取100个载荷子步.

3 模拟结果比较

利用上述模型针对缺口半径0.6 、0.2和0.09 mm试件的单拉路径、比例路径和圆路径进行模拟计算，比较自由网格和映射网格对模拟结果的影响.

在前期处理中，两种网格下所建立模型的时间大致相同.在计算过程中，3个路径下，自由网格模拟时间约为30～40 min，而映射网格模拟时间仅为自由网格的50 %.但两种网格方式下得到的应力值相差不多，以缺口半径0.6 mm为例，单轴路径下，模拟得到的缺口根部附近的平均等效应力云图如图3所示.

图3 自由网格与映射网格下应力云图

自由网格下缺口根部应力值为450 MPa，而映射网格为448 MPa，两者仅相差0.4 %.比例和圆路径下，自由网格和映射网格模拟得到的缺口根部的应力值分别为478和464 MPa、440和438 MPa，两种网格形式下的误差仅为3 %和0.4 %.虽然缺口根部处存在明显的应力集中，但随着距离缺口根部距离的增加，应力迅速下降，即缺口根部附近存在较大的应力梯度.

4 疲劳寿命预测

将模拟得到的缺口根部的Von Mises等效应变值作为损伤参量进行疲劳寿命预测，预测结果见图4.

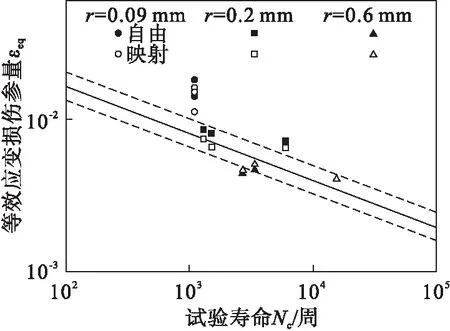
图4 疲劳寿命预测结果

从图4可以看出：无论何种网格形式，等效应变法对于较大缺口半径给出了较好的预测结果，缺口半径0.2 mm和0.6 mm的预测结果基本位于2倍分散带内；对于缺口半径为0.09 mm的损伤参量计算结果普遍偏高，最高程度达3倍；对于3个缺口半径各个路径下，映射网格下的预测结果均好于自由网格的预测结果.从图3的应力云图中可以看出：尽管缺口根部处存在明显的应力集中，但缺口根部附近亦存在较大的应力梯度，仅将缺口根部处的应变值作为损伤参量进行预测必然会得到偏于安全的寿命预测结果，这一点在小缺口半径下表现更为明显.

5 结 论

基于不同缺口半径的多轴低周疲劳试验结果，采用有限元进行模拟计算，得到如下结论：

(1) 比较自由网格和映射网格对模拟结果的影响，针对3个缺口半径，相近的单元数和节点数下，映射网格的计算时间仅为自由网格计算时间的一半.两种网格形式模拟得到的缺口根部应力相差仅为3 %.

(2) 将等效应变值作为损伤参量进行疲劳寿命预测，对于3个缺口半径，映射网格的模拟结果整体优于自由网格的模拟结果；自由网格对于缺口半径0.09 mm的损伤参量预测结果偏高程度达3倍，但随着缺口半径的增加，两种网格预测结果均有所提高.

[1] ARIVAZHAGAN B,SUNDARESAN S,KAMARAJ M.A Study on Influence of Shielding Gas Composition on Toughness of Flux-cored Arc Weld of Modified 9Cr-1Mo (P91) Steel[J].Journal of Materials Processing Technology,2009,209(12/13):5245-5253.

[2] 闵卫东,唐泽圣.有限元网格划分技术[J].计算机研究与发展,1995,32(7):37-42.

[3] 关振群,宋超，顾元宽，等.有限元网格生成方法研究的新进展[J].计算机辅助设计与图形学学报，2003,15(1):1-14.

[4] 李娜.空间网格结构几何形态研究与实现[D].浙江：浙江大学,2009：1-12.

[5] TOSUN S,OZTURK O,OZKAN E,et al.Application Mapping Algorithms for Mesh-based Network-on-Chip Architectures[J].The Journal of Supercomputing,2015,71(3):995-1017.

[6] ROCA X,SARRATE J.Least-Squares Approximation of a Affine Mappings for Sweep Mesh Generation Functional Analysis and Applications[J].Engineering with Computers,2013,29(1):1-15.

[7] 尧云涛,肖汝诚.粗网格划分下的箱梁三维实体有限元分析方法[J].工程力学,2010,27(3):67-73.

[8] 王颜辉,李春英.基于两种网格划分的注塑机机械手横梁的有限元分析[J].机械工程与自动化,2011(5):61-65.

[9] 李永亮,余成华,马佐成等.网格划分对边坡稳定有限元分析的影响[J].水利与建筑工程学报,2014,12(6):133-136.

[10] 何建璋,李军,伍霞.网格划分对狗骨式刚性连接非线性有限元精度和效率的影响[J].工程力学,2008,44(S1):157-160.

[11] WANG X Y,LIU H K,YU Z G.A Novel Heuristic Algorithm for IP Block Mapping onto Mesh-based Networks-on-Chip[J].The Journal of Supercomputing,2016,72 (5):2035-2058.

[12] 金丹,王巍,田大将,等.非比例载荷下缺口件疲劳寿命有限元分析[J].机械工程学报,2014,50(12):25-29.

[13] 潘城,赵光明,孟祥瑞.网格划分对爆破损伤有限元分析的影响[J].爆破,2015,32(4):21-25.

[14] 曹华军,舒林森,许磊,等.复杂机械零件的六面体有限元网格生成方法[J].机械工程学报,2014,50(15):113-118.

Abstract: ANSYS software was employed to simulate the material elastic-plastic behavior based on the previous test results under multiaxial loading.The simulations are discussed between the free mesh and mapping mesh.It shows that the calculation time of mapping mesh is 50 % of that of free mesh when there is less difference in element number and node number between the two types of meshes.The stresses at the notched root from two meshes are almost the same.The fatigue life is predicted considering the equivalent strain as the damage parameter.The predictions of mapping mesh are better than those of free mesh.The damage parameter of the notched radius 0.09 mm is conservative 3 times for free mesh.The prediction accuracies of two meshes are improved with increasing notched radius.

Keywords: notched specimen; free mesh; mapping mesh; fatigue life prediction

ApplicationofMappingGridtoFatigueLifePredictionofNotchedSpecimenunderMultiaxialLoading

SUN Ran, JIN Dan

(Shenyang University of Chemical Technology, Shenyang 110142, China)

10.3969/j.issn.2095-2198.2017.03.008

TG155.5

A

2016-07-23

国家自然科学基金项目(11102119);辽宁省自然科学基金项目(201602586)

孙然(1991-)，男，辽宁大连人，硕士研究生在读，主要从事金属材料的疲劳与断裂方面的研究.

金丹(1976-)，女，辽宁鞍山人，教授，博士，主要从事金属材料的疲劳与断裂方面的研究.

2095-2198(2017)03-0236-04