基于峰值信噪比改进的图像增强算法
2017-10-18肖祥元景文博赵海丽
肖祥元,景文博,赵海丽
(1.长春理工大学 电子信息工程学院,长春 130022;2.长春理工大学 光电工程学院,长春 130022)
基于峰值信噪比改进的图像增强算法
肖祥元1,景文博2,赵海丽1
(1.长春理工大学 电子信息工程学院,长春 130022;2.长春理工大学 光电工程学院,长春 130022)
在图像增强技术中,现有的图像增强算法在对图像进行增强时,总是伴随着原图像亮度的丢失和过度增强效果。提出一种改进的图像增强算法,该方法解决了传统图像增强过程中造成的过度增强、局部过度不自然、原始图像亮度降质的问题。实验结果证明,基于峰值信噪比的改进的图像增强方法优于现有的算法,并且该算法可以在对图像增强的基础上有效的维持原始图像的亮度。
双直方图均衡化;峰值信噪比;图像增强;最大模糊熵
在数字图像处理领域,所有传统图像增强算法都是致力于通过提高图像对比度的基础上最大程度地保持原图的亮度。图像增强算法的目的都是通过使用某个目标函数来取得一个理想的状态,在这个目标函数中图像可以获得最大清晰化视觉效果的分析状态。并且在这种状态下才可以区别于具有低对比度和技术差异的原始图像。图像增强技术被广泛应用于医学图像处理、卫星图像处理、国防科技等领域。
目前,最常用的图像增强方法大致分为两大类,即空间域增强和频率域增强,直方图均衡化是最常用的空间域增强方法之一。直方图均衡化是一种可以自行确定变换函数,并对图像进行增强的一种算法,其结果是可预知的,但缺陷是它对处理的数据不加选择,它可能会增加背景杂讯的对比度并且降低有用信号的对比度;变换后图像的灰度级减少,某些细节消失;某些图像,如直方图有高峰,经处理后对比度不自然的过度增强和原始图像亮度降质。针对这一缺陷,众多学者提出了很多其它的直方图增强改进算法,如多尺度直方图均衡化(MHE)[1]、基于亮度维持权重的聚类直方图均衡化(BPWCHE)[2]、基于动态范围分割的直方图均衡化(DRSHE)[3]、以及基于亮度维持的动态直方图均衡化(BPDHE)等技术[4]。然而上述文献中所给出的方法也仅局限于部分类型的图像,适用性并不好,而且上述方法在兼顾图像增强和图像亮度的维持上效果不够理想。针对上述问题,本文提出了一种基于峰值信噪比改进的直方图均衡化算法。该方法将最大模糊熵分割和峰值信噪比引入到直方图均衡化中,在一定程度上解决了直方图均衡化处理的对比度不自然的过分增强现象。结果表明该方法能够在图像增强的基础上有效的维持原图像的亮度,且图像增强效果优于传统的图像增强方法。
1 图像增强算法
1.1 直方图均衡化
直方图均衡化处理的中心思想是把原始图像的灰度直方图从比较集中的某个灰度区间变成在全部灰度范围内的均匀分布。直方图均衡化就是对图像进行非线性拉伸,重新分配图像像素值,使一定灰度范围内的像素数量大致相同。传统的直方图均衡化由下列概率密度函数来描述:

其中,nk表示灰度级为Xk的像素总个数。Xk和nk又是图像f的直方图上的Y轴和X轴。W是图像f的像素总个数,L是图像离散的灰度级,对于一幅位深度为8的图像,L=256。累加密度函数由下式给出:

传统的直方图均衡化方法通过累加密度函数将相应地图像映射到全部灰度级动态范围内。映射关系如下:

1.2 最大模糊熵阈值确定
由灰度级模糊理论可知,输入图像F可以被当作模糊事件。通过如下2个模糊隶属度函数将F的灰度值分为低灰度集和高灰度集两部分[5]。

其中,μd(x)为低灰度集隶属度函数,μl(x)为亮灰度集隶属度函数,a、b和c是参数,并且满足模糊集μd(x)和μl(x)发生的概率为:

其中,Px为灰度直方图,且x∈[0,255]。
低灰度集和髙灰度集的模糊熵可以由下式计算获得[6]:

从而可以得到模糊事件的总模糊熵如下:

根据模糊事件F的总模糊熵,可求得最佳模糊区间将最优阈值设为Top,根据模糊理论,当隶属度函数等于0.5时,模糊集的模糊度最高,因此,分割阈值可以用式(12)求出。

1.3 峰值信噪比与均衡化范围最优控制器
峰值信噪比这个统计学指标也被经常用来衡量图像增强的效果,峰值信噪比一个表示信号最大可能功率和影响它的表示精度的破坏性噪声功率的比值。峰值信噪比是图像失真的度量并且严重依赖于均方误差(MSE)。均方误差表达式如下[7]:

其中,f是输入图像,G是输出图像,M和N就是图像的行数和列数。

公式(14)用来计算峰值信噪比PSNR。
如果峰值信噪比的值变大,则图像的对比度增强并且在一定程度上绝对均方亮度误差减小。在本文算法中,均衡化范围最优控制器的最优范围可以通过下式求出。
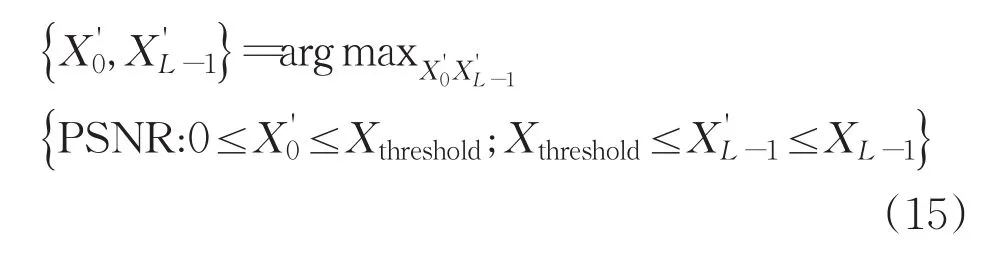
其中,Xthreshold即1.2章节中最大模糊熵对应的阈值Top。
1.4 算法描述
基于峰值信噪比改进的图像增强算法如下:
(1)阈值Top通过使用最大模糊熵来分割图像的直方图计算获得,具体计算参考1.2。
(2)计算背景部分的直方图HistB(≤Top)和前景部分的直方图HistF(>Top)。找出和HistB对应的累积密度函数CDFB,以及和HistF对应的前景累积密度函数CDFF。
(4)使用式(16)和式(17)来分别对背景部分和前景部分进行均衡化:

(5)将背景部分直方图和前景部分直方图合并作为最终输出图像

用式(18)将前景图像和背景图像合并作为最终输出图像。
2 实验结果与数据分析
为了验证本文算法优于其他现有算法,首先,采用文献[1]中的多尺度直方图均衡化(MHE)技术对图像进行处理;接着,采用文献[4]中的基于亮度维持的动态直方图均衡化(BPDHE)技术对图像进行处理;最后,采用本文算法对图像进行处理。三种算法处理的结果如图1、图2所示。
从图1中可以看出,对于多峰值输入图像,用文献[1]方法处理后的图像仍存在局部过度增强现象,如图1(c)所示,帽檐部分对比度增强过亮。用文献[4]方法处理后的图像灰度值主要集中分布在高亮范围,导致图像整体偏亮,图像对比度比较低,且原图亮度维持效果不理想,如图1(d)所示。最后采用本文方法处理后的图像,对比度明显增强,并且有效的解决了文献[1]方法处理过程中存在的局部过度增强和文献[4]方法处理后造成的图像亮度维持较差现象。从图2中可以看出,对于单峰值含噪声输入图像,用文献[1]和文献[4]算法分别对输入图像进行处理,从图2(c)、(d)可以看出处理后的图像存在大量噪声,并且都存在局部图像过度增强和对原始图像亮度维持较差的现象。而本文算法处理结果如图2(e)所示,可以看出,本文算法对单输入含噪声的图像,可以有效增强图像并维持原图像的亮度。

图1 多峰值图像处理结果对比图
由上述分析可知:与现有的图像增强算法相比,本文算法处理效果具有明显的优势。为了使上述结论更具说服力,本文从峰值信噪比(PSNR)、绝对均方亮度误差(AMBE)和信息熵3个方面对以上图像进行分析(峰值信噪比经常用来衡量图像增强的效果,峰值信噪比越大,图像增强效果越好;绝对均方亮度误差用来衡量图像亮度保持的程度,AMBE值越小图像亮度维持效果越好;模糊熵越大表示图像质量越高)。其中,绝对均方亮度误差被定义成如下形式[8]:

其中,Meanf表示输入图像的均值,MeanG是输出图像的灰度均值。

图2 单峰值图像处理结果对比图

表1 峰值信噪比值对比

表2 绝对均方亮度误差值对比

表3 信息熵值对比

图3 3种不同算法对图1处理的结果对比图

图4 3种不同算法对图2处理的结果对比图
图3和图4的横坐标表示不同的算法名称,其中MHE表示多尺度直方图均衡化算法;BPDHE表示基于亮度维持的动态直方图均衡化算法;THIS表示本文算法。纵坐标表示不同的数值,其中AMBE Value表示绝对均方亮度误差值;Entropy Value表示信息熵值;PSNR Value表示峰值信噪比值。从表1、图3和图4中的峰值信噪比值可以看出本文算法对图像的增强效果最好;同理,从表2、图3和图4中的绝对均方亮度误差值可以看出本文算法处理后的图像可以很好地保留原始图像的亮度;从表3、图3和图4中的信息熵值可以发现本文算法处理后的图像质量较高,但根本不影响本文算法对图像的增强和对原图像亮度维持的效果。综上所述,本文的算法明显优于文献[1]MHE算法和文献[4]BPDHE算法。
3 结论
针对现有的图像增强技术过程中伴随着对比度过度增强和对原始图像亮度维持差以及低对比度图像在增强的过程中伴随着噪声提高等问题,本文提出了一种基于峰值信噪比改进的图像增强算法。该算法以模糊熵为基础,用最大模糊熵将目标图像的直方图分为前景直方图和背景直方图两部分,并分别在相应的子直方图中求出取最大峰值信噪比时对应的阈值,接着分别在前景直方图和背景直方图相应地阈值区间进行直方图均衡化。最后把均衡化后的前景直方图和背景直方图合并作为最后输出图像。经过对几种算法结果的对比分析可知,本文算法不仅对图像的增强效果好,而且对原始图像亮度的维持效果也非常好。
[1]Menotti D,Najman L,Facon J.Multi histogram equalization methods for contrast enhancement and brightness preserving[J].IEEE Transactions on Consumer Electronics,2007,53(3):1186-1194.
[2]Sengee N,Choi H.Brightness preserving weight clustering histogram equalization[J].IEEE Transactions on ConsumerElectronics,2008,54(3):1329-1337.
[3]陈永亮,王华彬,陶亮.自适应动态峰值剪切直方图均衡化[J].计算机工程与应用,2015,51(1):167-171.
[4]Ibrahim H,Kong N S P.Brightness preserving dynamic histogram equalization for image contrast enhancement[J].IEEE Transactions on Consumer Electronics,2007,53(4):1752-1758.
[5]张龙涛,孙玉秋.基于模糊熵改进的直方图匹配算法研究[J].西南大学学报:自然科学版,2016,38(4):124-129.
[6]马超玉.光照不均匀条件下图像增强算法研究[D].长春:长春理工大学,2014.
[7]陈驰.光学相关图像增强技术研究[D].长春:长春理工大学,2012.
[8]刘春香.基于DSP图像增强系统的设计与实现[D].长春:长春理工大学,2010.
An Improved Image Enhancement Algorithm Based on the Peak-Signal to Noise Ratio
XIAO Xiangyuan1,JING Wenbo2,ZHAO Haili1
(1.School of Electronics and Information Engineering,Changchun University of Science and Technology,Changchun 130022;2.School of Optoelectronic Engineering,Changchun University of Science and Technology,Changchun 130022)
In the image enhancement technology,the existing image enhancement algorithm is always accompanied by the loss of the original image brightness and excessive enhancement effect when the image is enhanced.Therefore,an improved image enhancement algorithm is proposed,which solves the problem that the traditional image enhancement process is over-enhanced,the local over-unnatural,the original image brightness is degraded.The experimental results show that the improved image enhancement method based on peak signal to noise ratio is superior to the existing algorithm,and the algorithm can effectively maintain the brightness of the original image on the basis of image enhancement.
bi-histogram equalization;PSNR;image enhancement;the maximum fuzzy entropy
TP751.1
A
1672-9870(2017)04-0083-04
2017-04-28
肖祥元(1992-),男,硕士研究生,E-mail:1779764587@qq.com
景文博(1980-),男,博士,副教授,E-mail:wenbojing@sina.
