基于改进蚁狮算法的电力系统最优潮流计算
2017-10-18靳保源童煜栋严敬汝
栗 然, 张 凡, 靳保源, 范 航, 童煜栋, 严敬汝
(新能源电力系统国家重点实验室(华北电力大学),河北 保定 071003)
基于改进蚁狮算法的电力系统最优潮流计算
栗 然, 张 凡, 靳保源, 范 航, 童煜栋, 严敬汝
(新能源电力系统国家重点实验室(华北电力大学),河北 保定 071003)
电力系统的最优潮流计算问题是一个多维、非线性的优化问题。它通过调节发电机有功出力、机端电压等控制变量来达到优化系统的某一性能指标的目的,并保证所有的约束条件都得到满足。基于蚁狮优化算法搜索能力强大而利用能力不足的特点,提出一种改进蚁狮优化算法(MALO)来求解电力系统的最优潮流问题。改进算法通过在建模中引入漩涡收敛方式,在增强原算法利用能力的同时,也更加符合蚁狮捕食蚂蚁的生物学机制。以发电机成本和全网网损为目标函数,将改进算法用于阿尔及利亚电网及标准IEEE30节点的最优潮流计算中,并与原算法和其它一些智能算法进行比较,验证了改进算法的优越性。该改进算法对于实际电力系统的规划和运行具有一定的参考意义。
电力系统; 最优潮流; 改进蚁狮算法
0 引言
2015年国网实现售电量34 506亿kW·h,对应的全网线损率为6.78%,而同期发达国家如德国的网损率只有4%左右。我国的网损率与发达国家有着较大差距,电力系统的节能降损尚有巨大潜力。且我国用电量巨大,降损0.1个百分点即可产生几十亿元的经济效益。而最优潮流计算作为实现电力系统的经济运行的有效手段,受到了广泛关注。
最优潮流的概念最早由Carpentier于20世纪60年代提出[1-2]。其主要目的是通过调节可利用的控制变量如发电机输出功率、可调变压器抽头等来寻找能满足所有运行约束条件的,使系统的某一性能指标(如发电成本或网络损耗)达到最优值下的潮流分布。早期电力系统的最优潮流主要通过经典的数学规划方法来求解,例如梯度法、线性规划法、非线性规划法、二次规划法、内点法以及牛顿法等[3-8]。但经典方法对起始点比较敏感,且要求目标函数可导,限制了其在大规模非线性优化问题中的应用。为了克服这些缺点,遗传算法(GA)、粒子群算法(PSO)、差分算法(DE)[9-14]等进化类算法相继被用来解决电力系统的优化问题, 并不断提升着最优潮流计算的性能。这类算法与导数无关,无需进行假设和近似,具有一定随机性,能跳出局部最优点,且具有内在并行性,能处理非连续、非光滑及高度非线性解空间的复杂优化问题,展现了良好的收敛特性和寻优能力。然而最优潮流本质上是一个NPC问题,除非遍历控制变量的可行域(由于有些控制变量连续可调,这不可能实现),否则无法给出一个绝对最好的优化方案。因此,如何提高算法的性能,在满足各运行约束条件的前提下找到使得某一目标函数更优的解,一直是广大学者和研究人员不断探索的问题。
蚁狮优化算法(The Ant Lion Optimizer, ALO)是澳大利亚学者Seyedali Mirjalili受到自然界蚁狮捕猎蚂蚁行为的启发于2014年提出的一种新型元启发式算法[15-16],包括单目标和多目标两个版本。且已经在一些工程领域如三杆桁架、悬臂梁和齿轮传动的设计上得到了应用。但ALO算法在迭代寻优过程中,蚁狮种群存在适应度相对较差的个体,如果蚂蚁选定该蚁狮进行游走可能会降低搜寻效率。另外,蚂蚁随机游走的过程虽然保证了搜索(Exploration)能力,却降低了对已找到的最优解充分利用(Exploitation)的能力,这都在一定程度上影响了ALO算法的寻优性能和收敛效率。
基于此,本文提出一种改进蚁狮优化算法(MALO)来求解电力系统的最优潮流问题。改进算法通过在建模中引入漩涡收敛方式,在增强原算法利用能力的同时,也更加符合蚁狮捕食蚂蚁的生物学机制。以发电机成本和全网网损为目标函数,将改进算法用于阿尔及利亚电网和IEEE30节点系统的最优潮流计算中,并与原算法和其它一些智能算法进行比较,验证了改进算法的优越性。该改进算法对于实际电力系统的规划和运行具有一定的参考意义。
1 最优潮流模型
电力系统最优潮流是一个多变量、非线性和多约束的组合优化问题[10]。数学上可表示为:
minf(x,y)
(1)
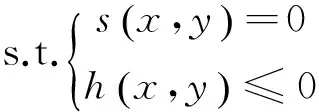
(2)
式中:x是控制变量,通常包括发电机有功出力、机端电压、变压器变比和无功补偿容量;y为状态变量,包括PQ节点电压、发电机无功出力等;f是目标函数,如发电费用,全网网损等;s是节点潮流方程等式约束;h为各不等式约束,如发电功率约束、电压幅值约束等。
1.1状态变量和控制变量
该模型的控制变量包括:
xT=[PG2…PGNG,VG1…VGNG,QC1…QCNC,T1…TNT]
式中:PG为除发电机1(作为平衡节点)之外所有发电机节点的有功输出;VG为所有发电机节点的机端电压;QC为并联电容补偿容量;T为变压器分接头位置;NG、NC和NT分别为发电机节点数,并联电容补偿器数以及变压器分接头数。
状态变量包括:
yT=[PG1,VB1…VBNB,SL1…SLNL]
式中:PG1为平衡节点的有功输出;VB为各负荷节点的电压;SL为各条线路流过的功率;NB、NL分别为PQ节点数和线路数。
1.2约束条件
1.2.1 等式约束
最优潮流是经过优化的潮流分布,必须满足基本潮流方程。其等式约束条件为:
(3)
式中:N为节点总数;PGi为节点i的有功输出;QGi为节点i的无功输出;PDi为节点i的有功负荷;QDi为节点i的无功负荷;Vi和Vj分别为节点i和j的电压;Gij和Bij分别为节点i和j之间的电导和电纳。
1.2.2 不等式约束
(1)发电机约束:
(4)
(5)
(6)
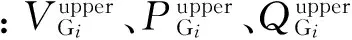
(2)变压器约束:
(7)
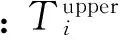
(3)并联电容补偿器约束:
(8)
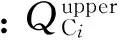
(4)安全约束:
(9)
(10)
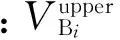
本文通过牛顿-拉夫逊法进行潮流计算,得到所有状态变量的值,并采用罚函数方程来处理状态变量的不等式约束问题。表示如下:
(11)
(12)
(13)
(14)
式中:PF为平衡节点有功出力越限的罚函数项;QF为发电机节点无功出力越限的罚函数项;VF为节点电压越限的罚函数项;ηP、ηQ、ηV分别为对应惩罚项的罚系数。
1.3目标函数
为了考察新算法的性能,本文使用发电机成本以及有功网损两项指标作为目标函数。
1.3.1 发电成本最小
发电机的发电/燃料成本可表示为:
(15)
式中:ri为发电机i的发电(燃料)成本;αi、βi和γi为发电机i的成本系数。
1.3.2 全网网损最小
系统总网损为所有节点发出的有功功率减去所有节点的有功负荷,即:
(16)
式中:各变量含义如(1.2.1)节所述。
1.3.3 多目标优化问题
相比单目标的优化问题,实际电力系统更多的需要进行多目标之间的权衡以求得多个优化目标的非劣解集,或帕累托(Pareto)最优解。本文使用上述两个目标函数求取其帕累托最优解,以验证改进算法在处理多目标优化问题上的性能。
2 改进蚁狮优化算法
2.1原始的蚁狮算法
蚁狮算法模拟的是自然界中蚁狮(幼虫)捕猎蚂蚁的行为。蚁狮在捕食前会用其巨大的下颚挖出一个锥形的陷阱,并藏在陷阱底部等待蚂蚁(当然也包括其它一些小昆虫)到来,在蚁狮周围随机游走的蚂蚁可能落入其中。蚂蚁一旦落入陷阱后会拼命试图逃脱,这时蚁狮会向陷阱边缘抛沙以使蚂蚁再次滑落并将其捕食。随后蚁狮会重新构造陷阱以准备进行下一次捕猎。
2.1.1 蚂蚁的随机游走
蚂蚁的随机游走过程即视作各搜索代理搜寻可行域的过程。数学上可表示为:
X(t)=[0,cumsum(2r(t1)-1),…,
cumsum(2r(tk)-1)]
(17)
式中:X(t)为蚂蚁的随机游走步数集;cumsum表示计算累加和;k为随机游走的步数(本文取为最大迭代次数);而r(t)为一个随机函数,定义为:
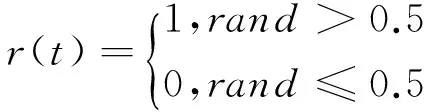
(18)
式中:rand为[0,1]上均匀分布的随机数。图1模拟了蚂蚁的三次随机游走过程(k取50),可以看出随机游走过程有较强的搜索能力。
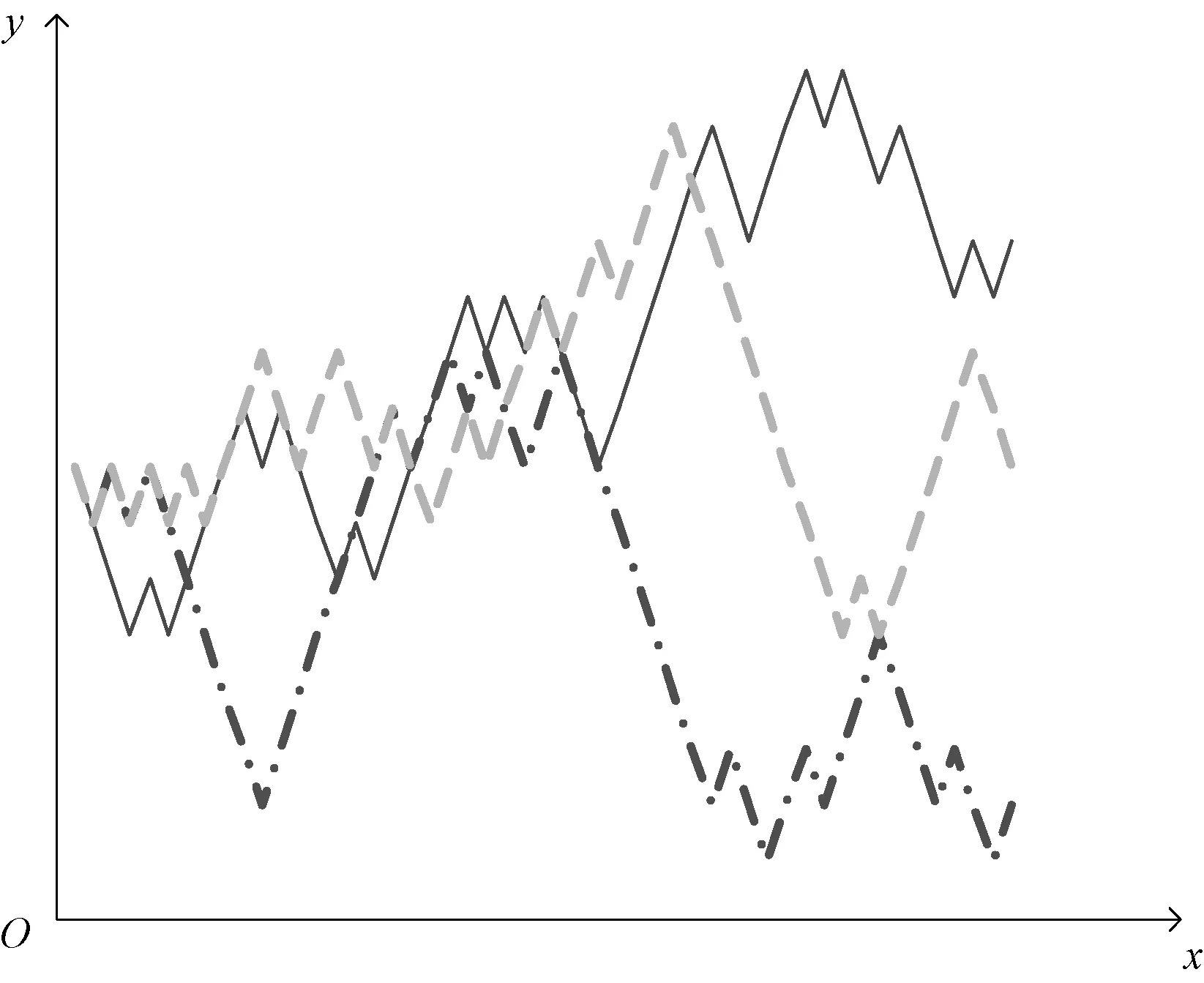
图1 蚂蚁的三次随机游走过程
为了保证蚂蚁随机游走在可行域的范围内,不能只根据式(17)更新蚂蚁的位置,还要根据式(19)进行归一化:
(19)
2.1.2 蚁狮对蚂蚁的影响
蚂蚁在随机游走过程中其行动会受到蚁狮陷阱的影响,数学上表示为:
(20)
(21)
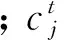
2.1.3 蚁狮的捕食过程
每只蚂蚁只能被一只蚁狮捕获,某只蚂蚁具体要被哪只蚁狮捕获是通过轮盘赌(Roulette Wheel)策略来选择的,适应度越高的蚁狮有着更高的捕获蚂蚁的机会。另外,蚁狮可以构造陷阱,蚂蚁一旦落入陷阱,蚁狮就会向外扬沙以使蚂蚁不至于逃脱,这时蚂蚁随机游走的范围将急剧缩小。数学上表示为:
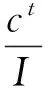
(22)
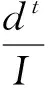
(23)
(24)
式中:I是比例系数;T为最大迭代次数;w为一随迭代次数增大的数(本文取0.1T
当某只蚂蚁的适应度变得高于蚁狮时,即认为其被蚁狮捕获,此时蚁狮会根据蚂蚁的位置来更新其位置,表示为:
(25)
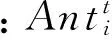
2.1.4 精英策略
每一次迭代获得的适应度最好的蚁狮被认为是精英蚁狮。精英蚁狮将影响所有蚂蚁的行动。第t只蚂蚁在第t+1代的位置由下式确定:
(26)
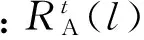
2.2蚁狮算法改进
由上述介绍可以看出,蚁狮算法对可行域的搜索很大程度上是通过蚂蚁在蚁狮附近的随机游走实现的。而随机游走有着较大的发散性,即该算法的搜索能力是有保证的,但缺乏对最优解的充分利用。另外,原算法在模拟蚁狮俘获蚂蚁的过程时不够具体,只是简单地令蚁狮根据式(25)更新自己的位置。因此本文对蚁狮算法作出两点改进。
2.2.1 漩涡状收敛
为了增强算法的利用能力,同时也更好的模拟蚂蚁落入蚁狮陷阱的场景,改进算法使蚂蚁在困入蚁狮的陷阱时以漩涡状的方式滑向等待在陷阱中心的蚁狮,引入阿基米德螺线[17](如图2)来模拟这一过程,令蚂蚁的位置通过下式更新:
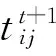
(27)
(28)
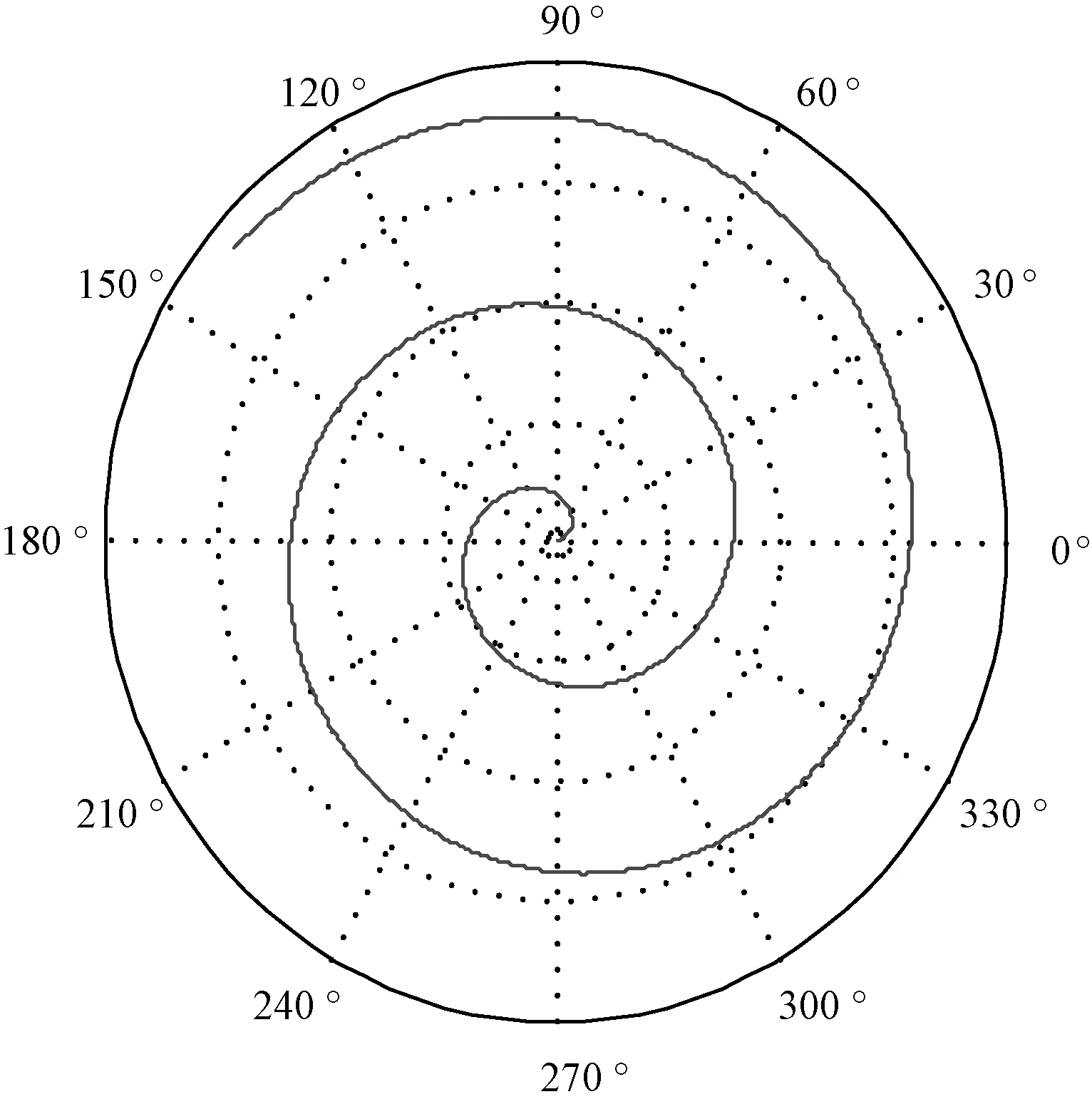
图2 阿基米德螺线
2.2.2 蚂蚁的行走过程
蚂蚁在每一代中有可能能够以式(26)的方式自由的随机游走,也有可能以式(27)的方式滑向蚁狮的陷阱中心。为了平衡两者,本文采用如下策略:
(1)每一代中蚂蚁以概率p进行随机游走(考虑到实际情况,p一般取为0.6~0.8,本文取0.7)。
(2)每一代中蚂蚁有1-p的可能性被蚁狮俘获,一旦被俘获,它将在以后的n代失去随机游走的能力,并以阿基米德螺线的形式不断地滑向等待在陷阱中心的蚁狮(n可以取最大迭代次数的1/10到1/50,本文将n取为最大迭代次数的1/25)。此时要再作出判断,因为蚂蚁有p1的概率被一只(通过轮盘赌选出的)普通蚁狮俘获,也有可能以1-p1的概率被精英蚁狮俘获,本文取p1为0.5。
如此改进一方面更好的模拟了蚁狮捕食蚂蚁的生物学行为,另一方面通过蚂蚁滑向蚁狮陷阱的过程增强了算法的利用能力,实现了蚁狮算法在搜索和利用上的平衡。
2.3改进蚁狮算法步骤
综上所述,改进后的蚁狮算法步骤如下:
(1)确定蚂蚁和蚁狮的规模及维数,在可行域内随机初始化蚂蚁和蚁狮的位置,并计算蚂蚁和蚁狮的适应度值。
(2)取蚁狮种群中适应度最好的的一只蚁狮作为精英蚁狮。
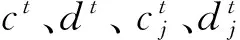
(4)每一代后重新计算蚂蚁和蚁狮的适应度值,取适应度值前50%的位置作为新一代蚁狮的位置,取适应度值最好的位置为新的精英蚁狮的位置。
(5)判断是否到达最大迭代次数,如果达到则输出结果并结束迭代, 否则重复第(3)步。
3 算例分析
3.1单目标优化问题
单目标优化问题所用算例为阿尔及利亚电网系统,其主网架为220 kV,共有59个节点。包括10台发电机、83条线路以及36个负荷节点(总负荷684.10 MW)。其网络拓扑结构图及具体参数见文献[18,19],此处不再列出。所用控制变量共18个:包括8台发电机的有功出力和10台发电机的机端电压,如下表1所示。为简单起见,认为所有控制变量连续可调。
设置算法迭代次数为500,蚂蚁与蚁狮的规模均为50。潮流计算方法为牛顿-拉夫逊法。与本文算法作比较的算法为原始蚁狮优化算法(ALO),结果取两种算法独立运行20次的平均值。其他一些算法的优化结果已有文献研究[17-23],本文不再进行仿真,直接列出结果。
值得一提的是,该算例中1号发电机为平衡机,其有功输出为状态变量,只能调节机端电压。5号发电机(节点编号13)故障不能出力,但可以调节机端电压。其它8台发电机均可正常调节。
另外,阿尔及利亚电网结构较为复杂,控制变量选择不当容易出现病态潮流(潮流不收敛),本文将病态潮流时的目标函数值取为无穷大。
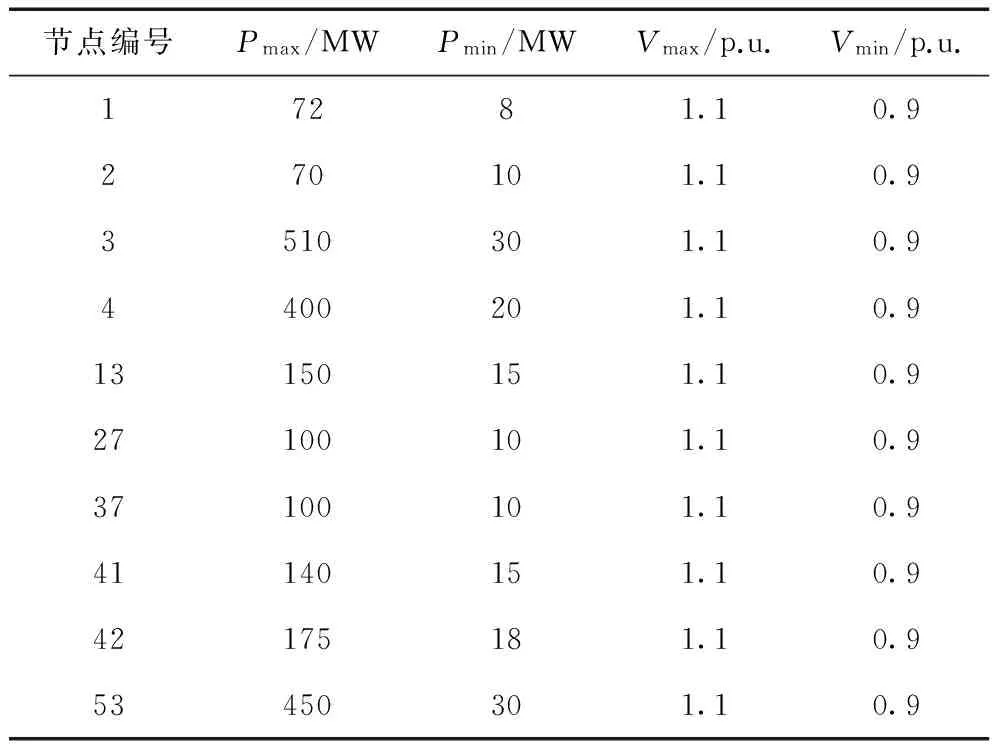
表1 阿尔及利亚电网各发电机参数
3.1.1 场景1——燃料成本
原算法与改进算法的的燃料成本优化过程如图3所示。
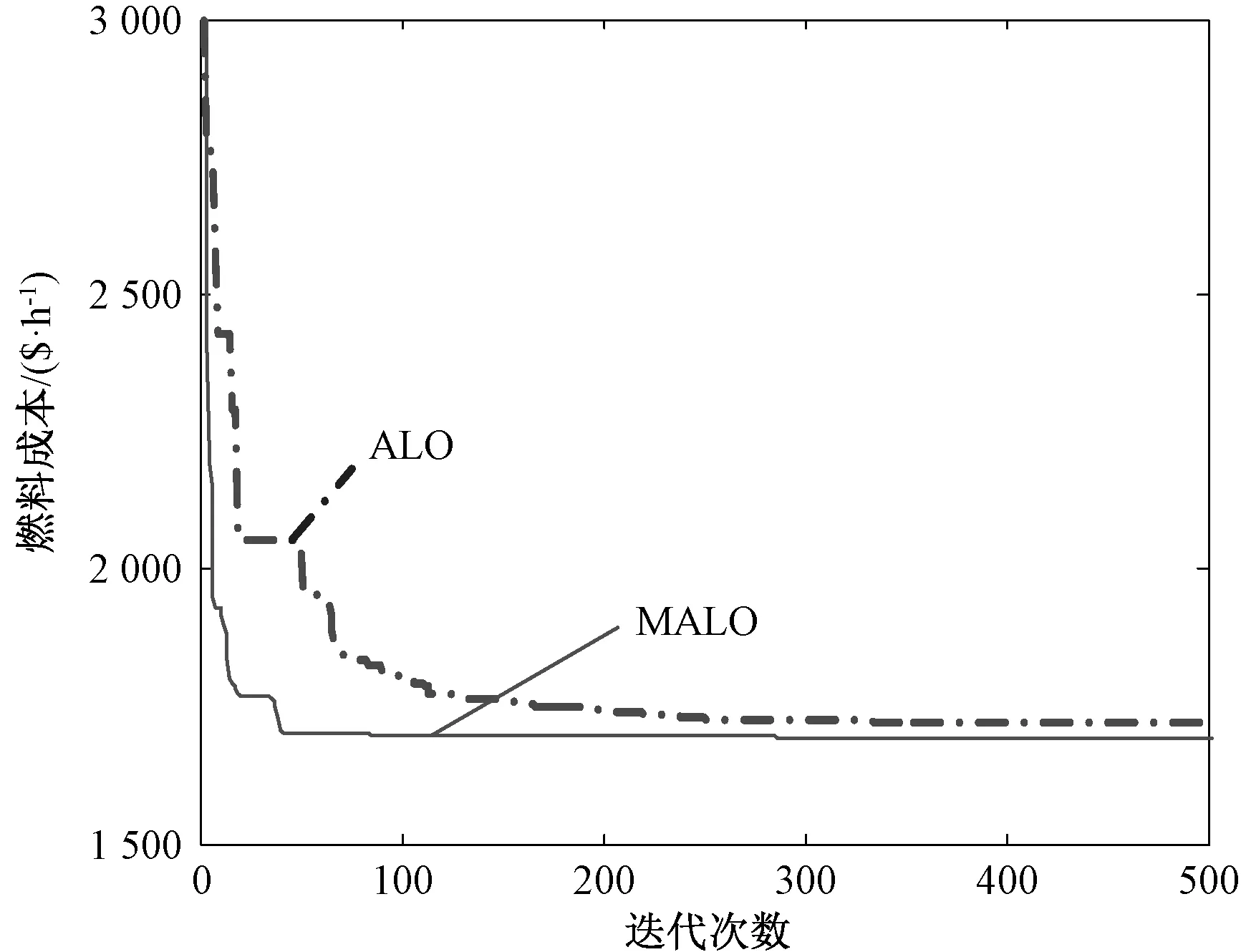
图3 燃料成本的优化过程对比
由上图可见,改进蚁狮算法由于较好的平衡了搜索和利用的程度,在未丧失后期寻优能力的前提下使得算法的收敛速度得到了大幅的提高。MALO与其他算法的详细对比如表2所示。
另外,阿尔及利亚电网的初始燃料成本为 1 943.70$/h,本文所提改进算法可降低成本13.05%。
3.1.2 场景2——全网网损
图4即为原算法与改进算法的有功网损优化过程。
表3为两种算法的对比。
阿尔及利亚电网初始网损为29.14 MW,本文方法可实现降损接近一半(49.04%)。
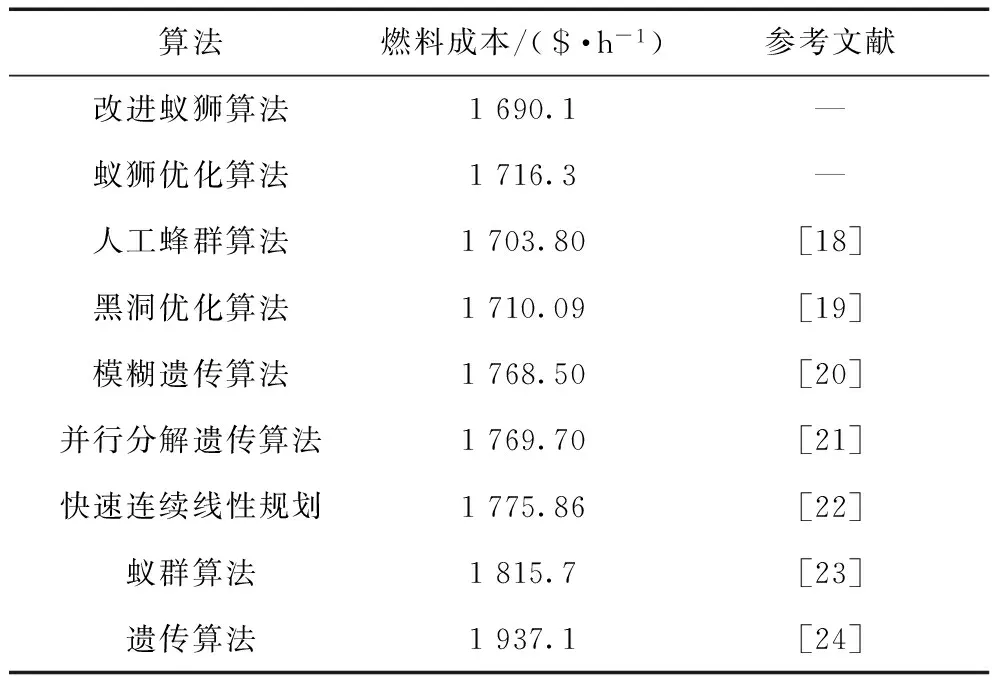
表2 场景1下不同算法比较
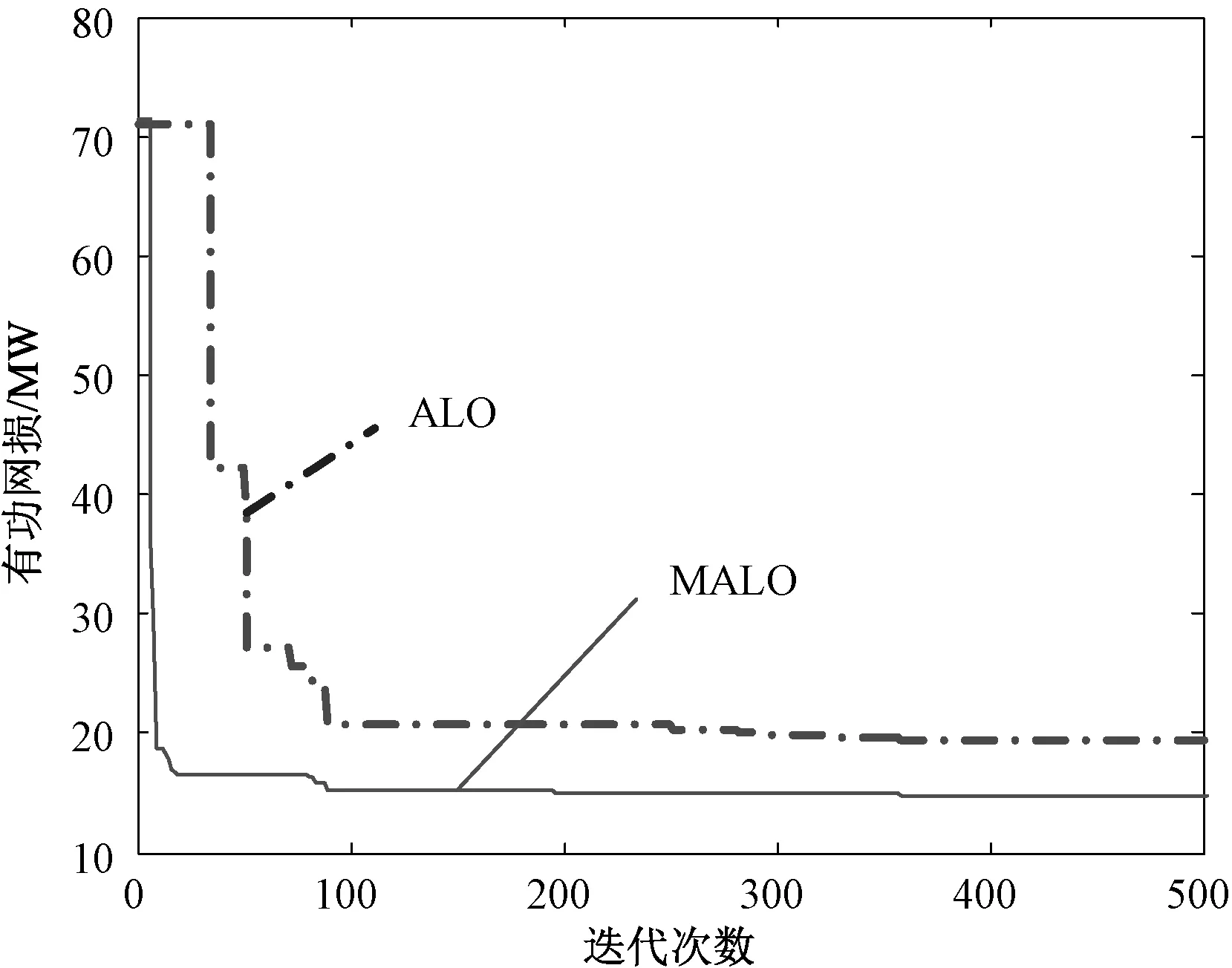
图4 有功网损的优化过程对比
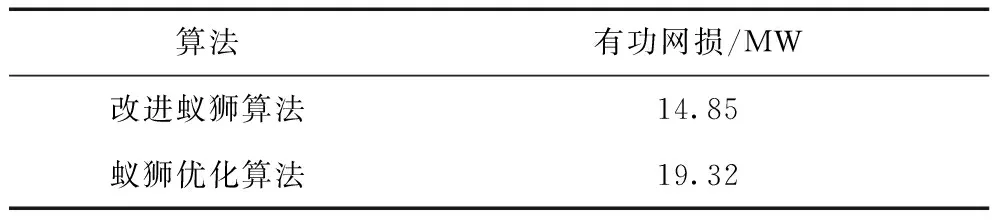
算法有功网损/MW改进蚁狮算法14.85蚁狮优化算法19.32
注:文献[17-23]均未考虑场景2。此处不再列出。
另外,阿尔及利亚电网在初始状态、场景1及场景2下的控制变量值略。
3.2多目标优化问题
将MALO嵌入原始蚁狮算法的多目标版本(MOALO)[16],即蚂蚁的学习方式如前所述,但不改变非支配集的维护策略,形成改进算法的多目标版本(MMOALO)。多目标优化问题所用算例为标准IEEE30节点系统,共有6台发电机、4台变压器、41条线路以及两个并联电容器。所用控制变量共24个:包括5台发电机的有功出力、6台发电机的机端电压、4台变压器的变比及9个并联电容补偿器(分别设在节点10,12, 15,20,21,23,24和29)。为简单起见,认为所有控制变量连续可调。IEEE30节点系统结构图、参数、控制变量及状态变量的上下限约束见文献[11,14]。此处不再列出。
多目标优化问题设置迭代次数、种群规模以及存档大小皆为100。与改进算法做对比的算法包括原始多目标蚁狮算法(MOALO)以及多目标粒子群算法(MOPSO)[24-25],各算法参数见对应文献。取各算法独立运行20次的平均值。不同算法获得的帕累托前端如下图5所示。
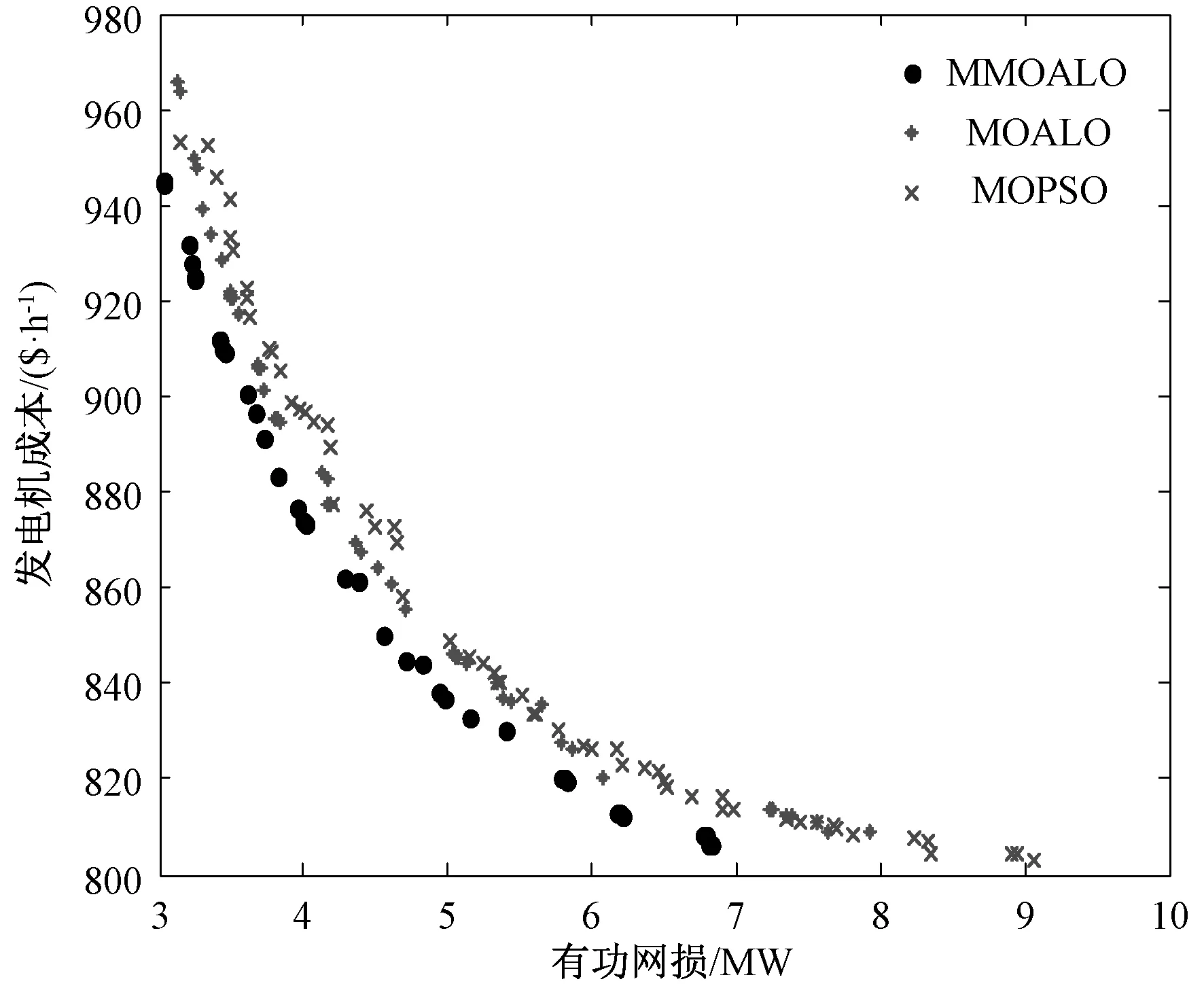
图5 不同算法获得的Pareto前端
由上图可以直观地看出相比其他3种算法,MMOALO获得了更优的帕累托前沿,发电成本和全网网损目标函数值最靠近坐标轴。另外,为了定量的评价改进算法的效果,本文使用C指标[26]来做进一步分析。C指标可用于描述两个解集之间的支配关系,对于两个解集Q1和Q1,其计算公式为
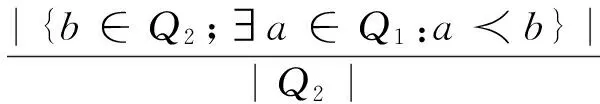
(29)
式中:C(Q1,Q2)为Q1关于Q2的C指标,可衡量Q2中有多大比例的解被Q1中的解支配。例如C(Q1,Q2)=0.6表示Q2中有60%的解被Q1中的解支配。
各算法C指标中位数如下表4所示。
由上表可见MMOALO相对于MOALO、MOPSO解集的C指标中位数分别为0.990 0和 0.932 2,反之则为0和0,说明MMOALO在处理多目标优化问题上具有明显优势。其它算法的优劣顺序依次为MOALO、MOPSO。
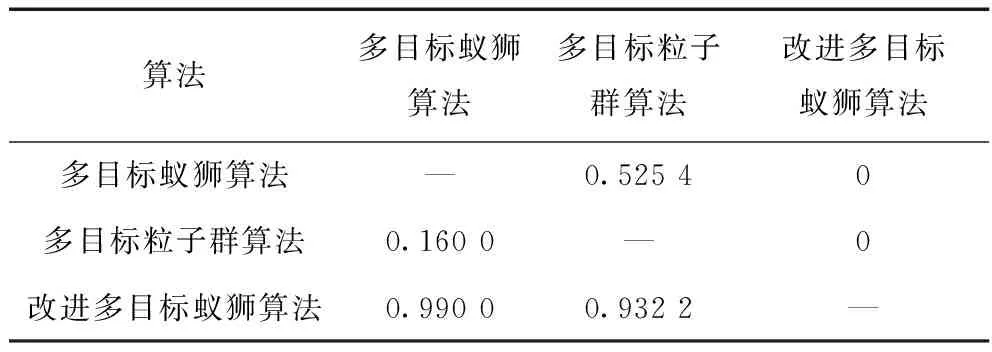
表4 不同算法C指标中位数
4 结论
本文基于蚁狮优化算法搜索能力强大而利用能力不足的特点,提出了一种改进蚁狮优化算法(MALO)来求解电力系统的最优潮流问题。改进算法通过在建模中引入漩涡收敛方式,在增强原算法利用能力的同时,也更加符合蚁狮捕食蚂蚁的生物学机制。以发电机成本和全网网损为两个目标函数,将改进算法用于阿尔及利亚电网及标准IEEE30节点的最优潮流计算中,并与原算法和其它一些智能算法进行比较,验证了改进算法的优越性。该改进算法对于实际电力系统的规划和运行具有一定的参考意义。
另外,改进算法在考虑蚂蚁被蚁狮俘获的过程中根据实际情况使得它可能被普通蚁狮俘获,也可能被精英蚁狮俘获。但为简单起见,可以假设蚂蚁只会被精英蚁狮俘获,因为这一改进本质上是为了增强算法的利用能力。经过实际仿真亦发现这两种机制的效果是类似的。
最后,MMOALO虽具有更好的支配性能,但其Pareto解集分布的均匀度欠佳,进一步改进以提高其解的均匀度是下一步需要研究的问题。
[1] CARPENTIER J. Contribution à l'étude du dispatching économique [C]// Bull. Soc. Francaise D'Electricité. 1962.
[2]DOMMEL H W, TINNEY W F. Optimal power flow solutions[J]. IEEE Transactions on Power Apparatus & Sys-tems, 1968, PAS-87(10):1866-1876.
[3]LEE K Y, PARK Y M, ORTIZ J L. A united approach to optimal real and reactive power dispatch[J]. IEEE Transactions on Power Apparatus & Systems, 1985, 5(5):1147-1153.
[4]MOTAPALOMINO R, QUINTANA V H. Sparse reactive power scheduling by a penalty function-linear programming technique[J]. IEEE Transactions on Power Systems, 1986, 1(3):31-39.
[5]HABIBOLLAHZADEH H, LUO GX, SEMLYEN A. Hydrothermal optimal power flow based on a combined linear and nonlinear programming methodology[J]. IEEE Power Engineering Review, 1989, 9(5):51-52.
[6]BURCHETT R C, HAPP H H, VIERATH D R. Quadratically convergent optimal power flow[J]. IEEE Transactions on Power Apparatus & Systems, 1984, 103(11):3267-3275.
[7]杨利水, 杨旭, 顾家翠. 原-对偶内点法和预测-校正内点法在最优潮流的应用[J]. 华北电力大学学报(自然科学版), 2012, 39(6):29-34.
[8]SUN D I, ASHLEY B, BREWER B, et al. Optimal power flow by newton approach[J]. IEEE Transactions on Power Apparatus & Systems, 1984, 103(10):2864-2880.
[9]刘先正, 温家良, 潘艳,等. 采用改进粒子群算法的直流电网最优潮流控制[J]. 电网技术, 2017, 41(3):715-720.
[10]LAI L L, MA J T, YOKOYAMA R, et al. Improved genetic algorithms for optimal power flow under both normal and contingent operation states[J]. International Journal of Electrical Power & Energy Systems, 1997, 19(5):287-292.
[11]ABIDO M A. Optimal power flow using particle swarm optimization [J]. Middle East Journal of Scientific Research, 2002, 24(7):563-571.
[12]林昭华, 侯云鹤, 熊信艮,等. 广义蚁群算法用于电力系统无功优化[J]. 华北电力大学学报(自然科学版), 2003, 30(2):6-9.
[13]MOHAMED A A A, MOHAMED Y S, EL-GAAFARY A A M, et al. Optimal power flow using moth swarm algorithm[J]. Electric Power Systems Research, 2017, 142(9):190-206.
[14]ELA AAAE, ABIDO M A, SPEA S R. Optimal power flow using differential evolution algorithm[J]. Electrical Engineering, 2009, 91(2):878-885.
[15]MIRJALILI S. The ant lion optimizer[J]. Advances in Engineering Software, 2015, 83(6):80-98.
[16]MIRJALILI S, JANGIR P, SAREMI S. Multi-objective ant lion optimizer: a multi-objective optimization algorithm for solving engineering problems[J]. Applied Intelligence, 2017,46(1):79-95.
[17]王明华, 杨继绪. 阿基米德螺线的性质与应用[J]. 数学通报, 1989(7):11-12.
[18]SLIMANI L, BOUKTIR T. Economic power dispatch of power systems with pollution control using artificial bee colony optimization[J]. Turkish Journal of Electrical Engineering & Computer Sciences, 2013, 21(21):1515-1527.
[19]BOUCHEKARA H R E H. Optimal power flow using black-hole-based optimization approach[J]. Applied Soft Computing, 2014, 24(11):879-888.
[20]MAHDAD B, BOUKTIR T, SRAIRI K. Optimal power flow of the algerian network using genetic algorithm/fuzzy rules[C]// IEEE Power and Energy Society General Meeting - Conversion and Delivery of Electrical Energy in the Century, 2008:1-8.
[21]MAHDAD B, BOUKTIR T, SRAIRI K. OPF with envi-ronmental constraints with SVC controller using decomposed parallel GA: Application to the Algerian network[C]// IEEE Power & Energy Society General Meeting, 2009:1-8.
[22]ZEHAR K, SAYAH S. Optimal power flow with environmental constraint using a fast successive linear programming algorithm: application to the algerian power system[J]. Energy Conversion & Management, 2008, 49(11):3362-3366.
[23]RODDER D, LOTTERS S. Optimal power flow of the algerian electrical network using an ant colony optimi-zation method[J]. Leonardo Journal of Sciences, 2005, 18(7):43-57.
[24]BOUKTIR T, SLIMANI L. Optimal power flow of the algerian network using genetic algorithms[J]. Wseas Transactions on Circuits & Systems, 2004, 6(6):1-5.
[25]COELLO C A C, PULIDO G T, LECHUGA M S. Handling multiple objectives with particle swarm optimization[J]. IEEE Transactions on Evolutionary Computation, 2004, 8(3):256-279.
[26]李鸿鑫, 李银红, 陈金富,等. 自适应选择进化算法的多目标无功优化方法[J]. 中国电机工程学报, 2013, 33(10):71-78.
Optimal Power Flow Using Modified Ant Lion Optimizer
LI Ran, ZHANG Fan, JIN Baoyuan, FAN Hang, TONG Yudong, YAN Jingru
(State Key Laboratory of Alternate Electrical Power System with Renewable Energy Sources,North China Electric Power University,Baoding 071003,China)
The calculation of the optimal power flow (OPF) in power system is a multi-dimensional and nonlinear problem, which tries to optimize the performance of the power system by adjusting the control variables such as active output and terminal voltage of generation units within all constraints. A modified ant lion optimizer (MALO) is proposed in this paper to solve the optimal power flow in power system based on the characteristics of powerful exploration and poor exploitation of the original algorithm. The vortex convergence method, which enhances the exploitation of original algorithm and makes it more accordant with the biological mechanism of ant lion's hunting behavior, is introduced into the modeling of MALO. Then, the modified algorithm is applied to the optimal power flow calculation in Algerian electrical network and IEEE 30-bus system which takes the generator cost and the whole network loss as two objective functions. Superiority of MALO is verified by comparing the results with ALO and some other intelligent algorithms. The modified algorithm will have a certain reference value for planning and operating of the practical power system.
power system; optimal power flow; modified ant lion optimizer
10.3969/j.ISSN.1672-0792.2017.09.003
TM 744
A
1672-0792(2017)09-0015-08
2017-05-16。
广东电网有限责任公司电力调度控制中心科技项目(036000QQ00150002)。
栗然(1965-),女,博士,教授,主要研究方向为交直流电网优化降损,电力系统分析、运行与控制;张凡(1993-),男,硕士研究生,主要研究方向为交直流电网优化降损,电力系统分析、运行与控制;靳保源 (1992-),男,硕士研究生,主要研究方向为电力系统分析、运行与控制;范航(1993-),男,硕士研究生,主要研究方向为电力系统分析、运行与控制;童煜栋 (1992-),男,硕士研究生,主要研究方向为电力系统风险评估;严敬汝 (1993-),女,硕士研究生,主要研究方向为电力系统分析、运行与控制。
