应用于输电线路故障测距的行波波速仿真分析

曾志明，凌志勇，，袁宜真，谷湘文

（1. 湖南工业大学 电气与信息工程学院，湖南 株洲 412007；2. 国家电网湖南省电力公司株洲供电公司，湖南 株洲 412011；3. 广东电网肇庆怀集供电局，广东 怀集 526499）

应用于输电线路故障测距的行波波速仿真分析

曾志明1，凌志勇1，2，袁宜真3，谷湘文2

（1. 湖南工业大学 电气与信息工程学院，湖南 株洲 412007；2. 国家电网湖南省电力公司株洲供电公司，湖南 株洲 412011；3. 广东电网肇庆怀集供电局，广东 怀集 526499）

基于输电线路故障时产生的暂态行波进行故障定位，既能满足超高压输电线路对保护装置迅速动作的速度要求，还能对故障进行精确定位，且基本不受故障类型的影响。影响行波故障测距精度的主要因素有行波的速度和行波波头准确到达时刻的标定。针对常用的行波波速确定方法——公式法和在线测量法，通过在不同线路长度、不同故障距离下的仿真分析得到相对应的行波波速，并将所得到的波速用于同一故障距离测量，通过对测距结果对比分析，找出在某种故障距离下的最优波速，从而达到提高测距精度的效果。通过仿真分析发现，在线实时测量波速在合适范围内的测距精度比固定波速的测距精度高，满足规范标准对测距误差不超过1%的要求。

输电线路；故障测距；暂态行波；行波波速

0 引言

当输电线路发生故障后，快速、准确地找到故障点，对提高供电可靠性具有重要意义。输电线路故障定位技术的发展可以分为3个阶段，即人工巡线阶段、阻抗法阶段和暂态行波测距阶段[1]。对于输电线路故障的定位，最初采用人工巡线方式，但是以该方式定位输电线路故障不仅耗费的人力和物力较大，而且效率十分低下。随着输电电压等级的不断提高和输送容量的不断增大，继电保护装置的快速动作对提高系统的稳定性具有重要意义，人工巡线方式已经不再适用，因此开始采用阻抗法和暂态行波测距方式。以阻抗法定位输电线路故障时，由于其理论的局限性，故障测距结果容易受到过渡电阻的影响[5]。而以暂态行波法定位输电线路故障时，测距结果基本不受故障类型的影响，因此在输电线路上使用具有一定的优势[8-9]。但是暂态行波在线路正常运行时不存在，只有在线路故障或者开关分合闸时才会产生，并且行波的传播速度会受到线路参数的影响。可见，只有精确测量行波的波速和行波波头的到达时间才能获得精确的故障距离，因此，研究行波波速对于提高测距精度具有重要意义[7]。

依据A、B、C、D、E、F型行波将行波故障测距装置分为6种基本类型。其中，A、B、E、F型行波测距装置采用单端原理，而C、D型行波测距装置采用双端原理[1]。目前，行波测距中的A型和D型行波测距装置已在我国高压和超高压交直流输电线路上大量应用，该装置的使用明显提高了故障测距精度，取得了显著的社会效益和巨大的经济效益[2]。行波测距装置通常采用固定的整定波速作为故障测距中的计算波速，但是因输电线路的距离增加，线路参数易受到地理、气候、天气等的影响而导致其发生微小变化，进而影响行波的线路传播速度。可见，采用固定的整定波速会导致测距精度下降，而采用行波速度在线测量可以实时修正行波的传播速度，提高故障测距的精度。因此，本研究拟对影响测距精度主要因素之一的行波速度进行仿真研究，对D型行波测距装置行波波速在线测量的适用性进行全面的仿真分析，以期为输电线路故障的快速定位提供一定的理论参考。

1 D型行波故障测距原理

D型行波故障测距利用故障暂态行波的双端测距原理，它利用线路内部故障产生的初始行波浪涌达线路两端测量点的绝对时间之差值计算故障点到两端测量点之间的距离[1]。

图1所示为D型行波测距原理示意图。

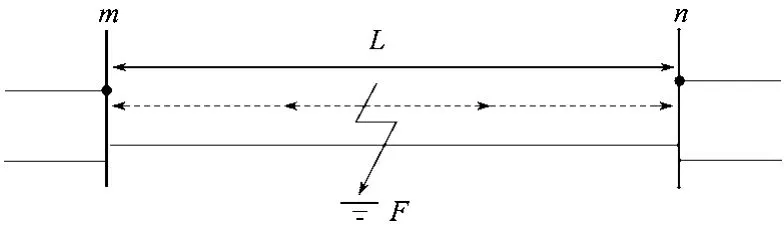
图1 D型行波测距原理示意图Fig. 1 Schematic diagram of D-type traveling wave distance measurement

设故障线路长度为L，m和n为线路的两个端点，F为故障点，其距离m端的距离为L1，距离n端的距离为L2，设故障初始行波浪涌以相同的传播速度v进行传播，行波到达m端和n端母线的时间分别为tm和tn，则存在如下关系：

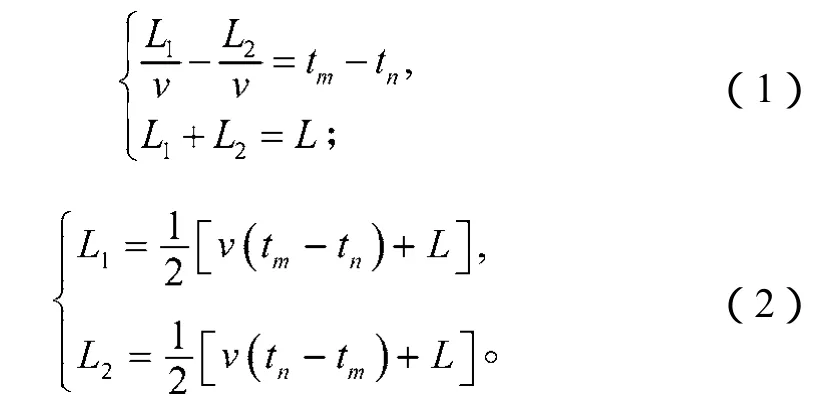
通过公式（1）和（2）就能计算出输电线路中故障点与线路端点间的距离。

2 小波变换

小波变换是近20多年来兴起的一种新的信号分析处理技术，它是针对传统的傅里叶分析与其后的短时傅里叶分析的不足而提出来的。小波是有效延伸范围有限且可伸缩的衰减振荡函数，小波变换的本质是计算被分析信号波形与小波波形的局部相似程度，也就是分析信号在不同位置处的特点不同的局部行为，这正是故障测距所需进行的工作，所以小波变换在故障测距中得到了广泛的应用[2]。

能称为小波的函数都具有如下3个基本性质：

1）能作为一般函数的结构单元；

2）有时-频分辨能力；

3）有相应的快速变换算法。

通过对一个母函数Ψ(t)作伸缩、平移变换，生成一个函数族{Ψb,a(t)}，以使小波获得随变化的时-频分辨能力。

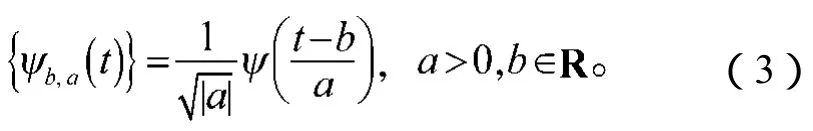
式中：a和b分别为尺度因子和平移因子；

Ψ为一个样本函数，它具有时-频分辨能力，即对于某一正数ε＞0，它应满足式（4）所示要求。

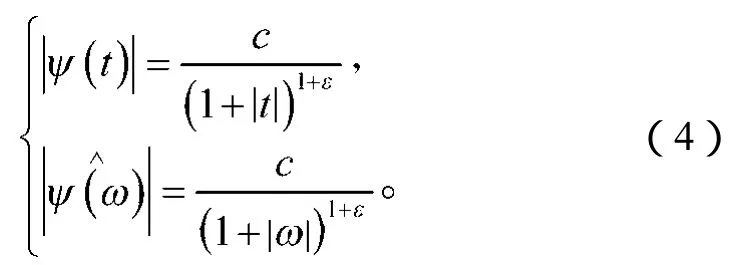
式中：c为常数，且0＜c＜∞；

若母函数Ψ(t)称作母小波，则函数族{Ψb,a(t)}统称为小波。

当要求小波能分解与重建L2(R)空间的函数时，L2(R)代表平方可积空间，母小波需满足以下最基本的条件：

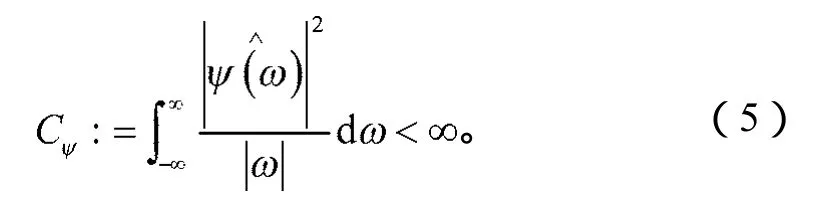
式中：“:=”是“定义为”之意，即定义CΨ代表右边所示的积分；

ω为角频率。

小波变换具有良好的时频局部化特性，能够同时从时域和频域描述奇异信号的每个细节，是一种时间窗和频率窗都可以根据信号的具体形态来动态调整的信号分析方法[4]。该时频局部化分析方法为：在低频部分采用较高的频率分辨率和较低的时间分辨率；在高频部分采用较高的时间分辨率和较低的频率分辨率。这一特点决定了小波变换对信号的奇异点非常敏感，适用于时变非平稳信号的检测与分析[6]。

小波种类繁多，包括基本小波、连续小波、二进小波、小波框架、Riesz小波、正交小波、半正交小波、双正交小波等，不同小波分别适合于不同用途[1]。对于具体的问题，需依据其特征并结合各小波的特性找到合适的小波，且应选择合适尺度以达到理想的效果。因此，选择合适的小波和合适的分析尺度是成功应用小波变换的关键之一。

3 行波波速的计算方法

3.1 公式计算方法

当输电线路的长度和电磁波的波长相比不能忽略时，不能采用集中参数模型，而必须使用分布参数模型[3]。由于线路具有分布的电阻、电感、电导、电容，会导致导线上产生波过程，如果是集中参数，则无波过程。

在输电线路上发生故障产生行波时，由于采用三相输电方式，各相之间存在相互耦合的现象，使分析计算困难。因此，通常采用坐标变换将相空间变为其它坐标空间，如可将三相导线时的参数解耦等效为与单导线时相同，即将相空间变换为模空间，这个空间的电压、电流称为模电压、模电流。工程实际中，通常将模量分为地模分量和线模分量。当不考虑线路的损耗和频率特性时，输电线路的线模分量和地模分量的速度计算公式分别为：

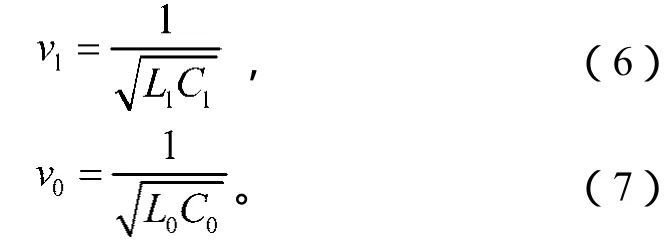
式（6）（7）中：

L1和L0分别为单位长度的正序电感和零序电感；

C1和C0分别为单位长度的正序电容和零序电容。

由于地模分量存在着较大的衰减和随频率变化大等问题，这会导致行波损耗大且波速不稳定，对故障定位的精度有较大影响。线模的波速在不考虑线路依频特性时，速度相对稳定，可以依据线路参数计算出其近似值。因此，当系统三相对称短路故障时，通常选取α、β作为分析对象：当系统发生两相接地短路和相间短路、以非故障相为相模变换基准相时，应选取β模为分析对象，将不会与0模和α模发生模混叠现象；当系统发生单相接地短路时，各模量之间均存在模量混叠现象，但是当以故障相为基准相时，虽然α模只和0模发生混叠，仍然可以选取α模作为分析对象[3-4]。

3.2 在线实时测量方法

本文选用双端行波测距装置，当在保护区外发生故障时，利用本身行波检测装置来进行行波波速测量[10-12]。发生区外故障时，线路两端的行波检测装置能够灵敏地启动，记录电压、电流的行波数据，无需给出故障测距结果，但应能用于测量行波的实时波速。设输电线路保护范围的距离为L，其为母线m和n二者保护装置安装之间的距离。当区外故障时，产生的暂态行波将通过保护线路的全长，故障初始行波到达本侧和对侧母线的时刻分别为t1,t2，则行波波速为

4 行波波速确定方案研究

由公式（6）计算得出的固定波速，是在假定输电线路为无损线路的前提下得到的，即不考虑线路的损耗和频率特性，但实际输电线路通常情况下是有损耗的，且暂态行波一般为高频分量，是有频率特性的。因此，由该公式计算得到的波速与线路的实际波速值会有一定的偏差。

由公式（8）计算得到的波速，在输电线路本身较长和区外故障发生在较远处时，由于行波衰减畸变，导致检测到的到达两侧的时间不准确，甚至存在较大的误差，此时计算的行波波速将存在较大误差。

在传统出版向知识服务时代的转型中，国外一些大型出版企业走在了前列，可以为国内专业出版行业的转型提供参考。

在本方案设计中，将在输电线路距离不同、区外故障发生位置不同等条件下，进行行波波速的仿真计算。线路的参数，比如单位长度的电阻、电感、电容，都在线路建设好之后就已确定给出，所以通常由公式（6）计算出来的波速将会是一个固定值，且其未考虑线路参数随运行方式改变和气候条件变化等带来的影响，故将其作为基本参考波速。由公式（8）计算得到的波速是一个实时量，它将随线路参数和运行方式等的变化而变化，因此将其作为实时测量波速。将测量波速与故障测距装置设置的整定波速进行故障测距的仿真分析，并通过对测距结果进行对比分析，找出最优波速。

5 输电线路仿真分析

5.1 仿真步骤

1）确定仿真模型参数

本研究在电磁暂态仿真软件PSCAD/EMTDC(power systems computer aided design/ electro magnetic transient in DC system)中建立仿真模型，图2所示为其示意图。

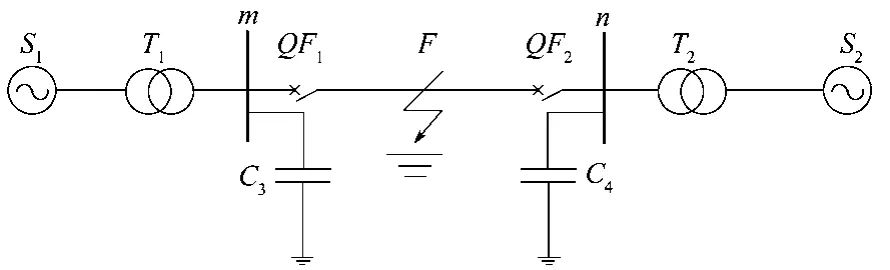
图2 系统仿真模型Fig. 2 System simulation model

在本系统仿真模型中，电压等级为500 kV双电源系统，母线m、n采用集中分布式线路模型等效，其单位长度（以1 km计）正序、负序和零序的电阻、电感、电容分别如下：

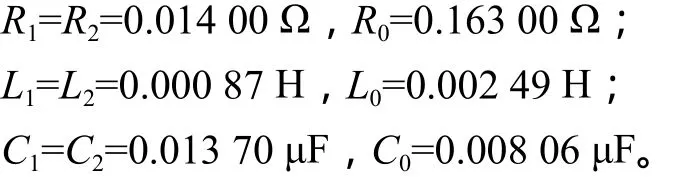
C3,C4为母线等效杂散电容，且C3=C4=1×10-8F。

根据以上给出的线路参数，利用公式（6）计算得到的线路固定波速v1=2.896 54×108m/s。设线路故障发生于0.100 s整时刻，用于故障分析的波形数据是截取于0.095 999～0.108 001 s之间的故障波形，采样频率为1 MHz。

2）测量故障点确定的实时波速

设定在保护线路区外40 km处发生故障，母线长度分别为60, 180, 300, 600 km，由公式（8）对行波波速进行实时测量，得到该线路的实时波速，所得结果见表1，其中v=L/(t1-t2)。

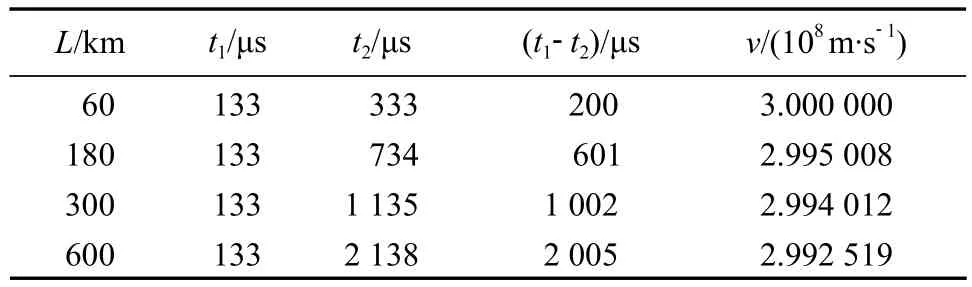
表1 不同母线长度下区外40 km处发生故障时的波速测量结果Table 1 Wave velocity measurement results at the time of failure occurring at 40 km outside the zone under different bus lengths

3）测量母线长度确定的实时波速

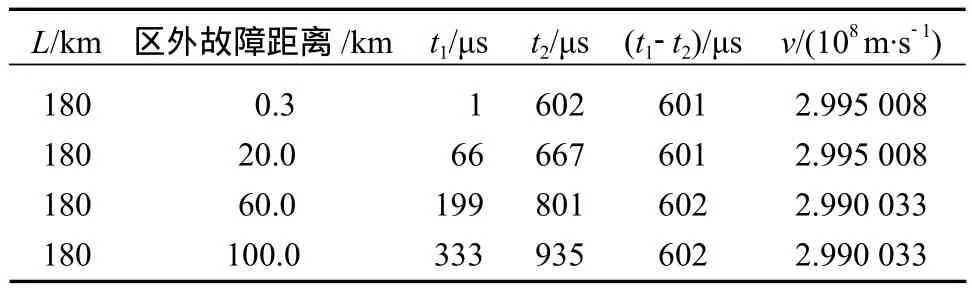
表2 母线长180 km时不同区外故障位置的波速测量结果Table 2 Wave velocity measurement results at the time of failure occurring at 180 km

4）测量故障点、母线长度不确定的实时波速

在长度不同的母线线路上任意位置处发生故障时，母线m和n端的行波检测装置记录下故障产生的电压暂态行波。并对m和n端的电压行波进行Karrenbauer变换，以消除三相线路相间耦合。

5）确定初始行波到达时刻

将PSCAD中Karrenbauer变换后的波形导入MATLAB中进行小波变换，由小波变换的模极大值确定两端初始行波到达的准确时刻。

6）计算故障距离

由小波变换得到的初始行波波头准确到达时刻，确定整定波速和实时测量波速，由公式（1）和（2）算出故障发生的距离。

对比分析表1和表2中的数据可以得知，当区外故障距离增加或输电线路长度增加时，由公式（8）测量到的波速均减小。这是因为：由于线路长度的增加，暂态行波中的高频分量在传播过程中会发生较大程度的衰减，而暂态行波的波速和频率成正比例关系，频率越高，速度越快；但是高频具有的能量较少，容易衰减，由于行波衰减畸变导致的到达两侧的时间不准确，存在一定的误差。

图3～5依次为m侧母线行波装置检测到的初始电压行波、m侧初始电压行波经相模变换后的波形和m侧小波变换模极大值。

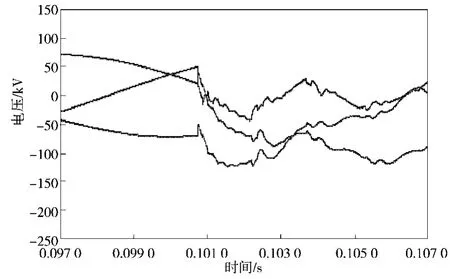
图3 m侧三相初始电压行波Fig. 3 m-side three-phase initial voltage traveling waves

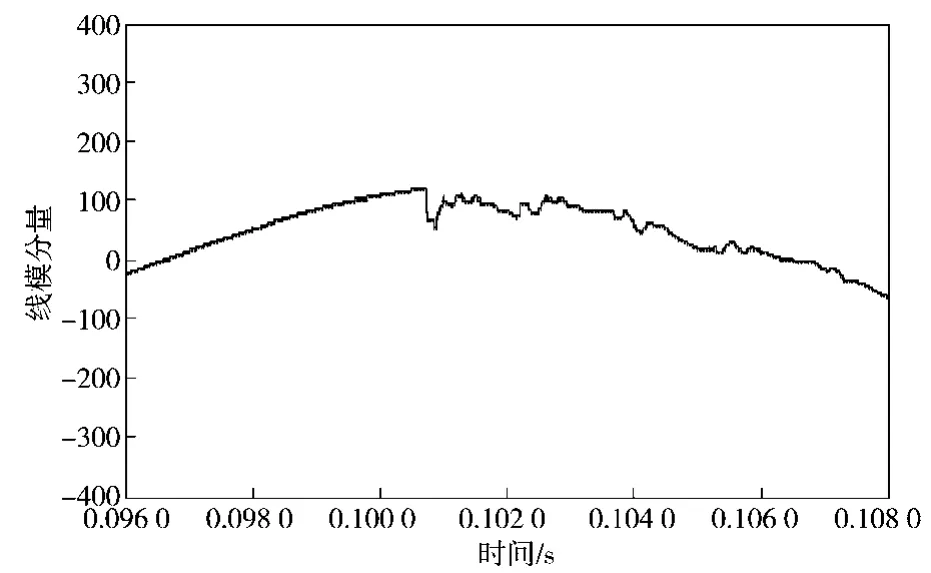
图4 m侧相模变换后波形Fig.4 m-side phase mode transformation waveform

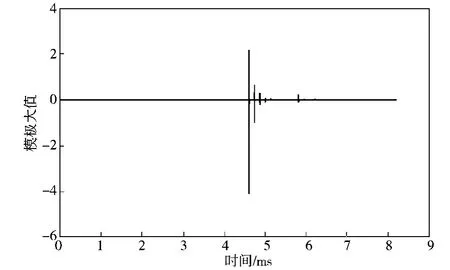
图5 m侧小波变换模极大值Fig. 5 Modulus maxima of m-side wavelet transform

首先，在PSCAD/EMTDC中进行输电线路故障仿真，得到三相初始行波电压，为消除相间耦合对测量结果的影响，对其进行相模变换，等效为一相的测量结果；再将其导入MATLAB中进行小波变换，然后由小波变换的模极大值确定m侧初始电压行波的准确到达时刻。

图6～8依次为n侧母线行波装置检测到的初始电压行波、n侧初始电压行波经相模变换后的波形和n侧小波变换模极大值，数据处理方法同前。

图3～8的图形均为输电线路长度为180 km，故障发生在距离m端40 km处时的波形图，限于文章篇幅，只列出上述图形，其它线路长度和线路故障位置处理过程与其一致。

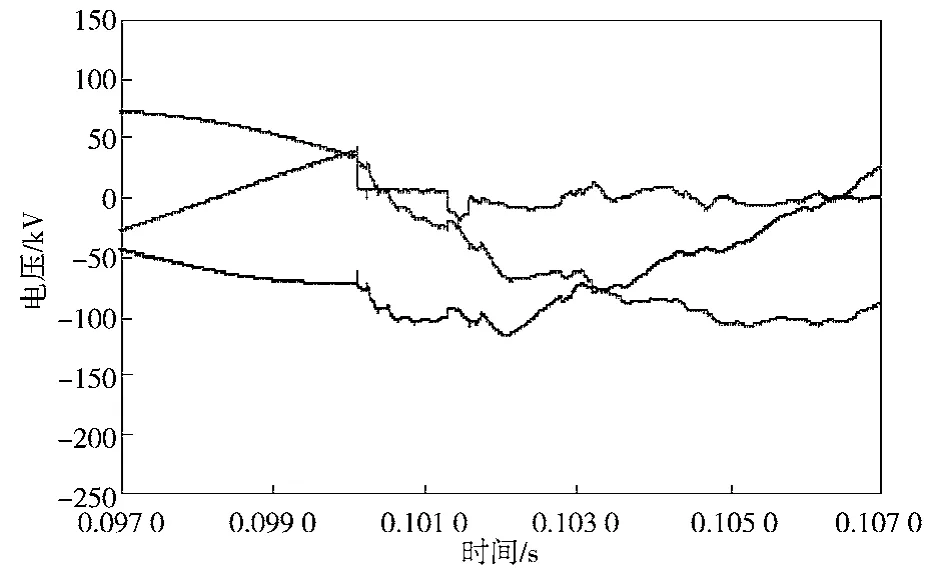
图6 n侧初始电压行波Fig. 6 n-side initial voltage traveling wave

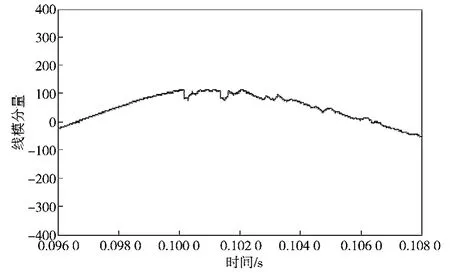
图7 n侧相模变换后波形Fig. 7 n-side phasic transformation waveform

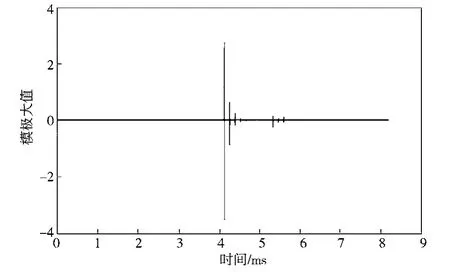
图8 n侧小波变换后波形Fig. 8 n-side wavelet transform waveform

5.2 故障测距结果和数据分析

不同的线路长度、故障位置处A相接地故障的定位结果如表3所示。其中，表中固定波速测距结果为由公式（6）根据线路参数算得的行波速度，测量波速测距结果为区外40 km处发生故障时，实际测得的行波速度。

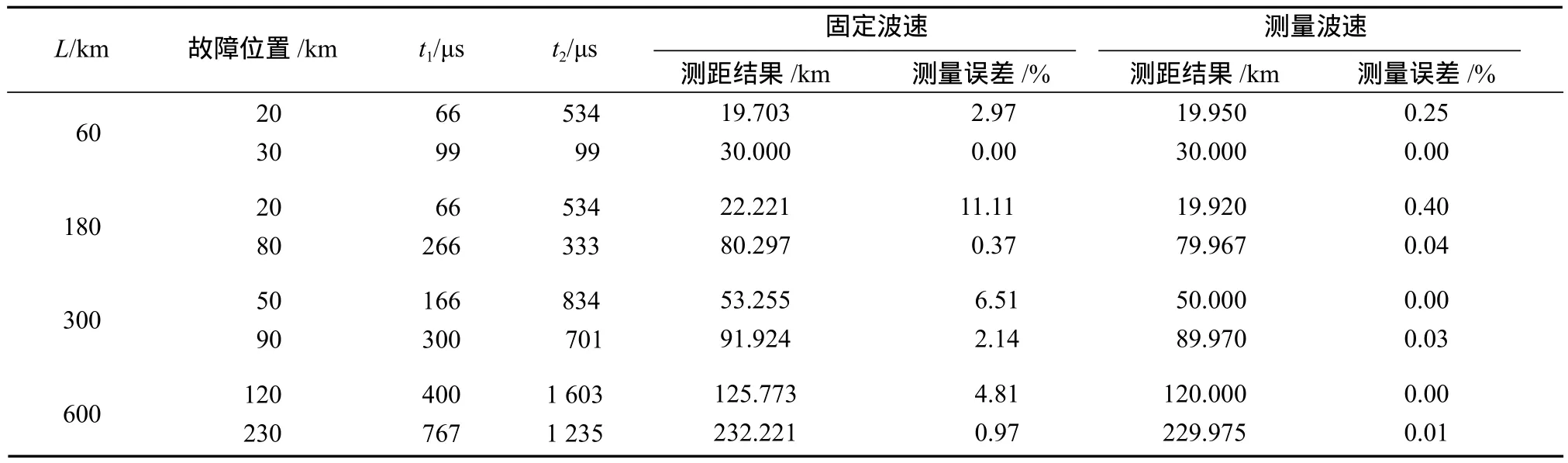
表3 不同线路长度和故障位置A相接地故障定位结果Table 3 Results of A phase ground fault location at different line lengths and different fault locations

本研究设置线路中点故障，并且求出了初始行波到达的时间和测距结果，可以为线路其它故障距离测定提供参考，由表3可以简单地判断初始行波到达时间与测距结果是否有效。对比表3中的固定波速测距结果和测量波速测距结果可知：测量波速的测距结果比固定波速的测距结果更加准确，当线路长度在60～600 km之间增加时，测量波速的测距误差都在规范标准不超过1%的误差范围内。

由表1可知，当线路长度变化时，测量波速也发生变化，当线路长度较短时，测量得到的波速较大，甚至超越了光速，产生了误差。这主要是因为暂态行波为高频量，传播速度非常接近光速，而传播距离较短，高频量衰减也比较少。本文采用的行波采样频率为1 MHz，时间精确到1 μs，在时间上存在细微的误差，但由表3的故障测距结果可知，该误差在误差允许范围之内，因而测距结果有效。当线路长度增加时，波速呈缓慢下降的变化趋势，这是因为由于线路长度的增加，高频量比低频量更容易衰减，而行波的传播速度和频率成正比，所以虽然测量波速下降，但仍然满足测距精度要求。

对比表3中的固定波速测距结果和测量波速的测距结果可知：采用公式（6）的计算波速只有在很小的一段距离上能满足测距精度要求，其适用范围具有较大的局限性；而由公式（8）测量计算得到的波速，不管是在线路本身较长或较短、区外故障发生在较远处时，均能满足测距精度要求。

6 结论

为了提高暂态行波故障测距的精度，本文对影响测距精度主要因素之一的行波速度进行了仿真研究，对行波波速在线测量的适用性进行了较为全面的仿真分析，可得出如下结论：

1）行波波速测量方法，在输电线路故障定位中测量误差较小，不管是长线路还是短线路，均能满足误差要求，适用范围较广。而由线路参数计算得到的固定波速，在输电线路故障测距应用中具有局限性，只在一定的线路长度范围内能满足测距精度要求。因此，在实际应用中需谨慎选用，但可以作为行波波速的大概估算用。

2）分析行波波速测量结果（见表1）和测距结果（见表3）可知，行波波速在2.990 000 00×108m/s到光速c=2.997 924 58×108m/s之间，故障测距结果误差均能满足误差精度要求，这对于行波波速整定具有一定的指导意义。

3）本文只考虑了输电线路单相接地故障时的情形，行波波速测量法均能满足要求，其它故障类型理论上亦能适用，但仿真验证还需进一步分析。

[1]葛耀中. 新型继电保护和故障测距的原理与技术[M].2版.西安：西安交通大学出版社，2007：181-332.GE Yaozhong. Principle and Technology of New Relay Protection and Fault Location[M]. 2nd ed. Xi’an：Xi’an Jiaotong University Press，2007：181-332.

[2]覃 剑，陈祥训，雷林绪. 输电线路行波故障测距技术及小波变换应用[M]. 北京：中国电力出版社，2014：20-120.QIN Jian，CHEN Xiangxun，LEI Linxu. Transmission Line Traveling Wave Fault Location Technology and Wavelet Transform Application[M]. Beijing：China Electric Power Press，2014：20-120.

[3]黄 雄，王志华，尹项根，等. 高压输电线路行波测距的行波波速确定方法[J]. 电网技术，2004，20(19)：34-36.HUANG Xiong，WANG Zhihua，YIN Xianggen，et al.Travelling Wave Velocity Measurement in Fault Location Based on Travelling Wave for High Voltage Transmission Line[J]. Power System Technology，2004，20 (19)：34-36.

[4]覃 剑，陈祥训，郑健超，等. 利用小波变换的双端行波测距新方法[J].中国电机工程学报，2000,20(8)： 6-10.QIN Jian，CHEN Xiangxun，ZHENG Jianchao，et al. A New Double Terminal Method of Travelling Wave Fault Location Using Wavelet Transform[J]. Proceedings of the CSEE，2000，20(8)：6-10.

[5]姜 博，董新洲，施慎行. 基于单相电流行波的配电线路单相接地故障选线方法[J].中国电机工程学报，2014，34(34)：6216-6227.JIANG Bo，DONG Xinzhou，SHI Shenxing. A Method of Single Phase to Ground Fault Feeder Selection Based on Single Phase Current Traveling Wave for Distribution Lines[J]. Proceeding of the CSEE，2014，34(34)：6216-6227.

[6]董杏丽，葛耀中，董新洲，等. 基于小波变换的行波测距式距离保护原理的研究[J].电网技术，2001，25(7)： 9-13.DONG Xingli，GE Yaozhong，DONG Xinzhou，et al.Wavelet Transform Based Distance Protection Scheme with Travelling Wave Fault Location[J]. Power System Technology，2001，25(7)：9-13.

[7]曾祥君，尹项根，林福昌，等. 基于行波传感器的输电线路故障定位方法研究[J]. 中国电机工程学报，2002，22(6)：42-46.ZENG Xiangjun，YIN Xianggen，LIN Fuchang，et al. Study on Fault Location for Transmission Line Based on the Sensor of Travelling-Wave[J]. Proceedings of the CSEE，2002，22(6)：42-46.

[8]陈学伟.500 kV输电线路精确故障定位技术研究[D].济南：山东大学，2013.CHEN Xuewei. Research on Accurate Fault Location Technology for 500 kV Transmission Lines[D]. Jinan：Shandong University，2013.

[9]CROSSLEY P A，MCLAREN P G. Distance Protection Based on Travelling Waves[J]. IEEE Transactions on Power Apparatus and Systems，1983，PAS-102(9)：2971-2983.

[10]董新洲，王 珺，施慎行. 配电线路单相接地行波保护的原理与算法[J].中国电机工程学报，2013，33(10)：154-160.DONG Xinzhou，WANG Jun，SHI Shenxing. Principle and Algorithm of Traveling Waves Based Single-Phase-to-Ground Protection for Distribution Lines[J].Proceedings of the CSEE，2013，33(10)：154-160.

[11]DONG Xinzhou，WANG Jun，SHI Shenxing，et al. Traveling Wave Based Single-Phase-to-Ground Protection Method for Power Distribution System[J].CSEE Journal of Power and Energy Systems，2015，1(2)：75-82.

[12]王 珺，董新洲，施慎行. 配电线路单相接地行波保护的实现与试验[J]. 中国电机工程学报，2013，33(13)：172-178.WANG Jun，DONG Xinzhou，SHI Shenxing. Scheme and Test of Traveling-Waves Based Single-Phase-to-Ground Protection for Distribution Lines[J]. Proceedings of the CSEE，2013，33(13)：172-178.

（责任编辑：廖友媛）

A Simulation Analysis of Traveling Wave Velocity for Fault Location of Transmission Lines

ZENG Zhiming1，LING Zhiyong1，2，YUAN Yizhen3，GU Xiangwen2
（1. School of Electrical and Information Engineering，Hunan University of Technology，Zhuzhou Hunan 412007，China；2. State Grid Zhuzhou Power Supply Company，Zhuzhou Hunan 412011，China；3. Guangdong Power Grid Zhaoqing Huaiji Power Supply Bureau，Huaiji Guangdong 526499，China）

Based on the transient traveling wave generated by the fault of the transmission line, which can meet the requirement in terms of speed for high speed transmission lines in quick response to the protective devices, and can achieve an accurate location of the faults without being affected by the fault type. The main factors in fl uencing the accuracy of traveling wave fault are the speed of traveling wave and the calibration of the arrival time of the traveling wave heads. In view of the commonly used methods for determining the wave speed of lines：formula method and online measurement method, the corresponding traveling wave velocity can be obtained by simulation analysis at different line lengths and different fault distances. The obtained wave velocity is used for the same fault distance measurement. A comparison and analysis made of the ranging results helps to determine the optimal wave velocity at some fault distance, thus improving its ranging accuracy. A simulation analysis shows that the accuracy of the on-line real-time measurement of the wave velocity is higher than that of the fi xed wave velocity in appropriate ranges, which meets the requirement of the standard deviation within 1%.

transmission line；fault location；transient traveling wave；traveling wave velocity

TM452

A

1673-9833(2017)04-0032-07

10.3969/j.issn.1673-9833.2017.04.006

2017-03-10

湖南省研究生科研创新基金资助项目（CX2017B684）

曾志明（1992-），男，湖南耒阳人，湖南工业大学硕士生，主要研究方向为电力系统继电保护，E-mail：337914923@qq.com

凌志勇（1967-），男，湖南株洲人，湖南工业大学高级工程师，主要从事电力生产技术管理工作，E-mail：1959573787@qq.com