正交面齿轮数控磨削齿面误差修正研究
2017-10-18方曙光明兴祖王红阳
方曙光,明兴祖,王红阳,罗 旦
(湖南工业大学 机械工程学院,湖南 株洲 412007)
正交面齿轮数控磨削齿面误差修正研究
方曙光,明兴祖,王红阳,罗 旦
(湖南工业大学 机械工程学院,湖南 株洲 412007)
首先,基于面齿轮的啮合原理和数控磨削展成坐标系之间的变换关系,建立了面齿轮的齿面数学模型,并对面齿轮齿面进行5×9网格划分和节点坐标理论值计算;然后,采用三坐标测量机测出了磨削齿面节点的坐标测量值,通过对齿面误差的分析和分解,得到了齿面网格节点处的齿面偏差值;最后,建立了齿面误差的识别方程,并提出采用序列二次规划方法,对机床加工参数进行优化求解,从而完成了对面齿轮齿面误差的修正。齿面误差修正结果表明,齿面工作区域部分的齿面误差总体趋于平稳,即修正后的齿面误差得到了明显的改善,但是靠近齿面的过渡区域还需要进一步完善。
面齿轮;齿面误差;三坐标测量;磨削参数;序列二次规划
1 研究背景
面齿轮传动是一种圆柱齿轮与圆锥齿轮啮合的齿轮传动方式,它具有结构紧凑、重合度大、传动平稳等优势[1-2]。磨削作为面齿轮的最后一道加工工序,以形成面齿轮的最终齿面几何形状、微观形貌和表层性态,其优劣决定了面齿轮的使用性能和寿命。但是综观已有研究,对于磨削后面齿轮的精度(如齿面的几何精度等)要求,目前还无统一的标准。
1)国外已有研究
国外对于面齿轮制造技术方面的研究相对于国内该方面的研究起步较早,且国外已有研究中常采用齿轮测量仪对面齿轮的齿面偏差进行测量,以评判面齿轮的精度。
F. L. Litvin等人[3]较早地提出了面齿轮磨削加工理论,并且建立了面齿轮磨削加工机构。
G. Goch[4]对相关圆柱齿轮(如直齿轮、斜齿轮)、螺旋锥齿轮的精度测量方法及其特点进行了综述,通过对比分析各测量方法,认为三坐标测量方法具有较大优势,并指出了该测量方法的优越性。
T. Pfeifer等人[5]利用三坐标测量机测量了螺旋锥齿轮的齿面三维坐标数据,并据此开发了算法程序以补偿测头导致的误差,且在此基础上分析了含齿形修形、鼓形修形及制造误差的 0 阶、1 阶、2 阶偏差。
2)国内已有研究
国内对于面齿轮的研究相对较晚,尚处于起步阶段,因而对于面齿轮齿面偏差方面的研究相对较少,但是也取得了一定的成果。
王延忠等人[6]的研究中,提出了在齿轮测量仪KLINGE-INBERGP100上对齿轮齿形进行偏差测量,为面齿轮精度的评定提供了依据。
王小椿等人[7]提出了三坐标测量方法。其研究中不仅给出了Gleason制螺旋锥齿轮的理论齿面模型,且用差曲面描述了三坐标测量机测量得到的实际齿面到理论齿面的偏差,提出了一种利用差曲面特征参数修正机床调整参数的新方法,以有效提高齿面几何精度。
王军[8]对双曲面齿轮齿面加工精度控制方法进行了深入研究,其应用差曲面的空间参数对螺旋锥齿轮齿面误差进行了修正。
王志等人[9]研究了采用坐标测量机测量面齿轮齿面误差时由于测量坐标系和面齿轮设计坐标系不重合造成的误差,分析了坐标测量机测头直径对测量误差的影响。
相对于其他的齿轮测量仪器,三坐标测量仪既可以通过测量软件对齿面误差进行测量,还可以通过误差分析得到各种误差信息。因此,本文拟通过三坐标测量仪得到面齿轮齿面的测量实际数据和齿面偏差,并对建立的齿面误差识别方程求解,以达到减小面齿轮齿面误差的目的。
2 面齿轮齿面数学模型和齿面网格节点计算
本研究在六轴五联动的数控磨齿机QMK50A上,采用蝶形砂轮磨削正交面齿轮,面齿轮的材料选用18Cr2Ni4WA,其基本参数如表1所示。
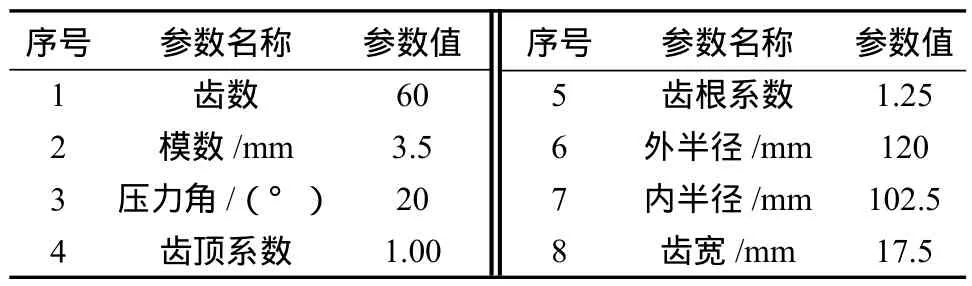
表1 正交面齿轮基本参数Table 1 Basic parameters of orthogonal face gears
2.1 齿面数学模型的建立
根据碟形砂轮的磨削面齿轮原理,其虚拟插齿刀是替代小圆柱齿轮与面齿轮啮合展成加工出面齿轮齿面的,因而其渐开线圆柱齿轮的齿面方程可以用于表示刀具的齿面方程[9]。渐开线刀具的齿廓截面参数如图1所示。

图1 渐开线刀具齿廓截面参数Fig. 1 Tooth pro fi le section parameters of the involute cutter
如图1所示的渐开线刀具齿廓截面参数设置中,设渐开线上任意一点的法矢为ns,插齿刀具的基圆半径为rbs,任意一点的法矢与基圆切点到渐开线起始点之间的圆心角为θs,刀具在齿槽上的对称线和渐开线起始点之间的夹角为θs0,ab和cd是分别对应于刀具两侧齿槽的渐开线,us为沿刀具轴线Zs的齿宽参数。
根据以上的参数设置,可以得出渐开线刀具的齿面方程rs为

式中:“±”分别对应于渐开线ab和渐开线cd;
渐开线刀具齿面上任意一点的单位法矢ns可以表示如下:
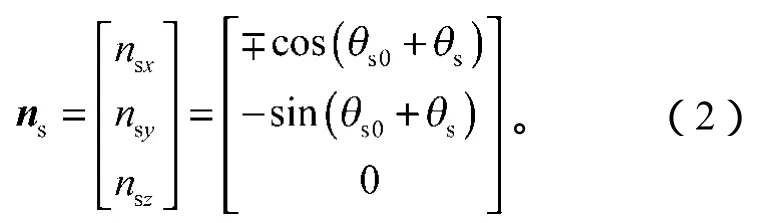
面齿轮的展成坐标系如图2所示。在图2所示面齿轮展成坐标系中,对面齿轮和插齿刀具的运动坐标系做了重合处理。其中:Sm—Omxmymzm和Sp—Opxpypzp均为固定坐标系,也是辅助坐标系;S2—O2x2y2z2和Ss—Osxsyszs分别是面齿轮和插齿刀具固联的坐标系;γm为面齿轮和插齿刀具轴线间的夹角;φ2和φs分别表示加工时面齿轮和插齿刀具各自的转角。
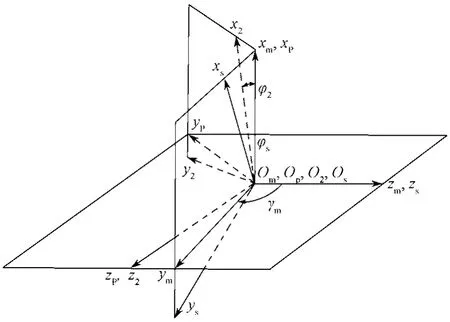
图2 面齿轮的展成坐标系Fig. 2 Generating coordinate system of face gears
插齿刀具坐标系Ss到面齿轮坐标系S2间的变换矩阵如下:
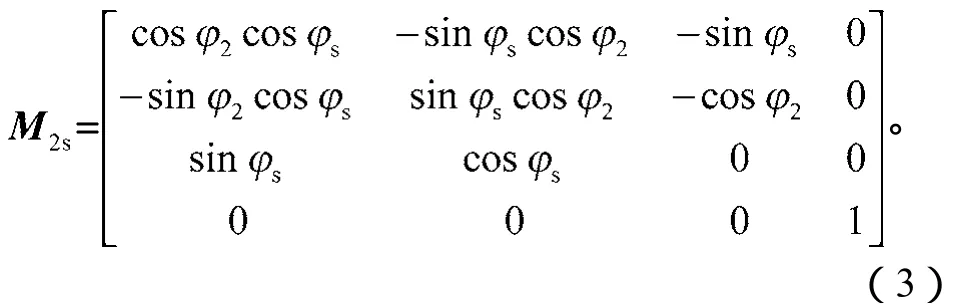
根据齿轮啮合原理和坐标系转换方法,将插齿刀具齿面方程进行转换,得到面齿轮的齿面方程,为
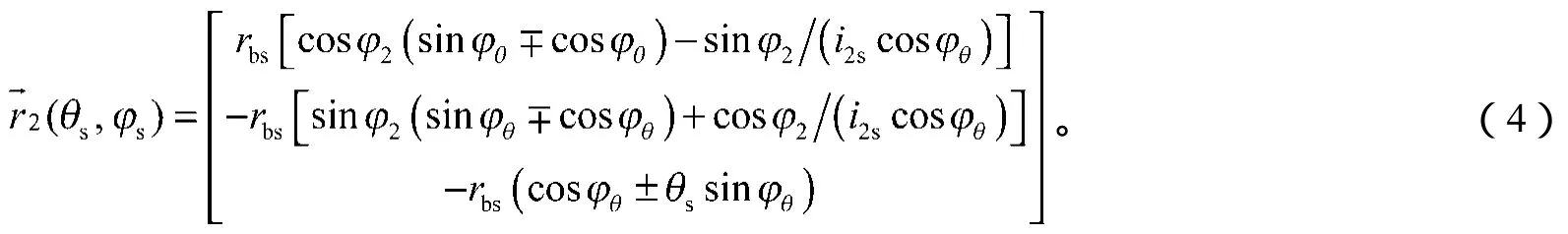
式(3)~(4)中:

2.2 面齿轮齿面的网格划分与节点计算
面齿轮是复杂的齿面,为能准确计算出齿面坐标的理论值,并且对其进行准确地测量,需要先对其齿面进行网格划分。本研究中,面齿轮齿面上的网格划分如图3所示。

图3 面齿轮齿面上的网格划分Fig. 3 Grid division on tooth surface
在对面齿轮进行齿面网格划分时,应将网格的边界在齿廓和齿长方向适当向内收缩,以规避测量探针的球头在非工作面上的干涉而产生的误差。为了使测量齿面为工作齿面,规定在轴截面的齿高方向向内收缩5% ,在齿长方向的大端和小端分别向内收缩10%[6],如图4所示,其中P11、P19、P51、P59分别为网格的边界点。
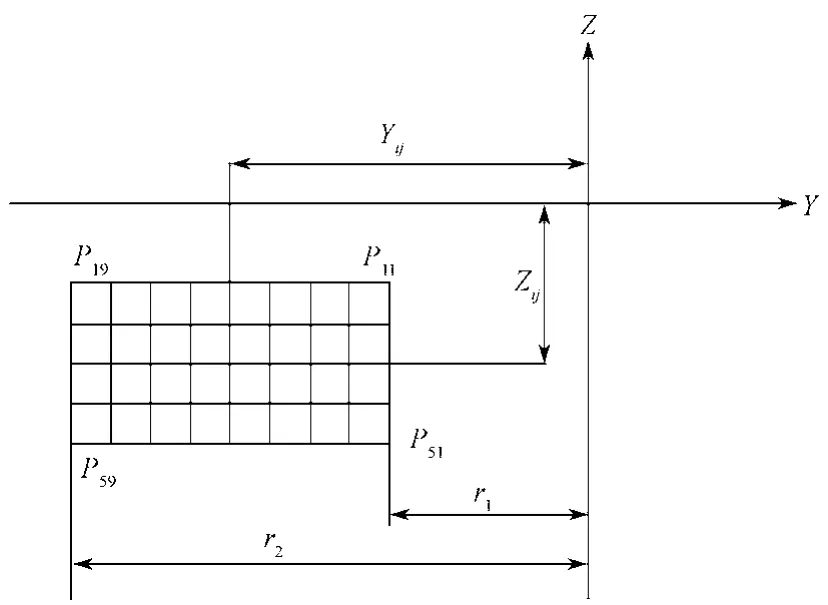
图4 面齿轮齿面轴截面的网格划分Fig. 4 Grid division in axial section
面齿轮齿面网格中任意一点的表达式可以式(5)表示,其中i=1~5,j=1~9。

其中,R1为最小内半径,R2为最大外半径,u为齿宽,且u=R2-R1;
h=0.08H,其中H为面齿轮齿高,且H=3.5 m。
从刀具坐标系Ss—Osxsyszs转换到面齿轮坐标系S2—O2x2y2z2中,便可以得到轴截面网格投影在齿面上的网格节点的45个理论坐标值(x2,y2,z2),如表2所示。节点坐标值在两个坐标系转换时的关系可以表示如下:
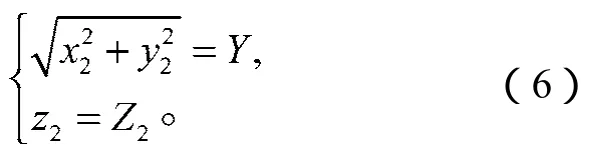
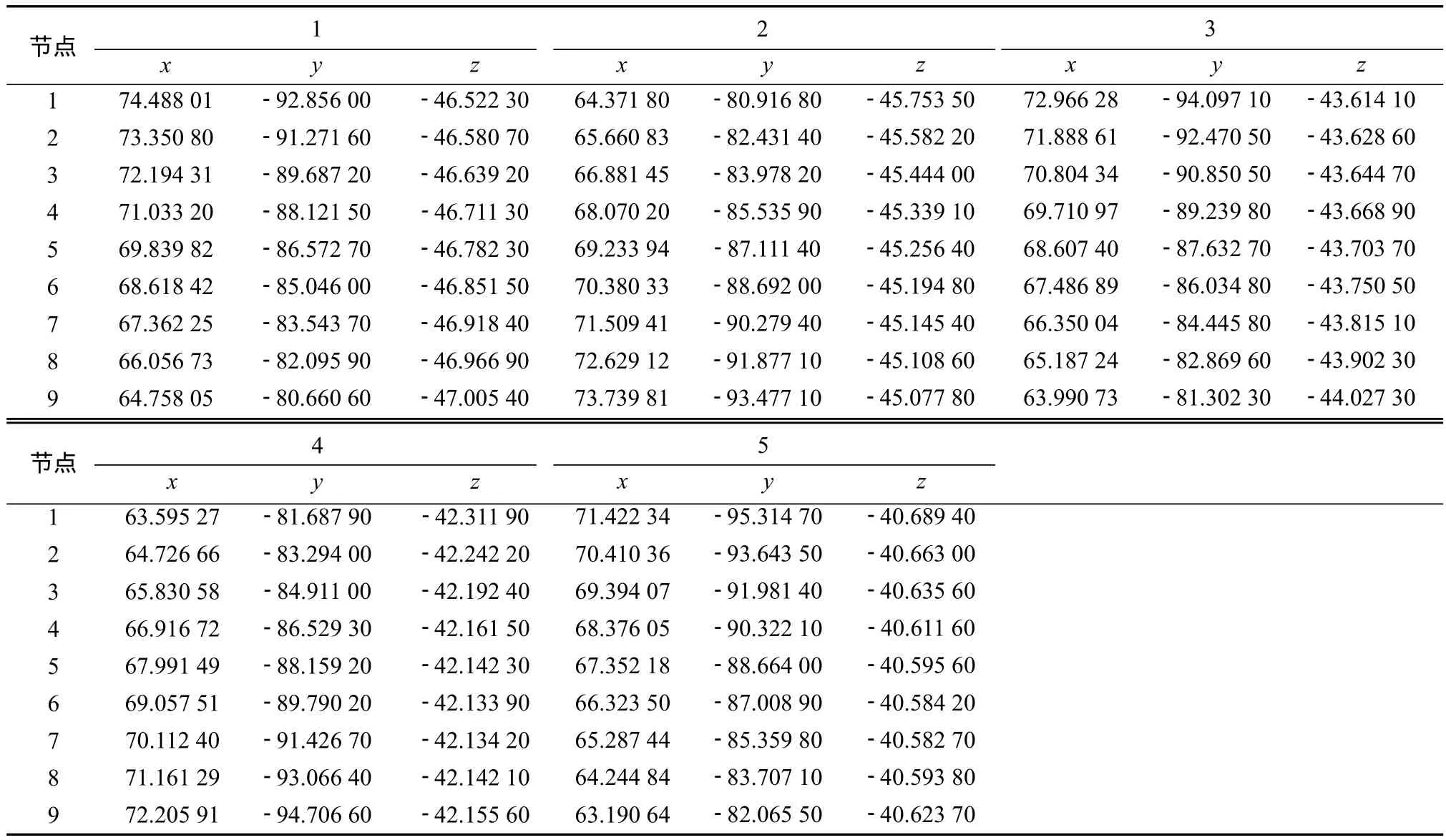
表2 齿面网格节点坐标理论值Table 2 Theoretical coordinate values of grid nodes of the tooth surfacemm
3 面齿轮齿面的三坐标测量
为对齿面网格节点坐标实际值进行测量,采用三坐标测量仪Xorbit plus 77,其测头直径为0.5 mm。三坐标测量的坐标系如图5所示,选择内孔的圆柱面轴向为z向。
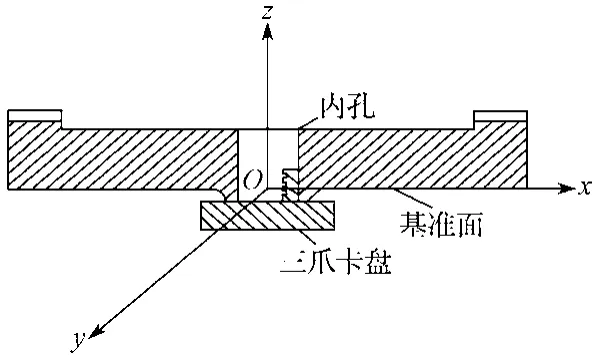
图5 三坐标测量的坐标系Fig. 5 Coordinate system in CMM
在三坐标测量仪上测量齿面真实坐标值的时候,其基准面为z向,齿坯底面为x、y向,其测量示意如图6所示。

图6 三坐标测量示意图Fig. 6 Schematic diagram of coordinate measuring
经测量,面齿轮一个齿面的45个节点坐标测量值如表3所示。
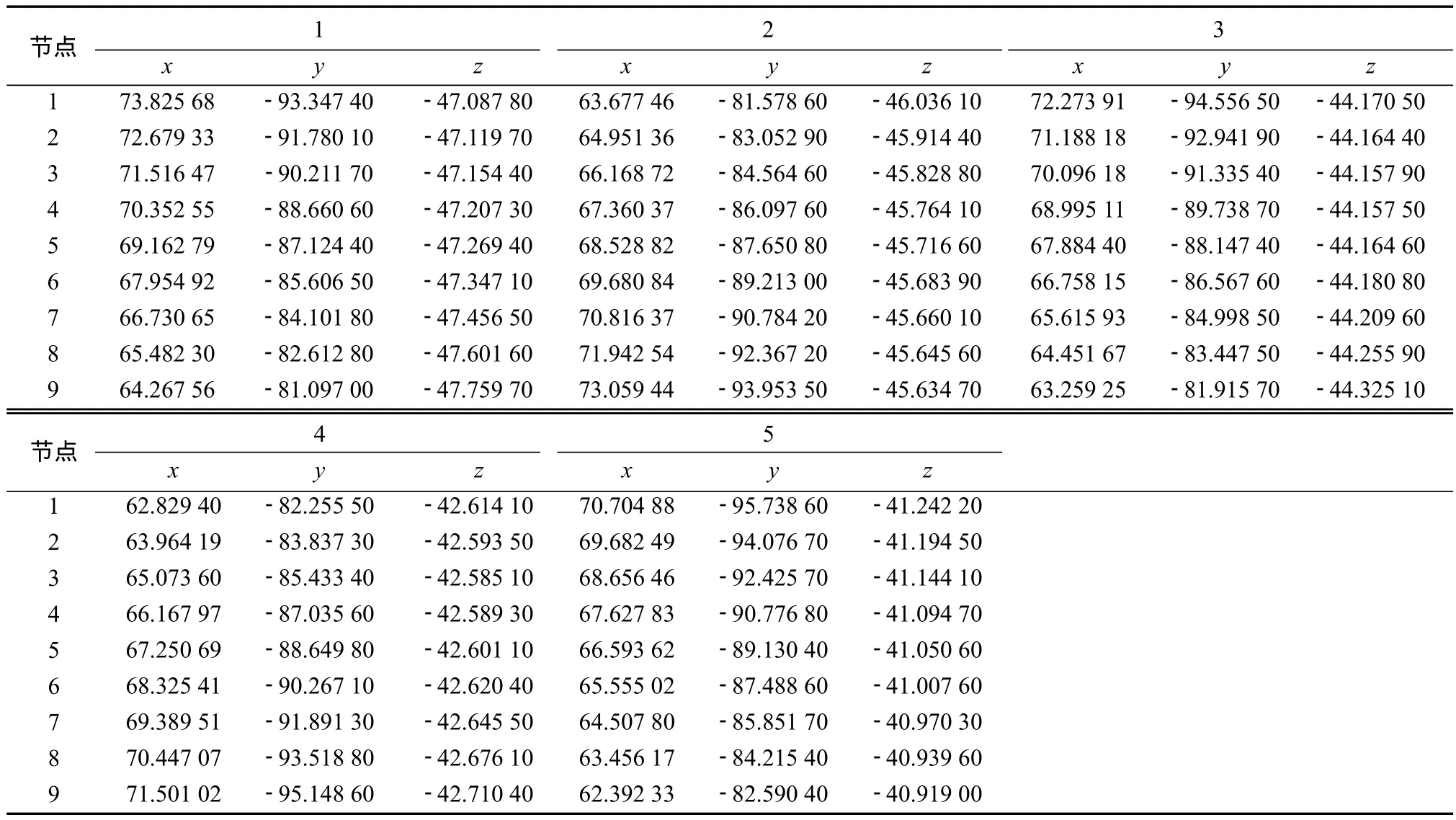
表3 齿面网格节点坐标测量值Table 3 Measuring coordinate values of grid nodes of the tooth surfacemm
4 齿面误差的SQP法修正与实验
4.1 齿面误差的处理
如图7所示,齿面误差是齿面上网格节点处的理论齿面和实际齿面的法向误差,是一个几何量。即理论齿面上点A与其法向n和实际齿面的交点C的距离,而实际所测得的齿面误差是点A与实际齿面的点B之间的距离,但由于点B与点C之间的距离很近,所以可以认为[10]。
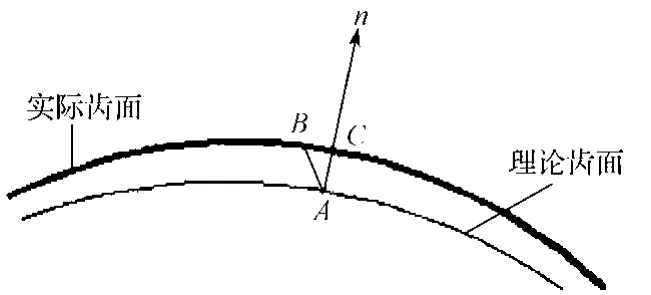
图7 齿面法向误差Fig. 7 Normal errors of the tooth surface
为了建立机床加工参数和齿面法向误差之间的关系,需将测得的几何量转化为能表示齿面误差的代数量。一般情况下,齿面误差分为齿距误差和齿形误差。齿距误差一般由以下两种原因产生:一是加工及热处理时产生的形变,其可通过磨削前工序进行修正;另一主要原因是由机床的分度误差引起的。由于分度误差是机床的固有误差,连续分度后齿轮同一侧的齿距误差是相同的,因而分度误差引起的齿距误差相对平稳,所以可以通过提高机床分度精度的方式来减小齿距误差对测量结果的影响。可见,齿形误差是影响齿面误差测量结果的主要因素。
齿面误差分解如图8所示。其中,F3表示理论齿面,F1表示磨削后含有齿面误差的实际齿面,F2表示将实际齿面F1绕轴线旋转一定角度后,与理论齿面F3在齿面45个节点的中间点(即第3行第5列点)重合时的齿面。通过三坐标测量仪测得齿面网格各节点处的法向偏差见表4。
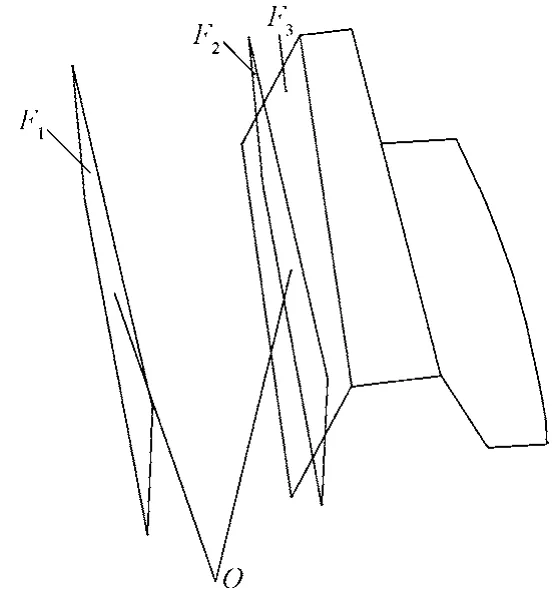
图8 齿面误差分解Fig. 8 Error analysis of the tooth surface
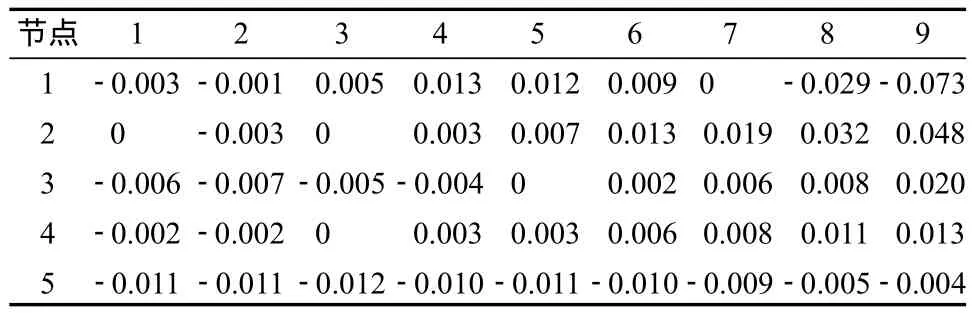
表4 齿面网格节点处的法向偏差Table 4 Normal deviation of grid nodes of the tooth surface mm
4.2 面齿轮磨削坐标系的建立
建立如图9所示的坐标系,以确定面齿轮磨削时刀具和零件的位置关系[11]。
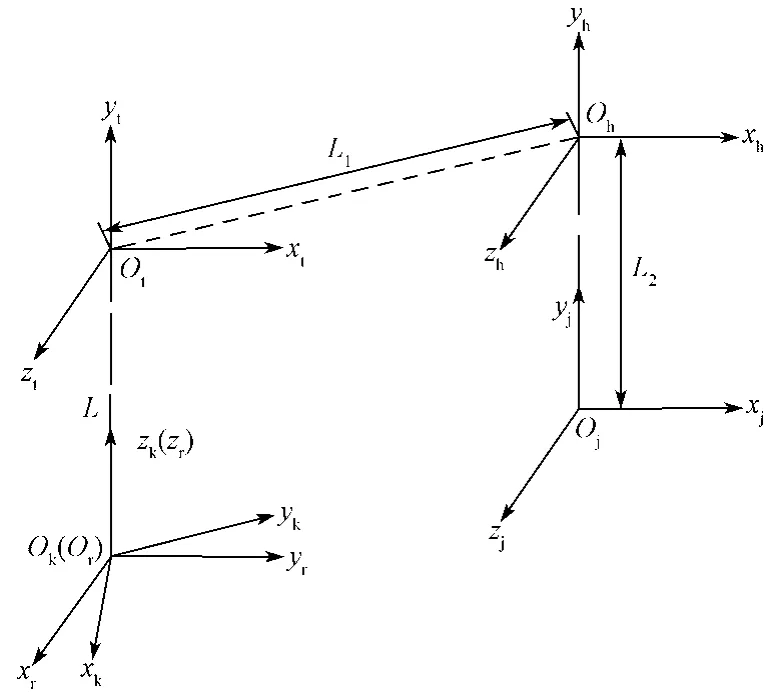
图9 面齿轮与砂轮的位置关系Fig. 9 Positional relationship between face gears and grinding wheels
图9中,Sk—Okxkykzk为面齿轮的初始位置,Sr—Orxryrzr为面齿轮的动坐标系;St—Otxtytzt为蝶形砂轮的初始位置;Sh—Ohxhyhzh为砂轮沿面齿轮齿高方向进给形成的动坐标系,Sj—Ojxjyjzj为砂轮沿面齿轮齿长方向进给形成的动坐标系。L1为蝶形砂轮固定坐标系St—Otxtytzt和齿高方向动坐标系Sh—Ohxhyhzh原点间的距离,L2为齿高方向动坐标系Sh—Ohxhyhzh和齿长方向动坐标系Sj—Ojxjyjzj原点间的距离,L为蝶形砂轮的初始位置St—Otxtytzt和面齿轮的初始位置Sr—Orxryrzr原点间的距离。
4.3 齿面误差识别方程的建立
由面齿轮和砂轮的位置关系可以得知,动坐标系Sj—Ojxjyjzj到面齿轮的转动坐标系Sr—Orxryrzr的变换矩阵Mjr可表示为
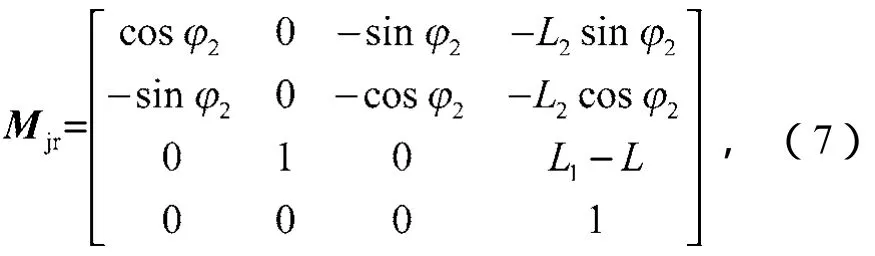
则包含磨床误差的面齿轮齿面方程可以表示为
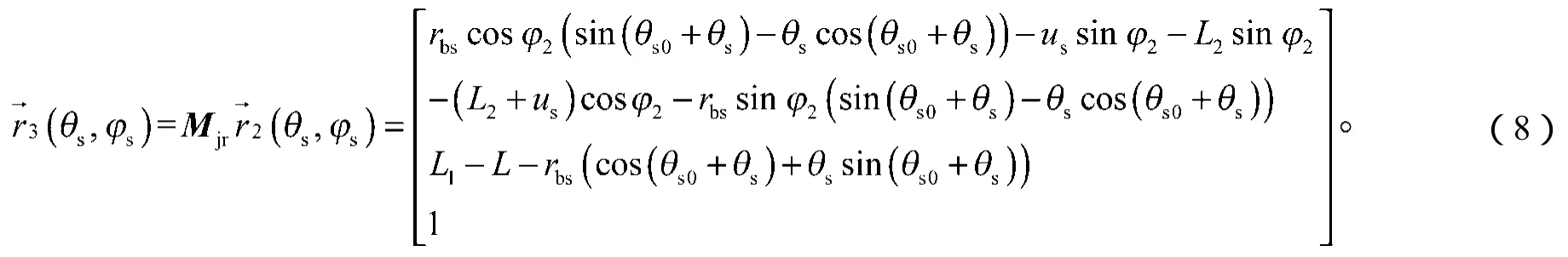
面齿轮齿面的法向矢量方程为

面齿轮齿面误差的产生主要是由机床的误差引起的,对面齿轮的齿面偏差进行修正就需要对机床的调整误差进行修正。根据式(8)可得
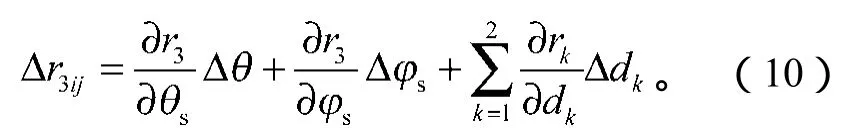
式中:i为齿面网格点的行数;
j为齿面网格点的列数;
dk(k=1, 2)为引起齿面偏差的机床加工参数,且d1=L1,d2=L2。
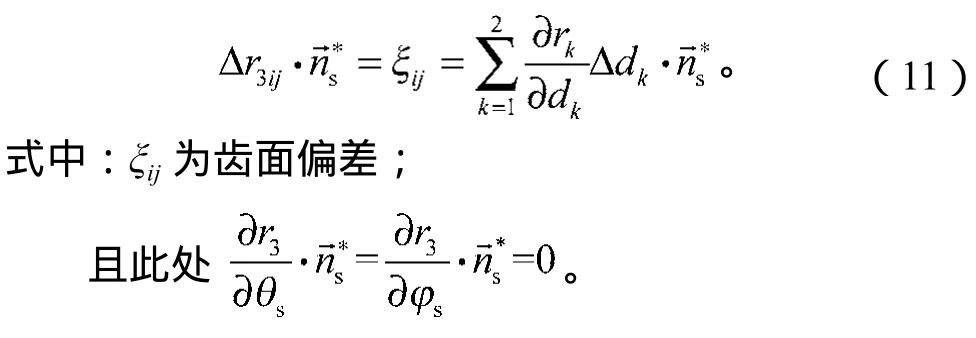
将测量所得的45个齿面偏差值代入式(11),可得到一个方程组,通过对该方程组的求解,就可对机床加工参数进行相应调整,从而达到对齿轮齿面进行修正的目的。
4.4 对超定方程的求解方法
由于所测量的齿面偏差值有45组,而所求的未知数为机床加工参数,齿面偏差值的数量大于机床加工参数的数量,则该方程组为一个超定方程组,采用一般的解法无法求解得到精确的机床加工参数[7]。对于该超定方程,本研究采用序列二次规划(sequence quadratic program,SQP)方法进行最优求解,即将齿面偏差值代入方程(11),得到机床加工参数的最优解,使得面齿轮的齿面误差最小。
由公式(11)可以确定目标函数,为
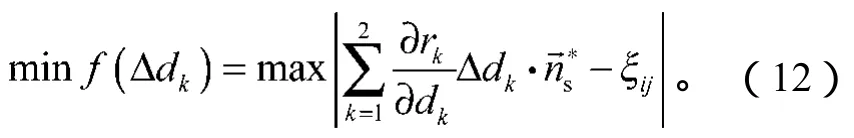
经SQP方法求解,可以得出L1=7.875 mm,L2=12.740 mm。
通过对L1和L2值进行修正后,齿面误差明显改善,如图10所示。由图10 可看出,齿面工作区域部分的齿面误差总体趋于平稳,但靠近齿面过渡区域还需进一步改善。

图10 修正后的齿面误差Fig. 10 Corrected tooth surface errors
5 结论
1)根据齿面啮合原理及面齿轮展成坐标系的关系,得到了面齿轮齿面方程,并通过对齿面进行网格划分和节点计算,得到齿面网格节点坐标理论值。
2)在三坐标测量机上测出了齿面节点的坐标测量值,经齿面误差的分析和分解,得到了齿面网格节点处的齿面偏差。
3)根据面齿轮磨削坐标系之间的关系,建立了面齿轮含齿面误差的识别方程,采用SQP方法对识别方程进行求解,得出了机床磨削参数L1和L2的优化值,减少了正交面齿轮的磨削齿面误差,达到了齿面修正的目的。
[1]LITVIN F L,FUENTES A,HOWKINS M. Design,Generation and TCA of New Type of Asymmetric Face-Gear Drive with Modified Geometry[J]. Computer Methods in Applied Mechanics and Engineering,2001,190(43/44):5837-5865.
[2]MING Xingzu,GAO Qin,YAN Hongzhi,et al.Mathematical Modeling and Machining Parameter Optimization for the Surface Roughness of Face Gear Grinding[J]. The International Journal of Advanced Manufacturing Technology,2017,90(9/10/11/12):2453-2460.
[3]LITVIN F L, CHEN Y J,HEATH G F,et al.Apparatus and Method for Precision Grinding Face Gear:US 6.146.235[P]. 2000-11-14.
[4]GOCH G. Gear Metrology[J]. CIRP Annals:Manufacturing Technology,2003,52(2):659-695.
[5]PFEIFER T,KUROKAWA S,MEYER S. Derivation of Parameters of Global Form Deviations for 3-Dimensional Surfaces in Actual Manufacturing Processes[J]. Measurement,2001,29(3):179-200.
[6]王延忠,王庆颖,吴灿辉,等. 正交面齿轮齿面偏差的坐标测量[J]. 机械传动,2010,34(7):1-4.WANG Yanzhong,WANG Qingying,WU Canhui,et al. Deviation of Face Gear Real Tooth Surface Determined by Coordinate Measurements[J]. Journal of Mechanical Transmission,2010,34(7):1-4.
[7]王小椿,王 军,姜 虹,等. 螺旋锥齿轮的齿面测量及机床加工参数修正[J]. 机械工程学报,2003,39(8):125-128.WANG Xiaochun,WANG Jun,JIANG Hong,et al.Tooth Surface Measurement and Machine-Settings Correction of Spiral Bevel Gear[J]. Chinese Journal of Mechanical Engineering, 2003,39(8):125-128.
[8]王 军. 基于三坐标测量的弧齿锥齿轮及准双曲面齿轮齿面加工精度控制方法研究[D]. 西安:西安交通大学,2003.WANG Jun. A Study on the Tooth Surface Geometrical Precision Control of Spiral Bevel and Hypoid Gears Based on 3D Coordinate Measuring[D]. Xi’an:Xi’an Jiaotong University,2003.
[9]王 志,石照耀. CMM 测量正交面齿轮的误差理论分析[J]. 北京工业大学学报,2012,38 (5):663-667.WANG Zhi,SHI Zhaoyao. Theory Analysis of Error in Orthogonal Face Gear Measurement by CMM[J]. Journal of Beijing University of Technology,2012,38(5):663-667.
[10]陈书涵,严宏志,贺尚红. 螺旋锥齿轮真实齿面偏差修正研究[J]. 制造技术与机床,2011 (3):87-90.CHEN Shuhan,YAN Hongzhi,HE Shanghong.Research on Real Tooth Surface Deviation Correction of Spiral Bevel Gear[J]. Manufacturing Technology &Machine Tool,2011(3):87-90.
[11]王延忠,侯良威,兰 州,等. 渐开线碟形砂轮磨削面齿轮数控加工研究[J]. 航空动力学报,2015,30(8):2033-2040.WANG Yanzhong,HOU Liangwei,LAN Zhou,et al. Research on Processing Method of Grinding Face Gear with Involute Disc Wheel[J]. Journal of Aerospace Powe,2015,30(8):2033-2040.
(责任编辑:廖友媛)
Study on Tooth Surface Error Correction of NC Grinding of Orthogonal Face Gears
FANG Shuguang,MING Xingzu,WANG Hongyang,LUO Dan
(School of Mechanical Engineering,Hunan University of Technology,Zhuzhou Hunan 412007,China)
Firstly, based on the meshing principle and the transformation relationship between generating coordinate system of NC grinding, the mathematical model of tooth surface of face gears can be derived, followed by a division of the tooth surface grids of face gear in 5×9, and a calculation of the theoretical coordinate values of nodes. Then three coordinate measuring machines (CMM) are used to measure the coordinate values of the grinding tooth surface joints, and tooth surface deviations of grid nodes can be obtained by analyzing and decomposing the tooth surface error. With the identi fi cation equation of the tooth surface error having been established, the sequential quadratic programming (SQP) method has been proposed to optimize the machining parameters of the machine tool, thus completing the correction of the tooth surface error of the opposite gears. The result of tooth surface error correction shows that the error of tooth surface in the working area tends to be stable, and the corrected tooth surface error is obviously improved, but the transition area near the tooth surface needs further improvement.
face gear;tooth surface deviation;coordinate measuring machine(CMM);grinding parameter;sequential quadratic programming(SQP)
TP215
A
1673-9833(2017)04-0001-07
10.3969/j.issn.1673-9833.2017.04.001
2017-05-26
国家自然科学基金资助项目(51375161),湖南省自然科学基金资助项目(2017JJ4023)
方曙光(1991-),男,湖北黄冈人,湖南工业大学硕士生,主要研究方向为数字化制造技术,E-mail:858211527@qq.com
明兴祖(1964-),男,湖南临澧人,湖南工业大学教授,博士,硕士生导师,主要从事数字化制造与装备技术方面的教学与研究,E-mail:mxz9036@126.com
