环境污染与自然资源耦合系统的动力学模型分析
2017-10-18顾恩国鲁嘉珺
顾恩国,鲁嘉珺
(中南民族大学 数学与统计学学院,武汉 430074)
环境污染与自然资源耦合系统的动力学模型分析
顾恩国,鲁嘉珺
(中南民族大学 数学与统计学学院,武汉 430074)
为研究环境自净率和污染物排放速度对自然资源存量的影响,建立了自然资源与环境污染耦合系统的离散动力学模型,讨论了正平衡点的存在性、稳定性及局部分叉,应用中心流形理论探讨了不动点在发生flip分叉时的临界稳定性,并用数值模拟的方法验证了正平衡点的局部分叉.最后,用全局分析方法描述了环境自净率对自然资源可持续利用的影响.
自然资源;污染物;正平衡点的稳定性;flip 分叉;中心流形;可行吸引域
AbstractA discrete dynamic model of the coupled system of natural resources and environmental pollution was established, and the influence of environmental self-purification rate and pollutant emission rate on the stock of natural resources was analyzed. The existence, stability and local bifurcations of positive fixed points were investigated, the critical stability of fixed point in flip bifurcation was analyzed by using the center manifold theory, and numerical simulation was used to verify the local bifurcations of fixed point. At last, the global method was used to analyze the influence of environmental self-purification rate on the sustainable utilization of the natural resources.
Keywordsnatural resources; pollutants; stability of the positive equilibrium point; flip bifurcation; center manifold; feasible domain
随着人口的增长和社会经济的发展,对生态系统造成的冲击越来越强.自然资源和服务的可持续性问题, 其重要性和紧迫性已经引起了生态学家和经济学家的广泛关注[1,2],自然资源的可持续利用已经成为非常重要的研究课题.在国内外,关于自然资源可持续发展的研究很多,学者们建立了大量数学模型[3-6],将自然资源与环境污染耦合起来建立动力学模型并且用离散动力学方法进行研究的成果却很少,对其演化进行全局分析的更微乎其微.陈六君在文献[7]中建立了自然资源环境系统的连续动力学模型,并对模型所反映的突变性质及其经济意义进行了分析.本文在假设人类提取自然资源是自然资源储量的线性函数的情况下,建立了自然资源储量与污染物浓度相互作用的二维离散动力学模型,用来研究环境自净率和污染物排放速度对自然资源储量的影响,进而讨论对自然资源可持续利用的影响.
1 模型的建立
本文假设自然资源增量在不考虑生物死亡和人类索取情况下满足Logistic律:
N(t+1)-N(t)=rN(t)[1-N(t)/K],
其中N(t)为在时刻t自然资源存量,r为自然资源再生率;K为最大自然资源存量.假设污染物浓度增量与人类向环境系统输入污染物的速度和环境自净率有关:D(t+1)-D(t)=p-cD(t)N(t),D(t)为在时刻t污染物浓度;p为人类向环境系统输入污染物的速度;c为单位自然资源存量的自净率.假设人类对自然资源的提取速度H(t)与自然资源存量呈线性关系,令H(t)=αN(t),其中α为资源提取的速度.同时污染浓度会影响自然资源的再生能力,利用文[7]中的Hill函数,假设生物死亡函数:F(t)=fN(t)D(t)/(D(t)+D0),f为致死率.根据上述假设和说明,建立系统模型如下:

(1)
2 正平衡点的存在性和稳定性
二维动力系统(1)可以写成一个映射动力系统:
(2)
根据平衡点的定义,系统(2)的平衡点就是下面非线性方程组的解:
(3)
由方程组(3)得:

(4)


(5)
联立(4)和(5)式得到方程cK(r-μ-f)D2+[cK(r-μ)D0-μf]D-rpD0=0.
记a=cK(r-μ-f)≥0,b=cK(r-μ)D0-μf,Δ=b2+4arpD0>0.
关于正平衡点的存在性,可有下面的命题1.
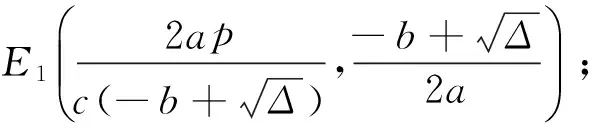

由命题1知道系统(2)存在一个唯一的正不动点,但这不足以得出自然资源可持续利用.为了得到自然资源可持续利用的条件,讨论系统(2)的唯一平衡点的稳定性.
系统(2)的Jacobian 矩阵是:
注意(4)和(5)式,Jacobian矩阵化简为:

如果所有特征值在复平面上位于单位圆内,则不动点渐近稳定,由Jury条件,若不动点满足条件:
则系统(2)正平衡点是渐近稳定的.这3个条件对应着特征值在复平面上以3种方式越过单位圆:若p1<0,至少有一个特征值大于1;若p2<0至少有一个特征值小于-1;若p3<0,有一对共轭复特征值位于单位圆外.它们等于0分别对应着fold、flip、Neimark分叉.
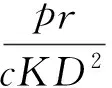
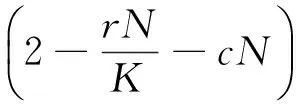


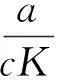

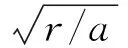
综上所述,可得到关于正不动点稳定的命题2.


取参数K=4,r=2,f=0.2,D0=0.5,μ=0.3,p=0.2,c=0.4,显然r=2>0.5=f+μ, 正不动点E1(3.3071,0.1512)渐近稳定.图1给出了参数为K=4,r=2,f=0.2,D0=0.5,μ=0.3,p=0.2时p1(c),p2(c),p3(c),0 图1 p1(c),p2(c),p3(c),0 图2 关于c的一维分叉图Fig.2 One dimensional bifurcation diagram with c 图3 一维或二维分叉图 Fig.3 One or two dimensional bifurcation diagram 当参数集满足p2=0时,在正不动点E1处出现flip分叉.接下来通过中心流形理论确定正不动点的稳定性.取K=4,r=2,f=0.2,D0=0.5,μ=0.3,p=0.2,c=0.5525,此时参数集满足p2=0, 正不动点为E1(3.3285,0.1087). 首先,将系统(2)的正不动点E1通过平移换转换到原点O(0,0),则原系统(2)化为: 所以系统(6)在E1(3.3285,0.1087)处的Taylor展式(忽略高阶余项)为: (7) 将上述方程组写成矩阵形式为: (8) 其中系数矩阵为: (9) 其中: 根据中心流形的定义,令: v=h(u)=αu2+βu3+O(u4), (10) 则h(Mu+f1(u,h(u)))-Nh(u)-g1(u,h(u))=0. (11) 其中,M=-1,N=0.2238,f1(u,h(u))=0.4989u2+0.1408αu3+O(u4),h(Mu+f1(u,h(u)))=h(-u+f1(u,h(u)))=αu2+(0.9978-β)u3+O(u4), Nh(u)=0.2238(αu2+βu3+O(u4)),g1(u,h(u))=0.0338u2-0.4152αu3+O(u4), 将上式代入方程(11)得: 求得中心流形为: h(u)=0.4355u2+0.5952u3+O(u4). (12) 系统(9)在中心流形Mc的限制为: f:u|→-u+f(u,h(u))=-u+0.4989u2- 0.0641u3+O(u4). (13) 映射f在原点处的Schwarzian导数为: (14) 因此h(u)为稳定流形,从而正不动点E1稳定. 通过对正平衡态可行吸引域的性质的分析,可以得出自然资源的自净率在怎样的条件下是维持资源可再生能力还是最终导致资源枯竭.本文我们主要采用数值模拟的方法来分析系统(2)的可行吸引域结构, 根据系统(2)所代表的实际意义, 我们仅研究轨线完全在Ω={(N,D)|N>0,D∈R}中的N和D满足的初始条件.若资源的存量是非正值,对自然环境资源的可持续利用将无法实现,通过数值试验,可以研究随着自然资源自净率变化的可行吸引域的变化情况. 图4给出了自然资源可行吸引域的吸引子,选取的参数除p,c外与局部分析的值一样,即K=4,r=2,f=0.2,D0=0.5,μ=0.3. 在图4(a)-(c)中,黑色表示有界吸引子,白色区域表示有界吸引子的吸引域,深灰区域表示无穷吸引子的吸引域. 图4(d)表明p=0.69,c=0.55时,不动点与周期2轨道两个有界吸引子共存,白色区域表示不动点(空心点)的吸引域,浅灰区域表示周期2轨道(实心点)的吸引域. 图4 可行吸引域和吸引子Fig.4 Feasible domains of attraction and attractors 本文建立了自然资源与环境污染耦合的离散动力学模型,对模型进行了非线性动力学分析,讨论了正平衡点的存在性、稳定性及局部分叉,并对正平衡态进行了全局分析.研究发现:系统(2)具有混沌和共存吸引子复杂的动力学行为,并且自然资源自净率和人类向环境系统输入污染物的速度对可再生资源的可持续利用具有显著影响,当它们都不太大时,系统(2)始终稳定在正平衡点(见图3(a)),并具有较大的可行吸引域的面积(见图4(a)),因此针对不同的自然环境因素,要保证自然资源的可持续利用,需要结合自然资源的自净率,控制人类向环境系统输入污染物的速度,这对于自然资源管理决策者制定资源利用、保护政策具有重要的参考意义. [1] Food and Agriculture Organization. The state of world fisheries and aquaculture[R]. Sofia: FAO, 2004. [2] Garcia,Grainger J R.Gloom and doom? The future of marine capture fisheries[J].Philosophical Transactions of the Royal Society,2005, B360:21-24. [3] Clark C W. Mathematical bioeconomics: the optimal management of renewable resources[M].New York:Wilery,1976. [4] Bischi G I,Kopel M,Szidarovszky F. Expectation-stock dynamics in multi-agent fisheries[J].Annals of Operations Research,2005,137:299-300. [5] Kar T K,Matsuda H. A bioeconomic model of a single-species fishery with a marine reserve[J].Journal of Environmental Management,2008,86:171-180. [6] Bischi G I, Szidarovszky F. Harvesting dynamics in protected and unprotected areas[J].Journal of Economic and Organization,2007,62:370-384. [7] 陈六君,方福康. 自然资源环境系统的突变机制[J].复杂系统与复杂性科学,2004,1(2):1-8. DynamicModelAnalysisofCoupledSystemofEnvironmentalPollutionandNaturalResources GuEnguo,LuJiajun (College of Mathematics and Statistics, South-Central University for Nationalities, Wuhan 430074, China) O192;F062.1 A 1672-4321(2017)03-0142-05 2017-06-20 顾恩国(1964-),男,教授,研究方向:非线性动力系统应用,E-mail: guenguo@163.com 国家自然科学基金资助项目(61374085);中央高校基本科研业务费专项基金资助项目(CZP17016)


3 产生flip分叉时正不动点的稳定性分析

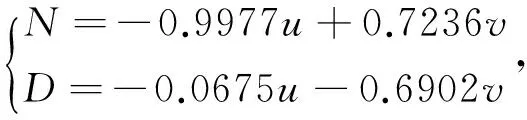

4 系统的全局分析

5 结语
