接入实时降雨数据的暴雨型洪涝灾害临灾预警方法

杜志强，王 叁，张叶廷

(1.武汉大学 测绘遥感信息工程国家重点实验室，湖北 武汉 430079；2.地球空间信息技术协同创新中心，湖北 武汉 430079)

0 引 言

洪涝灾害在我国是第二重要的气候灾害，它严重威胁了人民的生命财产安全并为经济发展带来极大的影响[1]。暴雨降水是我国洪涝灾害发生的直接原因。洪涝灾害总是在几场大降水之后迅速发生，并且灾害前期降水的致灾性较大[2]。临灾预警，即在临近灾害发生的时期进行短时预警，一方面有效提升了洪涝灾害预警的时效性，另一方面为居民转移安置提供足够及合理的时间。在暴雨型洪涝灾害发生的前期进行临灾预警，对于控制灾情以及减少灾害造成的危害和损失等方面都具有重要的意义。

现有暴雨型洪涝预警研究大致可分为三类。第一类是聚焦暴雨降水，利用遥感手段预警强降雨[3-5]，但这种方法仅仅通过预警暴雨降水量和范围来预警洪涝，未能有机结合暴雨和洪涝灾害之间的机理关系；第二类是结合水文模型进行数值模拟[6-10]，这种方法对河网流域的洪涝预警效果好，但是对数据和模型参数的要求较高，某些参数获取难度较大，且不适用于城市内涝的预警；还有一类是运用GIS的空间分析能力，从致灾因子、孕灾环境、承灾体以及防灾减灾能力等方面进行分析，构建区域风险评价模型[11-14]，但是目前这种方法对影响因子的选取理论还不够成熟，存在致灾因子致灾性不明确问题，如通常将暴雨作为致灾因子，但是暴雨与洪涝灾害之间并不完全是因果关系。此外，当前的暴雨型洪涝风险分析方法大多是省级的年度洪涝风险分析，时间尺度和空间尺度都比较大，时效性和针对性较差，难以满足局部强降雨导致的洪涝灾害预警需求[15-18]，对当前或即将发生的灾害指导意义有限。

本文针对现有暴雨型洪涝灾害预警方法时效性差，空间尺度大以及致灾因子的致灾性不明确的问题，通过接入实时降雨量数据，以“日”为时间尺度，将异常降雨作为致灾因子进行暴雨型洪涝临灾风险分析。借助时序分析模型分析局部地区的正常降雨规律进而识别异常降雨，并与地形起伏、高程和河网因素结合，构建暴雨型洪涝灾害风险指数。根据暴雨型洪涝灾害风险数值大小将灾害风险等级划分为无风险、低风险、中风险、中高风险和高风险5个等级，得到逐日风险区划图，实现在灾害发生前期进行临灾预警，为防灾减灾提供科学的参考信息。

1 实验区域与数据

1.1 实验区域概况

清远市位于广东省中部，一半以上地域是山区，地势自西北向东南倾斜，以山地、丘陵为主，平原分布于北江两岸的南部地区。该地区处于北回归线北侧附近，属东亚亚热带季风气候区，年平均降雨量1900 mm。清远市行政区划如图1所示，现辖清远市区（清城区、清新区）、佛冈县、阳山县、连南瑶族自治县、连山壮族瑶族自治县，并代管英德市、连州市两个县级市。

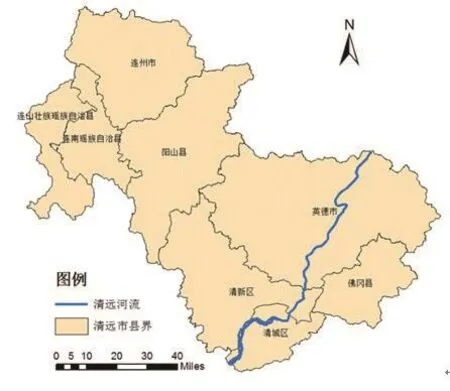
图1 广东省清远市行政区划图Fig.1 Administrative map of Qingyuan,Guangdong province

2014年5月22至23日，广东遭遇特大暴雨。重灾区清远市北部山区山洪暴发，南部低洼地区出现内涝。此次暴雨洪涝灾害的受灾人口约65万，受灾农作物50多万亩，倒塌房屋3300间，死亡5人失踪1人，给人民的生命财产安全造成了极大的威胁。针对此次暴雨洪涝事件，本文选择清远市作为实验区域，旨在根据本文所述方法在洪涝灾害发生的前期识别异常降雨并划分风险区，进而为灾害预警和救助提供指导信息。

1.2 实验数据

本文采用实验数据具体如下：

降雨数据：中国气象科学数据共享服务网发布的逐日网格降水量实时分析系统数据集，数据空间分辨率为0.25°×0.25°。

地形数据：地理空间数据云提供的ASTER GDEM数字高程数据，产品空间分辨率为30M。

河网数据：全国1:1 000 000的基础地理信息数据。

2 暴雨型洪涝灾害风险指数分析与计算

2.1 异常降雨因子

异常降雨是洪涝灾害发生的直接原因，在不同地区导致洪涝灾害发生的异常降雨的异常标准也不同。考虑到这种特点，本文以0.25°×0.25°作为空间分辨率将实验区划分，对各个区域分别构建时序分析模型ARMA，进而分析得到不同区域的正常降雨规律。

ARMA模型的基本思想是：将对象随着时间的推移而形成的序列视作为一组随机序列，然后用特定的数学模型来描述和逼近这个序列。这个模型一旦被识别且通过检验，就可以从时间序列的过去值来预测未来值。

ARMA(p，q)模型原理如公式（1），它表示当前预测值不但与之前自身P个滞后时间内的历史观测值有线性关系，还与过去q个滞后时间内发生的变化有关系。

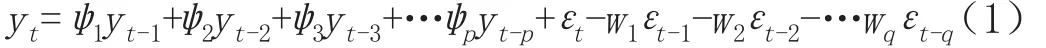
式中，p表示AR项的阶数、q表示MA项的阶数、t表示当前时刻、yt表示t时刻对象的值，即t时刻的降雨量大小、ψ为常数，表示自回归项的系数、是一组白噪声序列，它的均值为零，方差为σt2，代表与历史降雨数据不相关的其他影响因素、w为常数，表示移动平均项的系数[19]。

ARMA模型构建完毕之后可以预测接下来N步的正常降雨量上限。将实时降雨数据与正常降雨上限进行对比，并将两者之差作为异常降雨因子，划分其对洪涝灾害的影响度。对于每天评估的异常降雨因子R，采用表1值列确定其对洪涝灾害的影响度X1。其中，零值是降雨正常和降雨异常的分界线。异常降雨因子小于零说明实测值在预测范围内，降雨处于正常规律下，不存在洪涝风险；大于零说明实测值超出预测范围，认为出现异常降雨，并根据超出范围的程度划分异常降雨因子的影响度。实时降雨数据的接入实现了灾害发生前期异常降雨的识别，保证了暴雨型洪涝灾害风险分析的时效性。

表1 异常降雨因子对洪涝灾害的影响度计算表Tab.1 Eあect of abnormal rainfall factor on flood disaster

2.2 地形因子

地形对洪涝灾害的发生和发展有着重要的影响。首先，高程越低的地区越容易被淹没；其次，地形起伏越小的地区，洪水越不容易排泄出去，越有可能成为洪涝区域。根据实验区域的数字高程模型，可以直接得到高程信息，进而计算地形起伏度。对于高程因子H和地形起伏度因子S，借鉴前人的经验[20]确定它们对洪涝灾害的影响度X2和X3计算见表2和表3。

表2 高程因子对洪涝灾害的影响度计算表Tab.2 Eあect of evation factor on flood disaster

表3 地形起伏度因子对洪涝灾害的影响度计算表Tab.3 Eあect of terrain fluctuation factor on flood disaster

2.3 河网因子

河网的分布也影响洪涝灾害的发生和发展状况。从理论角度讲，距离河网越近的区域越容易受到洪水的影响，被淹没的可能性越大。借助GIS的空间分析能力，对河网建立多级缓冲区可以计算其对洪涝灾害的影响度。河流缓冲区L对洪涝灾害的影响度X4计算见表4[21]。

表4 河流缓冲区因子对洪涝灾害的影响度计算表Tab.4 Eあect of river network factor on flood disaster

2.4 构建暴雨型洪涝灾害风险指数

结合异常降雨、高程、地形起伏度和河网构建暴雨型洪涝灾害风险指数Z，其计算公式如式（2）所示。

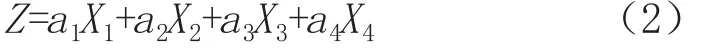
式中，X1、X2、X3、X4分别表示异常降雨因子、地形起伏度因子、高程因子和河流缓冲区对洪涝灾害的影响度，a1、a2、a3、a4分别代表各个因子的权重。

本文采用层次分析法（AHP）确定各个因子的权重。首先通过两两比较目标之间的相对重要程度构造判断矩阵，然后检验判断矩阵的一致性，如果不通过检验则需重新构造判断矩阵；通过检验则认为矩阵具有满意一致性，最后归一化得到各个目标对应的权重。

经过计算确定各个目标的权重分别为0.64、0.18、0.07和0.11，即暴雨型洪涝灾害风险指数计算公式如式（3）所示。

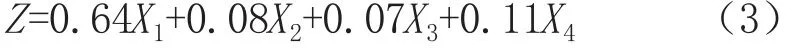
本文从异常降雨致灾的角度出发，认为异常降雨事件可以为洪涝灾害定性，即异常降雨导致暴雨型洪涝灾害发生。因此，本文将异常降雨因子R对暴雨型洪涝灾害影响度的分界点与其对应的权重0.64相乘得到的结果作为灾害风险等级的分界点，将暴雨型洪涝灾害划分为无风险、低风险、中风险、中高风险和高风险五级，等级划分表见表5。

表5 暴雨型洪涝灾害风险等级划分表Tab.5 Classification of risk levels of rainstorm-caused flood disaster

3 实验分析

3.1 异常降雨因子影响度计算

ARMA模型的适用条件包括：

1）输入数据在时间上必须是连续无间断；

2）输入数据必须超过60个，以保证分析结果的准确性。

本文从异常降雨致灾角度出发，旨在揭示正常降雨规律，即降雨未能致灾的规律。因此，在数据选择方面还需注意，在实验数据对应的时期内不能有暴雨型洪涝灾害发生，以保证规律的准确性。

综合以上三个约束条件，本文选择2014年3月1日至2014年5月20日的清远市范围内的逐日降雨数据作为ARMA模型的输入数据。

通过叠加逐日降雨栅格影像与清远市界，得到81幅栅格影像，其中每幅影像中包含28个栅格。本实验对此28个栅格逐一建模与分析，得到各个栅格包含的地区内的降雨规律，并进行六个滞后项的正常降雨量上限预测。在此基础上，以“日”为时间尺度，接入实测降雨量，对实测值和预测上限求差，差值图如图2所示。其中，降雨异常以水平零轴作为分界线。实测值与预测值之差大于零则说明实测值超出预测的正常降雨上限，此时认为降雨异常，存在发生洪涝灾害的危险；小于零则说明实测值在预测范围内，即降雨处于正常规律下，不存在发生洪涝灾害的危险。从时间角度来讲，5月22日和23日清远市大部分地区处于降雨异常中；从地区角度来讲，同一地区基本遵循洪涝风险在22日达到峰值，然后逐渐减小的规律，并且ID号从11号至22号所代表的地区降雨异常状况较为严重。将实测值与预测上限之差经过数据空间化并计算其对洪涝灾害的影响度，得到5月21日至5月26日的异常降雨因子的影响度等级如图3所示。从图中可以看出，5月22日清远市全部地区都处于降雨异常状态中；5月21日-23日期间，清远市中下部地区降雨异常情况比较严重；阳山县处于持续的降雨异常情况中。

图2 实测值与预测上限差值图Fig.2 Graph of diあerence between measured values and predicted maximum

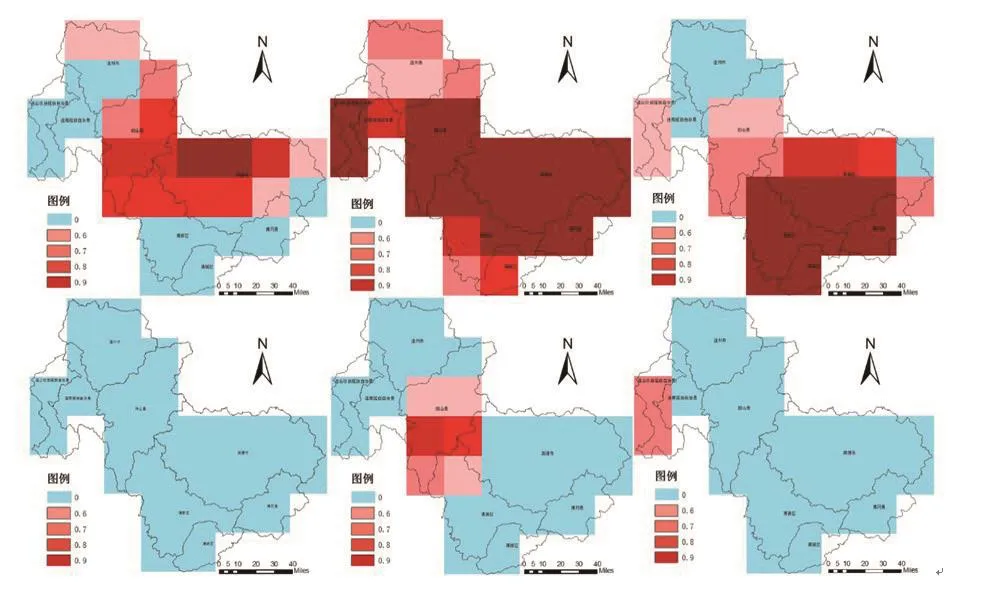
图3 广东省清远市异常降雨影响度等级图Fig.3 Eあect level of abnormal rainfall in Qingyuan,Guangdong province

3.2 地形因子影响度计算

由清远市30 m分辨率DEM得到高程因子的影响度分布如图4所示。通过GIS的栅格邻域分析方法，利用高程数据计算得到地形起伏度因子的影响度分布如图5所示。

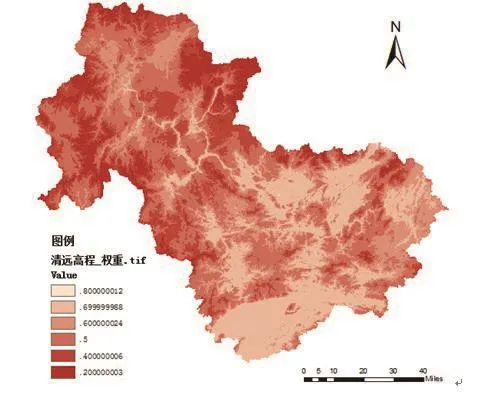
图4 广东省清远市高程影响度等级图Fig.4 Eあect level of evation in Qingyuan,Guangdong province

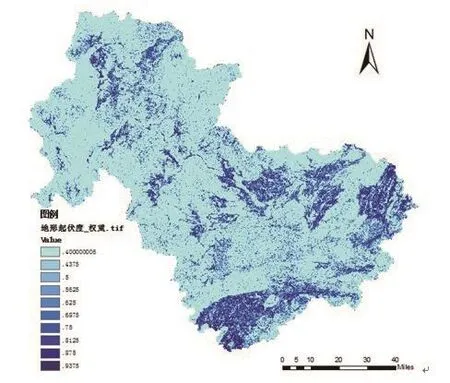
图5 广东省清远市地形起伏度影响度等级图Fig.5 Eあect level of terrain fluctuation in Qingyuan,Guangdong province

3.3 河网因子影响度计算

清远市境内仅有一条北江穿过，对其按照表4的标准生成多级缓冲区并确定影响度后，对洪涝灾害的影响度分布如图6所示。

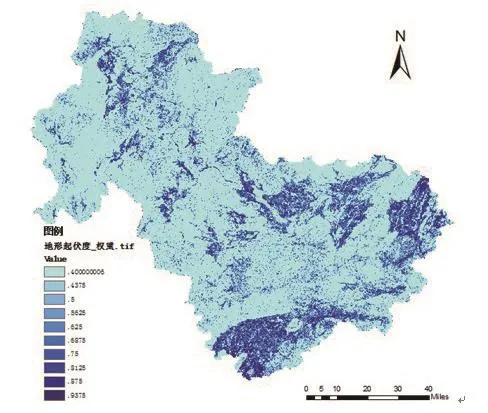
图6 广东省清远市河网影响度等级图Fig.6 Eあect level of river network in QingYuan,Guangdong province

3.4 暴雨型洪涝灾害风险指数计算与分析

将地形因子影响度分布图、河网因子影响度分布图与6天的异常降雨因子影响度分布图加权叠加，并按照表 5的标准为暴雨型洪涝灾害风险划分等级，得到2014年5月21日至2014年5月26日期间内每天的暴雨型洪涝灾害风险分布图，如图7所示。

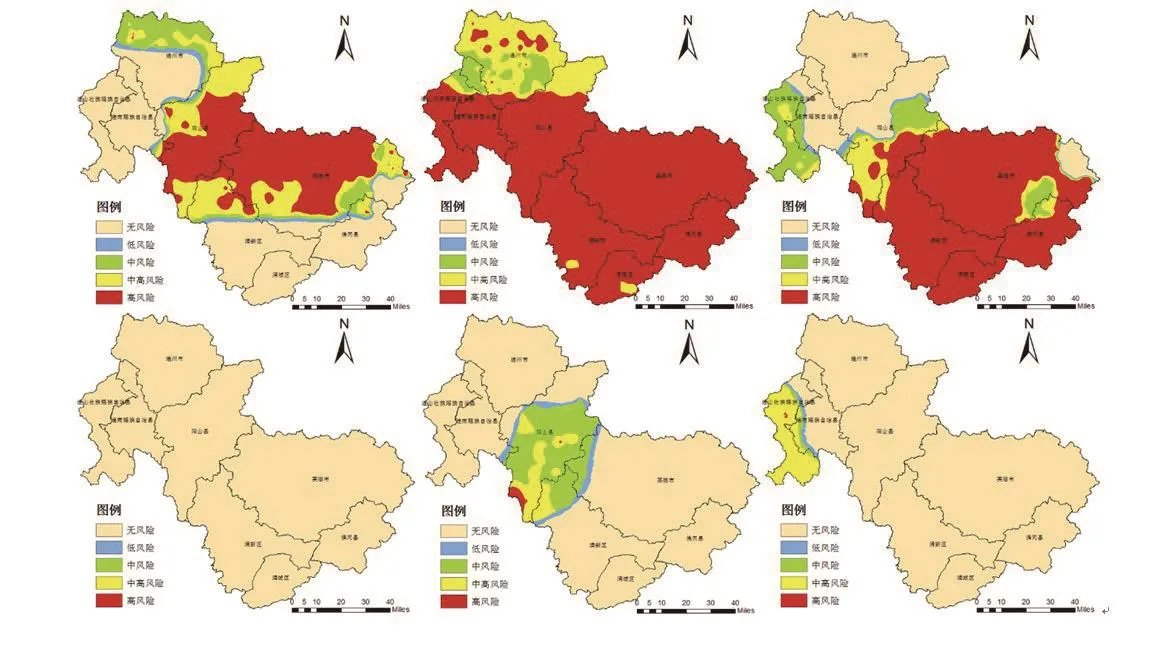
图7 广东省清远市暴雨型洪涝灾害风险分布图（2014年5月21日至2014年5月26日）Fig.7 Risk distribution of rainstorm-caused flood disaster of QingYuan,Guangdong province(May 21,2014-May 26,2014)

调查显示，在2014年5月22日至2014年5月24日期间，暴雨导致广东省清远市多地发生洪涝灾害。清远市北部发生山洪，南部发生内涝，其中阳山县灾情较为严重。截止5月26日，清远市阳山县3个村形成2.1 km2的积水面积。对照发现，5月21日至5月25日期间，阳山县中下部地区处于持续的较高暴雨洪涝风险中，说明预测的暴雨洪涝风险对于实际灾情有一定的预警效果。

4 结束语

本文从异常降雨致灾的角度出发，由不同地区的历史降雨数据分析得到该地的正常降雨规律，接入实测降雨数据来识别异常降雨，并将异常降雨因子与地形因子、河网因子结合，利用层次分析法构建暴雨型洪涝灾害风险指数。以2014年5月22日广东省清远市发生的洪涝灾害为例，在灾害发生的前期进行短时、高时效性的临灾风险分析，得到逐日灾害风险分布图，实验表明分析结果与实际洪涝灾情吻合较好，为近、短时洪涝灾害的发生和灾情的空间分布提供准确的参考信息。

基于实时降雨数据的暴雨洪涝灾害预警方法仍存在一定的缺陷，如历史降雨数据必须是连续并且期间无暴雨洪涝灾害发生的数据、降雨数据空间分辨率较低，影响风险分析结果的精度以及由于时序分析模型的限制，不适用于长期和灾害发生期间的风险分析。但是作为一种短时暴雨型洪涝灾害预警方法，本文使用的异常降雨计算方法使致灾因子的致灾性更具说服力，同时为短时、近期暴雨洪涝灾害的发生和空间分布提供了一种新的临灾预警思路。