变权栅格叠加方法研究——以生态敏感性评价为例

牛 强，揭 巧，李 县

(1.武汉大学 城市设计学院，湖北 武汉 430072；2.佛山市规划设计研究院，广东 佛山 528000；3.广西城乡规划设计院，广西 南宁 530022)

0 引 言

栅格数据叠加分析（Raster Overlay）是重要的空间分析方法之一，它是对两个以上栅格图层在空间位置上相对应的栅格像元值进行布尔逻辑运算、数学运算、求极值等，从而得到新的栅格图层的方法。其中加权栅格叠加是最常用的叠加分析方法之一，主要通过加权求和各栅格图层用来解决多准则空间决策问题，如选址、适宜性评价等（由于本文中的准则因子与栅格叠加图层所指对象相同，下文将这两个词汇等同使用）。加权叠加既能综合参与叠加的每个因子的属性，又能体现不同因子的重要程度，因此被广泛采用。

目前，加权栅格叠加方法中应用最广的是线性加权叠加法（Weighted Liner Combination，WLC），它为每个参与叠加的栅格图层按照其重要性赋予一个权重，叠加结果为在空间位置上相对应的各图层栅格像元值和权重乘积的总和。但在实际应用中，该方法无法控制叠加图层之间的抵销效应和相互干扰，并缺乏对非线性情况的考虑，往往带来综合结果的偏差。如Malczewski所举的选址分析例子[1]，如图1所示，叠加结果显示最好的地块位于右下角，该地块虽然在成本评价中得分极高，但同时在坡度评价中得分极低，假如两个因子的权重分别是0.6和0.4，根据WLC法该地块将得到研究区域的最高评分0.6，但该地块由于坡度问题显然是不适宜开发的，得分应趋近于0。该偏差是常权叠加方法难以解决的，因而许多学者对WLC方法提出疑议[1-4]。

图1 WLC叠加过程中的因子相互干扰Fig.1 Interference between factors in WLC

为了解决加权栅格叠加中图层之间的抵销问题，以及极值区域被埋没的问题，本文基于变权理论，提出了非线性的变权栅格叠加方法，通过它进行栅格叠加时，不仅能综合多个栅格图层的属性，还可以凸显叠加图层中个别极大、极小像元值的效应，弥补WLC综合时的抵消效应。最后以陶港镇生态敏感区评价为例进行了案例分析。

1 国内外研究现状及存在问题

栅格叠加的起源可以追溯到19世纪末20世纪初Charles Elliot and Warren Manning的光影叠加（sunprint overlay）和Jacqueline Tyrwhitt透明叠加（transparent overlay）。经McHarg的推广与实践，叠加方法成为了一种广泛应用的系统方法。McHarg使用透明的图纸，涂上不同明暗程度的阴影来表现其图层特性，最后叠置起来观察其总体效果[5]。这些方法统称为顺序叠加法（Ordinal Combination），是GIS空间叠加分析技术的原型。顺序叠加法在进行图层叠加时等同于数学中的加法运算，也就意味着默认了所有叠加图层的重要性相同，但实际情况并非如此。

为此，叠加方法引入了“权重”的概念，由此产生了线性加权叠加方法（WLC），它是GIS环境下使用最频繁的叠加方法[2，6-7]，其公式如下：

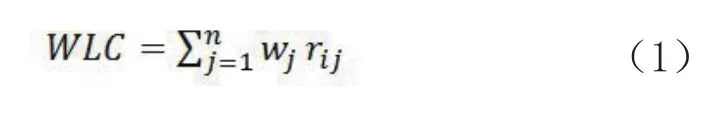
式中，wj是j因子的标准化权重，代表的是j因子的相对重要性，所有权重的总和为1，rij是i地点j因子的属性值，j因子所有地点的属性值构成一个叠加图层。

WLC法由于其原理简单、计算方便而被广泛应用，如生态环境评价[8]、用地适宜性评价[9]、设施选址分析[10]、土地利用动态趋势分析[11]等。

但是，WLC法有个重要的前提假设条件，就是因子之间的非相关性。但在实际运用中很难保证，导致在叠加中因子之间相互干扰和抵消，得到错误的分析结果，如图2所示的选址分析错误。

针对WLC法的上述问题，Hopkins提出了一些改进意见[2]，首先，在叠加因子的选取过程中可以通过统计分析等方法生成相对独立的因子；其次，在评价过程中，并非所有因素都是相互依赖的，对于可以凭经验或推演证明因子之间无相关性的特定情况下，使用线性叠加方法也是可取的。

而Jiang和Eastman则建议在叠加过程中采用位序加权平均法（Ordered Weighted Averaging，OWA）[4]。OWA法包括两套权重，评价因子的重要性权重及位序权重，其位序加权平均公式如下[3]：

式中zi1≥zi2≥…≥zin是将属性值xi1,xi2,…,xin按其大小降序排列的结果，wj是j因子的权重，vj是初始权重。

OWA是按照属性值xi1,xi2,…,xin的排列“次序”来确定其权重的，如有一组位序权重（0.5，0.3，0.2）和初始权重（0.1，0.3，0.6），按照位序法则来赋予权重给一组因子(A，B，C)时，如果这组因子属性值的降序排序为BAC，则OWA计算过程为（0.5×0.3×B+0.3×0.1×A+0.2×0.6×C）/（0.5×0.3+0.3×0.1+0.2×0.6）。Yager认为在OWA法中，因子的权重与它们的相对重要性及补偿方式是关联的，位序权重控制着叠加运算的过程，也就保证了抵消效应是可以被控制的，极值会得到额外的权重补偿[12]。

OWA法提出来之后，许多学者都将其应用到传统WLC法涉及的领域，并深入比较了两者的区别，如Malczewski等将OWA法用于Cedar Creek湿地的生态评价[3]，Romano等则将其用于意大利南部Piana di Macchia的用地适宜性评价[13]，他们通过比较都认为OWA法得到的结果比WLC法更加切合实际。但笔者认为OWA仍存在局限性，因子的权重按其位序分配，导致难以解释叠加结果的实际意义。

以上的叠加方法中权重都保持不变，都可以归为常权叠加方法，其优劣势总结见表1。常权叠加最常见的问题就是因子之间的抵消效应，它会使叠加结果趋于中间值，从而埋没一些重要的极值。

表1 常权叠加方法的优劣Tab.1 Compare of constant weight overlay methods

2 变权空间叠加方法

2.1 变权理论

常权叠加中权重的目的在于反映各准则因子的相对重要性，但当因子的组态（即各因素的取值状况）不同时，权重的恒定性导致综合结果不一定合理。例如，在做一项用地选址时，有两个考察因子，权重均为0.5，甲地的考察得分为90分和60分，乙地的考察得数为75分和75分，采用常权方法时两块用地的综合得分相同。而变权方法不仅考虑各因素的相对重要性，而且还考虑对因子组态均衡程度的偏好，如偏好极大值或极小值，能够更适应现实情况。上例中，如果更倾向于具有特别优势的用地，那么变权方法可以增加高得分因子的权重，使甲地胜出；如果更排斥具有特别劣势的用地，则可以增加低得分因子的权重，使甲得分更低，导致乙地胜出。

变权思想首先由汪培庄教授提出，强调因素权重应随因素状态值的变化而变化，以弥补常权决策带来的偏差[14]。李洪兴继而提出了变权原理及其公理化定义，并将变权类型分为3种：惩罚型变权、激励型变权和混合型变权[15-16]，并指出在现实中权重随状态水平变化的规律是千变万化的，应当根据具体情况确定变权公式。姚炳学、李洪兴进一步提出了局部变权的公理化定义，对不同的值域范围应用不同的状态变权函数[17]；李德清、李洪兴提出了离散度、调权水平等概念和方法，以分析变权力度[18]；李德清、郝飞龙对状态变权向量的变权效果进行了深入研究，提出了极点组态、权重变化率和均衡力的概念，试图为合理选择状态变权向量找到有效途径[19]。

2.2 变权栅格叠加

变权栅格叠加是变权理论在栅格叠加分析中的应用，对于叠加后生成的每个栅格像元，在确定其最终像元值时，对叠加图层中存在极大值或极小值的栅格像元的权重进行奖励或惩罚，即在既定各图层权重分配的基础上进行变权，从而达到既加权综合多个叠加图层的作用，又凸显个别极大、极小值栅格像元的效果。

变权栅格叠加包括惩罚型、激励型、混合型。采用惩罚型变权栅格叠加时，要求各叠加图层的栅格像元值都不能太低，强调参与叠加的各栅格像元值的均衡型，否则会因为惩罚数值过低的像元而使叠加得到的像元值更低。因而惩罚型变权栅格叠加方法主要运用于需要惩罚短板或缺点的评价情景，如建设用地适宜性评价中惩罚各单因子评价中得分特别低、特别不适宜建设的地段。激励型变权栅格叠加正好相反，会奖励高数值的像元而使叠加得到的像元值更高，因此它是奖励优点的变权方法。如下文的生态敏感性评价，各单因子评价中敏感性越高的地段，越需要重视和保护，类似的还有景观评价。激励型变权也常和惩罚型变权联合使用，即混合型变权，达到既惩罚短板，也奖励优点的效果,从而使叠加结果更具有离散性，便于划分等级，常用于地质环境评价，选址评估。

针对变权栅格叠加，其叠加过程为如图2所示。假设对于某一栅格叠加分析，存在n个准则因子的叠加图层，各因子的原始权重向量为W，首先构造某种状态变权函数，并据此求得各图层的每个栅格像元的状态变权值（即调权幅度）S(X)，然后对各个栅格像元的状态变权值和原始权重值的乘积进行归一化处理，得到各个栅格像元的变权权重W(X)，最后将所有叠加图层的各个栅格像元值和变权权重进行加权求和，得到叠加后的栅格像元值M。其中涉及到状态变权函数、归一化函数和变权综合公式，分别解释如下：

图2 变权栅格叠加过程Fig.2 Process of variable weight raster overlay

1）状态变权函数

状态变权函数主要用于确定状态变权向量S(X)，即权重的变化幅度。它主要根据参与叠加的像元值的状态来设定调权幅度。以图2为例，叠加图层为A、B、C，每一个栅格像元针对这3个图层都有1个像元值，从而形成了许多组状态向量，如左上角红色栅格像元的{9，5，3}和白色栅格像元的{3，5，9}。采用局部激励型变权，当任意图层的栅格像元值＞7时，相应权重翻倍，即200%调权幅度；当像元值≤7时，权重保持不变，即100%调权幅度。那么对于红色像元，A图层的像元值超过7，其他图层的像元值都未超过7，因而其状态变权向量为 {200%，100%，100%}，即{2，1，1}，对于白色像元，C图层的像元值超过7，其他图层都未超过7，因而其状态变权向量为{1，1，2}。

目前，比较常见的状态变权函数主要有经验公式、非标准指数函数、指数函数，但除了指数函数可用于激励型变权外，其他函数多用于惩罚型变权，各状态变权函数如下：

①经验公式

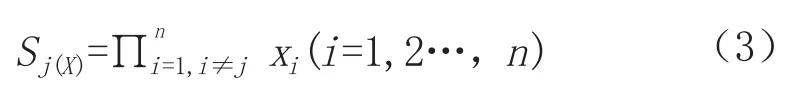
式中，xi为i因子评价值标准化处理后的小数，Sj(X)表示除了xj之外的所有xi值相乘所得的值。若因子本身值越小时，则自身S(X)值相对越大，为惩罚性变权公式，变权结果会让权重过多的集中到最小状态值的因子上，效果较为极端。

②非标准指数函数

式中，xj为j因子评价值标准化处理后的小数，当α〈0时，可作为惩罚型变权，当α〉0时，可作为激励型变权，但变权效果同样较为极端。

③指数型状态变权向量

该类型函数既可以用于惩罚型变权，又可以用于激励型变权，且变权力度可调节性较强，变权结果不会过于极端。已成为学者们研究的重要方向，并将重点放在如何根据需要确定一个合理的α值上，是目前较为有效的方法。

2）归一化函数

将通过原始权重W和状态变权向量S(X)的归一化的Hadamard乘积来得到变权权重W(X)。

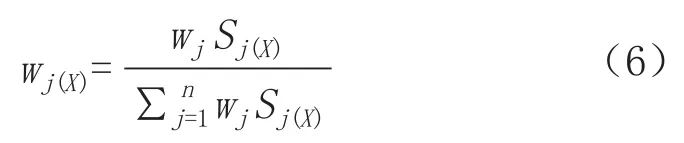
式中，wj(X)为变权后第j个因子的权重；wj为第j个因子的原始权重； S(X)=(S1(X)， S2(X)，…， Sn(X))为状态变权向量。

因此图2中两组栅格像元的原始权重{0.5，0.3，0.2}经过变权后变成了{0.67，0.2，0.13}、{0.42，0.25，0.33}。

3）变权综合公式

完成变权后，综合叠加与常权总和方法相同，即为各叠加栅格像元值与变权权重乘积的总和，

式中，M为叠加得到的某个栅格的像元值；n为叠加图层个数；wj(X)为变权后j图层参与该叠加的栅格的权重；xj为j图层参与该叠加的栅格的像元值。对于图2，以红色栅格为例，其评价值计算式为0.67×9+0.2×5+0.13×3=8.13，相对于常权叠加的6.6，其重要性得到了提升。

3 案例研究

3.1 研究简介

研究选择紧邻湖北网湖湿地省级自然保护区的陶港镇区作为变权叠加方法的实验对象，研究区面积为11.8km2。该镇山水资源丰富，属于生态本底良好的湖滨小镇，研究区域北部为大片农田，东、南两面邻网湖，湖叉呈触角状深入镇区腹地形成大片湿地，与山林小丘相互交织，形成多样化的湖峡地貌，构成宜人的山、水、田格局。在城镇化的大趋势下，网湖湿地面临城镇用地扩张的较大压力，因此，本文基于变权叠加的生态敏感性评价方法，判别出需要控制和保护的生态敏感区，以更好地保护网湖湿地。

本案例的生态敏感性评价大致包括指标体系的构建、单指标因子评价和多指标因子叠加综合3个环节。在指标体系构建环节，会筛选出生态敏感性的评价因子并确定各个因子的权重。然后在单指标因子评价环节，会针对每个指标因子，对研究区域的各个地段进行敏感性分区、定级，得到单因子评价栅格图。最后在多指标因子叠加综合环节，对所有单因子的评价结果进行加权栅格叠加，得到各个地段的生态敏感综合评价值，并以此作为主要依据来划分生态敏感区。其中，研究将采用本文提出的变权栅格叠加方法来进行多指标因子综合，结合传统的常权栅格叠加结果，对比分析本方法的科学性和有效性。

3.2 变权叠加方法

在生态敏感性评价中，有些关键因子在达到一定敏感级别后，由于非线性的木桶效应，会给综合生态敏感性带来极大影响，是严重生态问题的可能触发点。基于这种考虑，本文采用局部激励型变权模型，对于突破一定敏感级别（如评价值为高度敏感或极度敏感）的关键生态因子，通过动态增加其权重来达到保证其优先度的目的。而权重改变幅度由状态变权函数决定，本文采用指数函数作为状态变权函数，具体公式如下：

1）局部激励型状态变权函数

本文只对关键生态因子进行变权（下文称之为变权因子），并且只对超过一定敏感级别的评价单元进行局部激励变权，开始变权的敏感级别对应的量化数值称为变权阈值。状态变权函数如式（8）。

式中， Xj为第j个因子的状态值；α为变权力度，且α〉0，α越大，变权幅度越大；βj为第j个因子的变权阈值；I是变权因子的集合。

2）变权力度控制

为得到适合的变权力度α，本文参考李德清等的研究成果[19]，引入极点组态最大变权倍率Δ的概念。Δ是指极点组态下（即一半因子为最大状态值，另一半为最小状态值的一组状态向量）权重最小的变权因子的最大变权倍率。经过推导，得出Δ与变权力度α之间具有式（9）所示函数关系，因而可以通过设定具有实际含义的最大变权倍率Δ，来求解合适的α值。

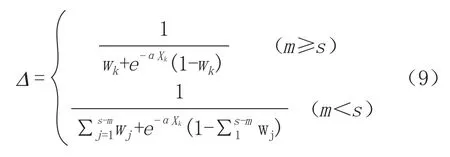
式中，m为非变权因子个数，wk为变权因子中最小权重值，Xk为最大状态向量。对变权因子按权重大小进行排序：w1≤…≤w(s-m)≤…≤w(n-m)，n为因子总个数；上式中，当n为偶数时，s=n…2；当n为奇数时，s=((n-1))/2。在确定Δ时需保证式（9）有意义，即m≥s时，， m〈s时，)。

为了确定合适的极点组态最大变权倍率Δ，本文采用最大信息量法。即在上述Δ取值范围内，按照一定的步长求得所有Δ对应的变权公式，并求得各自的变权叠加结果，计算各变权叠加结果的信息量，取信息量最大的叠加结果为最优变权结果，进而得到合适的Δ和α。

3.3 指标选取

根据陶港镇区生态环境特征，确定包含8个生态因子的指标体系，并采用层次分析法和德尔菲法确定因子基础权重，具体见表2。研究区域属于丘陵和湿地地形的混合地带，山水元素是其重要生态保护要素，相关因子多为变权因子，而坡向因子影响相对较小，定为非变权因子。

表2 陶港镇生态敏感区变权评价指标体系Tab.2 Index system of ecological sensitivity evaluation of Taogang town

3.4 综合评价

1）单因子评价

根据表2所列评价标准，以5m×5m栅格像元作为基本空间单元，采用GIS技术对研究区域进行各个因子的敏感度评价。评价等级分为5级，分别用分值1、3、5、7、9代表不敏感、轻度敏感、中度敏感、高度敏感、极度敏感。得到栅格数据格式的单因子评价结果如图3所示。

2）变权叠加

首先求得使式（9）有意义的Δ的取值范围为[0，4]，由于研究区域生态环境相对比较敏感，因此尽量选择较高的最大变权倍率Δ，所以从2开始按0.25步长设置Δ，带入式（9）求得系列α值，带入式（8）得到系列变权叠加公式。

然后，利用每个变权叠加公式，对这8个单生态因子评价结果进行变权栅格叠加。由于计算量非常大，我们在ArcGIS下用Model Builder开发了相应的工具以批量完成上述工作。最后利用信息量法，分析不同Δ下的叠加结果，找出信息量最大的那个作为最佳变权叠加结果，它对应的Δ为2.75，α值为2.39。

图3 单因子评价结果Fig.3 Evaluation results of single factor

上述叠加得到的像元值是位于连续区间[1，9]中的任意数值，因而需要在保证标准分值含义不变的前提下（如1代表不敏感，3代表轻度敏感），明确标准分值之间的其他评价值的含义（如2代表不敏感）。为此，本文根据等分法将综合评价值区间[1，9]等分为5段，每段跨度为1.6，由此得到以下敏感度分区：1≤不敏感≤2.6；2.6＜轻度敏感≤4.2；4.2＜中度敏感≤5.8；5.8＜高度敏感≤7.4；7.4＜极度敏感≤9。据此得到变权叠加结果如图4所示。

图4 变权综合评价结果Fig.4 Result of variable weight raster overlay

3.5 叠加结果分析

1）整体分析

如果采用目前通常使用的常权叠加方法，将得到如图5所示的常权叠加结果，两者的对比见表3。从图5和表3中可以看到常权叠加结果没有极度敏感的区域，只有少量高度敏感的区域，占总研究区域的21%。由此可见抵消效应带来的巨大影响。而变权叠加结果中存在大量极度敏感区域，占37%；高度敏感和极度敏感区域占总研究区域49%，其面积是常权综合评价的2倍。

图5 常权综合评价结果Fig.5 Result of constant weight raster overlay

两个评价结果中，差异最为明显的是位于中北部、从东向西深入研究区域的湿地，尽管在多个单因子评价中被评为极度敏感，但常权叠加结果却降为中度敏感和轻度敏感，与实际情况不符。由此可见，常权叠加会抵消掉大量极度敏感区域，会影响到城镇生态敏感区划定的合理性。

表3 变权叠加和常权叠加的各个敏感等级用地占比分析Tab.3 Land proportion analysis of each sensitivity level with variable weight overlay and constant weight overlay

2）局部采样点分析

本文选取3个具有代表性的评价基本单元分析变权叠加的效果，采样点位置如图4所示，其权重的变化见表4。

表4 采样点权重变化Tab.4 Weight changes of sample points

采样点A是镇区内最高山峰的南坡，状态值在高程和坡向方面表现为极敏感，但根据表2中的变权评价指标体系，只需对高程因子进行变权，由于其常权较小，且为唯一变权因子，导致最大变权倍率超出之前设定的Δ，为4.9倍，其他因子权重相应减少，变权叠加结果为5.62，即中度敏感，与主观判断相一致，因为该处无论是从生态角度还是从环境景观角度都是需要进行保护的地段。如果采用常权叠加，A处的叠加结果只能达到轻度敏感的级别。

采样点B处于湿地风貌区。该点在栖息地类型和物种丰度方面表现较为极度敏感，超过变权阈值，这两个因子变权后的权重为常权的2.5倍。如果采用常权叠加，评价值只能得到中度敏感，远低于主观判断。变权叠加将该处的评价值提升到极度敏感，更为合理。

采样点C位于南部湖区，在水域、栖息地类型、物种丰度、洪水风险4个方面表现为极度敏感或高度敏感，均超过变权阈值。由于需要变权的因子数较多，且存在总权重为1的限制，因此不可能都大幅度变权。这4个因子的变权倍率分别为1.8、1.1、1.75、1.07，其中，单因子评价值越高，变权倍率越大。而其余的4个因子——高程、坡度、坡向和归一化植被指数，由于它们没有参与变权，因此其权重被大幅度缩减至0.02以下，它们对评价结果的影响几乎减少为零。而这是与主观判断相一致的，因为这些因子对于水域的敏感性评价而言影响很小。相对于常权叠加的高度敏感的结果，变权综合得到了极度敏感的结果。

由此可见，较之常权栅格叠加，变权栅格叠加既能反映各叠加图层的综合作用，又能凸显极值的重要性，可使生态敏感性评价的结果更为合理。

4 结束语

本文对加权栅格叠加方法进行了较全面的回顾，并对常权栅格叠加方法的优劣进行了比较，指出常权叠加存在的逻辑规则过于简单、极值像元被抵消等问题。针对这些不足，本文基于变权理论提出了变权栅格叠加方法，以及相关模型，该方法不仅可以达到加权综合的效果，还可以对叠加图层中存在极大值或极小值的栅格像元的权重进行奖励或惩罚，从而保留重要的极值像元的效应，控制叠加过程中的抵消效应，可以适用于用地选址、生态敏感性评价、用地适宜性评价、景观环境评价、地质环境评价等。最后，本文以陶港镇生态敏感分析为例，利用局部激励型状态变权方法，对该方法进行了实践检验。从叠加结果来看，本文所提出的方法相较于常权叠加方法更为合理，更为准确地识别出了生态敏感区域，验证了该方法的有效性。尽管如此，该方法还需要在更多的实践中去进一步完善，特别是变权力度α的设定还需要通过大量实践来找到合理取值区间。