电动汽车接入电网多目标交易研究

张 雯，李 凯，王 男，于千千，邓少治

（国网山东省电力公司经济技术研究院，山东 济南 250021）

电动汽车接入电网多目标交易研究

张 雯，李 凯，王 男，于千千，邓少治

（国网山东省电力公司经济技术研究院，山东 济南 250021）

随着我国电动汽车产业的不断发展，关于电动汽车接入电网的研究日益增多，但多数只考虑了单一目标，如经济效益最优或环保效益最优。提出电动汽车接入下的电网多目标交易；考虑电动汽车的V2G特性，得到其充电功率；从单目标研究入手，分别建立以排量和价格为单目标的函数，得到最优解。进一步构建多目标函数，将购电费用和排放量转化为隶属度函数（单目标），最终得到兼顾双方、经济效益和环保效益折中后的最优解，对大规模电动汽车接入后电网的运行调度起到一定的辅助决策作用。

电动汽车；V2G；单目标函数；多目标交易

Abstract:The electric vehicle industry develops rapidly in China in recent years.However，the current grid trade research，using single objective model as the main research instrument，could not equilibrate the collective effect to the grid when various factors are taken into consideration，such as power purchase price，emissions，etc.Based on this situation，we propose the multiobjective optimization transaction research of the grid under the EV access.Firstly，the EV charging power result is obtained considering its V2G characteristic.Starting with the single objective model，the optimum solutions for the single objective evaluation of electricity costs and charging emissions are acquired separately.Then，the multi-objective optimization is carried out，which can take both the electricity cost and charging emissions optimizations into considered.The proposed evaluation method would make positive contribution to the power grid dispatching.

Key words:electric vehicle；V2G；single objective function；multi-objective optimization transaction

0 引言

电动汽车既可以通过电网充电，也可以在电网负荷处于较低水平时向电网供电，这种双向通信称为V2G （Vehicle-to-Grid），V2G技术是智能电网技术的重要组成部分。近年来，我国电动汽车产业发展迅猛，电网交易研究以单目标研究为主，但无法均衡购电费用、排放量等多个因素共同作用时对电网交易的影响。因此，在大规模电动汽车接入后，如何准确地预测V2G在电网调度过程中需要的各种参数将成为电网运行调度重点关注的问题。从电动汽车的V2G特性入手，通过在负荷高峰时向电网供电，负荷低谷时充电，起到一定的削峰填谷作用。首先对电动汽车进行负荷预测，并根据其V2G特性，利用粒子群优化法进行负荷计算，得到充电功率，进一步，分别确立以排量和价格为单目标的函数，得到最优解。在此基础上，构建起多目标函数，将购电费用和排放量转化为隶属度函数（单目标），引入模糊化工具，并采用内点法运算，使隶属度系数λ最接近于1求出最优折中解，即可得到兼顾经济效益和环保效益的最优解。

1 电动汽车充放电计算

在电动汽车V2G特性下，将电动汽车整体视作控制中心，研究接入后对电网负荷的影响，即在已知实际区域负荷曲线下，求出电动汽车的充放电时间和充放电功率，从而改善负荷曲线。由于电动汽车数量较多，并且每辆电动车的可用时间、电池初始容量、充放电功率限制和用户设置的电池容量最低限值均不相同，因此选择原理简单且受优化问题维数的影响较小的粒子群优化算法［1］（Particle Swarm Optimization，PSO）。

电动汽车实现区域负荷响应的控制策略应以尽可能拉平负荷曲线为优化目标，采用PSO算法优化每一辆电动汽车每一时段与电网之间的交换功率。此优化问题中粒子维数为24n，n为车辆数，可见粒子维数是随着电动汽车数量变化而变化的。粒子I的位置为

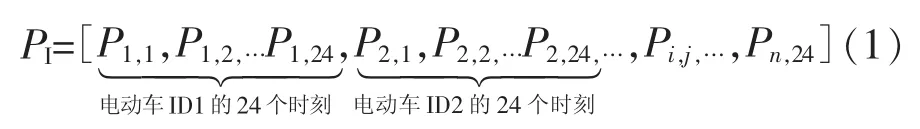
式中：ID1为电动汽车标志号。

1.1 确定目标函数

将电动汽车控制中心作为负荷计算整体，将1天分为24个时间段，以每辆车在每个时间段的充放电功率为变量，以负荷曲线的均方差最小为目标函数［2］，即

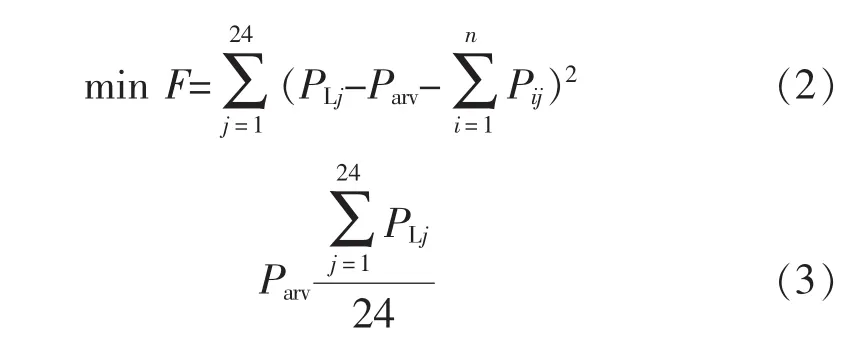
式中：n为电动汽车辆数；Pij为电动汽车i在j时段与电网的交换功率 （正值为放电，负值为充电）；PLj为j时段的负荷功率。

随着电动汽车数目的增加，电网调度对电动汽车控制中心的功率命令可以是充放电计划，以完成功率计划为目标制定电动汽车充放电策略，目标函数为

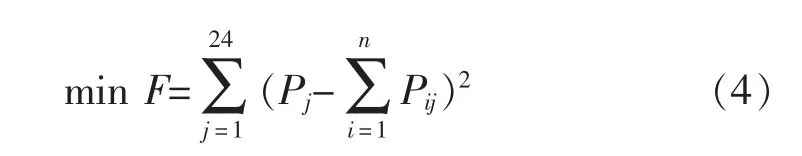
式中：Pj为电动汽车控制中心接受到来自电网调度充放电计划对应j时刻的功率。

1.2 确定约束条件

电动汽车参与电网互动受到约束条件主要为可用时间、充放电功率、电池可用容量及用户设置的最低 SOC（最低电池容量）4 个方面［3］。

1.2.1 功率约束

功率约束主要体现在充放电电流和充电线路功率容量的约束，充电电流最大值放电电流最大值2IiN。

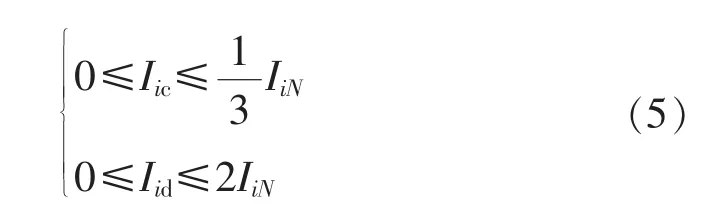
根据220 V接入时充换电设施单相负荷不超过10 kW，考虑线路功率容量约束，可按照不超过15 kW计算：

综合式（4）（5）可得：

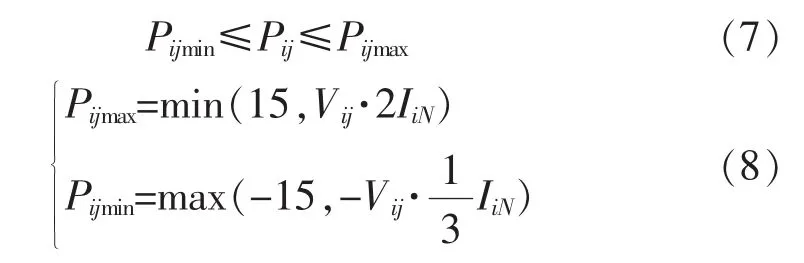
式中：Iic为电动汽车i的充电电流值；Iid为电动汽车i的放电电流值；IiN决定于电动汽车电池型号，80 Ah的电池对应此值为80 A；Vij为由电池充放电曲线得到的实时电压值；Pij为电动汽车i在j时段时充（放）电功率，正（负）值表示电动汽车处于充（放）电状态；Pijmin为电动汽车i在j时段时充（放）电功率下限；Pijmax为电动汽车i在j时段时充（放）电功率上限。

1.2.2 能量约束

电动汽车电池的容量是一定的，实际容量（QN）是指在一定的放电条件下，电池从充满电状态放电至放电终止过程中的放电容量。电池的容量不能超过实际容量值，考虑电池寿命容量不低于电池容量的20%。

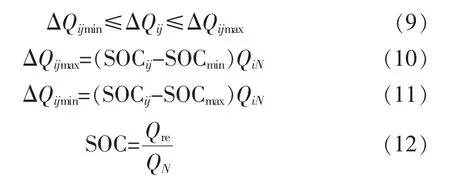
式中：SOC为电池实时容量值，即电池剩余容量与最大容量的比值；SOCij为电动汽车i在时刻j的实时容量状态；SOCmin为考虑电池自身约束时最低值，SOC取 0.2；SOCmax为 SOC最大值，取 1；QN为电动汽车的实际容量值，Ah；Qre为电动汽车i在 j时段的电池剩余容量，Ah；ΔQij为电动汽车i在时段j的充（放）电容量；ΔQijmin为电动汽车i在时段j的可用容量下限；ΔQijmax为电动汽车i在时段 j的可用容量上限。

1.2.3 可用时间约束

由于电动汽车不可能24 h都处于连网状态，因此当电动汽车非联网时其可用功率为零。

1.2.4 用户设置出站时最低电池容量

每个用户可以设置车辆离开时的最低电池容量，考虑实现用户的行程需求电量，又有如下约束条件：

式中：SOCi，set为车辆 i出站时的最低 SOC （用户设置）；k为电动汽车出站时刻。

设定某地区的电动汽车保有量为600万辆。根据某地的实地调研数据显示，在已知实际区域负荷的情况下，将实际区域负荷与电动汽车负荷相加，视作系统负荷。考虑多种电动汽车充电行为，在1 d内划分为24 h，并对系统负荷进行预测。表中负值代表放电，正值代表充电。系统负荷如表1所示，图1为其折线图；电动汽车负荷如表2所示，图2为其折线图。

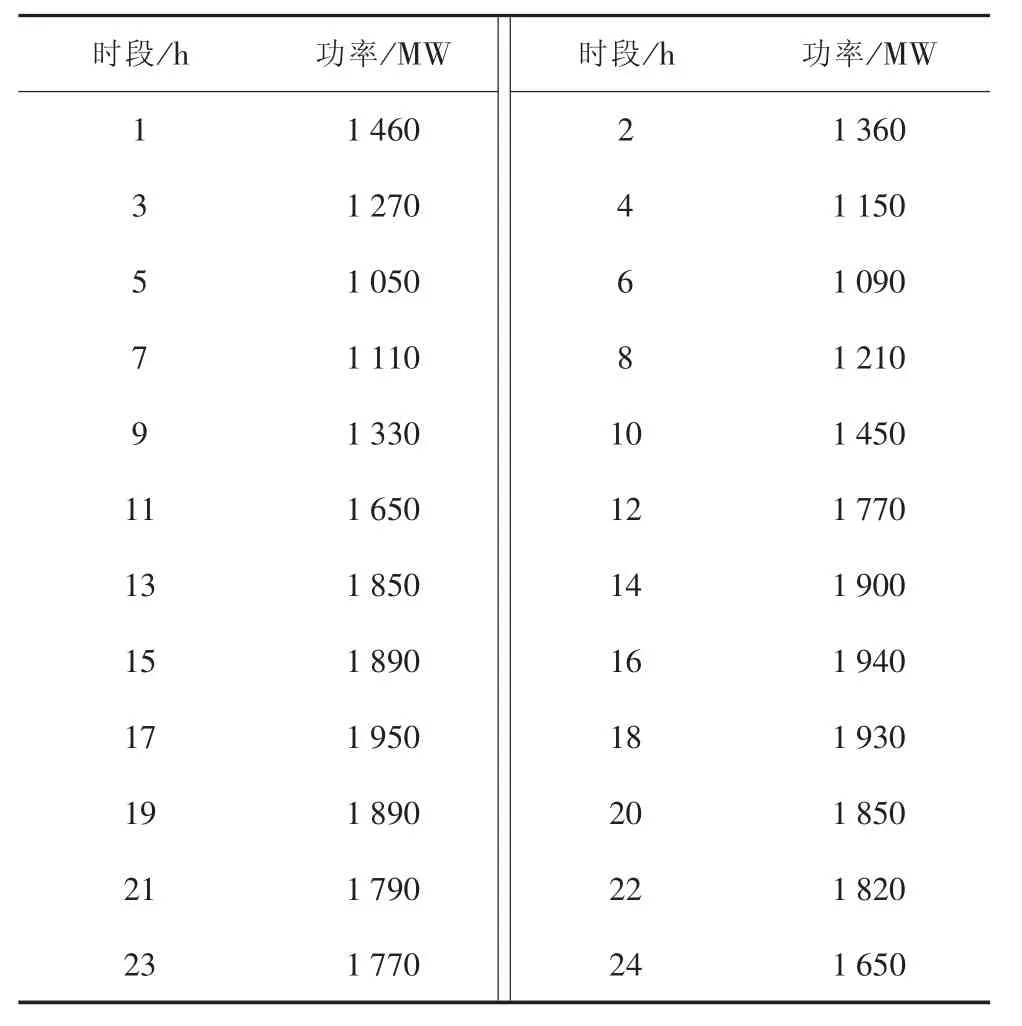
表1 系统负荷24 h日功率负荷预测数据

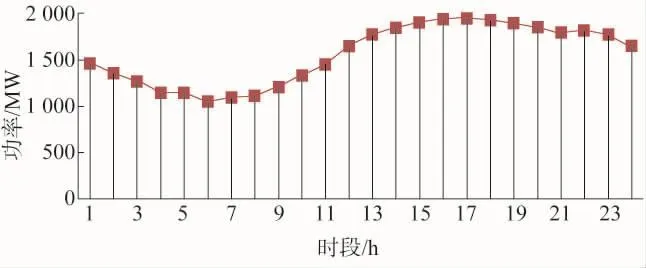
图1 系统负荷24 h日功率负荷预测曲线

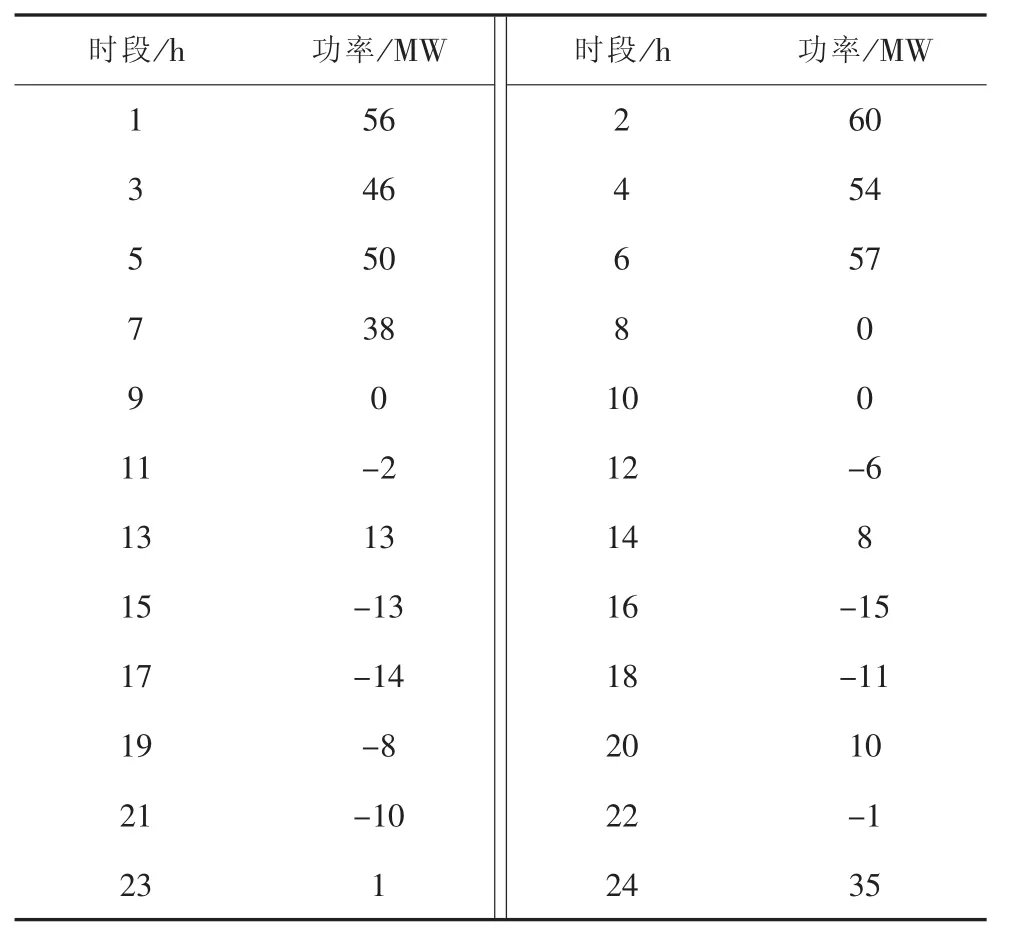
表2 电动汽车24h日功率负荷预测数据

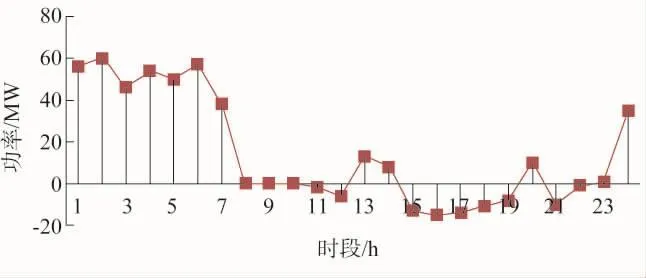
图2 电动汽车24 h日功率负荷预测曲线

2 电动汽车接入下的电网单目标交易

在已知电动汽车24 h负荷大小后，通过设计目标函数和适应度函数，根据适应度大小进行遗传、变异的计算。假定每组个体有4组解，即将系统负荷等效为4组发电机出力，先形成初始解 （假设有20组），求出适应度值。通过Matlab中遗传算子得到最终的20组适应度函数值最大即为最优解，也就是单目标最优解。

2.1 购电费用单目标模型建立

购电费用最小的目标函数［4］：

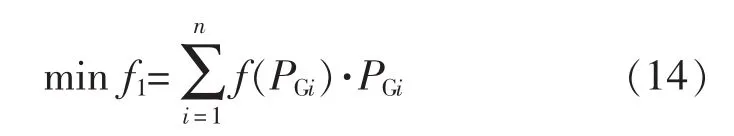
式中： f（PGi）为有功报价；对 f（PGi）=apiPGi+bpi，其中 PGi为机组有功出力，且为一次上升型。以上函数均化为标幺值计算。

这4个机组对应电动汽车负荷模型的单目标函数约束条件。

系统功率平衡约束为：

系统功率备用约束为：

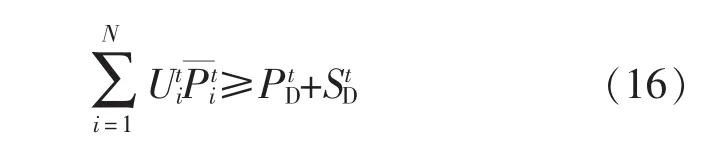
机组输出功率约束为：

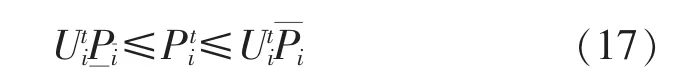
适应度函数为［5］

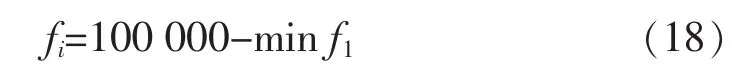
假设在Matlab算子中，遗传算法的运算次数N设定为100次，则最终会得到20组数据，每组数据均是矩阵，每一列分别代表4×1组发电机的出力。代入适应度函数计算，可得其最大值。根据算例可假设一个适应度值f0，求fi出f0和的差值，若有：

式中：ε为一个极小值，则满足适应度，即所求解为最优解。

通过Matlab算子仿真分析后可得以购电费用为单目标的最优解数据如表3所示。购电费用最小函数曲线见图3。

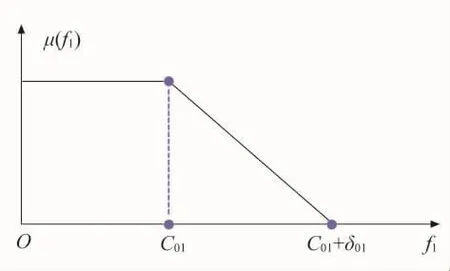
图3 购电费用最小函数曲线

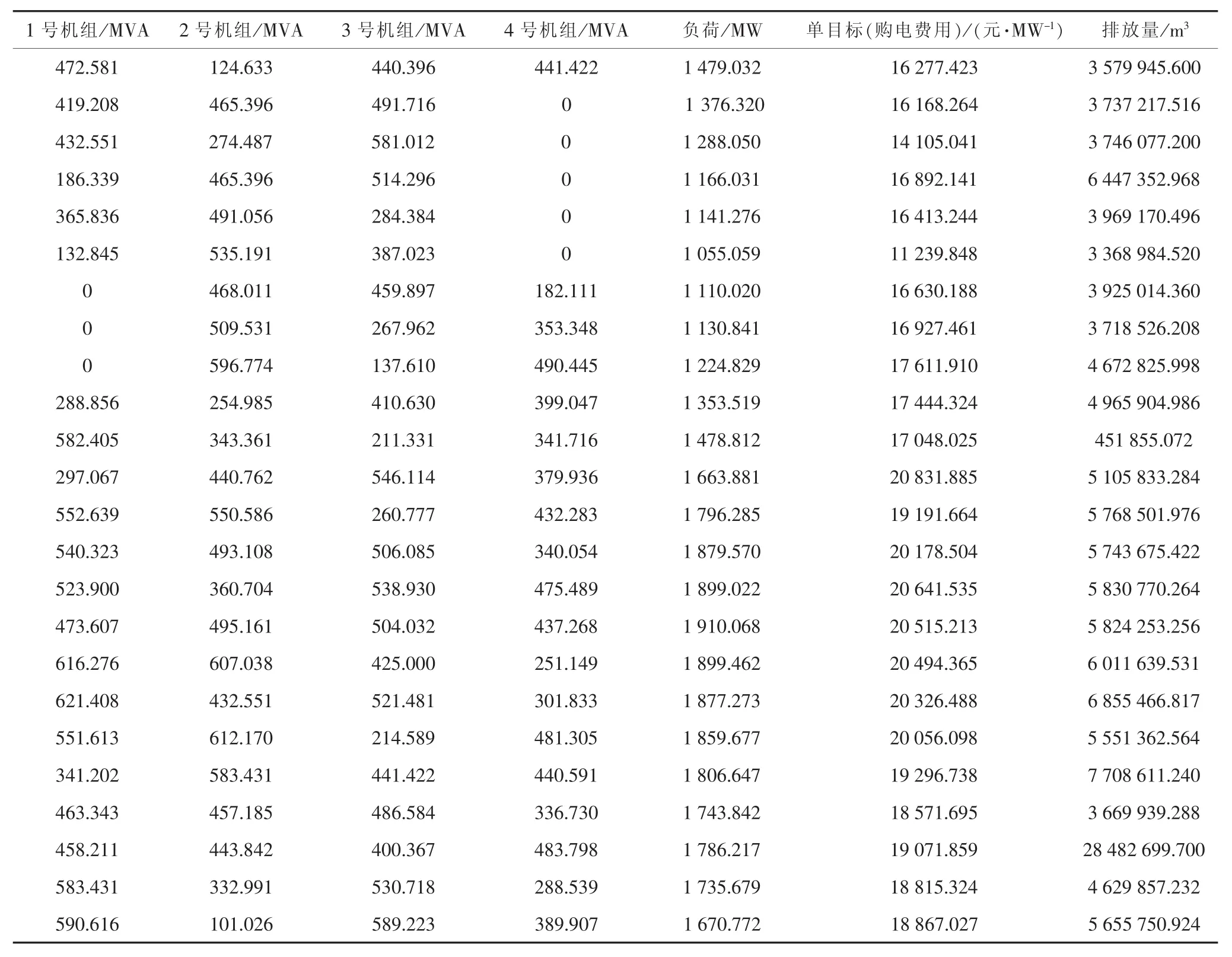
表3 以购电费用为单目标最优解

2.2 排放量单目标模型建立

排放量目标函数［6］为

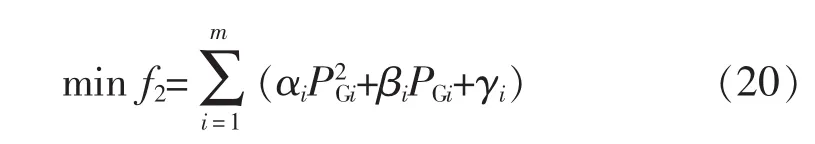
式中：α、β、γ为机组 i的污染排放系数；PGi为机组的有功出力。

4个机组对应电动汽车负荷模型的单目标函数约束条件。

系统功率平衡约束为：

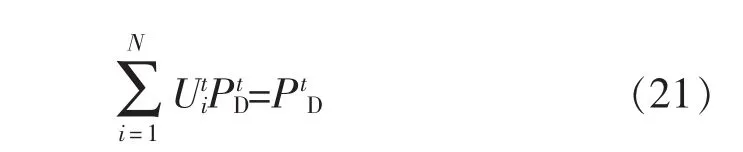
系统功率备用约束为：

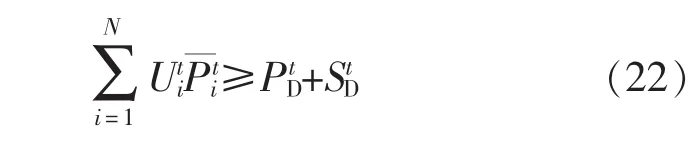
机组输出功率约束为：

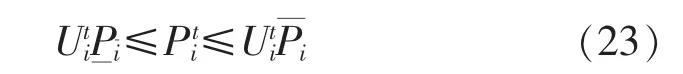
适应度函数为

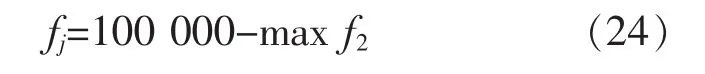
以上计算均化为标幺值后再转化为有名值计算适应度函数求最大值。同理若有：

则为最优解。

通过Matlab算子仿真得到以排放量为单目标的最优解数据如表4所示。排放量最小函数曲线见图4。

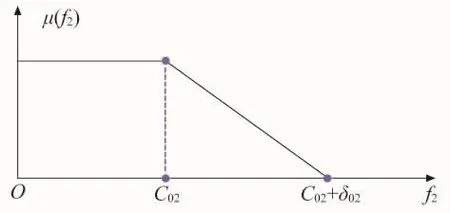
图4 排放量最小函数曲线

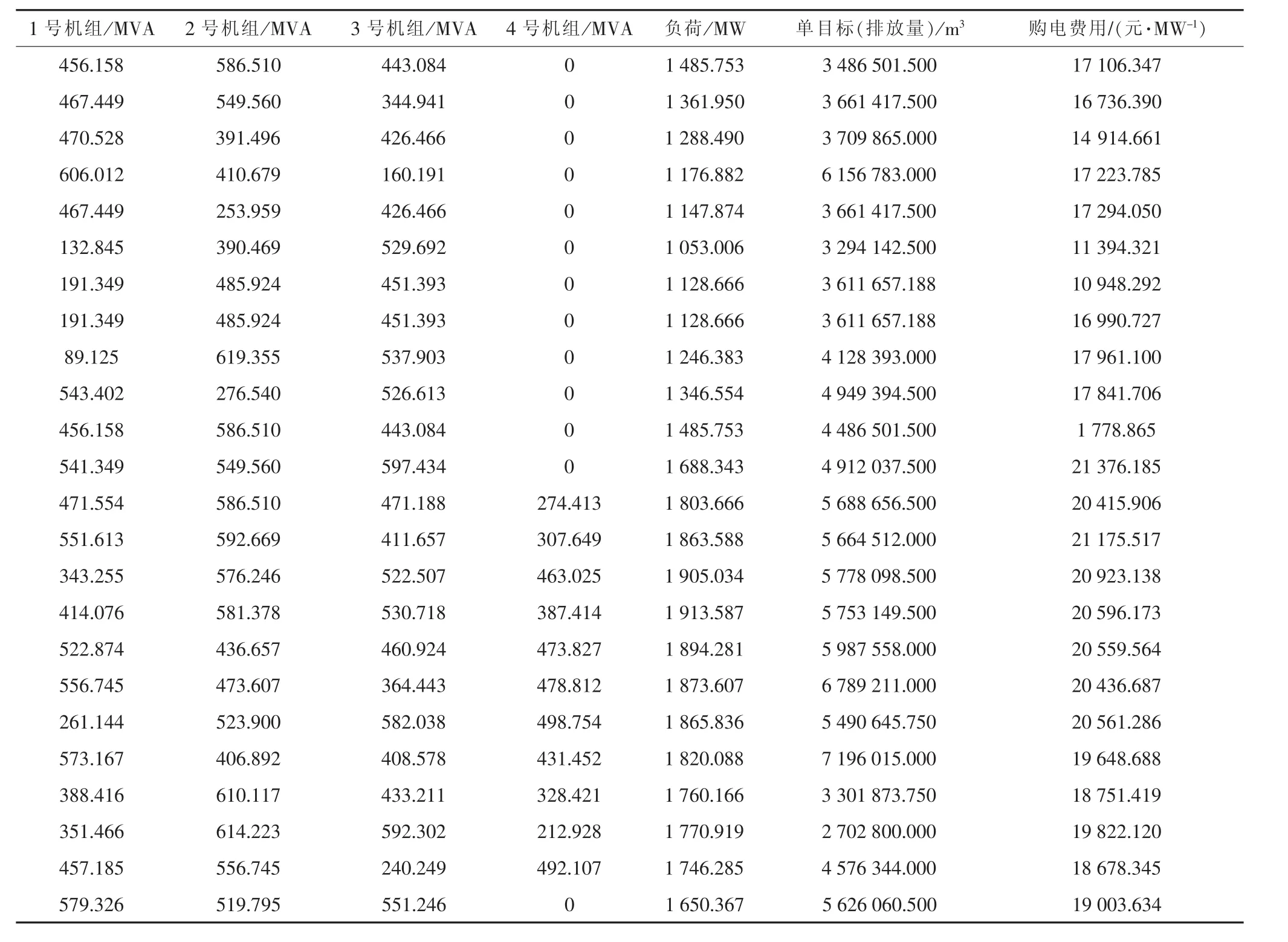
表4 以排放量为单目标的最优解

机组参数如表5所示，电价参数如表6所示，排放系数如表7所示。

表5 机组参数

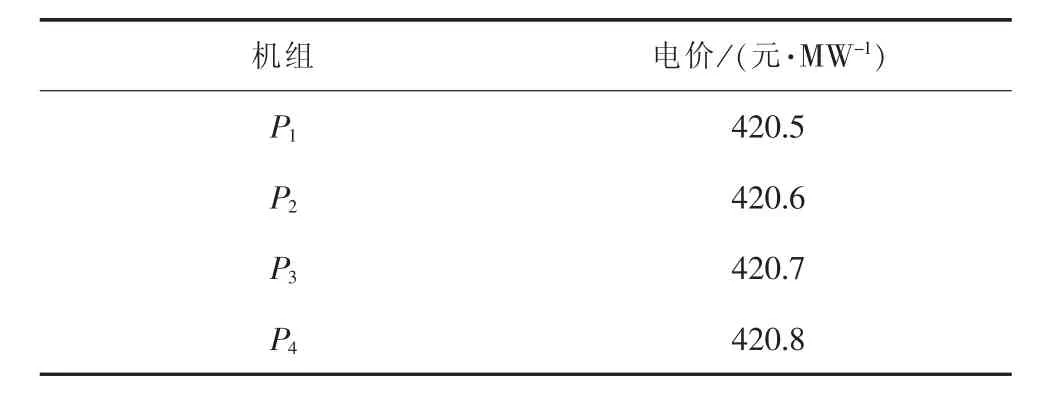
表6 电价参数

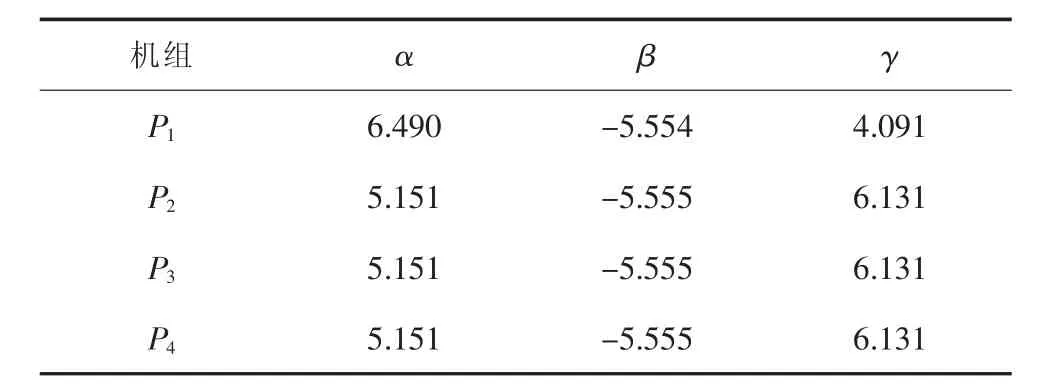
表7 排放系数

3 电动汽车接入下的电网多目标交易

在多目标交易中，购电费和排放量均希望越小越好，但当购电费用越小时，其排放量越大。反之亦然，是矛盾的两个方面。用多目标可以兼顾双方，使得经济效益和环保效益折中得到最优解。在已获得电动汽车功率的基础上，进一步构建多目标函数，将购电费用和排放量转化为隶属度函数 （单目标），使用内点法进行最优解的计算。

3.1 多目标优化交易模型

3.1.1 购电费用最小

购电费用最小的目标函数为

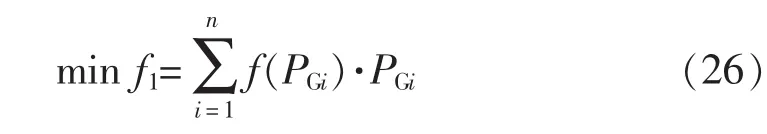
式中：f （PGi）=αpiPGi+bpi为有功报价曲线；PGi为 i机组有功出力，且为一次上升型。以上函数均化为标幺值计算。

3.1.2 污染气体的排放量最小

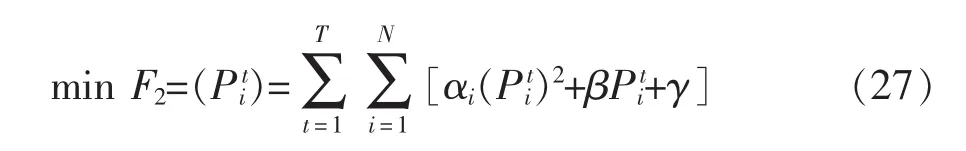
式中：α、β 、γ 为机组 i的污染排放系数，N=4，T=24。

以购电费用和污染物排放量最小为目标，以发电单元的发电量作为模糊变量，将多目标进行模糊化。选择最大满意度法作为隶属度函数对多目标函数进行模糊化建模。对于这一类没有下限但有上限的多目标优化问题，采用隶属度函数为降半直线型［7］，两个多目标优化隶属度函数可分别用式（28）、式（29）表示，相应图示参见图5、图6。

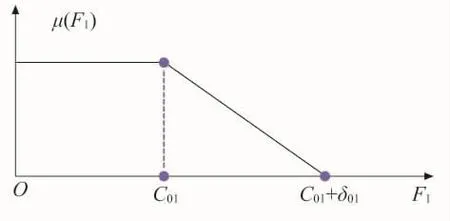
图5 购电费用最小隶属度函数曲线

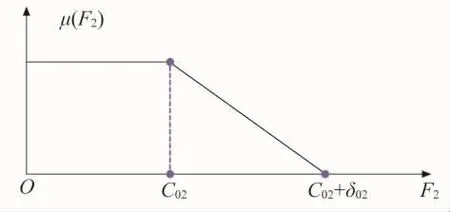
图6 污染气体排放量最小隶属函数曲线

3.1.3 机组约束条件

系统功率平衡约束为：

系统功率备用约束为：

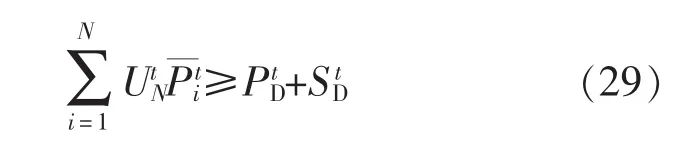
机组输出功率约束为：

隶属函数为

图 5 中，c01＋δ01表示购电费用最大可接受值，δ01为期望的最大费用节约，c01≤δ01≤c′01中，c01表示以购电费用最小为目标函数优化时对应的购电费用值，c′01表示以污染气体排放量最小为目标函数优化时对应的购电费用，取δ01＝（c01＋c′01） ／2；图 6 中c02＋δ02表示污染气体排放量最大可接受值，δ02为期望的排放量的最大节约值，c02≤δ02≤c′02。 c02、c′02分别表示以购电费用最小和以污染气体总排放量最小为单目标优化的数值。将以上参数计算出来带入式（28）、式（29），在此基础上对各个目标函数进行缩放，从而可以进行下一步的优化工作。

通过以上方法处理可以将多目标优化调度问题转化为单目标问题：

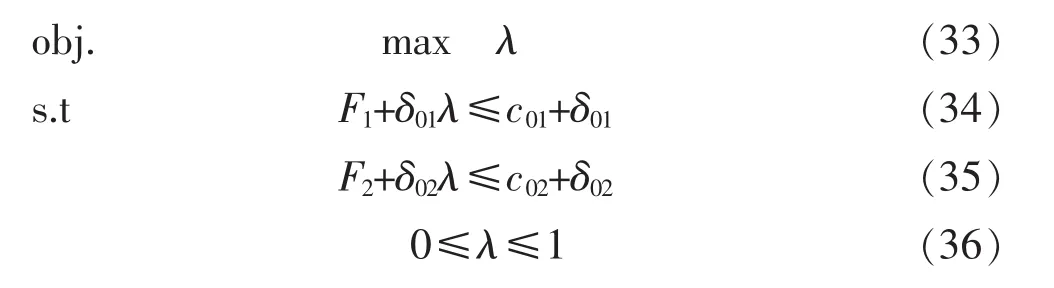
式中：λ＝min（μ（F1），μ（F2））。

3.2 算例仿真和结果分析

通过Matlab仿真可得多目标最优解数据如表8所示。

3.3 数据分析

以上数据与单目标数据比较后可得：1）采用多目标模糊优化后，购电成本比其作为单目标时高0.02%；2）排量比其作为单目标时高约0.018%；3）多目标优化数据是折中的最优解，此解与相应的单目标最优解的接近程度取决于隶属函数λ的大小，λ最接近于1时多目标取得最优解。

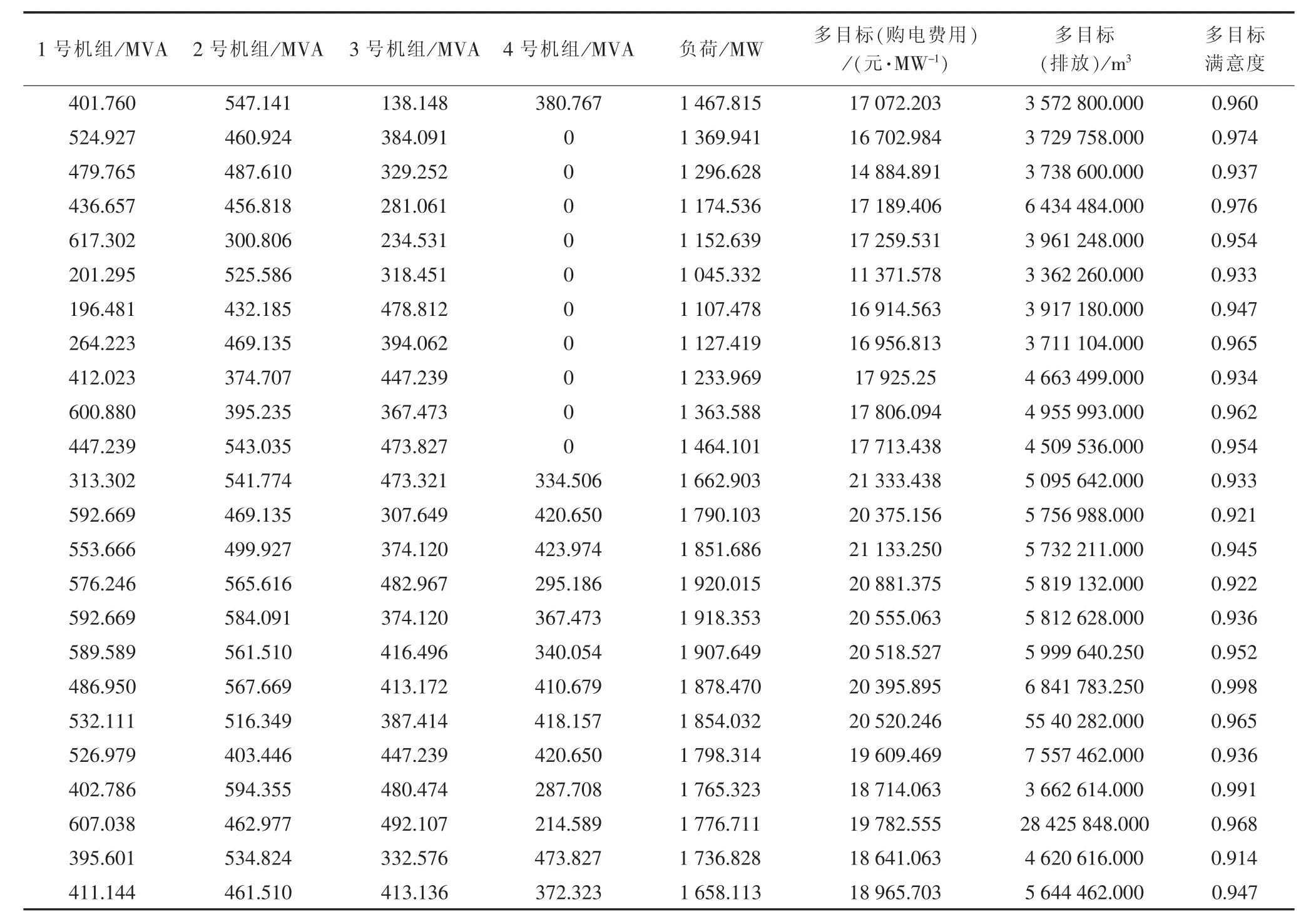
表8 多目标最优解

因此多目标函数可以求得购电费用最小和排放量最小的最优解，即通过多目标可以实现电网经济效益和环保效益的最大化，该结论值得我们进一步研究和探索。

4 结语

在电动汽车功率的预测及计算中，考虑了电动汽车实际的充放电情况，并根据电动汽车的V2G特性，利用粒子群优化算法来进行负荷计算。在接入电网后，分别求以购电费用和排量为单目标的函数，确定其约束条件，进行仿真分析。进一步，利用各最优解将子目标函数模糊化（即确定隶属函数），求使交集的隶属度函数取最大值的解，得到多目标优化问题的最优解。通过算例仿真可以看出，电网的多目标交易具有良好的经济效益和环保效益。

［1］吴春阳，黎灿兵，杜力，等．电动汽车充电设施规划方法［J］.电力系统自动化，2010，34（24）：36-39，45.

［2］田立亭，史双龙，贾卓．电动汽车充电功率需求的统计学建模方法［J］.电网技术，2010，34（11）：126-130.

［3］韩中庚．实用运筹学：模型、方法与计算［M］.北京：清华大学出版社，2007.

［4］梅振宇，陈峻，王炜.城市路内停车设置规模非线性优化模型及其算法［J］.交通运输工程学报，2007，7（2）：89-93.

［5］U.NARAYAN.Bhat.An Introduction to Queueing Theory：Modeling and Analysis in Applications［J］.Birkhuser Boston，2015，59（2）：14.

［6］GARCIA－VALLE R and VLACHOGIANNIS J.G.Electric vehicle demand model for load flow studies［J］.Electric Power Components&Systems，2009，37（5）：577－582.

［7］SABER A Y，VENAYAGAMOORTHY G K.Intelligent unit commitment with vehicle-to-grid：a cost-emission optimization［J］．Journal of Power Sources，2010，195（3）：898-911.

Multi-Objective Optimization Transaction Research of the Grid Under the Electric Vehicles Access Abstract

ZHANG Wen，LI Kai，WANG Nan，YU Qianqian，DENG Shaozhi
（State Grid Shandong Electric Power Company Economic Research Institute，Jinan 250021，China）

TM71

A

1007－9904（2017）09－0006－08

2017-07-11

张 雯（1989），女，从事配电网规划工作；李 凯（1988），男，中级工程师，从事配电网规划工作；王 男（1989），女，中级工程师，从事输电网规划工作；于千千（1987），女，中级工程师，从事建设管理技术经济审查工作；邓少治（1990），男，从事配电网规划工作。