基于五阶球面单纯形-径向容积准则的多终端一致分布式滤波定轨算法

2017-10-14李兆铭杨文革

电子与信息学报 2017年3期

李兆铭杨文革丁丹王超

李兆铭*①杨文革②丁丹②王超③

①(装备学院研究生院北京 101416)②(装备学院光电装备系北京 101416)③(西安卫星测控中心西安 710043)

为了提高多手持终端信息融合实时定轨的精度和系统容错性，该文提出一种基于五阶球面单纯形-径向容积准则的多终端一致分布式容积信息滤波(CD-SSRCIF)定轨算法。分别使用维单纯形顶点和矩匹配法计算球面和径向积分，得到适用于系统状态维数7时的五阶球面单纯形-径向容积准则。利用统计线性误差传播方法将此五阶容积准则嵌入扩展信息滤波器，将集中式变量展开得到多源集中式五阶容积信息滤波器。进而，利用平均一致性算法对集中式滤波中多源信息累加进行分布式等价表示，构成上下两层级联滤波器，下层滤波器执行平均一致性算法融合邻居节点的信息，输出虚拟量测值。上层滤波器利用该量测值执行五阶容积信息滤波，实时输出轨道状态估计值。仿真实验结果表明，五阶CD-SSRCIF算法无需信息融合中心，且具有比三阶算法更高的定轨精度。

手持终端；五阶球面单纯形-径向准则；分布式滤波；实时定轨

1 引言

地基空间目标监视目前主要是利用雷达对空间目标进行实时定轨来实现[1]。区别于雷达设备复杂且机动性弱的特点，手持终端(下文简称终端)更便于携带且易于操作。终端上安装有小型全向杆状天线，采用多普勒原理[2]测量其与卫星之间的径向距离变化率，即仅具有测速元素，设备简单且误差源少。以某颗在轨运行的小卫星为例，其S频段下行遥测频率为2.3 GHz, EIRP值为3 dBW，当终端天线增益设计为0 dB时，终端的有效作用距离约为1100 km，即对轨道高度400 km以下的卫星在最低仰角的过境弧段内可以保证0.1 m/s的测速误差。因此使用终端对低轨卫星进行应急测控便成为对传统雷达测控的一种有效补充。

多终端利用测速值对轨道状态进行实时确定属于最优状态估计问题。作为信息融合研究的热点，分布式估计无需融合中心，每个节点仅与其邻居节点进行信息交互，通过每个节点局部信息在网络中的流动得到与集中式估计一致的精度，在提高系统容错性的同时降低了通信能量消耗[3]。其中，Olfati针对线性系统提出了分布式卡尔曼滤波(Distributed Kalman Filter, DKF)算法，该算法可以有效克服网络中各节点局部估计的差异，使得所有节点估计趋于一致。对于非线性系统，使用扩展卡尔曼滤波[7]对DKF算法进行拓展可以得到分布式扩展卡尔曼滤波[8](Distributed Extended Kalman Filter, DEKF)算法。但DEKF对非线性函数的一阶泰勒截断使得其仅具有一阶滤波精度。文献[9]将无迹变换[10]直接嵌入DEKF算法的更新方程，采用Sigma点对概率密度函数进行近似，提高了对非线性系统的滤波精度。文献[11, 12]提出了由无迹信息滤波器和平均一致性滤波器级联构成的分布式无迹信息滤波(Distributed Unscented Information Filter, DUIF)算法。但上述研究均是基于无迹变换展开，该变换更适用于系统状态维数不大于3时的情况。Arasaratnam等人[13]基于三阶球面-径向容积准则提出了容积卡尔曼滤波(Cubature Kalman Filter, CKF)算法，避免了UKF参数选取的盲目性，对于高阶系统具有更高的精度和稳定性，已在许多领域取得了应用[14,15]。文献[16]基于信息滤波和平均一致性算法提出分布式CKF滤波算法，具有比DUIF更高的滤波精度和稳定性。但上述CKF算法在采样点的构造中均是采用三阶球面-径向容积准则，限制了精度的进一步提高。

本文提出一种基于五阶球面单纯形-径向容积准则的多终端一致分布式容积信息滤波(Consensus-based Distributed Spherical Simplex Radial Cubature Information Filter, CD-SSRCIF)定轨算法，该算法具有五阶滤波精度的同时，适用于系统状态维数7的情况，仿真实验结果验证了本文算法的有效性。

2 五阶球面单纯形-径向容积准则

非线性系统贝叶斯滤波的核心是计算高斯加权积分，文献[13]将向量函数积分分解为球面积分和径向积分，并给出了三阶球面-径向准则的详细推导过程。本文采用维单纯形计算球面积分，构造如式(1)五阶球面单纯形准则：

(2)

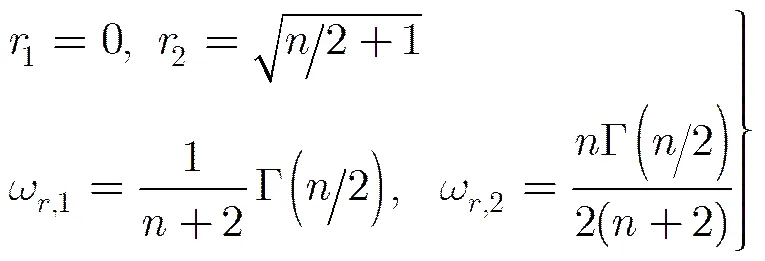
(4)

3 五阶球面单纯形-径向一致分布式容积信息滤波算法

考虑如式(5)离散非线性动态系统：

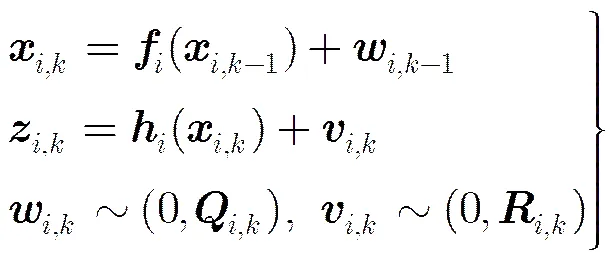
3.1 五阶集中式容积信息滤波器

(7)

将式(4)所示五阶球面单纯形-径向准则嵌入EIF的更新方程，并代入式(7)，式(8)，便可得到五阶集中式SSRCIF算法。当有多源量测信息时，按照集中式滤波定义变量和矩阵：,,,，则可以推导出集中式滤波的信息矩阵贡献，信息状态贡献。

3.2 五阶一致分布式容积信息滤波器

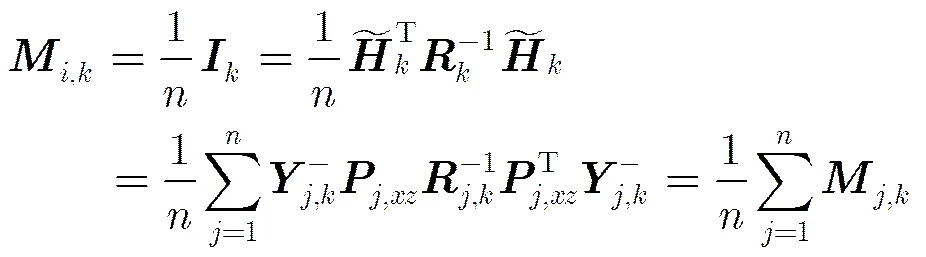
(11)

则状态更新方程可以写为

(13)

步骤1 初始化：

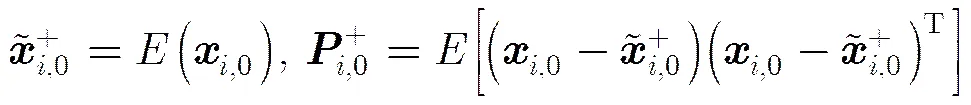
步骤2 时间更新：

(15)

(17)

(18)

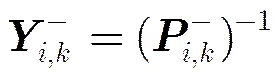
(20)

步骤3 量测更新：

(22)

(23)

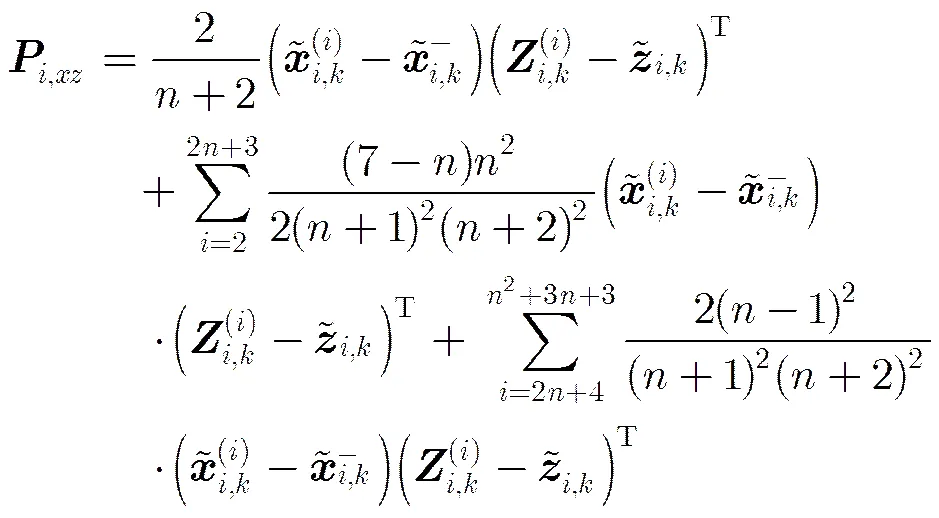
(25)

设定初始值：

(27)

(29)

步骤4 状态更新：

(31)

(32)

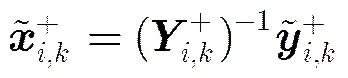
4 仿真实验

以带2项引力摄动的卫星轨道动力学方程为状态方程，以地平坐标系中终端测速方程为量测方程，具体参见文献[21]，基于MATLAB软件平台对本文提出的定轨算法进行验证。参考轨道数据由STK中HPOP算法产生，该算法考虑了大气阻力、太阳光压和三体引力等摄动影响，是可靠的轨道仿真数据来源。考虑小偏心率椭圆轨道卫星，其历元为1 Jul 2015 03:00:10(UTCG)，轨道6根数分别为：km,,,,,, 6个终端经纬度分别为(107.993°, 25.766°), (117.27°，27.512°), (111.179°, 25.968°), (115.089°, 25.048°), (111.213°, 23.583°), (114.541°, 27.839°)。星上S频段下行遥测频率为2.3 GHz, EIRP值为3 dBW，信息速率为1024 bit/s。终端采用全向杆状天线，天线增益为0 dB，信号采用BPSK调制方式。为了能够正确解调，在误码率为时，解调门限为10.6 dB。同时，为了保证0.1 m/s的测速精度，要求载噪比。考虑链路余量为4 dB，由链路预算结果可以得到，(E/0)min=11.009>10.6 dB, (/0)min=41.112>40，满足指标，从而验证了终端测速的可行性。

滤波定轨初值一般由地面测控中心测量提供，并外推至滤波起始时刻，仿真中取为

初始协方差矩阵为

状态噪声方差矩阵为

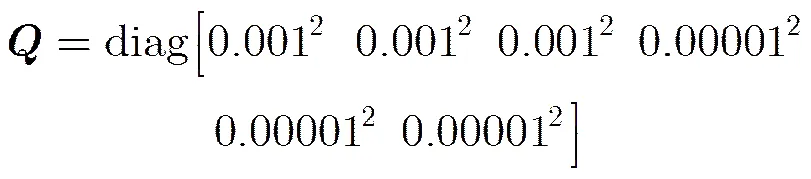
考虑6个终端间的通信拓扑结构如图1所示。

本文提出的算法不仅适用于终端定轨，同样适用于传统地基雷达定轨，相比于终端仅具有测速功能，雷达的测量元素为测距、测速和测角。假设雷达测距精度为20 m，测速精度为0.1 m/s，测角精度为0.015°, 6个雷达间的通信拓扑关系如图1所示。仿真中考虑3种情况，分别为在终端上运行三阶CD-SSRCIF算法、在终端上运行本文提出的五阶CD-SSRCIF算法和在雷达上运行五阶CD-SSRCIF算法。取滤波周期=1.0 s，运行200次蒙特卡洛仿真，以终端(雷达)1为例，给出3种情况的结果对比如图2所示。统计100~160 s内3种情况的平均定位RMSE和平均定速RMSE，并列于表1。从图2中可以看出，多终端间通过信息一致性交互可以实现定轨计算的快速收敛。对比在终端上运行的两种算法，本文提出的五阶CD-SSRCIF算法具有比三阶CD-SSRCIF算法更高的定轨精度，在本文仿真条件下，将定位精度提高了2 m，定速精度提高了0.025 m/s。对比五阶CD-SSRCIF算法分别在终端上和雷达上运行的情况，在本文仿真条件下，雷达定位精度比终端高7.5 m，定速精度比终端高0.02 m/s，而且由于雷达的测量元素更多，因此滤波收敛速度更快。虽然雷达的定轨精度更高，但终端的部署与应用更为灵活，而且终端对低轨卫星10.9 m的定位精度已经可以满足低轨卫星的应用需求。

图1 6个终端间通信拓扑结构图

5 结论

为了提高多手持终端实时定轨的精度和系统容错性，本文提出一种多终端五阶CD-SSRCIF定轨算法。该算法由两层滤波器级联而成，下层滤波器执行一致性算法融合邻居发送的信息，输出虚拟量测值。上层滤波器利用该量测值执行五阶容积信息滤波，实时输出定轨值。仿真实验结果表明：(1)多终端通过一致性信息交互可以实现滤波计算的快速收敛，且本文提出的五阶CD-SSRCIF算法具有比三阶算法更高的定轨精度。在本文仿真条件下，将定位精度提高了2 m，定速精度提高了0.025 m/s；(2)将五阶CD-SSRCIF算法应用于多雷达定轨可以得到更高的定轨精度，在本文仿真条件下，雷达定位精度比终端高7.5 m，定速精度比终端高0.02 m/s，但终端的部署与应用更为灵活，而且终端对低轨卫星10.9 m的定位精度已经可以满足低轨卫星的应用需求。

图2 3种情况定轨RMSE对比

表1 100~160 s 3种情况定轨平均RMSE

[1] 李志军, 侯黎强. 一种用于实时轨道确定的NPF-SRCKF滤波算法[J]. 宇航学报, 2014, 35(7): 812-816.

LI Zhijun and HOU Liqiang. An improved NPF-SRCKF based algorithm for spacecraft orbit determination[J]., 2014, 35(7): 812-816.

[2] 潘文, 蒋占军, 杜正锋, 等. 分布式移动通信系统中基于多普勒测速与卡尔曼滤波的动态定位算法[J]. 电子与信息学报, 2008, 30(6): 1421-1423.

PAN Wen, JIANG Zhanjun, DU Zhengfeng,. An algorithm for dynamic location based on Doppler velocity estimation and kalman filtering in distributed mobile communication system[J].&, 2008, 30(6): 1421-1423.

[3] 杨文, 侍洪波, 汪小帆. 卡尔曼一致滤波算法综述[J]. 控制与决策, 2011, 26(4): 482-486.

YANG Wen, SHI Hongbo, and WANG Xiaofan. A survey of consensus based Kalman filtering algorithm[J]., 2011, 26(4): 482-486.

[4] OLFATI S R. Distributed Kalman filter with embedded consensus filters[C]. The 44th IEEE Conference on Decision and Control, and the European Control Conference, Seville, Spain, 2005: 8179-8183.

[5] OLFATI S R. Distributed Kalman filtering for sensor networks[C]. Proceedings of the 46thIEEE Conference on Decision and Control, New Orleans, USA, 2007: 5492-5496.

[6] OLFATI S R. Kalman-Consensus filter: optimality, stability, and performance[C]. The 48th IEEE Conference on Decision and Control, Shanghai, China, 2009: 7036-7041.

[7] BOLOGNANI S, TUBIANA L, and ZIGLIOTTO M. Extended kalman filter tuning in sensorless PMSM drives[J]., 2003, 39(6): 1741-1747.

[8] GIROGIO B and LUIGI C. Stability of consensus extended Kalman filtering for distributed state estimation[C]. Preprints of the 19th World Congress the International Federation of Automatic Control, Cape Town, South Africa, 2014: 5520-5525.

[9] 杨小军. 基于Unscented信息滤波器的分布式目标融合跟踪[J]. 吉林大学学报(工学版), 2015, 45(2): 659-661. doi: 10.13229/j.cnki.jdxbgxb201502048.

YANG Xiaojun. Distributed fusion and target tracking based on unscented information filter[J].(), 2015, 45(2): 659-661. doi: 10.13229/j.cnki.jdxbgxb201502048.

[10] JULIER S J, UHLMANN J K, and DURRANT. A new method for nonlinear transformation of means and covariances in filters and estimators[J]., 2000, 45(3): 477-482.

这个说法是错误的。判断一颗牙齿有没有蛀牙或者龋坏，是要从色、形、质这三个方面来判断的。比如说颜色会发生变化，不一定是发黑，有时候可以呈棕色、褐色、黄色都有可能，甚至白褐色；质地会发软，正常的牙齿是非常坚硬的，但是质地变化以后，用尖锐的探针，就能刮下来；外形也会发生变化，可能形成一些孔洞，能发现并探进去。

[11] LI W L and JIA Y M. Consensus-based distributed multiple model ukf for jump markov nonlinear systems[J]., 2012, 57(1): 230-236. doi: 10.1109/TAC.2011.2161838.

[12] 汤文俊, 张国良, 曾静, 等. 一种适用于稀疏无线传感器网络的改进分布式UIF算法[J]. 自动化学报, 2014, 40(11): 2491-2496. doi: 10.3724/SP.J.1004.2014.02490.

TANG Wenjun, ZHANG Guoliang, ZENG Jing,. An improved distributed unscented information filter algorithm for sparse wireless sensor networks[J]., 2014, 40(11): 2491-2496. doi: 10.3724/SP.J.1004.2014.02490.

[13] ARASARATNAM I and HAYKIN S. Cubature Kalman filters[J]., 2009, 54(6): 1254-1269. doi: 10.1109/TAC.2009.2019800.

[14] 宁夏, 叶春茂, 杨健, 等.容积卡尔曼滤波在空间目标轨道确定中的应用[J]. 电波科学学报, 2014, 29(1): 27-32. doi: 10.13443/j.cjors.2013030101.

NING Xia, YE Chunmao, YANG Jian,. Cubature Kalman filtering for orbit determination of space targets[J]., 2014, 29(1): 27-32. doi: 10.13443/j.cjors.2013030101.

SHAN Ganlin, ZHANG Kai, and JI Bing. Pose angle aided target tracking algorithm based on Gaussian sum square-root cubature Kalman filter[J].&, 2014, 36(7): 1580-1583. doi: 10.3724/ SP.J.1146.2013.01474.

[16] 丁家琳, 肖建, 张勇. 基于CKF的分布式滤波算法及其在目标跟踪中的应用[J]. 控制与决策, 2015, 30(2): 297-302. doi: 10.13195/j.kzyjc.2013.1356.

DING Jialin, XIAO Jian, and ZHANG Yong. Distributed algorithm-based CKF and its applications to target tracking[J]., 2015, 30(2): 297-302. doi: 10.13195/j.kzyjc.2013.1356.

[17] 朱奇光, 袁梅, 王梓巍, 等. 机器人球面单径容积FastSLAM算法[J]. 机器人, 2015, 37(6): 709-716. doi: 10.13973/j.cnki. robot.2015.0708.

ZHU Qiguang, YUAN Mei, WANG Ziwei,. A robot spherical simplex-radial cubature FastSlam algorithm[J]., 2015, 37(6): 709-716. doi: 10.13973/j.cnki.robot. 2015.0708.

[18] ZHOU Zhenwei, FANG Haitao, and HONG Yiguang. Distributed estimation for moving target based on state-consensus strategy[J]., 2013, 58(8): 2097-2100. doi: 10.1109/TAC.2013. 2246476.

[19] ZHU Minghui and SONIA M. Discrete-time dynamic average consensus[J]., 2010, 46: 322-329. doi: 10.1016/j. automatica.2009.10.021.

[20] LI W and JIA Y. Consensus-based distributed information filter for a class of jump Markov system[J]., 2011, 5(10): 1214-1222. doi: 10.1049/ iet-cta.2010.0240.

[21] 李兆铭, 杨文革, 丁丹, 等. 基于SVD的多终端实时定轨自适应鲁棒CKF算法[J]. 仪器仪表学报, 2016, 37(3): 491-496.

LI Zhaoming, YANG Wenge, DING Dan,. Adaptive robust CKF algorithm for real time orbit determination of multiple hand-held terminals based on SVD[J]., 2016, 37(3): 491-496.

Five Order Consensus-based Distributed Spherical Simplex Radial Cubature Information Filter for Orbit Determination by Multiple Handheld Terminals

LI Zhaoming①YANG Wenge②DING Dan②WANG Chao③

①(,,101416,)②(,,101416,)③(’,’710043,)

A Consensus-based Distributed Spherical Simplex Radial Cubature Information Filter (CD-SSRCIF) is proposed to improve the real time orbit determination accuracy and fault tolerance of multiple handheld terminals. N-simplex vertices and the moment matching method are used respectively to calculate the spherical and radial integral, and a five order spherical simplex radial rule suitable for system state dimension7 is obtained. Statistical linear error propagation method is used to embed the above rule into Extended Information Filter (EIF) to achieve centralized five order cubature information filter. Then, average consistency algorithm is used to obtain the distributed equivalent expression of multi-source information accumulation in centralized filter, and constitute cascade filter. The lower filter performs an average consistency algorithm to fuse information from neighbor nodes, and output virtual measurement value. The upper filter performs five order cubature information filter with the above measurement value to output orbit state estimation in real time. The simulation results show that the five order CD-SSRCIF algorithm does not need information fusion center, and has a higher orbit determination accuracy than the three order algorithm.

Handheld terminal; Five order spherical simplex radial rule;Distributed filter; Real time orbit determination

V249.3

1009-5896(2017)03-0703-06

10.11999/JEIT160431

2016-04-29；改回日期：2016-09-14；

2016-11-14

李兆铭 lizhaomingzbxy@163.com

国家高技术研究发展计划(2015AA7026085)

The National High Technology Research and Development Program of China (2015AA7026085)

李兆铭：男，1989年生，博士生，研究方向为航天测控最优估计方法.

杨文革：男，1966年生，教授，博士生导师，主要研究方向为现代信号处理.