含锂电池储能的船舶电力系统模型预测控制研究
2017-10-14何志祥肖健梅王锡淮
何志祥,肖健梅,王锡淮
含锂电池储能的船舶电力系统模型预测控制研究
何志祥,肖健梅,王锡淮
(上海海事大学,上海201306)
由于船舶运行的特殊性和负载波动的复杂性,严重影响船舶电力系统的稳定性,因此引入了能量存储技术,降低电网的波动。根据发电机和锂电池的状态空间模型,建立了含锂电池储能的船舶电力系统,并提出了一种基于模型预测控制的船舶电力系统。在含有负载波动的情况下,使发电机和锂电池的输出能够稳定跟随负载的变化,从而满足负载的需求。并将整个系统在Matlab/Simulink中进行实例仿真,仿真结果表明,在模型预测控制下的船舶电力系统能够很好地满足负载波动需求,明显改善船舶电力系统的稳态性能,增强船舶电网的稳定性。
船舶电力系统 储能技术 发电机 锂电池 模型预测控制
0 引言
船舶电力系统是船舶管理系统的重要组成部分,是目前大部分船舶保障航行稳定推进,船舶稳定供电的基础。随着船舶技术的发展和综合电力系统的应用的深入,国内外都在积极从事适用于综合电力系统的智能化能量管理系统的研究。总体来说,国内在船舶电力系统上的研究起步较晚[1-3]。而传统的只靠柴油发电机发电的船舶电力系统的电能质量和利用及其的稳定性、安全性方面存在很大的局限性。
随着能量存储技术的发展和应用,上述问题得到了很好的解决[4]。目前,主流的能量存储方式有:超导储能,超级电容器储能,飞轮储能,蓄锂电池储能等。其中,锂电池因其经济性,高性能,在各种电力系统中被广泛应用。在船舶电力系统中使用锂电池的目的主要有以下几点:
1) 提供短时供电。当在船舶电力系统中突加大功率负载时,柴油发电机所产生的电能不足以负荷负载工作时,锂电池可以提供短时的供电,以达到船舶电力系统母线中电压,电流的稳定。
2) 充分利用电能。当柴油发电机产生的电能高于船舶负载所需时,锂电池可以吸收多余的电能,以达到充分利用的效果。
3) 提高电能质量和电力系统的安全性。船舶电力系统中,非线性负载较多,影响电力系统稳定性的不利因素较多,锂电池的加入可以稳定母线电压,保持电力系统的稳定运行,提高船舶的电能质量。
本文首先建立了船舶电力系统中发电机和锂电池模块的数学模型,并对系统进行了模型预测控制仿真。对有锂电池储能的船舶电力系统的稳定性和可行性进行了分析研究。
1 船舶电力系统的控制原理和模型建立
1.1 船舶电力系统的控制原理分析
为了使船舶电力系统具有更好的稳定性,引入锂电池,我们采用的控制原理具体如图1。
首先将发电机所需要产生的功率和锂电池所需要吸收或者释放的功率输入给模型预测控制器,由模型预测控制器输出各个模块的输入,并将所得输入进一步给发电机和锂电池模块,从而达到控制的目的,使发电机和锂电池能够稳定跟随其各种功率的变化。
1.2模型的建立
1.2.1发电机模型
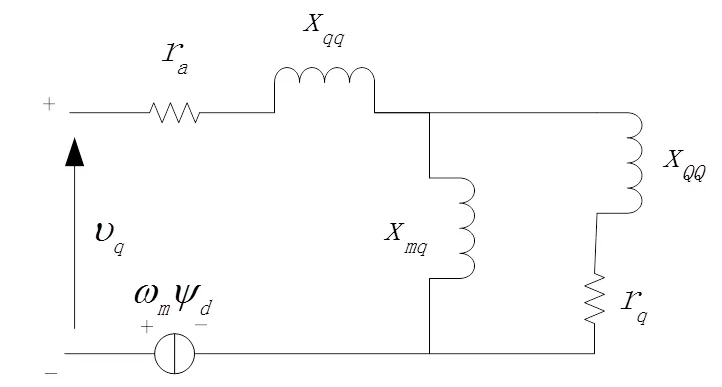
在同步电机dq0坐标系Park方程的基础上,引入两个补偿电抗补偿磁滞饱和引起的非线性特性,得到改进的dq轴等效电路图如图2所示[6-7]。根据图2所示(图中,v为励磁电压,i、i分别为d、q轴电流,i为励磁电流,v、v为d、q轴电压;为电机的转速,=1)。,由文献5、文献6和文献7,我们可以得到发电机的三阶电磁方程如下:
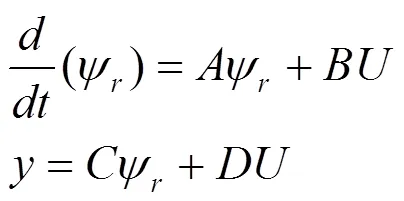
其中
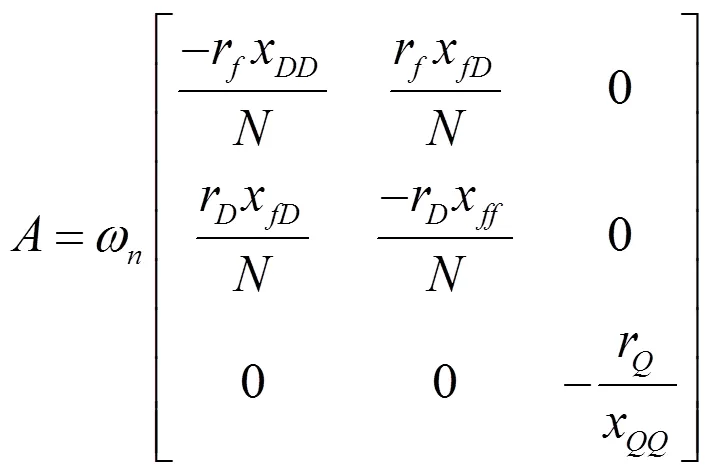
(3)
(4)
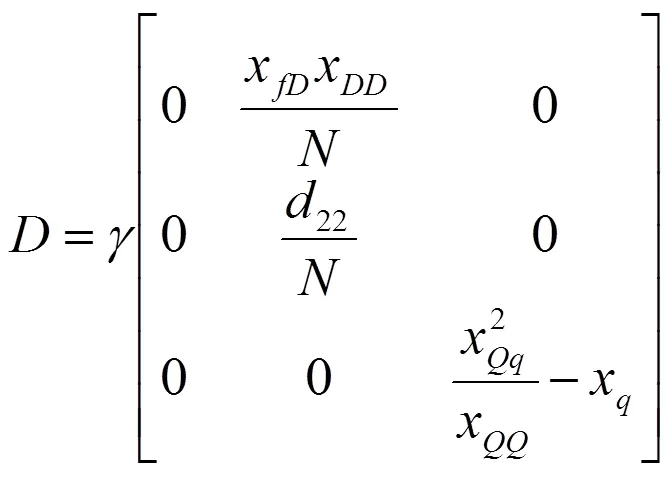
1.2.2锂电池模型
锂电池的仿真模型采用以电池的实际容量Q和电池过滤后的电流I做为状态变量的数学模型,该锂电池模型由可控的电压源和恒值电阻串联组成。其充电的数学模型如下[8-10]:

(a)
(b)
其放电模型将公式改为如下公式即可:
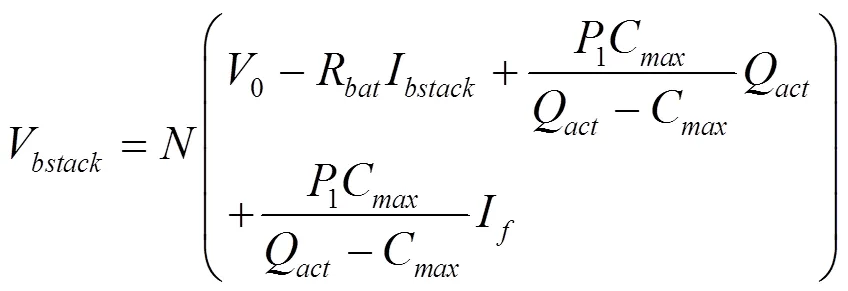
其中,V,I,SOC分别是电池组的电压,电流和荷电状态。I是在时间T下的电池过滤电流,Q为电池的实际电量,C为电池的最大电量,R为电池内阻,为电池初始电压,1为与电池有关的常系数。公式(9)~(11)描述了电池通过DC/DC转换器与母线相连后,电池的电压,电流与直流母线上的电压,电流的关系。
2 模型预测控制
模型预测控制是一种基于模型的闭环优化控制策略[11]。其控制原理如图3所示。
模型预测的三要素是预测模型,滚动优化,反馈校正。其算法的核心是使用系统模型来预测状态变量在预定义时间段内的未来行为,从中选择一个使价值函数最小化的状态变量,作用于下一个周期。

图3 模型预测控制原理图
一般地,模型预测算法有模型算法控制(MAC),动态矩阵控制(DMC),广义预测控制(GPC)和状态反馈预测控制。
根据我们建立的状态空间模型,最合适的应该是状态反馈预测控制,但由于其原理上忽略了D矩阵对系统的影响,因此我们不采用状态反馈预测控制。而欲使用广义预测控制,就我们建立的模型来看,牵涉到模型的解耦,这无形中增加了算法的难度。因此我们选择动态矩阵控制或者模型算法控制。下面我们简单介绍一下动态矩阵控制。
2.1预测模型
动态矩阵控制直接以受控系统的阶跃响应离散系统为模型。当有M个控制增量时,系统在未来P时刻的预测输出为:
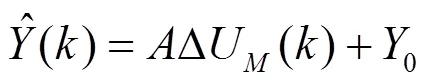
矩阵A为P*M维的常数阵,它完成由系统的阶跃响应参数所决定,反映了系统的动态特性,因此又称为动态矩阵。P为预测时域,M为控制时域。
2.2滚动优化
系统的模型预测是根据动态响应参数和控制增量决定的,而控制增量是通过使优化指标J最小来确定的。以使未来P个输出预测值尽可能地接近期望值。一般地,滚动优化采用二次型性能指标作为目标函数,其表达式如下:
其中,
2.3反馈校正


因此,利用这一误差对未来时刻其他预测值进行校正。则有
(16)
3 系统的仿真和分析
将电池状态方程看成是以I为状态变量的方程。结合发电机的三阶状态方程,可以将发电机和电池结合扩展成一个四阶的状态方程如下:


某发电机参数[5]如表1所示。
本文所用的电池为加拿大CORVUS公司生产的AT6700-100电池,其详细参数见表2.
以某艘破冰船的某种工况为例,在运行一个发电机和锂电池的过程中,其各自的功率波动如图4所示。
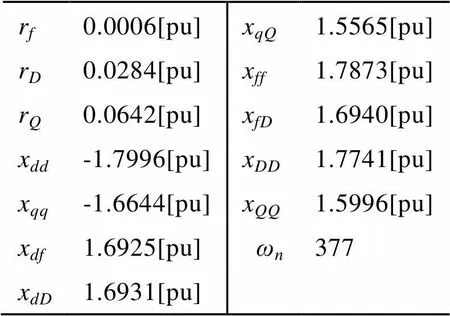
表1 同步发电机主要参数
表2 AT6700-100电池参数

将方程(17)的阶跃响应模型作为预测模型,采用二次型性能指标作为目标函数,对控制器进行反馈校正,设计模型预测控制器,并根据图1的控制策略进行Matlab/Simulink仿真,MPC控制器参数设置如下:

图4 发电机和锂电池功率波动图
图5显示了经过模型预测控制后得到的实际控制输入。图6是参考输出与实际输出的对比,图中实线为参考曲线,虚线为实际曲线,开始阶段,给出的参考曲线是系统稳定后的参考曲线,而实际曲线仿真时应该从0开始,有一个上升的过程,因此此时的差距较大。其他时刻,可用看出除了功率突变比较大时,跟踪效果稍差外,其他时候发电机都有一个比较好的跟踪效果;而电池的跟踪情况较好。图7为电池的电压及SOC变化,可以看出单个电池的仿真结果在合理范围内。
结合发电机和锂电池功率变化分析,引入模型预测控制后,发电机和锂电池可以较好的跟踪其各自的功率变化,提高了系统的稳定性,增加了船舶电力系统的寿命。

图5 MPC得到的实际控制输入图

图6 预测输出与实际输出对比图

图7 电池电压变化及SOC变化
4 总结
针对船舶电力系统,通过建立系统的状态方程,引入模型预测控制,设计了含有锂电池储能的船舶电力系统。通过对系统的仿真,证实了引入模型预测控制以后,发电机和锂电池可以较好地跟踪功率的波动,改善了船舶电力系统的稳定性。
[1] 冒如权. 舰船能量管理系统现状及发展趋势[J]. 上海船舶运输科学研究所学报, 2012(1): 19-22
[2] 宋波. 船舶能量管理系统设计研究[J]. 中国舰船研究, 2011(2): 93-97
[3] 韩旗, 黄一民, 张纪元等. 船舶能量管理系统技术[J]. 船舶工程, 2009(31): 102-104
[4] K. Bellache, M. B. Camara, Z. Zhou, B. Dakyo. Energy management in hybrid electric boat based on frequency distribution approach using diesel, lithium-battery and supercapacitors. Vehicle Power and Propulsion Conference (VPPC), 2015, 19-22.
[5] Tommy Andy Theubou Tameghe. Modélisation et Simulation d'un Système de Jumelage éolien-diesel Alimentant Une Charge Locale, Université du québec. 2012, (8):85-90, 93-108
[6] RenÉ Wamkeue; Frederic Baetscher; Innocent Kamwa, “Hybrid-state-model-based time-domain identifica- tion of synchronous machine parameters from saturated load rejection test records”, IEEE Journals & Magazines, 2008, (23): 68-77.
[7] 刘勇智, 刘聪. 基于状态空间法的航空同步发电机建模方法研究[J]. 微电机, 2011,(44): 48-51.
[8] Olivier Tremblay1, Louis-A. Dessaint. Experimental validation of a battery dynamic model for EV applications. World Electric Vehicle Journal. Vol. 3 – ISSN 2032-6653-© 2009 AVERE, EVS24 Stavangern, Norway, 2009, (10): 13-16,.
[9] Arash M. Dizqah, Alireza Maheri, Krishna Busawon, and Azadeh Kamjoo. A multivariable optimal energy management strategy for standalone DC microgrids”, IEEE Transactions on Power Systems, 2015, 30(5): 2278 – 2287.
[10] Arash M. Dizqah, Alireza Maheri, Krishna Busawon, Peter Fritzson. Acausal modelling and dynamic simulation of the standalone wind-solar plant using modelica, Computer Modelling and Simulation (UKSim), 2013 UKSim 15th International Conference on: 580–585.
[11] 叶列杰甫, 滕青芳. 基于预测控制的光伏阵列最大功率点跟踪方法[J]. 兰州交通大学学报, 2017(1): 77-83.
Research on Model Predictive Control of Ship Power System with Lithium Battery Energy Storage
He Zhixiang, Xiao Jianmei, Wang Xihuai
(Shanghai Maritime University, Shanghai 201306, China)
N945.12
A
1003-4862(2017)08-0043-0006
2017-04-14
何志祥(1993- ),男,硕士研究生,研究方向为复杂系统控制与优化。Email: hezhixiang_hzx@163.com
肖健梅(1962-),女,教授。研究方向:智能控制、粗糙集理论、物流系统优化。
王锡淮(1961- ),男,教授,博士生导师。研究方向:预测控制,复杂系统建模与控制、系统优化。
