江西省不同立地等级的马尾松林生物量估计和不确定性度量*

赵 菡 雷渊才 符利勇

(中国林业科学研究院资源信息研究所 北京 100091)

江西省不同立地等级的马尾松林生物量估计和不确定性度量*

赵 菡 雷渊才 符利勇

(中国林业科学研究院资源信息研究所 北京 100091)

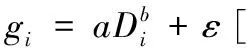
立地分级； 异速生长模型； 生物量估计； 不确定性估计； 蒙特卡洛模拟

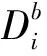
Keywords： site classification； allometric model； biomass estimates； uncertainty estimates； Monte Carlo simulation

立地生产力是森林抚育经营管理与制定决策方案的重要量化指标，对森林的可持续经营具有重要意义(Skovasgaardetal.， 2008；Berrilletal.， 2013)。森林生物量作为立地生产力的直接反映，与立地类型和质量息息相关(Satooetal.， 1982；Perietal.， 2010； Gargaglioneetal.， 2010)，且随着森林生物量估计在森林资源监测、森林碳汇评价、全球变化等方面的广泛应用，森林生物量估计研究已逐渐扩展至区域、国家乃至全球尺度，国内外在国家和区域尺度上已开展了大量森林生物量的测算和估计研究(Fangetal.， 2001；Peterssonetal.， 2012；李海奎等，2010)。大尺度(国家和区域)的森林生物量估计，通常采用通过系统方法布设样地的国家连续清查数据，建立单木胸径或树高和胸径与生物量之间的异速生长模型，估算样地生物量，并在此基础上推算区域尺度的生物量(McRobertsetal.， 2014)。由于立地条件的多样性或差异性，同一树种在不同区域的生物量估计结果以及由于存在不确定性导致的生物量估计误差也会随立地质量的不同而变化(Ketteringsetal.， 2001)，而忽略立地质量差异引起生物量估计结果以及生物量估计误差不同的结果必然是粗略且不精准的。此外，作为《联合国气候变化框架公约》的签署国，每个国家都有义务按照“三可原则”定期报告森林生物量和不确定性的估计结果。因此，研究精准估计不同立地条件下的森林生物量和生物量估计误差是大尺度生物量估计的重要方面。

以往研究中，在单木生物量模型中添加与立地质量有关的因子被认为是提高生物量模型估计精度的有效手段。如在建立单木生物量时，Ketterings等(2001)将与立地-树种相关的树高-胸径关系和立地平均木材密度作为变量加入到以胸径为自变量的生物量异速生长模型中，有效改进了生物量模型的估计精度； Li等(2013)利用树高分级法，用样地的林木平均树高划分等级代替立地因子，将林木等级以哑变量形式加入到以胸径为自变量的单木地上生物量及地上生物量各部分(干、枝、叶、皮)的异速生长模型中，估计精度和偏度，计算不同径级的树木生物量和偏差，获得了较好的估计效果。这些研究虽然提高了大尺度森林生物量的估计精度，但是不同立地条件或立地质量的生物量以及不确定性度量却未曾涉及。当以森林生产力作为森林经营目的时，立地质量的划分以及不同立地条件下的森林生物量和生物量误差估计是十分必要的(Skovasgaardetal.， 2008)。此外，估计不同立地等级的生物量，选择不同的异速生物量模型形式也会影响区域生物量的估计精度，这也是精准估计大尺度森林生物量及立地生产力的关键。

鉴于此，基于以下2个目的： 一是选择适合的单木生物量异速生长模型形式，二是在不同单木生物量模型基础上获得区域生物量及其不确定性在不同立地等级下的估计，本研究以江西省广泛分布且具有代表性的马尾松(Pinusmassoniana)林为研究对象，通过比较3种单木地上生物量模型对区域尺度不同立地条件下马尾松林地上生物量及误差估计的结果来获得较优的模型形式。采用树高分级法，用林木优势高等级代替立地质量分级，对立地质量进行评价。为获得不同立地条件下生物量的不确定性，采用蒙特卡洛模拟法，将生物量模型估计中的各种不确定性用误差来表示，并通过大量的重复模拟度量误差，探讨立地质量对采用单木生物量模型估计区域生物量不确定性的影响，以期为区域森林生物量的精确估计提供技术支持，为森林立地生产力的精确估计提供参考。

1 研究区概况与数据

1.1研究区概况

江西省(图1)地处我国东南偏中部长江中下游南岸，24°29′14″—30°04′41″N， 113°34′36″—118°28′58″E。气候温暖，雨量充沛，年均降水量1 341～1 940 mm，无霜期长，为亚热带湿润气候。马尾松作为该地区优势树种，广泛分布于东部、西部以及南部的山地。本研究以马尾松为对象研究其生物量及误差随立地质量的分布情况，对反映该地区的立地条件十分有代表性。

1.2数据收集与处理

研究数据来源于第六次国家森林资源连续清查数据。江西省样地为8 km×8 km的系统布设，全境范围内共有2 610块样地，样地面积0.066 7 hm2。选取马尾松林占优势的312块样地，共13 840株马尾松作为研究对象，样地分布见图1。对312块样地中所有马尾松样木胸径进行每木检尺(起测径阶5 cm)，作为估计该区域马尾松林地上生物量的调查数据(survey data，SD)。由于SD中没有实测的树高，因此在每块样地上选取3～5株胸径最大的样木并测量其树高作为该样地的优势木高(共967株)，以此作为用来建模划分立地等级的分级建模数据(site classification data，SCD)。单木地上生物量建模数据(biomass modeling data，BMD)是采集时间为2009年6—9月的江西省马尾松解析木数据。马尾松解析木共150株，按照2、4、6、8、12、16、20、26、32和38 cm共10个径阶均匀分配，全部样木均实测胸径、地径和冠幅，将样木伐倒后，测量其树干长度(树高)和活冠长度，分干材、干皮、树枝、树叶称取鲜质量，并分别抽取样品在85 ℃烘干至恒重，根据样品干鲜质量比推算样木地上干质量。估计单木或样地生物量需使用单木胸径和树高，而 SD中没有包括所有样木树高的实测数据，因此SD中剩余未实测的样木树高用BMD数据中的树高和胸径实测数据通过建立树高胸径模型来估计。3种数据的统计特征见表1。

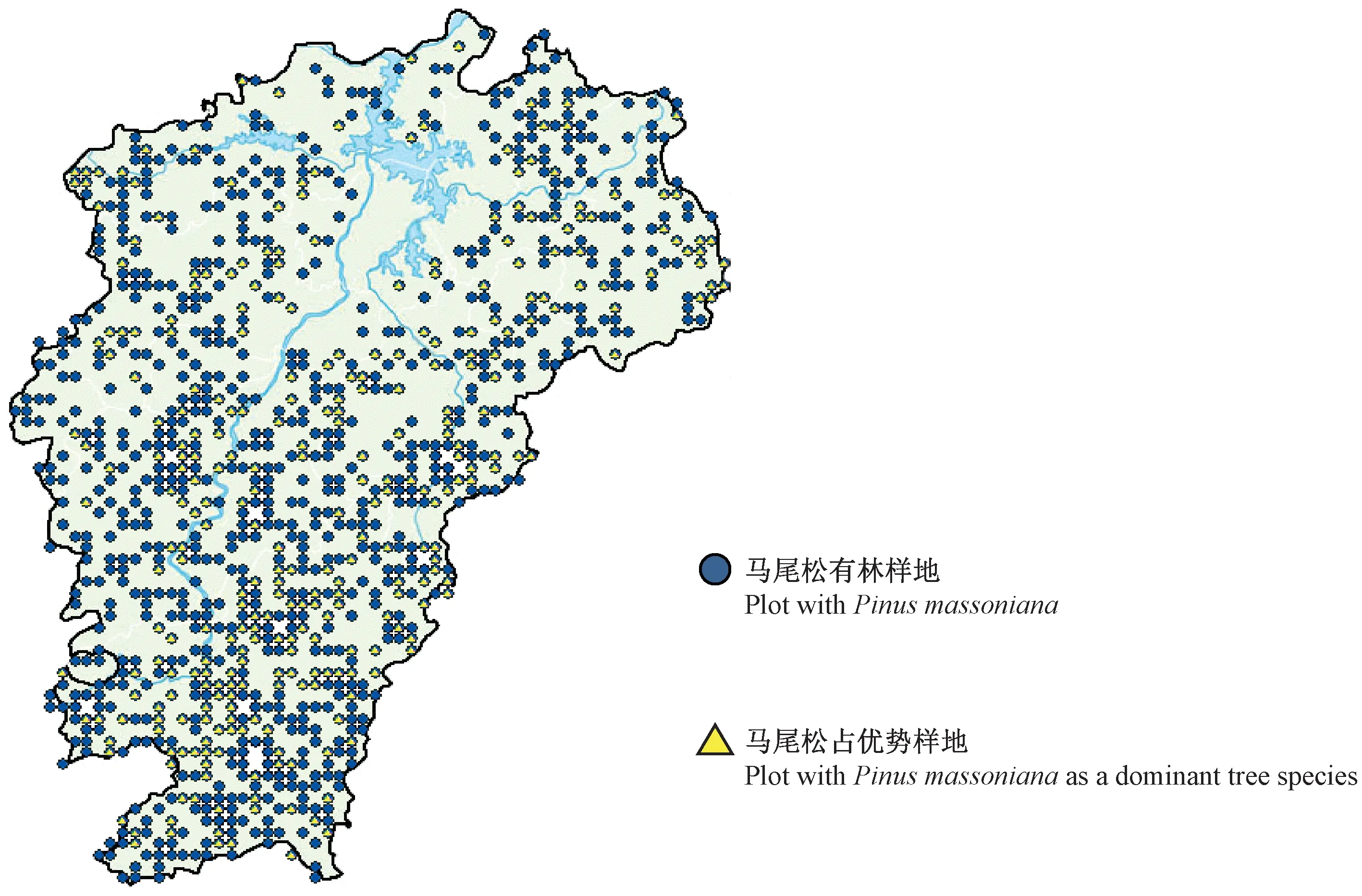
图1 研究区域和样地设置Fig.1 Study region and sample plots set

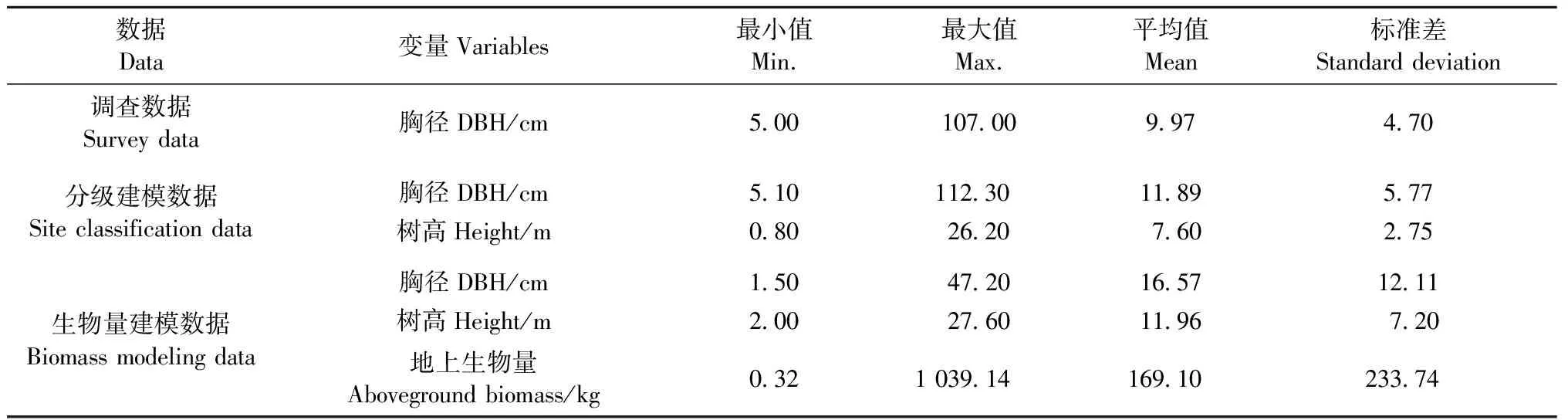
表1 江西省马尾松数据统计特征Tab.1 Descriptive statistics of Pinus massoniana data in Jiangxi Province

2 研究方法

采用异速生长模型形式建立江西省马尾松林单木地上生物量模型，通过树高分级法(Lietal.， 2013)建立马尾松优势木树高-胸径模型获得马尾松优势林样地的立地等级划分，采用蒙特卡洛法(傅煜等，2015)估计区域马尾松优势林的地上生物量和误差，获得区域尺度不同立地等级下的马尾松林地上生物量均值和不确定性估计。单木地上生物量模型和树高分级模型的建立、蒙特卡洛模拟误差估计的过程均通过R软件完成，数据分析和整理用Office Access来实现。

2.1单木地上生物量异速生长模型的建立

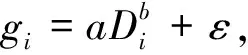
以单木地上生物量为因变量，以BMD中的单木胸径因子或单木胸径因子和树高因子为自变量，采用普通最小二乘法进行拟合，建立3种单木地上生物量估计回归模型：

(1)

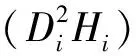
(2)

(3)

式中：gi为第i株单木地上生物量；Di为第i株单木胸径；Hi为第i株单木树高；a、b、c为估计参数；ε为残差。

2.2SD样木的树高估计

建立了单木地上生物量模型之后，结合SD可以估计马尾松单木和样地地上生物量。在估计单木或样地生物量时需要使用单木胸径和树高数据，由于SD中没有包括树高的实测数据，因此本文通过BMD的解析木数据建立树高-胸径模型，结合SD中样木的单木胸径数据来估计单木树高。采用Chapman-Richards公式(4)结合最小二乘法对树高-胸径关系进行拟合：

h=1.3+a(1-e-bd)c+e。

(4)

式中：h为树高；a、b、c为模型参数；d为样木胸径；e为误差。

由于建模样本量较少(150)，因此采用Jackknife法对其参数估计进行检验。

2.3基于优势木树高分级的立地分级

为获得生物量及误差在不同立地条件下的估计，首先要对不同立地质量水平进行划分。由于在大尺度森林清查尤其是在天然混交林分中，年龄数据不但较难获得，而且受空间关系影响使得其与树高关系较弱，因此未采用传统的地位级或地位指数法，而采用优势木树高与胸径的关系来获得立地质量评价(Huangetal., 1993)。在以往的优势木树高-胸径模型中，同一胸径水平下的优势木树高被认为是固定不变的，然而在不同的立地质量条件下，同一胸径水平下的优势木树高是随着立地质量变化的(Lietal.， 2013)。Li等(2013)提出了树高分级法，该方法可将优势木树高与优势木胸径按照不同径阶水平通过迭代分级方法将每一径阶水平下的优势木树高划分为不同的优势木树高等级，大大提高了优势树高与优势木胸径拟合效率，使得优势木树高-胸径模型更好地反映了不同立地质量水平。

为了获得样地水平的立地质量分级，采用树高分级法，利用马尾松优势木树高和优势木胸径的关系进行建模并划分优势木树高等级，用样地优势木树高的等级代表该样地的立地等级。采用Chapman-Richards公式来描述样地中优势木树高与胸径的关系，具体的步骤如下：

1) 将SCD中的胸径数据按照2 cm划分径阶，计算每个径阶下树高最大值和最小值之差，除以要划分的等级数求得级差，在每个径阶内将树高按下式分级：

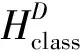
这样，每块样地的每株样木均获得了初始分级。获得初始分级后，确定每个等级下样地的样本容量，若样本容量小于30，则重新确定分级数。

2) 将每个径阶中相同等级的样木数据合并。为了方便起见，使用一个哑变量矩阵来表示每株样木的等级，表示方法如下：

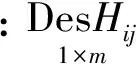
通过下式进行拟合，获得每个等级的模型参数和树高预测值：

(5)

拟合后按照每一等级参数对每株样木树高分别再估算，再按照残差绝对值最小的原则选择估算结果所在的分级对所有样木进行再分级。

3) 重复步骤2，直到各样木分级不再发生变化，得到样木水平的树高分级和分级拟合的曲线。

4) 由于样地面积未超过0.1 hm2，因此规定样地内所有样木均属于同一立地等级。计算样地上每株样木在每条曲线下的预测值，按照残差平方和最小的原则对样地进行重新分级，不断重复这一步骤直到样地分级结果不再发生变化，使得样地上所有样木都获得相同的等级，获得样地水平的树高分级结果。

为获得曲线的最佳拟合效果，在保证每一等级样地样本量(>30)的前提下，尽可能多地划分树高等级。这样将选取的样地划分为5个立地质量等级。

2.4蒙特卡洛法模拟生物量均值及误差估计

蒙特卡洛法是通过反复模拟随机事件的发生过程，并依靠获得这个随机事件在大量试验中的发生频率来估计其概率特征的方法(傅煜等，2015)。通过反复模拟生物量模型的建立和用该模型估计地上生物量的过程，在大量试验中获得生物量估计值和误差的概率分布，得到生物量估计值和误差值的稳定可靠的结果。用单位面积的生物量表示生物量估计值，用均方根误差(RMSE)和相对均方根误差(relative RMSE)表示生物量估计值的误差。具体方法如下：

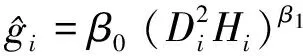
式中：β0、β1、β2为参数；Di为样木胸径；Hi为样木树高。

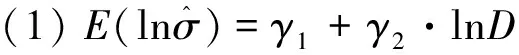
εβ～N[0,exp2(γ1+γ2·lnD)],

(6)

εβ～N[0,exp2(γ1+γ2·lnD+γ3lnH)],

(7)

εβ～N[0,exp2(γ1+γ2·lnD+γ3lnH)]

(8)

的数组来模拟新的残差值εβ，其中式(6)对应式(1)，式(7)对应式(2)，式(8)对应式(3)。

式中：α0、α1、α2为新的参数。

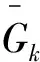
式中：n为立地等级为k时的样地数；f为每块样地的样木株数。

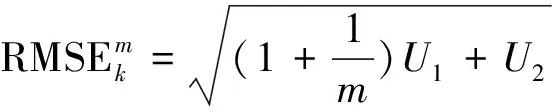
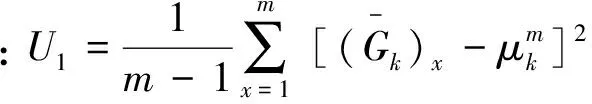
2.5模型评价

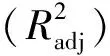
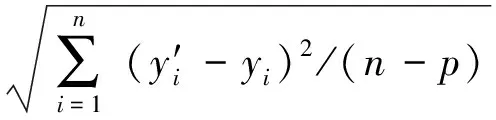
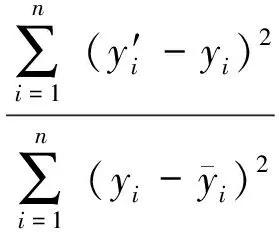
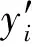
3 结果与分析

3.13种单木地上生物量模型比较

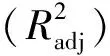
3.2SD样木树高估计

表3给出了用BMD估计的树高-胸径模型(4)的参数估计值、刀切法验证结果及评价指标。刀切法验证的参数估计平均值与全数据估计的参数值相近。模型的R2为0.827，ME为0.026，MAE为2.228，RMSE为0.249，模型拟合效果良好，对SD样木树高估计结果可靠。

3.3优势木树高分级模型与立地分级

用优势木树高等级代替立地等级，表4列出了利用树高分级法建立优势木树高-胸径模型(5)后每条曲线的参数及模型评价指标。其中，a1～a5代表每条曲线的渐近线，即每一立地等级下树高可能达到的最大数值；b是与马尾松生长速度有关的参数；c是表示曲线形状的参数。曲线的R2为0.907，ME为0.001，MAE为0.559，RMSE为0.027，模型拟合效果良好。图2展示了SCD中优势木树高与胸径的关系及进行树高分级建模后拟合的曲线，曲线由下至上分别为第1～5级的拟合结果。SD获得最终分级后每一级的数据统计特征见表5。马尾松优势林各立地等级样地的分布见图3。可以看出，相同立地等级的样地成片分布，相对集中，每一立地等级的样地在江西省全境范围内均有分布。

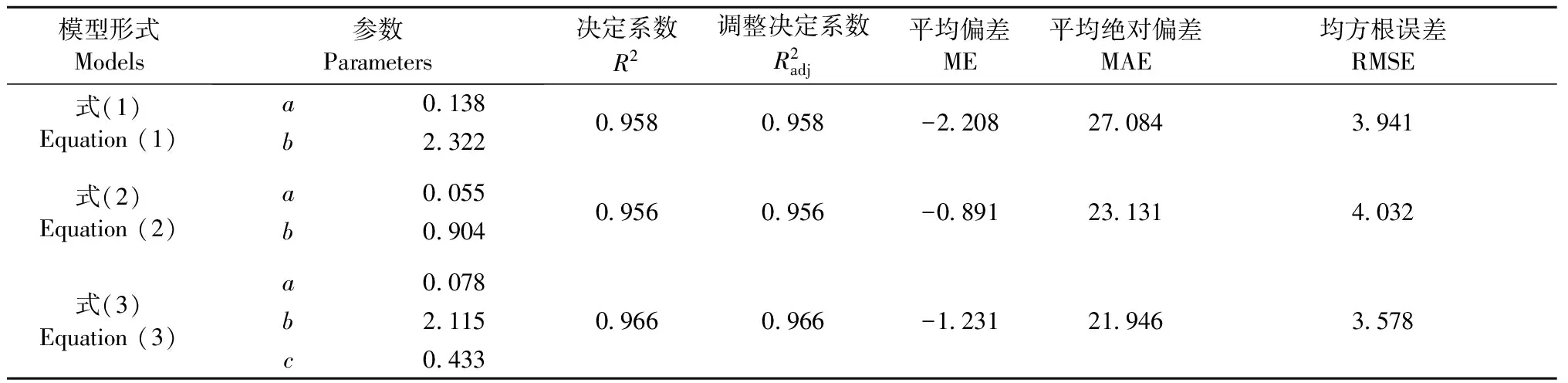
表2 江西省马尾松3种生物量模型建模参数及评价Tab.2 Parameters and its evaluation of the three individual tree biomass models of C.lanceolata aboveground biomass estimation

表3 树高-胸径曲线参数及验证结果Tab.3 Parameters and evaluation of the height-diameter curve fitting

表4 优势木树高-胸径曲线拟合参数Tab.4 Parameters and evaluation of the dominant trees height-diameter curve fitting

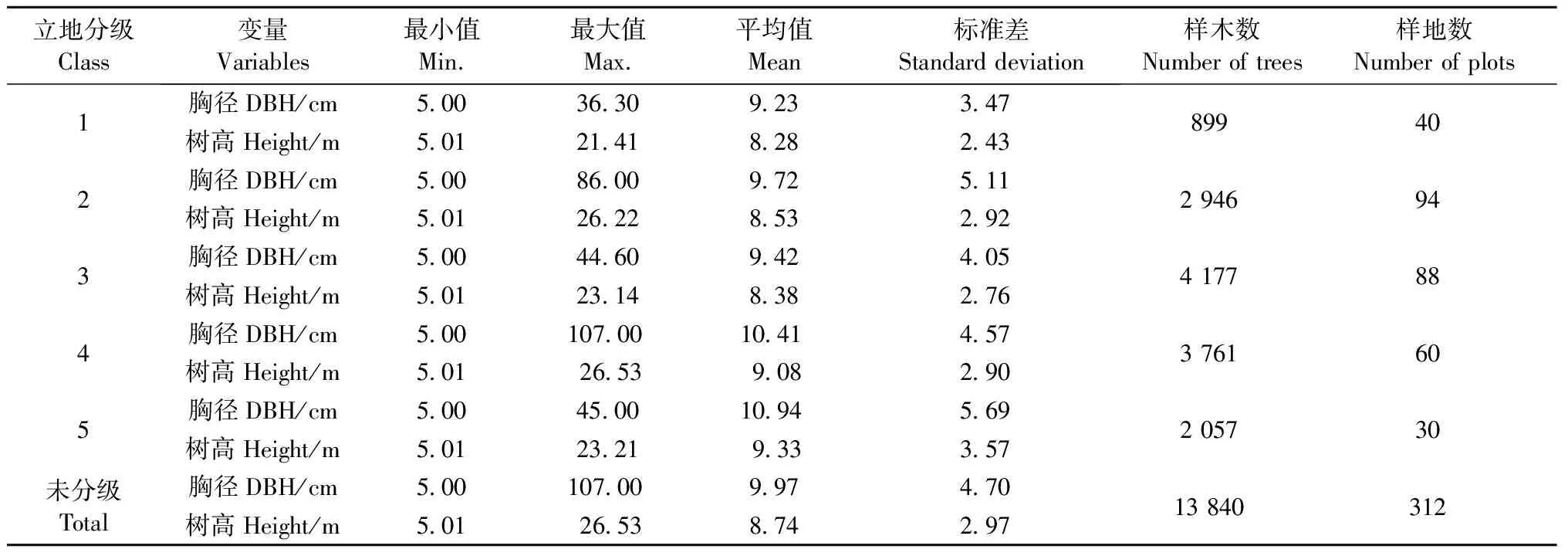
表5 江西省马尾松林立地分级后调查数据的数据特征Tab.5 Descriptive statistics of the P. massoniana forest survey data in Jiangxi Province after site classification

3.3生物量均值与不确定性度量

经对数化处理后，模型残差与胸径或残差与胸径和树高呈现明显的线性关系。在3种生物量模型形式下，生物量残差满足以下特征的正态分布：

ε～N[0,exp2(-3.877+2.281·lnD)];

ε～N[0,exp2(-3.147+1.738·lnD+

0.198·lnH)];

ε～N[0,exp2(-3.432+2.614·lnD+

0.681·lnH)]。

采用蒙特卡洛法对马尾松不同立地等级下3种单木地上生物量模型估计结果及误差进行10 000次模拟的情形见附图1～3，在模拟10 000次的情况下，马尾松地上生物量均值和误差的估计结果均达到了稳定。

图2 优势木树高-胸径拟合曲线Fig.2 Dominant trees height-diameter classification curve

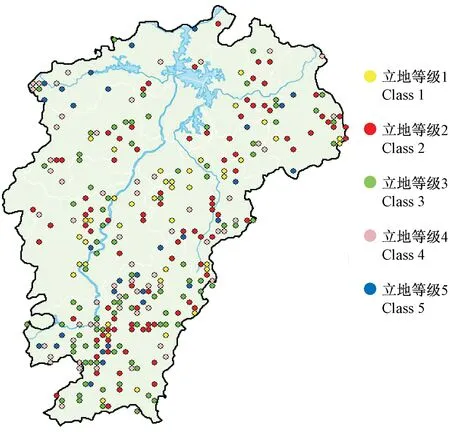
图3 马尾松优势林样地立地分级示意Fig.3 Site quality classes diagram of sample plots with Pinus massoniana as dominant tree species

不同立地等级下3种模型形式地上生物量均值及误差估计结果见表5。在同一单木生物量模型形式下，不同立地等级的地上生物量均值估计结果是不同的，并且随着立地等级的升高而增大。相应的，从相对误差来看，中间立地等级(3级)的误差估计值较小，且有随着立地等级升高或降低而增大的趋势。以式(1)结果为例，地上生物量均值从1级到5级在(9.941±1.804)t·hm-2到(52.845±8.301)t·hm-2之间，随等级升高而增大，第3等级相对误差最小为11.580%。相同立地等级下，3种模型对地上生物量及其误差的估计也有所不同。从生物量均值来看，式(1)>式(3)>式(2)。从绝对误差和相对误差来看，式(2)<式(3)<式(1)，带有树高因子的式(2)和式(3)的相对误差较式(1)更小。例如，未分级情况下，在3种生物量模型的估计中，从式(1)到式(3)的地上生物量均值估计值分别为(26.421±2.539)t·hm-2、(24.525±1.841)t·hm-2和(24.845±2.037)t·hm-2，式(1)的结果最大，式(2)的结果最小；相对误差为9.610%、7.507%、8.199%，式(2)最小，式(1)最大。

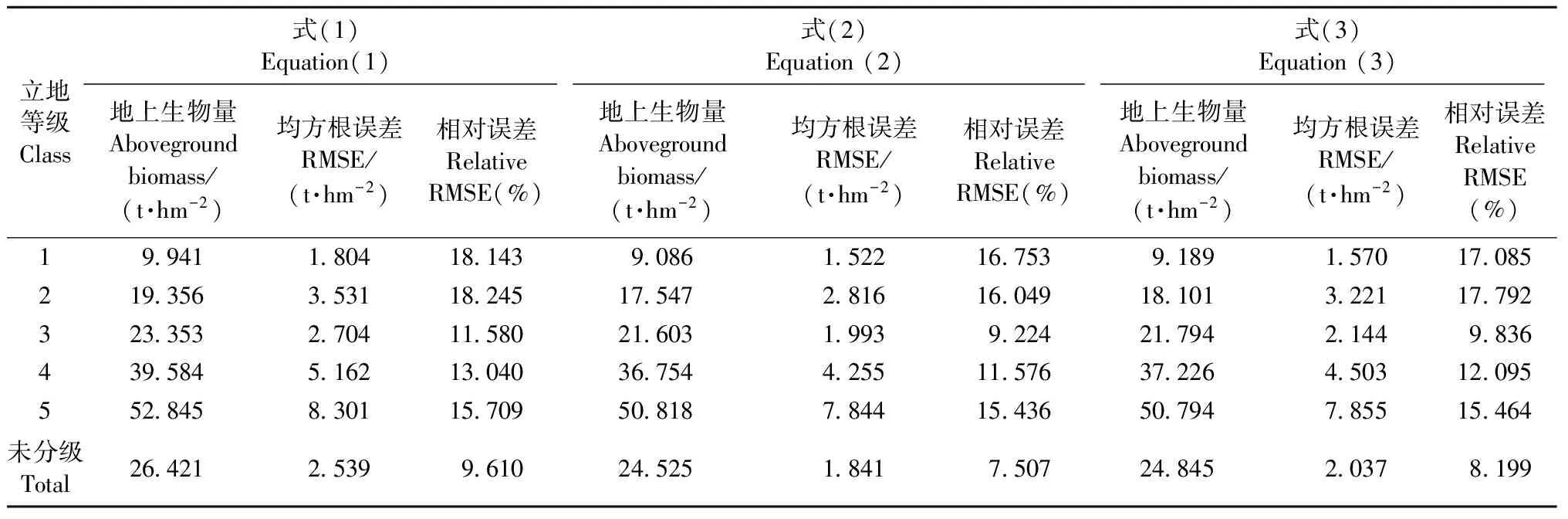
表6 3种模型形式下的不同立地等级江西省马尾松地上生物量均值与不确定性估计Tab.6 Estimates of the regional aboveground biomass per hectare and its uncertainty under three model types in different site classes

4 讨论

从不同立地等级下的生物量估计结果来看，在3种模型形式下，生物量均值有随着立地等级升高而增大的趋势，也就是说立地质量越好，森林生物量密度越大，这也证明了优势木树高分级模型用于立地分级是可行的。中间立地等级(第3等级)代表着立地质量的平均水平，由表5可以看出，立地平均水平的生物量估计误差最小，而且生物量估计结果更接近总体水平，立地质量越接近平均水平，生物量估计的相对误差越小，这说明模型分级效果很好，采用优势木树高分级来划分立地等级是可靠的。

从单木水平、样地水平再到区域水平，不确定性普遍存在于生物量估测的各个阶段(Cohenetal.,2013)。在推算单木生物量时，主要的不确定性来源有2方面，即作为模型变量的各种测树因子的测量误差以及包括模型选择误差和参数估计误差在内的单木生物量模型误差(Chaveetal.， 2004；McRoberts，1996； Ståhletal., 2011)。从单木推算到区域尺度生物量时，不确定性的来源还包括抽样误差以及由单木生物量估计模型外推时传播并累积下来的测量和模型误差(Chaveetal.， 2004)。在同一次调查中，样木测树因子的测量误差与样地选择的抽样误差的分布基本上是稳定的，而由立地质量不同导致的生物量模型估计误差就成了不确定性的主要来源。因此，在同一生物量模型形式下，不同立地等级间生物量均值相对误差的差异主要是由于立地质量差异造成的；而相同立地等级时不同模型形式间生物量均值相对误差的差异主要是模型形式差异所导致。在实际应用中，选择合适的模型对不同区域不同立地质量的生物量进行估计对提高估计精度十分重要。

本研究利用优势木树高分级数据(SCD)建立了立地分级曲线，在建立生物量模型时使用的是伐倒后测量的生物量实测数据，2套数据是独立的，因此对立地分级时建立树高胸径模型引起的误差以及建立生物量模型使用的树高估计值的误差并不在讨论之列。在以往的区域森林地上生物量估计中，一般只得到一个区域的总体生物量估计结果，往往忽略了生物量在不同立地条件下的分布，更无从知晓估计误差在不同立地条件下的情况。本文用优势木树高分级代替立地分级，对区域立地质量进行划分，并结合估计不同立地等级的生物量均值及误差来选择合适的模型形式，提出了精准估计不同立地条件下森林生物量的一种新思路，对森林经营管理和制定决策方案具有重要意义。未来可将这种方法推广到不同区域和不同的树种中去，结合多期调查数据，为精准估计不同立地质量的森林立地生产力提供技术支持和参考。

5 结论

3种单木地上生物量模型形式下的马尾松地上生物量估计结果相比，加入树高变量的式(2)和式(3)生物量估计误差的绝对值和相对值均好于式(1)，加入树高变量的单木生物量模型能够提高估计精度。在胸径和树高2种变量同时存在时，拥有2个参数的式(2)较有3个参数的式(3)获得了更好的估计效果。

从不同立地等级生物量估计结果和误差来看，立地平均水平，即中间立地等级的误差最小，立地质量越接近平均水平，生物量估计的相对误差越小。

不同立地等级的区域马尾松优势林地上生物量均值随着立地质量水平提高而增大，即立地质量越高，森林生物量密度越大，证明了优势木树高分级用作划分立地等级依据的可行性。

通过用优势木树高分级代替立地等级的方法，可以获得样地水平立地质量的划分，结合蒙特卡洛模拟法，可以得到不同立地等级下生物量均值及其误差的估计，这使得生物量的估计结果更加细化，为精准估计不同立地质量的森林生物量提供技术支持，进而为精准估计森林立地生产力提供参考。

傅 煜, 雷渊才, 曾伟生. 2015. 单木生物量模型估计区域尺度生物量的不确定性. 生态学报, 35(23): 7738-7747.

(Fu Y, Lei Y C, Zeng W S. 2015. Uncertainty analysis forregional-level above-ground biomass estimates based on individual tree biomass model. Acta Ecologica Sinica, 35(23): 7738-7747.[in Chinese])

李海奎, 雷渊才. 2010.中国森林植被生物量与碳储量评估. 北京： 中国林业出版社.

(Li H K, Lei Y C. Estimation and evaluation of forest biomass carbon storage in China. Beijing: China Forestry Publishing House.[in Chinese])

曾伟生. 2014. 3 种异速生长方程对生物量建模的对比分析. 中南林业调查规划, 33(1): 1-3.

(Zeng W S. 2014. Comparison of three allometric equations for biomass modeling. Central south forest inventory and planning, 33(1):1-3,19.[in Chinese])

Berrill J P, O’Hara K L. 2013. Estimating site productivity in irregular stand structures by indexing the basal area or volume increment of the dominant species. Canadian Journal of Forest Research, 44(1): 92-100.

Chave J, Condit R, Aguilar S,etal. 2004. Error propagation and scaling for tropical forest biomass estimates. Philosophical Transactions of the Royal Society of London B: Biological Sciences, 359(1443): 409-420.

Cohen R, Kaino J, Okello J A,etal. 2013. Propagating uncertainty to estmates of above-ground biomass for Kenyan mangroves:a scaling procedure from tree to landscape level.Forest Ecology and Management,310:968-982.

Cole T G, Ewel J J. 2006. Allometric equations for four valuable tropical tree species. Forest Ecology and Management, 229(1): 351-360.

Fang J, Chen A, Peng C,etal. 2001. Changes in forest biomass carbon storage in China between 1949 and 1998. Science, 292(5525): 2320-2322.

Gargaglione V, Peri P L, Rubio G. 2010. Allometric relations for biomass partitioning ofNothofagusantarcticatrees of different crown classes over a site quality gradient. Forest Ecology and Management, 259(6): 1118-1126.

Huang S, Titus S J. 1993. An index of site productivity foruneven-aged or mixed-species stands. Canadian Journal of Forest Research, 23(3): 558-562.

Ketterings Q M, Coe R, van Noordwijk M,etal. 2001. Reducing uncertainty in the use of allometric biomass equations for predicting above-ground tree biomass in mixed secondary forests. Forest Ecology and Management, 146(1): 199-209.

Li H, Zhao P. 2013. Improving the accuracy oftree-level aboveground biomass equations with height classification at a large regional scale. Forest Ecology and Management, 289: 153-163.

McRoberts R E. 1996. Estimating variation in field crew estimates of site index. Canadian journal of forest research, 26(4): 560-565.

McRoberts R E, Westfall J A. 2014. Effects of uncertainty in model predictions of individual tree volume on large area volume estimates. Forest Science, 60(1): 34-42.

Pérez-Cruzado C, Rodríguez-Soalleiro R. 2011.Improvement in accuracy of aboveground biomass estimation inEucalyptusnitensplantations: effect of bole sampling intensity and explanatory variables. Forest Ecology and Management, 261(11): 2016-2028.

Peri P L, Gargaglione V, Pastur G M,etal. 2010. Carbon accumulation along a stand development sequence ofNothofagusantarcticaforests across a gradient in site quality in Southern Patagonia. Forest Ecology and Management, 260(2): 229-237.

Petersson H, Holm S, Ståhl G,etal. 2012. Individual tree biomass equations or biomass expansion factors for assessment of carbon stock changes in living biomass—a comparative study. Forest Ecology and Management, 270: 78-84.

Rock J. 2007. Suitability of published biomass equations for aspen in Central Europe—results from a case study.Biomass and Bioenergy,31(5):299-307.

Satoo T, Madgwick H A I. 1982. Biomass∥Madgwick H A I. Forest biomass. Netherlands: Springer, 46-89.

Skovsgaard J P, Vanclay J K. 2008. Forest site productivity: a review of the evolution of dendrometric concepts for even-aged stands. Forestry, 81(1): 13-31.

Ståhl G, Holm S, Gregoire T G,etal. 2011. Model-based inference for biomass estimation in a LiDAR sample survey in Hedmark County, Norway. Canadian Journal of Forest Research, 41(1):96-107.

Wang C. 2006. Biomass allometric equations for 10 co-occurring tree species in Chinese temperate forests. Forest Ecology and Management, 222(1): 9-16.

(责任编辑 石红青)

BiomassandUncertaintyEstimatesofPinusmassonianaForestforDifferentSiteClassesinJiangxiProvince

Zhao Han Lei Yuancai Fu Liyong

(ResearchInstituteofForestResourceInformationTechniques,CAFBeijing100091)

附图1 基于式(1)的区域不同立地条件下马尾松林生物量与误差估计在蒙特卡洛模拟10 000次下的结果Attached fig.1 The status using Monte Carlo method simulated 10 000 times to estimate the regional tree aboveground biomass and its uncertainty with equation (1) at 5 site classes

附图2 基于式(2)的区域不同立地条件下马尾松林生物量与误差估计在蒙特卡洛模拟10 000次下的结果Attached fig.2 The status using Monte Carlo method simulated 10 000 times to estimate the regional tree aboveground biomass and its uncertainty with equation (2) at 5 site classes

附图3 基于式(3)的区域不同立地条件下马尾松林生物量与误差估计在蒙特卡洛模拟10 000次下的结果Attached fig.3 The status using Monte Carlo method simulated 10 000 times to estimate the regional tree aboveground biomass and its uncertainty with equation (3) at 5 site classes

S757

A

1001-7488(2017)08-0081-13

10.11707/j.1001-7488.20170810

2016-03-04；

2016-04-22。

中央级公益性科研院所基本科研业务费专项资金重点项目“基于轻小型无人机平台的多尺度森林生物量估计”(CAFYBB2016SZ003)； 国家自然科学基金项目(31170588，31570628,31300534)。

*雷渊才为通讯作者。感谢国家林业局调查规划设计院曾伟生教授级高工提供的马尾松解析木数据。