带阶梯型谐振腔的Hartmann低频超声雾化喷嘴设计及试验

高建民，马俊龙



带阶梯型谐振腔的Hartmann低频超声雾化喷嘴设计及试验

高建民，马俊龙

（江苏大学现代农业装备与技术教育部重点实验室，镇江 212013）

针对目前雾化栽培领域所用喷嘴无法兼具雾滴粒径细小及大雾化量特性的问题，该文设计了一种带阶梯型谐振腔的流体动力式Hartmann低频超声雾化喷嘴，为了使喷嘴喷雾方向可控，对雾化区域进行了流场主动控制，即在喷雾出口区域设置了圆锥罩，通过数值模拟研究了小尺寸阶梯型谐振腔的振动特性，对其雾化效果进行了试验对比。结果表明：在相同参数条件下，当阶梯型谐振腔第二级阶梯孔与第一级阶梯孔深度比超过2时，其谐振频率达到了传统圆柱型谐振腔谐振频率的1.6～1.7倍；圆锥罩的加入使得腔内流体压力振幅变大，初段起振特性更优；阶梯型谐振腔两级阶梯孔孔径比是影响阶梯腔谐振特性的重要因素，阶梯孔孔径比的改变会使阶梯型谐振腔的谐振模式由“回流模式”转变为“尖声模式”或使谐振现象消失；带阶梯型腔体的低频超声雾化喷嘴比带普通圆柱型腔体喷嘴的雾化效果更好，在0.1 MPa～ 0.5 MPa的进气压力下，前者比后者雾滴粒径小2～6m；阶梯型谐振腔式超声雾化喷嘴在加装圆锥罩之后，低压时的雾滴粒径随供气压力变化更大，而在高压时，其雾化效果与没有加装圆锥罩的阶梯型谐振腔式超声雾化喷嘴相比基本一致；索太尔平均粒径SMD（Sauter mean diameter）随Laval管出口与谐振腔之间的距离的变大呈现出先变小后变大的趋势，SMD的变化趋势与腔内声压级SPL的变化趋势基本一致。雾化量为2 L/h下时，阶梯腔式超声雾化喷嘴的最小雾滴粒径为42m。该研究可为阶梯腔式超声雾化喷嘴在雾化栽培领域的应用提供参考。

喷嘴；数值模拟；喷雾；试验；Hartmann低频超声雾化；阶梯型谐振腔；圆锥罩

0 引 言

目前雾化栽培使用的喷嘴主要有压电超声式和机械式（如压力雾化、旋转雾化、离心雾化）2大类。压电式超声雾化喷嘴生成的雾滴细小均匀，但是其雾化量偏小，只适用于小规模雾化栽培。机械式雾化喷嘴的雾化量虽然大，但是其生成的雾滴粒径偏大并且均匀性较差。因此，研制雾化量大且生成的雾滴细小均匀的喷嘴，是大规模雾化栽培的当务之急。

1919年，Hartmann在做皮托管测压试验时，他发现将头部为半球型中心部位开有测压孔的皮托管放置在超音速流场中的某些区域时，管内会产生像正弦波一样的压力脉动[1]。自此，国内外学者对Hartmann tube（HT）的谐振机理、声场特性及热效应做了大量的研究[2-7]。HT结构简单，本身没有运动部件却能够产生高达20 kHz的高频振动，被应用于超声雾化、抑制噪声、声波除尘等各个领域。谐振腔的振动状态与射流参数及腔体的几何形状有着密切的联系[8-9]。Sarohia等[10]研究表明，在不同的参数下谐振腔工作在3种不同的模式下，分别是：回流模式、不稳定模式和尖声模式。Masaaki Kawahashi 等[11]首次参数化研究了单阶梯型谐振腔两段阶梯孔直径比以及深度比对谐振腔振动频率的影响。Raman等[12]通过试验的方法研究了阶梯型谐振腔的震荡特性及热力学特性。之前学者关于阶梯型谐振腔的研究主要是试验研究。近年来国内外学者对于圆柱腔型哈特曼雾化喷嘴在石油工业、航空航天、粉末冶金等热喷雾领域的应用做了相关研究[13-19]，但是冷喷雾效果不佳。以作者所掌握的资料，目前对于带阶梯型谐振腔的流体动力式低频超声雾化喷嘴的研究未见之于公开文献。鉴于此，本文拟设计一种带阶梯型谐振腔的Hartmann低频超声雾化喷嘴，以满足大规模雾化栽培的需求。通过CFD数值模拟的方法[20-23]对阶梯型谐振腔的声场特性进行了研究，并试验研究了该喷嘴的雾化特性。

1 带阶梯型谐振腔的Hartmann低频超声雾化喷嘴设计

根据流体动力式谐振腔振动原理[24-28]，设计出了如图1a所示的带阶梯型谐振腔的Hartmann低频超声雾化喷嘴。其雾化机理为，亚音速的高压气体由喷嘴尾部进入喷嘴，经过Laval喷嘴后，气流被加速到超音速，气流在靠近Laval管出口处与液流汇合，并对液流造成猛烈冲击，使液流破碎分裂，发生第一次雾化。与此同时，高速气流撞击阶梯型谐振腔后发生高频振动，大液滴在高强度声场内被进一步振裂细化，雾滴粒径进一步变小，粒径分布也更加均匀。二相流环境中，考虑雾滴只受气动力和表面张力的作用，雾滴颗粒在破碎临界点的带修正因子临界韦伯数[29]为

（2）

2 数值模拟

2.1 物理模型及数值计算方法

简化物理模型后，建立了如图1 b、1c中所示的二维轴对称流体模型区域，其中图1b是无圆锥罩模型，图1c是含有圆锥罩模型。

网格划分在Ansys14.0软件中完成，网格采用四边形非结构网格，采用高级网格尺寸函数，控制方法为Proximity and Curvature，以2=21的无圆锥罩模型为例，在拉瓦尔管区域及阶梯腔区域最小网格尺寸为0.075 mm，而其他区域最小网格尺寸为0.15 mm，网格数量为10 773。数值模拟在Fluent软件中进行，使用密度基显式求解器，近壁面处理方法采用standard wall functions，标准大气压力101 325 Pa，空气温度300 K。

2.2 数值模型及时间步长可靠性验证

湍流模型在一定程度上影响压力震荡波形，Realizable模型可以更好地模拟射流撞击、旋流、二次流、圆孔射流等复杂流动，所以本文所有数值模拟均使用Realizable-模型。笔者经过大量的数值模拟计算后，发现时间步长的选择对数值模拟结果会造成较大的影响，为此，根据本文流体模型最小网格尺寸（0.075 mm），以及预估流体最大速度680 m/s至1 360 m/s，选定3个时间步长（timestep）：2e-7 s、2.5e-7 s和3e-7 s进行可靠性验证。所使用的腔体模型为传统圆柱型腔体，即使本文阶梯型腔体1=2即可。另外，2=21，=1.40o，in= 0.3 MPa，得出压力震荡波形及频谱图如图2所示。监测点坐标（3,0,0），坐标原点为阶梯腔入口截面与轴线交点。以时间步长2e-7s为例，得到监测点'压力的震荡频率为6.746 kHz，压力振幅为1.978´105Pa。传统基于线性声学理论的频率计算公式为：=/4（+0.3），其中、、分别为当地声速（m/s）、谐振腔深度（m）、谐振腔直径（m）。由Brocher提出的最大压力振幅公式[30]： Δmax= 2j0，其中Δmax为最大压力波动幅度（Pa），为绝热指数，取值1.414，j为射流马赫数，j=0.82,0为标准大气压（Pa）。由此得出的频率为6.787 kHz，压力振幅为2.329´105Pa。可以看出监测点震荡频率与传统理论公式得出结果基本一致，而压力振幅却比Brocher提出的公式得出的结果略低，但考虑到此公式是适用于理想条件下，而没有考虑壁面摩擦损失等因素，因此该模拟结果是可以接受的。

a. 带阶梯型谐振腔的Hartmann超声雾化喷嘴结构示意图

a. Schematic diagram of Hartmann ultrasonic atomization nozzle with stepped resonance tube

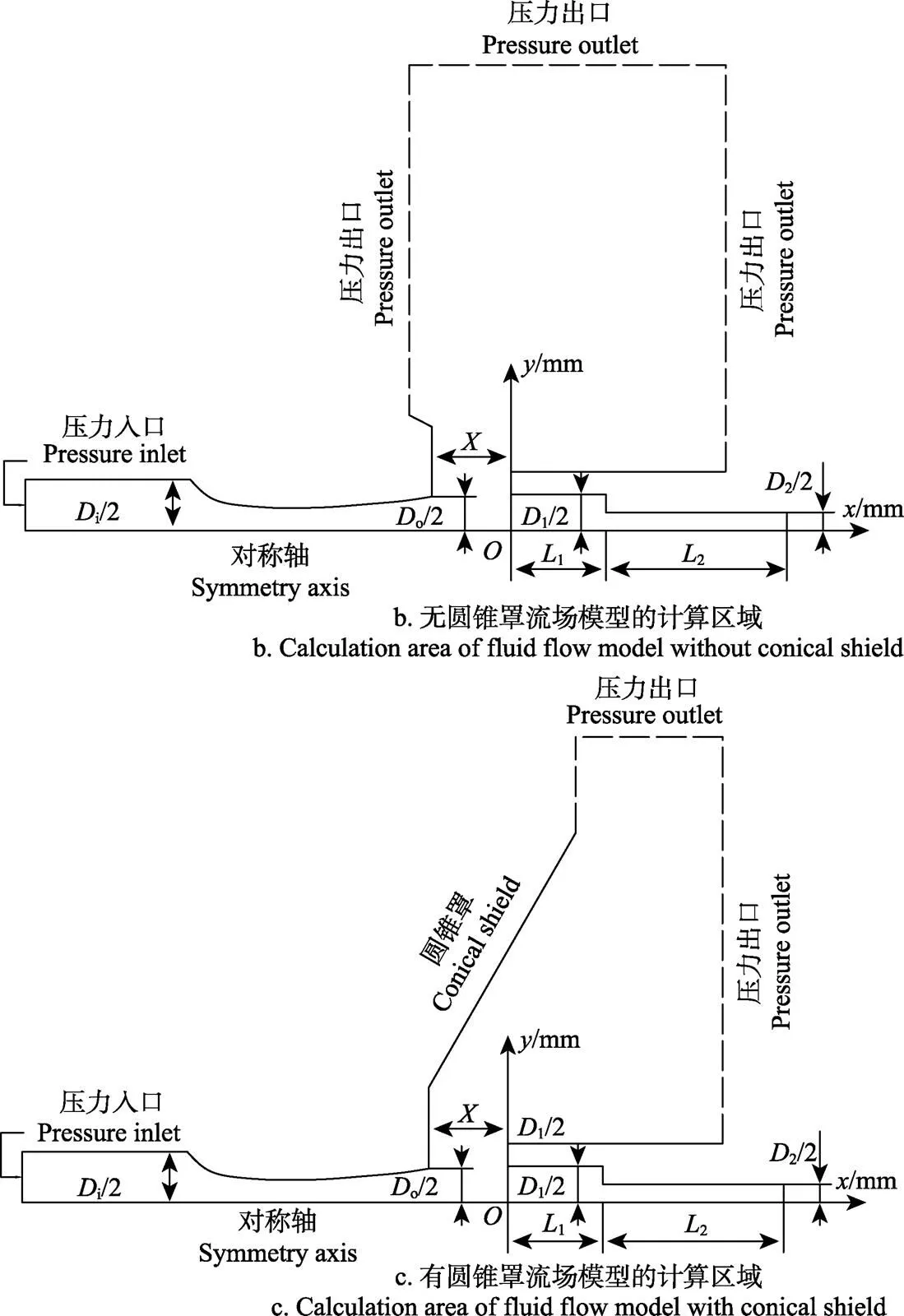
注：Di为Laval管的入流直径，mm；Do为Laval管出流直径，mm；D1为阶梯型谐振腔第一级阶梯孔的直径，mm；D2是阶梯型谐振腔第二级阶梯孔的直径，mm；L1为第一级阶梯孔的深度，mm；L2是第二级阶梯孔的深度，mm；X为Laval管出口与谐振腔之间的距离，mm。

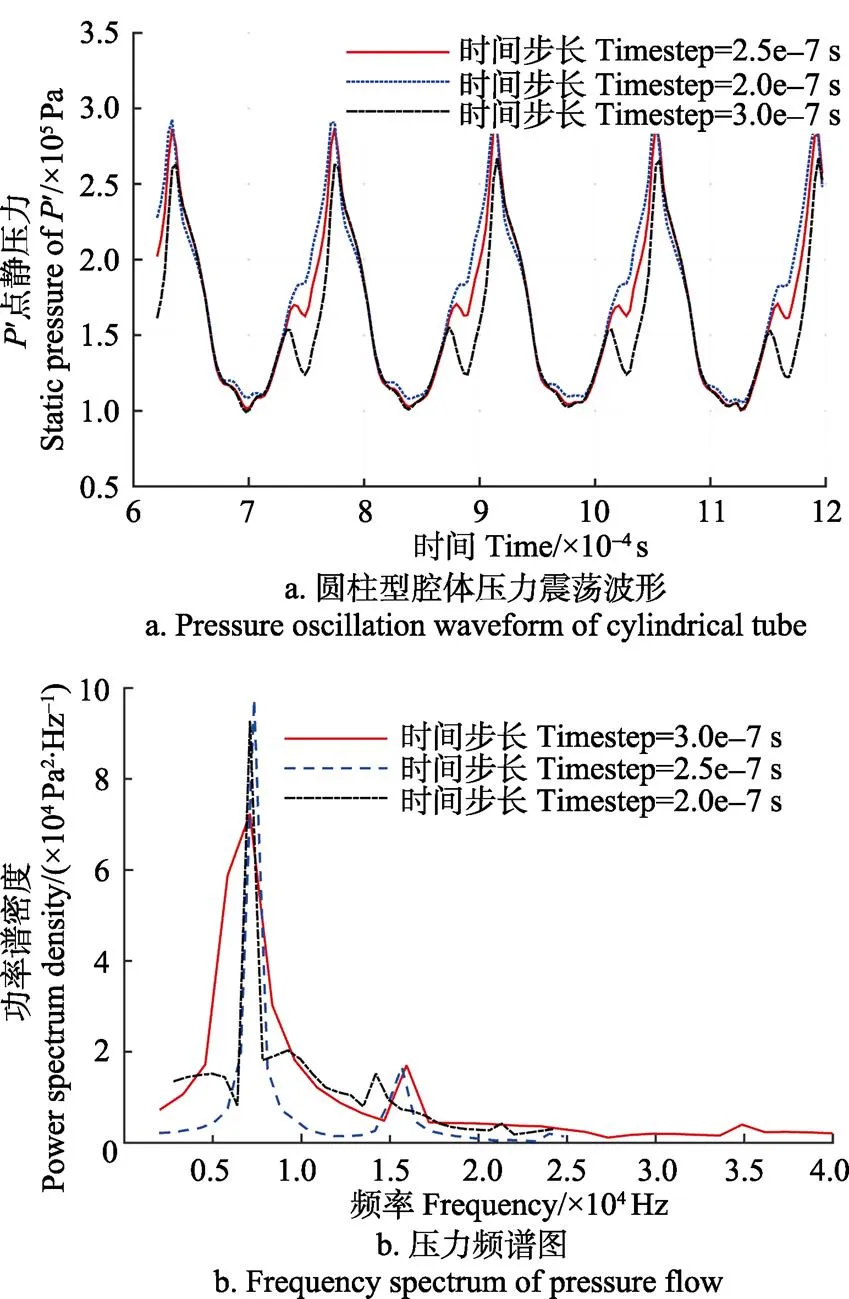
注：P'（3,0,0），坐标系见图1。

在Fluent瞬态求解中时间步长（timestep）必须小到能够解析与时间相关的一切特征，而影响时间步长设置值的最直接因素是网格尺寸以及射流流速，而在上述可靠性验证过程中所使用的圆柱腔型谐振腔模型与本文所主要研究的阶梯腔型超声雾化喷嘴模型基本尺寸一致，最小网格尺寸以及网格划分方法相同，且射流速度相同。因此以上对于圆柱腔喷嘴模型的验证结果同样适用于阶梯腔型超声雾化喷嘴模型。对比3个时间步长的计算结果，其压力时域图及频谱图基本一致，时间步长为2.5e-7 s和3e-7 s时的平均压力振幅与2.0e-7 s时相比相对误差分别为0.41%和0.36%；而平均谐振主频的相对误差分别为0.03%和0.12%。为节省计算时间又不失计算精度，下文对于各参数对振动腔振动特性和谐振状态的所有模拟，计算时间步长均采用2.5e-7 s。

3 数值模拟结果与分析

3.1 阶梯孔深度比2/1对谐振状态的影响

Laval管出口直径o为定值3.1 mm，令谐振腔入口直径1等于Laval管出口直径相等即3.1 mm，1/2=2。为使阶梯型谐振腔腔体为细长孔形状，使第一级阶梯孔深度1略大于第一级阶梯孔直径，设定1=4 mm。2分别取值为4、8、12、16、20 mm。且初定=1.40o，供气压力in=0.3 MPa。在无圆锥罩情况下进行瞬态数值模拟，最后得到其稳定状态的点的压力图和其对应的频谱图如图3a和3b所示，其中点坐标（3,0,0），坐标原点为阶梯腔入口截面与轴线交点。在表1中，对于圆柱型腔体，2/1变化时指代的是圆柱腔深度的变化，即圆柱腔的深度等于2+1。结果表明，在相同参数条件下，当谐振腔的总深度相等时，阶梯型共振腔的谐振频率比传统圆柱型谐振腔的谐振频率高。由表1可以看出，当阶梯型谐振腔2/1超过2时其谐振频率即达到了传统圆柱型谐振腔谐振频率的1.6倍。

Note: D1/D2=2, X=1.40Do, D1 =Do, L1=4 mm, Pin=0.3 MPa

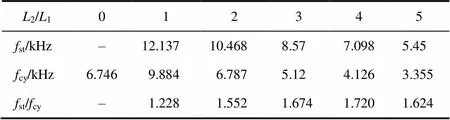
表1 当L2/L1变化时阶梯腔（fst）和圆柱腔（fcy）谐振频率对比

注：圆柱腔与同一条件下的阶梯腔深度一致。

Note: The depth of cylindrical tube agrees with that of the stepped tube under the same condition.

3.2 圆锥罩对谐振状态的影响

如前文所述，为了对流体的流动状态施加主动控制，本文中在拉瓦尔管出口和谐振腔入口之间加装了120°圆锥罩，如图2b所示。在与无圆锥罩时相同的参数下，即212，=1.40o，122，1=o，1=4 mm，in= 0.3 MPa，对点静压力进行了数值模拟。结果表明，其最大压力波动幅度却由无圆锥罩时的0.103 MPa增大至0.174 MPa。如图4所示，有圆锥罩时，其压力波形图出现了多处锯齿状的跳跃。为了对其内部流场波动情况做进一步的探究，分别取一个周期中的4个点1=7.48e–4 s，2=7.63e–4 s，3=7.88e–4 s，4=8.30e–4 s，观察其速度矢量图在1至4过程的演变过程。其结果如图5所示，在1时刻，此时腔内气体处于出流阶段，在圆锥罩转角部分形成了一个涡流，而达到2时刻时，此涡流消失，而与此同时在阶梯腔的第一段阶梯孔内渐渐形成了一个涡流，第一个阶梯孔内的涡流直径逐渐变大，最终充满整个阶梯孔，此时第二段阶梯孔的气体处于静止状态，此后即进入入流阶段，涡流直径又逐渐变小直至消失，即3时刻，阶梯腔出口和圆锥罩之间又形成了新的涡流，其位置更靠近阶梯腔出口一侧，最终入流阶段完成，即3时刻。由此我们可以看出，圆锥罩与阶梯腔出口之间的涡流形成与消失的过程中，会对腔内气体的入流和出流造成周期性的扰动，从而使得波形图上显现出锯齿状的跳跃，同时也使得腔内气体振动幅度变大，增大了其压力波动幅度。

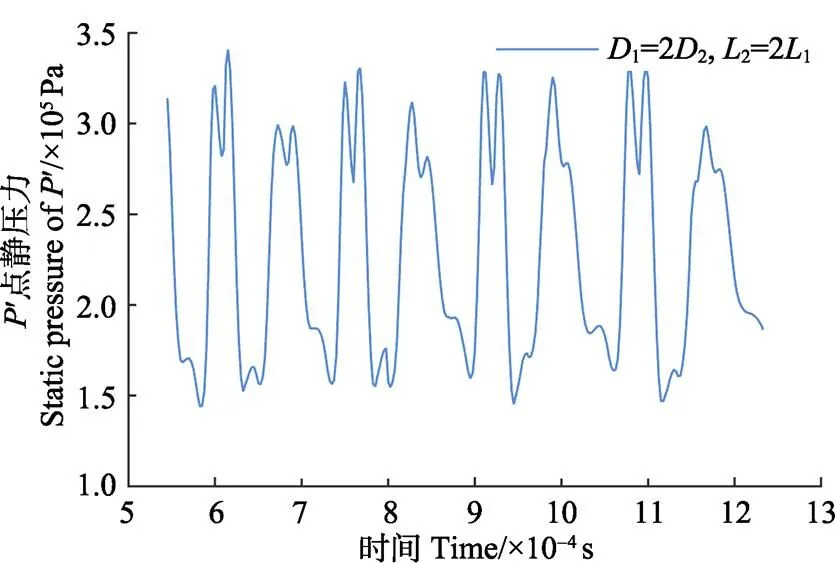
Note: L2/L1=2, X=1.40Do, D1/D2=2, D1 =Do, L1=4 mm, Pin=0.3 MPa.

图5 带圆锥罩的谐振腔在一个周期内速度矢量图演变过程

3.3 阶梯孔孔径比1/2对谐振状态的影响

如图6所示，本文在对不同孔径比1/2对谐振状态影响的数值模拟过程中发现孔径比是影响阶梯腔谐振状态比较敏感的因素，在1/2小于1.2的情况下，阶梯腔和传统圆柱腔的效果基本一致。而当1为定值，在1=o，=1.40o，in=0.3 MPa，2=21的参数条件下，当1/2由2增大到2.5时，阶梯型谐振腔的谐振状态由“回流模式”转变为“尖声模式”。在这种谐振模式下其压力震荡没有典型的规律，很难找到起主要作用的主频，而更像是多种不同振幅和频率的复杂的波叠加在一起的效果。当1/2继续增大至3，即2小于0.44o时，就很难再观察到波动现象，压力波动经过初始的不稳定阶段后逐渐趋于某一定值。

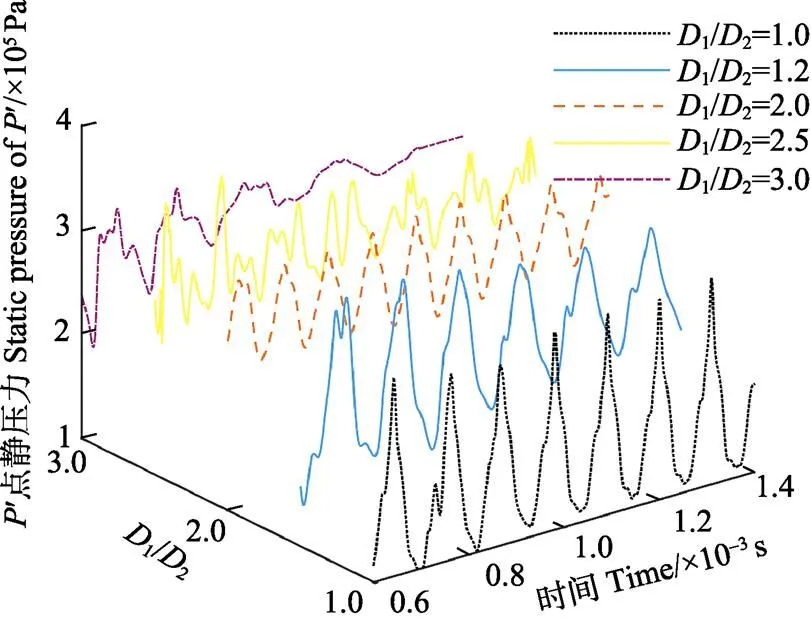
Note: L2/L1=2, X=1.40Do, D1 =Do, L1=4 mm, Pin=0.3 MPa

3.4 Laval管出口与谐振腔之间的距离对谐振状态的影响

在2/12，1/22，1=o，1=4 mm，in=0.3 MPa的固定参数条件，变化时进行数值模拟。结果如图7所示，当在5～11 mm范围内的任意位置，谐振腔均可产生持续稳定的回流模式的震荡，且其主频不受变化的影响，'点压力震荡主频约为10.5 kHz。为了进一步探究当变化时阶梯型谐振腔谐振状态的变化情况，由数值模拟结果得出变化时第一阶梯孔轴线上点声压级SPL及最大静压力max的变化情况，如表2所示。可以看出随着的变大点的声压级SPL呈现出先由75.5 dB急剧变大，后趋于稳定（90~110 dB），又急剧变小为 69.6 dB的趋势，此过程伴随着腔内流体回流谐振现象的产生与消失。而在此变化范围内，点最大静压力max由2.98´105Pa逐渐变小为2.82´105Pa。

由数值模拟的结果表明，阶梯孔的深度比2/1对阶梯腔的谐振频率有直接影响，2/1取值接近于1时，阶梯型谐振腔的谐振频率达到最大值；而阶梯型谐振腔两级阶梯孔孔径比1/2对谐振腔的谐振状态有较大影响，能产生稳定回流模式谐振的1/2范围为1.2～2；Laval管出口与谐振腔之间的距离的较佳工作范围为 5～9 mm，在此范围内谐振腔均能达到稳定的谐振状态，监测点¢的声压级SPL达到了100 dB左右。根据以上数值模拟结果，最终选用较优设计参数1/2=2进行阶梯腔喷头试制，并选用较优的拉瓦尔管与谐振腔距离= 5.5 mm作为喷雾特性对比测试试验的初始结构参数值。

Note:L2/L1=2, D1/D2=2, D1 =Do, L1=4 mm, Pin=0.3 MPa.

表2 P'点最大静压力Pmax及声压级SPL随X变化情况

Note:212,1/22,1=o,1=4 mm,in=0.3 Mpa

4 雾滴粒径对比测试试验

4.1 试验设备及试验方案

为了对本文所设计的带阶梯型谐振腔的Hartmann低频超声雾化喷嘴的雾化性能做进一步了解，试制喷嘴样机对不同结构型式的喷嘴在不同供气压力in（MPa）下进行雾滴粒径对比测试试验，分别对带有普通圆柱腔、阶梯腔、带有圆锥罩的阶梯腔的3种Hartmann雾化喷嘴进行对比试验，测试其在不同压力下的索太尔平均粒径（Sauter mean diameter，SMD）的变化情况，其中阶梯腔的阶梯深度比为定值2=1，Laval管出口与谐振腔之间的距离1.77o；并分别以、2/1等因素为变量进行了雾滴粒径测试试验。1、2、1为定值，其中1=o，1=22，1=1.33o(各参数取值与仿真模型一致)，如图1和图2所示，通过调整调节柱塞使得可调节2/1的值。本次试验在江苏大学农业装备工程学院雾化试验室进行，气温为27～29 ℃。

带阶梯型谐振腔的Hartmann低频超声雾化喷嘴雾滴粒径谱测试装置如图8所示，试验控制系统由水路系统与气路系统组成，水路系统包括隔膜水泵9（型号PLD- 1 204，石家庄市普兰迪机电设备有限公司）、水泵调速器8（型号15C，石家庄市普兰迪机电设备有限公司）、节流阀10（型号KC-02，上海阮隆工业自动化电器有限公司）、液压表11（型号YN6-NPT1/4，上海威月仪表仪器有限公司）等；气路系统包括空气压缩机1（型号750-30< 2 530>，浙江盛源空压机制造有限公司）、油水分离器2（型号AFR2 000，广州市亚德客自动化工业有限公司）、气压表3（型号Y40-02，上海阮隆工业自动化电器有限公司）、减压阀5（型号AR2 000-02，上海阮隆工业自动化电器有限公司）等。雾滴粒径测试设备为激光粒度分析仪7（型号Winner318B，济南微钠颗粒颗粒仪器有限公司，量程15-711m，分30级）。雾滴粒径谱测试系统示意图如图8c所示。

试验方案安排如下：分别在不同的进气压力（0.05、0.06、0.07、0.08、0.09、0.1、0.11、0.12、0.13、0.14、0.15、0.2、0.3、0.4、0.5 MPa）下及取不同值（3.5、4.5、5.5、6.5、7.5、8.5、10、11.5 mm）时测得索太尔平均粒径SMD的变化情况，试验过程中，水流量控制在 2 L/h。

4.2 试验结果与分析

4.2.1 3种结构型式喷嘴在不同供气压力下雾滴粒径的变化情况

试验结果如图9a所示，在试验过程中，当供气压力从0 MPa逐渐增大的过程中，只有当压力达到一定的值才会有大量较小雾滴，称之为“雾化起始点”，图9a可以看出3种腔体的“雾化起始点”分别为：0.11、0.08、0.07 MPa。在“雾化起始点”3种喷头的SMD基本一致，约为57m。由SMD变化趋势可以看出，当in由“雾化起始点”增大至0.5 MPa的过程中，阶梯腔式喷头的雾滴粒径由56.469m减小到42.837m，而圆柱腔式喷头的SMD由57.079m减小到48.550m。带有阶梯腔的Hartmann雾化喷头比带有圆柱腔的喷头粒径小，且在压力较小（低于0.15 MPa）时，两种喷头的雾滴粒径差较小，差距约为3.5m，而压力较高时粒径差明显变大差距约为 6m，SMD变化曲线会出现一个明显的转折点。

4.2.2 Laval管出口与谐振腔之间的距离对雾滴粒径的影响

试验结果如图9b所示，对于无圆锥罩的阶梯腔式超声雾化喷嘴，当Laval管出口与谐振腔之间的距离由3.5 mm增大至11.5 mm的过程中，SMD呈现先变小后变大的趋势，在=6.5 mm处雾滴粒径达到最小值，in为0.4 、0.3、0.2 MPa时SMD最小值分别为44.847、43.164、41.902m。由图10可以看出当在5.5~7.5 mm范围内时，雾滴粒径受的影响不大，对于供气压力为0.3 MPa的情况，在这个范围内SMD约为42m，而在<5.5 mm 和>8.5 mm的范围内，雾滴粒径随着的变大分别呈现出明显变小和急剧上升的趋势，当in=0.3 MPa时，随着由3.5 mm增大到9.5mm，SMD先由51.827m减小到 43.164m，后又增大到53.865m。随着的持续增大，谐振腔谐振现象渐渐消失，之后雾滴粒径主要受供气压力的影响，如图11所示，在供气压力恒定时，雾滴粒径随着的变大而变大，在>10.5 mm时变化幅度趋于平缓，以in=0.3 MPa时为例，此时SMD约为58m。

为观察¢点最大静压力max、拉瓦尔管出口与谐振腔之间的距离和SMD的变化关系，将三者关系以三维视图的形式呈现在图10中。综合图9、图10及表2可知雾滴SMD与腔内流体压力、声压级以及谐振腔谐振状态等因素密切相关，而腔内流体发生稳定回流震荡时，其声压级显著增大，这对雾滴的进一步细化起决定性作用。

4.2.3 阶梯腔深度比2/1对雾滴粒径的影响

根据上节试验结果，取试验结果较优的值为 6.5 mm，在供气压力in分别为0.2 MPa、0.3 MPa、0.4 MPa时，测定当21变化时，雾滴粒径的变化情况。试验结果如图12所示，结果表明，当2/1由0增大至5的过程中，雾滴粒径呈现出先急剧变小后缓慢增大的过程。而极小值点出现在21取值为1附近时，也就是说，当阶梯腔第二级阶梯孔的深度2由0变大时，在一定的范围内（2<1.51）对于雾滴粒径有着明显的改善作用。以in=0.3 MPa时为例，最小SMD可达到43m左右。综合图12和表1可以看出，雾滴粒径和谐振腔的谐振频率有一定相关性，谐振频率的增大使雾滴粒呈现出变小的趋势。

综上分析，较优的阶梯型谐振腔深度比21范围为0.5～1.5，可将此结构参数范围作为常用的阶梯腔工作范围。

a. 带谐振腔的Hartmann低频超声雾化喷嘴雾滴粒径测试现场

a. Droplet size distribution test spot of Hartmann atomization nozzle with resonance tube

b. 喷嘴整体图及其阶梯腔装置

b. Whole body of the nozzle and its stepped tube device

c. 雾滴粒径谱测试系统示意图

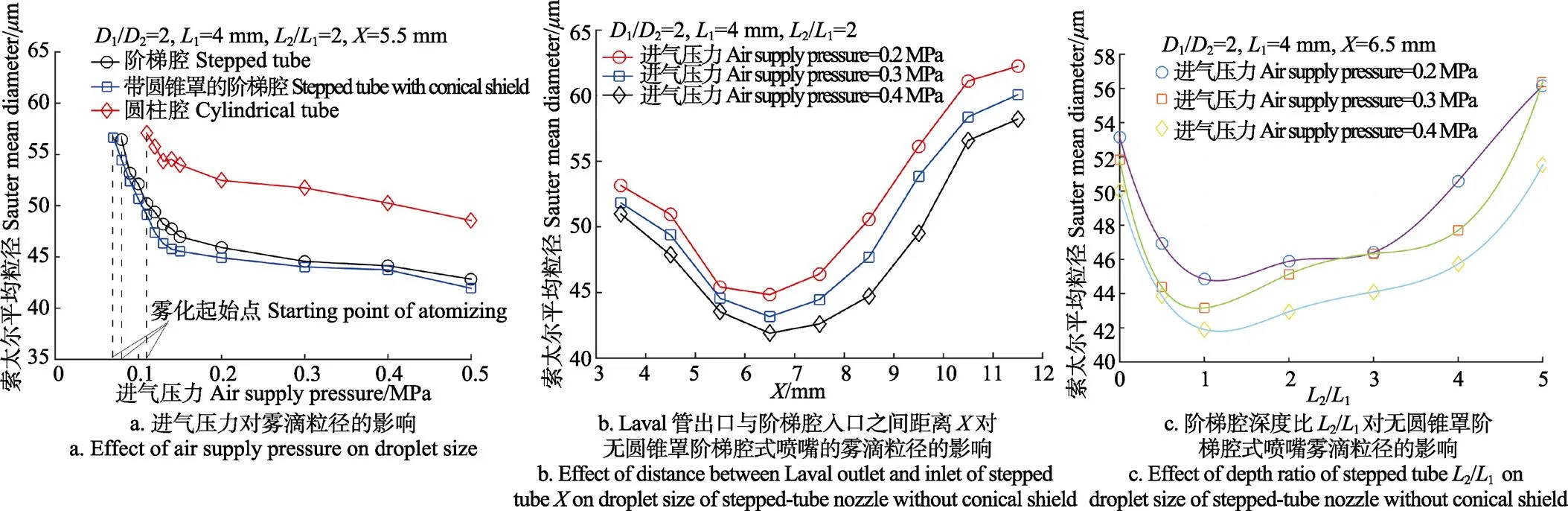
图9 3种腔体喷嘴在不同进气压力下喷嘴雾滴粒径对比

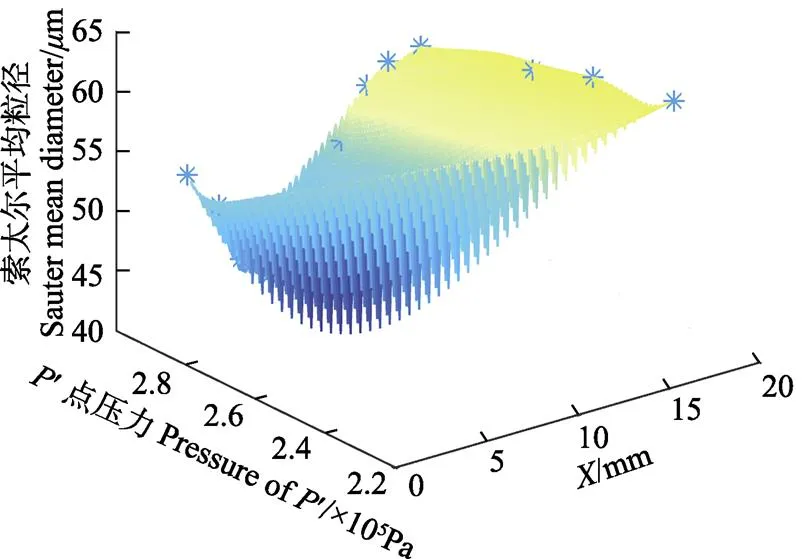
图10 SMD在P¢点压力及拉瓦尔管出口与谐振腔之间的距离X作用下的变化情况

Fig.11 Effect of pressure of¢and distance between Laval outlet and inlet of stepped tubeon SMD

5 结 论

通过对圆柱腔、阶梯腔、带有圆锥罩的阶梯腔的3种雾化喷头进行数值模拟，参数化研究了第二级阶梯孔与第一级阶梯孔深度比、圆锥罩、第二级阶梯孔与第一级阶梯孔孔径比、以及Laval管出口与谐振腔之间的距离对谐振状态及谐振频率的影响；最终选取较优的孔径比为2，对喷嘴进行试制，对3种雾化喷头进行了雾滴粒径对比测试，并进行了雾滴粒径谱的参数化对比测试试验，雾化量为2 L/h下，试验测得阶梯腔式超声雾化喷嘴的最小雾滴粒径为42m。

并得出如下结论：

1）在相同参数条件下，第二级阶梯孔与第一级阶梯孔深度比超过2时其谐振频率即达到了传统圆柱型谐振腔谐振频率的1.6至1.7倍。

2）在Laval管出口和谐振腔入口之间的圆锥罩使得腔内气体压力波动幅度变大。圆锥罩与阶梯腔出口之间的涡流形成与消失的过程中，对腔内气体的入流和出流造成周期性的扰动。

3）第二级阶梯孔与第一级阶梯孔孔径比对谐振腔的谐振状态有较大影响，其改变会使阶梯型谐振腔的谐振模式由“回流模式”转变为“尖声模式”或使谐振现象消失，孔径比的较优范围为1.2～2。

4）带有阶梯腔的雾化喷嘴比带有圆柱腔的雾化喷嘴雾滴粒径小2～6m，且在压力较小（低于0.15 MPa）时其差距较小，而压力较高时粒径差明显变大。圆锥罩使得低压时的雾滴粒径随供气压力变化更加敏感。

5）Laval管出口与谐振腔之间的距离也是影响雾滴粒径的重要因素，对于带阶梯腔的喷头，当该距离为 6.5 mm时索太尔平均粒径SMD达到最小值，SMD的变化趋势与腔内声压级的变化趋势基本一致。且在粒径最小值附近，谐振腔处于谐振最佳状态。

6）较优的阶梯型谐振腔第二级阶梯孔与第一级阶梯孔深度比范围为0.5～1.5，可将此结构参数范围作为常用的阶梯腔工作范围。

[1] Hartmann J, Trolle B. A new acoustic generator. The air- jet-generator[J]. Journal of Scientific Instruments, 1927, 4(4): 101－111.

[2] Raman G, Khanafseh S, Cain A B, et al. Development of high bandwidth powered resonance tube actuators with feedback control[J]. Journal of Sound & Vibration, 2004, 269(3): 1031－1062.

[3] Raman G, Srinivasan K. The powered resonance tube: From Hartmann’s discovery to current active flow control applications[J]. Progress in Aerospace Sciences, 2009, 45(4/5): 97－123.

[4] Sreejith G J, Narayanan S, Jothi T J S, et al. Studies on conical and cylindrical resonators[J]. Applied Acoustics, 2008, 69(12): 1161－1175.

[5] Iii RFM, Pavlak A. Tapered resonance tubes-Some experiments[J]. Aiaa Journal, 2015, 8(3): 571－572.

[6] Murugappan S, Gutmark E. Parametric study of the Hartmann- Sprenger tube[J]. Experiments in Fluids, 2005, 38(6): 813－823.

[7] Antao D S, Farouk B. High amplitude nonlinear acoustic wave driven flow fields in cylindrical and conical resonators[J]. Journal of the Acoustical Society of America, 2013, 134(2): 917－932.

[8] Cain A, Kerschen E, Raman G, et al. Simulation of Powered Resonance Tubes: Understanding Parameter Space[C]// Aiaaceas Aeroacoustics Conference and Exhibit, 2003.

[9] Jack Wilson, Mark P Wernet, Daniel E Paxson. Vortex rings generated by a shrouded hartmann-sprenger tube[J]. Aiaa Journal, 2015, 44(11): 2706－2718.

[10] Sarohia V, Back L H. Experimental investigation of flow and heating in a resonance tube[J]. Journal of Fluid Mechanics, 1979, 94(10): 649.

[11] Masaaki Kawahashi，Makato Suzuki. Wave motions and thermal effects in stepped hs tubes (1st report, experimental results and numerical analyisis for tubes with one step)[J]. Transactions of the Japan Society of Mechanical Engineers B, 1983, 49(437): 121－129.

[12] Raman G, Mills A, Kibens V. Development of powered resonance-tube actuators for aircraft flow control applications[J]. Journal of Aircraft, 2015, 41(6): 1306－1314.

[13] 夏允庆，程华定. 杆式声雾化器雾化特性的试验研究[J]. 航空动力学报，1995，10(1)：93－95.

[14] 张绍坤，王景甫，马重芳. 流体动力式超声波喷嘴雾化特性的实验研究[J]. 石油机械，2007，35(6)：1－3.

[15] Raman G, Srinivasan K. The powered resonance tube: From Hartmann’s discovery to current active flow control applications[J]. Progress in Aerospace Sciences, 2009, 45(4/5): 97－123.

[16] Narayanan S. Atomization in the acoustic field of a Hartmann whistle[J]. International Journal of Spray & Combustion Dynamics, 2013, 5(1): 1－24.

[17] Marchese V P, Rakowsky E L, Bement L J. A Fluidic sounding rocket motor ignition system[J]. Journal of Spacecraft & Rockets, 1973: 10: 731－734.

[18] Xia G, Li D, Merkle C L. Effects of a needle on shrouded Hartmann-Sprenger tube flows[J]. Aiaa Journal, 2015, 45(45): 1028－1035.

[19] 阮灿，黄玥，蔡江千. 基于Hartmann谐振腔的雾化喷嘴声 场流场特性[J]. 航空动力学报，2016，31(9)：2104－2114. Ruan Can, Huang Yue, Cai Jiangqian. Aeroacoustic and flow field features of ultrasonic atomizer based on Hartmann resonance tube[J]. Journal of Aerospace Power, 2016, 31(9): 2104－2114. (in Chinese with English abstract)

[20] Li Bo，Hu Guohui，Zhou Zhewei. Numerical simulation of flow in Hartmann resonance tube and flow in ultrasonic gas atomizer[J]. Applied Mathematics & Mechanics, 2007, 28(11): 1415－1426.

[21] 祖洪彪，周哲玮，王志亮. 双激励超音速气体雾化喷嘴共振特性的数值研究[J]. 应用数学和力学，2012，33(12)： 1379–1391.Zu Hongbiao, Zhou Zhewei, Wang Zhiliang. Properties of acoustic resonance in a double actuator ultrasonic gas nozzle: A numerical study[J]. Applied Mathematics and Mechanics, 2012, 33(12): 1379－1391. (in Chinese with English abstract)

[22] Bulovich S V. Numerical investigation of the laminar shock-wave gas flow excited by harmonic vibrations of the piston in a closed cylindrical tube[J]. Journal of Engineering Physics and Thermophysics, 2006, 79(2): 354－359.

[23] Tian Zhangfu，Gong Changchao，Kong Xiaopeng. The experiment and simulation study of the powered resonance tube driven by annular jet[J]. Applied Mechanics & Materials, 2014, 602－605: 3013－3016.

[24] Kuno Foelsch. The analytical design of an axially symmetric Laval nozzle for a parallel and uniform jet[J]. International Journal of Orthodontics, 2015, 20(3): 39－40.

[25] Danilov S D, Mironov M A. Breakup of a droplet in a high-intensity sound field[J]. Journal of the Acoustical Society of America, 1992, 92(5): 2747—2755.

[26] Sivadas V, Fernandes E C, Heitor M V. Acoustically excited air-assisted liquid sheets[J]. Experiments in Fluids, 2003, 34(6): 736－743.

[27] Raman Sujith. An experimental investigation of interaction of sprays with acoustic fields using PIV[J]. Experiments in Fluids, 2005, 38(5): 576－587.

[28] Thompson P A. Jet-driven resonance tube[J]. Aiaa Journal, 2015, 2(7): 1230－1233.

[29] 郭烈锦. 两相与多相流动力学[M]. 西安：西安交通大学出版社，2002.

[30] Brocher E, Duport E. Resonance tubes in a subsonic flowfield[J]. Aiaa Journal, 2015, 26(5): 548－552.

Design and test of low-frequency Hartmann atomization nozzle with stepped resonance tube

Gao Jianmin, Ma Junlong

(212013,)

The droplet quality of hydrodynamic ultrasonic atomization nozzle is better than the ordinary two-phase nozzle. And the atomization amount is larger than the piezoelectric atomization nozzle. High-quality droplet and high atomization amount are both required in the field of aeroponics. Therefore, it is necessary to develop a hydrodynamic ultrasonic atomizing nozzle suitable for large-scale aeroponics. Based on the basic principle of the Hartmann resonator, in this study, the mechanism of ultrasonic vibration of resonant cavity and the atomization mechanism of resonant cavity supersonic nozzle were analyzed theoretically. The Hartmann low-frequency ultrasonic atomization nozzle with stepped resonator and adjustable structural parameters was designed, including the Laval tube, the stepped tube, and conical shield. The influence of the structural parameters on the resonant state of the resonator was studied by means of CFD software transient numerical simulation. In order to make the spraying angle controllable, active flow control was used in the atomizing area, namely, adding a conical shield at the exit of the nozzle. The oscillation characteristics of the stepped resonance tube were further studied parametrically by numerical simulation methods. Numerical simulation of three kinds of atomizing nozzles including cylindrical tube, stepped tube and stepped tube with conical shield was carried out. The parameters which were studied were as follows: the distance between Laval outlet and inlet of stepped tube, depth ratio of the second stepped hole and the first stepped hole, conical cover, diameter ratio of the second stepped hole and the first stepped hole. Numerical simulation results showed that: (1) If the depth ratio of the stepped tube exceeded 2, its resonance frequency reached 1.6 to 1.7 times of the cylindrical one under the same working parameters; (2) The conical shield can make the pressure oscillation amplitude in the cavity bigger; and (3) The diameter ratio of the stepped resonator had a great influence on the resonant state of the resonator. The variation of diameter ratio of the stepped resonator changed the resonant mode of the stepped resonator from one mode to another. It also can make the resonance phenomenon disappear. As such, the key dimensions of the stepped resonator were determined accordingly. And an optimal diameter ratio was selected for trial production. And the optimal distance between Laval tube outlet and the resonant inlet 5.5 mm were selected as the initial structural parameter values of the spray test. The droplet size of three kinds of atomizing nozzles was tested and the test of droplet size was carried out with distance between Laval tube outlet and the resonant inlet, depth ratio of the second stepped hole and the first stepped hole, and other factors as variables. Moreover, its atomization properties were tested contrastively under different conditions. Research results showed that: (1) Start-up properties of oscillation can be optimized due to the main frequency unaffected by the conical shield；(2) The diameter ratio of stepped resonance tube was a quite sensitive parameter influencing the resonance state. The variation of diameter ratio can make the resonance mode change from ‘jet regurgitant mode’ to ‘jet scream mode’ or make the oscillation disappear; (3) Atomization properties of Hartmann atomization nozzle with a stepped resonance tube was better than those of Hartmann atomization nozzle with a cylindrical one; (4) If the air supply pressure was low, the droplet size was more sensitive with the pressure after adding a conical shield, while the gap of the average droplet size between the nozzle with stepped tube and that with traditional tube was not obvious under the condition of high air supply pressure. The distance between the Laval tube exit and the resonance tube was another sensitive parameter influencing the droplet size. An optimal distance, where the minimum droplet size can be acquired, was 6.5 mm. The droplet diameter increased gradually no matter the distance was bigger or smaller than the optimal distance. However, the droplet diameter varied slightly with the distance near the optimal point.

nozzles; numerical simulation; spraying; test; Hartmann low-frequency ultrasonic nebulization; stepped resonance tube; conical shield

10.11975/j.issn.1002-6819.2017.12.009

S224.3

A

1002-6819(2017)-12-0066-08

2016-10-12

2017-06-05

国家自然科学基金资助项目（51275214）；江苏自然科学基金资助项目（BK2011470）；江苏高校优势学科建设工程资助项目（苏财教（2011）8号）

高建民，男，江西吉水人，研究员，博士，主要从事超声精密喷雾技术研究，2010-2011年由教育部公派赴美国农业部研究院农业工程应用技术地面喷雾国家实验室研修（USDA/ARS）。镇江江苏大学现代农业装备与技术教育部重点实验室，212013。Email：1000001903@ujs.edu.cn

高建民，马俊龙.带阶梯型谐振腔的Hartmann低频超声雾化喷嘴设计及试验[J]. 农业工程学报，2017，33(12)：66－73. doi：10.11975/j.issn.1002-6819.2017.12.009 http://www.tcsae.org

Gao Jianmin, Ma Junlong.Design and test of low-frequency Hartmann atomization nozzle with stepped resonance tube[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2017, 33(12): 66－73. (in Chinese with English abstract) doi：10.11975/j.issn.1002-6819.2017.12.009 http://www.tcsae.org