基于干扰观测器的欠驱动AUV自适应反演控制

陈巍，魏延辉，曾建辉，胡佳兴，王泽鹏



基于干扰观测器的欠驱动AUV自适应反演控制

陈巍，魏延辉，曾建辉，胡佳兴，王泽鹏

(哈尔滨工程大学自动化学院，黑龙江哈尔滨，150001)

针对未知外界干扰存在的情况，提出一种基于非线性干扰观测器(NDO)的自适应反演控制，用于改善欠驱动自治水下机器人(AUV)深度跟踪控制性能。首先对欠驱动自治水下机器人的垂直面模型进行有条件的简化，得到新的运动学及动力学方程，建立简化后模型的状态方程；其次根据系统状态方程构建非线性观测器，设计自适应反演控制器，输出控制量根据李雅普诺夫稳定原理推导得出，确保包含非线性干扰观测器及自适应反演控制器在内的控制系统的一致渐进稳定性。研究结果表明：所设计的非线性干扰观测器以及自适应反演控制器可以实现欠驱动自治水下机器人在存在外界未知干扰情况下深度轨迹跟踪，具有较强的鲁棒性。

欠驱动自治水下机器人；深度跟踪；非线性干扰观测器；自适应；反演法

自治水下机器人(AUV)是一种能够进行自主运行，不需要实时干预过程的水下智能机器人，相对于遥控水下机器人而言，AUV具有作业范围约束少，作业过程中可深可浅，可单个作业，亦可多个协同工作等特点[1−2]。由于其独特的优势，AUV被广泛用于深海的各种作业活动，诸如海底矿物勘测，海图绘制，军事侦察等。水下机器人由于需要完成各式各样的任务，故对于其姿态控制以及运动控制的设计十分重要。欠驱动AUV是AUV中一种常见的类型，其特点是控制输入的数目小于运动所涉及自由度的数目。目前针对欠驱动AUV控制的研究主要包括水平面，垂直面，以及三维轨迹跟踪等研究方向[3−6]，贾鹤鸣等[6]基于自适应反步法设计实现了欠驱动AUV对时变航迹进行跟随控制的目标。ZHANG等[7]构建了一种新型的自适应控制器，该方法基于 DRFNN实现在线预测动态特性未知的非线性路径。RAIMONDI等[8]建立了一个多闭环模糊控制器用来实现欠驱动AUV水平面内横向运动的控制。高剑等[9]基于级联系统理论，独立设计了位置以及航向角2个独立的跟踪控制器，研究了欠驱动AUV水平面轨迹跟踪问题。万磊等[10]针对模型不确定情况下的欠驱动AUV水平面内轨迹跟随问题，设计了可以有效避免系统抖振现象的自适应模糊滑模控制器。LI等[11]将AUV的垂直面内动力学模型简化为严格的非线性反馈系统，从而实现垂直面内运动的控制。NAIK等[12]将欠驱动AUV深度控制的限制问题等转换为依据SDRE方法设计一个增广系统控制器，实现了问题的转化。陈子印等[13]通过自适应控制器对神经网络控制器误差进行消除，提出了针对AUV反馈增益的变深控制方法。周佳加等[14]对于无人水下航行器UUV的水平面路径跟踪，提出了一种自适应神经控制方法。非线性干扰观测器(NDO)大多数用于非线性系统以及存在未知外界干扰的情况下，对所控制系统的各类不确定项进行补偿，从而改善系统对于不确定外界干扰的承受能力[15−16]。乔继红等[15, 17]基于NDO的思想，分别观测直升机系统和高超声速飞行器系统包括外干扰在内的不确定项，提高了系统跟踪期望轨迹的性能；自适应反演控制方法由自适应算法和反演控制相结合得到，可以消除被控系统时变参数以及未知外界干扰对系统的影响，具有广泛的应用领域，张利军等[3, 6, 17]分别在AUV深度、AUV三维航迹跟踪以及飞行器的滑模控制等控制器设计过程中引入自适应反演算法，提升了系统的动态性能。近年来，针对欠驱动AUV受到外界干扰的控制研究大多集中在系统本身参数自适应规律的设计上，在此基础上引入智能控制、鲁棒控制、增益调节等，设计过程较为复杂，却相对较少关注干扰本身的预测和估计。基于NDO的自适应反演控制算法，可以实现外界干扰的观测以及控制输入的补偿，降低控制器的设计难度。本文作者采用基于非线性干扰观测器的自适应控制方法来解决在不确定外干扰条件下，依靠舵角控制，实现欠驱动自治水下机器人跟踪期望深度。根据李雅普诺夫稳定性理论，在确保系统一致渐近稳定的前提下，设计与构建了非线性干扰观测器和自适应控制器，确定了舵角控制的表达式和自适应规律。最后仿真实验的结果可以验证该控制方法在满足欠驱动AUV垂直面简化模型的相关条件下，能很好地实现控制目标，表现出较强的抵抗外界未知干扰的鲁棒性。

1 欠驱动AUV垂直面模型

对于AUV而言，通常采用牛顿−欧拉方法建立其六自由度的运动学及动力学模型[6]，其矩阵表示形式如下：

为得到欠驱动AUV垂直面运动学以及动力学模型，假设AUV水平面与垂直面运动实现解耦，且满足，，，忽略横摇运动对于纵摇以及垂荡运动的干扰，可以得到如下简化的垂直面模型[12]，这里假设由主推进器保证纵向线速度维持在常值，并且满足＞0，欠驱动AUV完成深度跟踪主要依靠舵角作为控制输入。

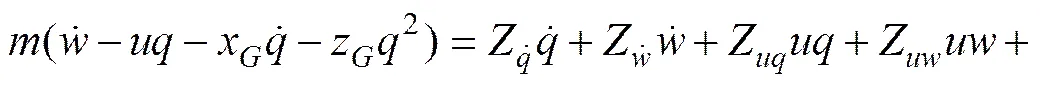
(2)

(3)

(4)

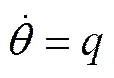
其中：为垂荡速度；为纵倾角速度；为纵倾角；为AUV下潜深度；为纵向速度，假设其维持在常值；为AUV质量；为AUV重力；B为AUV所受浮力；I为绕轴转动惯量；M和Z为舵角系数，和分别为水动力参数和黏滞参数；为舵角控制输入；ext为作用在AUV上的干扰力矩；G和G分别为AUV重心在体坐标系内的坐标分量；B和B分别为AUV浮心在体坐标系内的坐标分量。

因研究需要，对上述模型进一步简化，假设AUV的垂荡速度满足，，纵倾角处于比较小的范围内变化，基本满足，，，，忽略二阶及其以上小项，根据式(3)~(5)得到新的垂直面运动模型[18]：

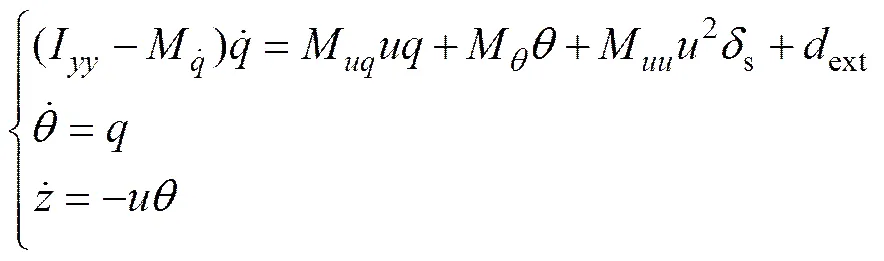
2 基于非线性干扰观测器的自适应反演设计

为了使得依靠舵角控制实现跟踪目标深度，在存在未知外界干扰的情况下，单纯的自适应反演控制器已经无法满足在相对小的控制量前提下实现控制目标。通过引入非线性观测器的设计，可以得到来自于其的补偿输入，弥补了自适应控制器应对突变未知干扰的不足。整个控制系统的设计思路如图1所示。

2.1 非线性干扰观测器的设计

参考非线性观测器的设计方法[19−20]，为方便NDO的设计，定义状态变量，则状态方程可以写成向量形式的表达式。

考虑到非线性干扰观测器的形式，

图1 基于NDO的自适应反演控制系统结构

进一步可知

(11)

定义观测器输出控制量为

2.2 自适应反步法控制器设计

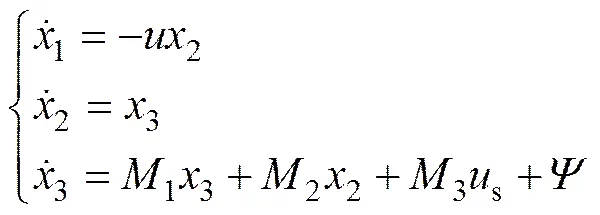
由于对于外干扰的无法预知性，为保证系统的最佳控制性能，需要对观测器得到的干扰误差量进行估计，假设其估计值为，则估计误差量，同样假设观测器得到的干扰误差量相对于控制系统的动态性变化缓慢，即满足，则有，进而设计和引入自适应控制。

根据状态方程，利用反演法设计控制器定义误差变量以及虚拟输入。

(15)

定义控制器第1个虚拟控制量：

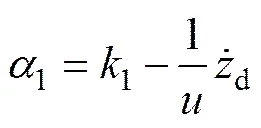
定义纵倾角的跟踪误差量以及Lyapunov函数

(17)

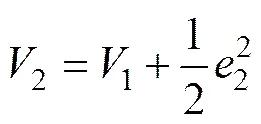
定义控制器第2个虚拟控制量：

k＞0 (19)

定义纵倾角角速度的跟踪误差量以及Lyapunov函数：

(21)

对式(14)，(17)和(20)求导可得

(23)

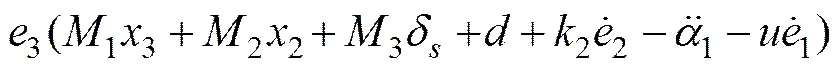
，＞0 (25)

对4求导，得到：

(26)

选取自适应控制律为

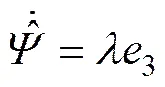
选取自适应反演控制器输出控制量为：

则结合式(26)可知

(29)

综上可以得到AUV的舵角控制规律为

3 仿真实验

某型欠驱动AUV仿真所需相关参数如表1所示，选取设计非线性干扰观测器的参数为：1=1，2=1，3=9 ；自适应反演控制器的参数如下：1=1，2=1.5，3=1，。

表1 AUV仿真参数表

设置AUV的初始深度为5.8 m，其后控制规律控制AUV使其跟踪目标深度，在其运动过程中，对于AUV施加外力矩干扰，设计的AUV目标深度d以及外力矩干扰ext表达式如下:

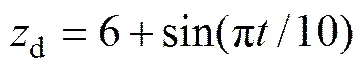
(32)

在AUV跟踪目标深度过程中，舵角控制量由控制器输出控制量以及观测器输出控制量2部分组成。在80≤＜120 s和140≤＜200 s分别对AUV施加突变外力矩干扰和时变外力矩干扰，如图2和图3所示，包含有观测器控制输出量的AUV在受到外界干扰时，几乎完全实现目标深度跟踪；而无观测器控制输出时，如图4和图5所示，AUV深度跟踪在受到干扰时，无法实现完全跟踪目标深度，会出现较大幅度的跟踪误差，最大误差达到0.2 m，相当于变化期望深度幅值 1 m的20%。由图3与图5对比后可见引入非线性干扰观测器对于抵抗外界干扰是十分有效的。

在引入非线性干扰观测器的系统中，干扰力矩实际值及观测值如图6所示。由图6可知：外加干扰力矩的实际值与观测器得到的观测值相差不大，观测器起到了良好的控制补偿作用，并对于干扰力矩实际值与观测值的误差量，引入自适应控制规律得到其估计值，如图7所示。由图7可知：设计的自适应控制律实现了误差的估计，提高了系统的控制精度。

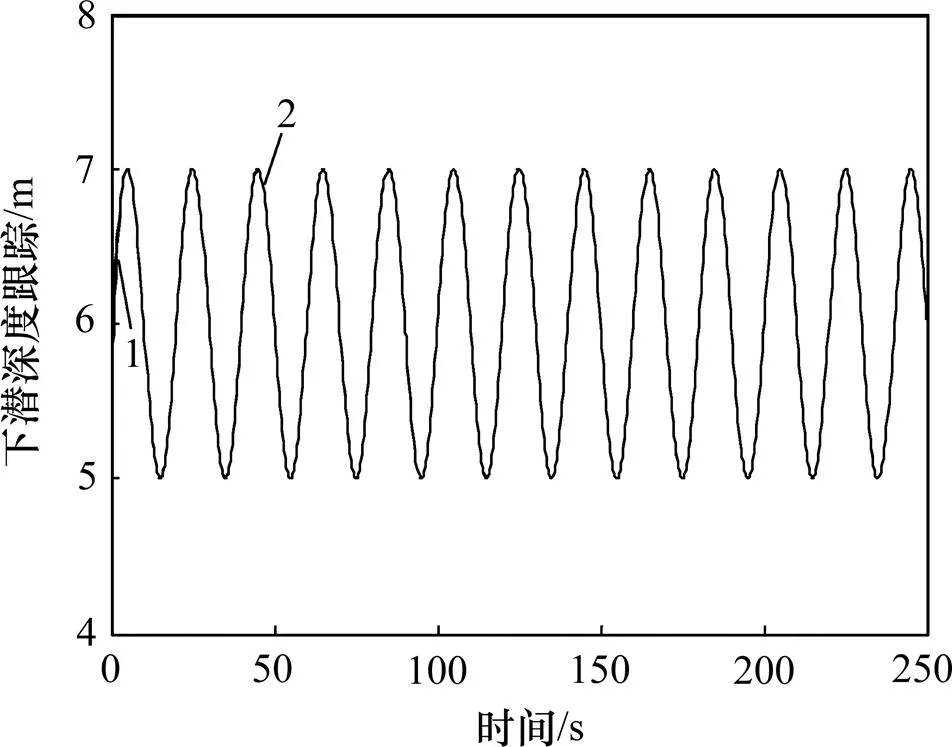
1—AUV目标深度；2—AUV实际深度。

图3 有观测器时AUV深度跟踪误差

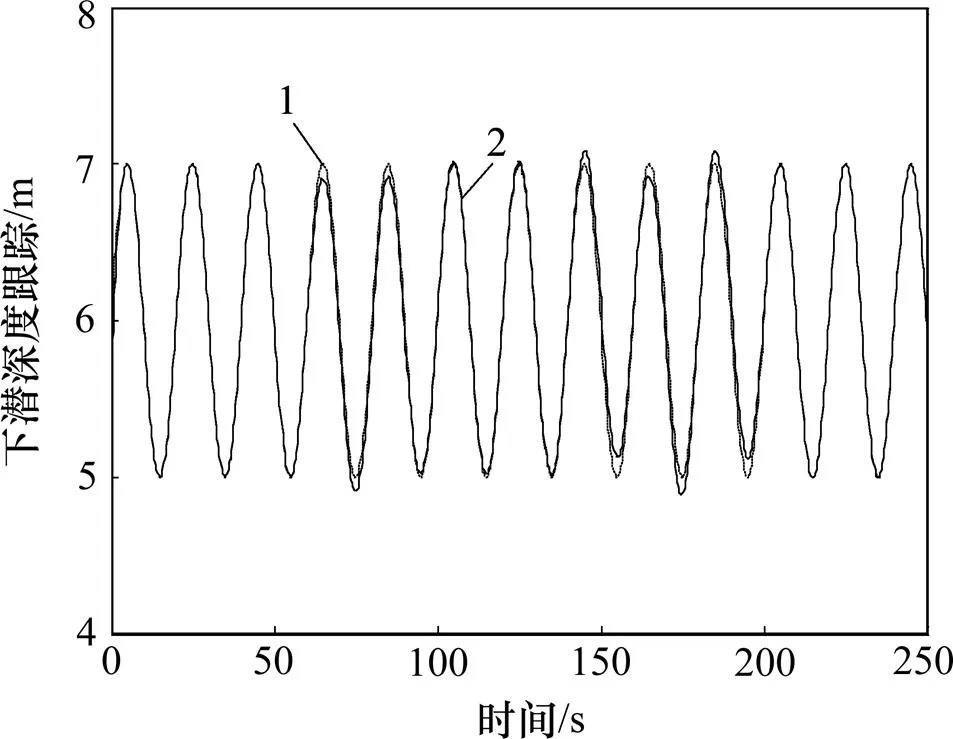
1—AUV目标深度；2—AUV实际深度。

图5 无观测器时AUV深度跟踪误差

1—干扰实际值d；2—干扰观测值。

1—误差实际值；2—误差估计值。

为了验证所设计控制算法的有效性，在突变干扰以及连续干扰时，使用基本PID控制方法进行仿真，对应结果如图10所示。对比所设计的基于NDO的自适应反演控制仿真结果，可以得出所设计控制算法鲁棒性强，控制精度高，跟踪误差小。

基于NDO 自适应反演算法控制AUV跟踪目标深度的过程中，可以得到其各个状态变量的变化曲线，如图11所示。由图11可以看出：在平稳跟踪过程中，纵倾角最大值只有10°左右，垂荡速度m/s，满足模型简化的条件。综上，可以得出该基于非线性 干扰观测器的自适应反演控制取得了较好的控制效果。

1—ud；2—us。

图9 舵角控制量

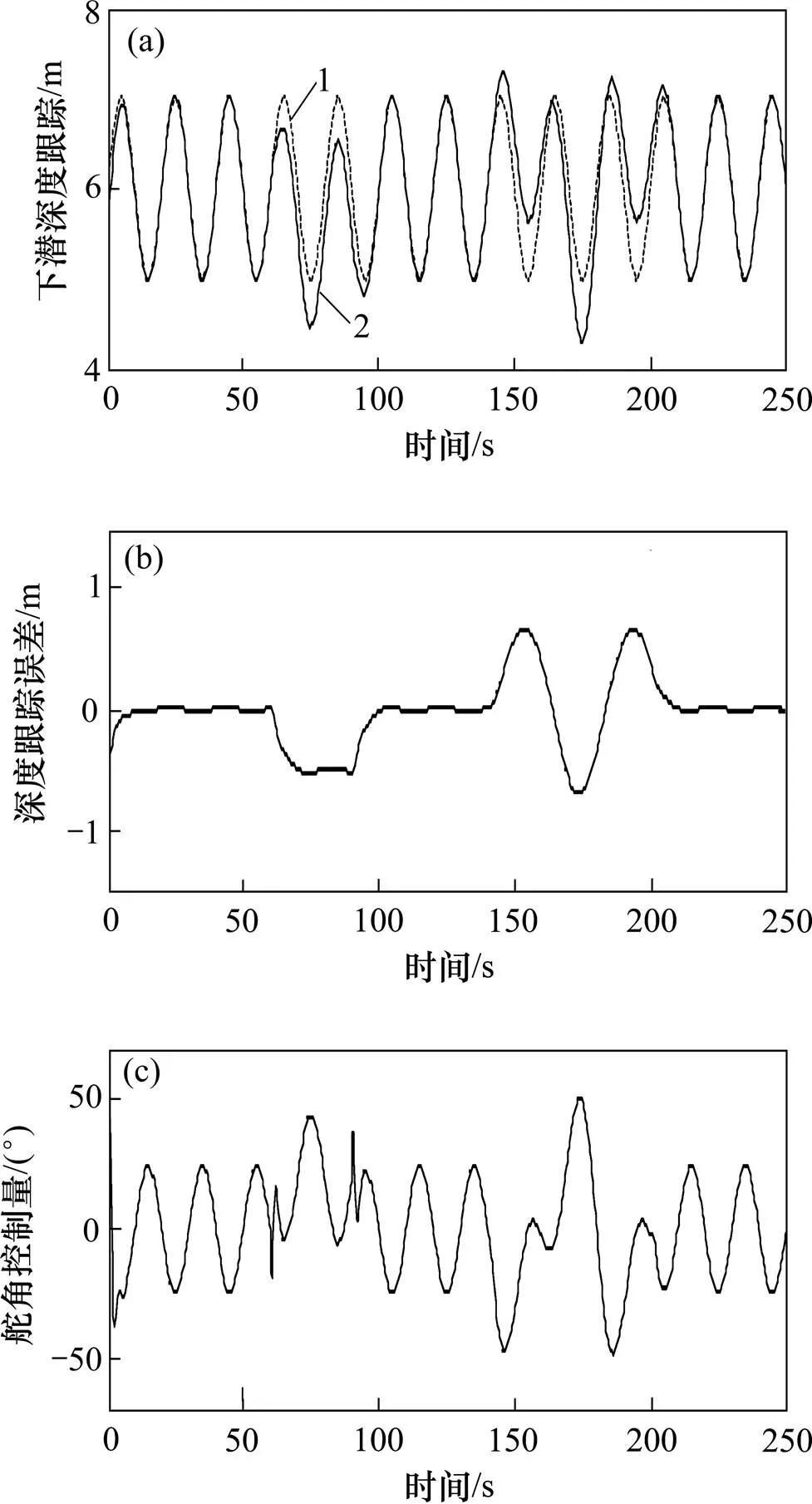
(a) AUV深度跟踪；(b) 深度跟踪误差；(c) PID舵角控制

(a) θ; (b) q; (c) w

4 结论

1) 通过对欠驱动AUV的垂直面内运动学以及动力学方程提出简化条件进行简化，得到简化的欠驱动模型。

2) 针对AUV受到外界干扰情况，引入非线性干扰观测器，并对于观测器观测的外界干扰误差引入自适应控制规律，在此基础上，设计了自适应反演控制器。

3) 通过给定具体的AUV仿真参数进行仿真实验，得到在外界干扰作用下，干扰观测值、控制器输出控制量、观测器输出控制量和舵角控制量等一系列变量曲线，基于其变化规律的分析，验证了所设计控制方法良好的控制性能。

[1] 封锡盛, 李一平, 徐红丽. 下一代海洋机器人: 写在人类创造下潜深度世界记录10 912 m 50周年之际[J]. 机器人, 2011, 33(1): 113−118. FENG Xisheng, LI Yiping, XU Hongli. The next generation of unmanned marine vehicles dedicated to the 50 anniversary of the human world record diving 10 912 m[J]. Robot, 2011, 33(1): 113−118.

[2] 徐玉如, 肖坤. 智能海洋机器人技术进展[J]. 自动化学报, 2007, 33(5): 518−521. XU Yuru, XIAO Kun. Technology development of autonomous ocean vehicle[J]. Acta Automatica Sinica, 2007, 33(5): 518−521.

[3] 张利军, 齐雪, 赵杰梅, 等. 垂直面欠驱动自治水下机器人定深问题的自适应输出反馈控制[J]. 控制理论与应用, 2012, 29(10): 1371−1376.ZHANG Lijun, QI Xue, ZHAO Jiemei, et al. Depth-keeping control for autonomous underwater vehicle in vertical plane using adaptive output feedback controller[J]. Control Theory & Applications, 2012, 29(10): 1371−1376.

[4] 俞建成, 张艾群, 王晓辉, 等. 基于模糊神经网络水下机器人直接自适应控制[J]. 自动化学报, 2007, 33(8): 840−846. YU Jiancheng, ZHANG Aiqun, WANG Xiaohui, et al, Direct adaptive control of underwater vehicles based on fuzzy neural networks[J]. Acta Automatica Sinica, 2007, 33(8): 840−846.

[5] 魏延辉, 彭富国, 盛超, 等. 自主式水下机器人运动稳定性控制方法[J]. 华中科技大学学报(自然科学版), 2014, 42(2): 127−132. WEI Yanhui, PENG Fuguo, SHENG Chao, et al. Control method of the stability of AUV[J]. Journal of Huazhong University of Science and Technology (Natural Science Edition), 2014, 42(2): 127−132.

[6] 贾鹤鸣, 程相勤, 张利军, 等. 基于自适应Backstepping的欠驱动AUV三维轨迹跟踪控制[J]. 控制与决策, 2012, 27(5): 652−657. JIA Heming, CHENG Xiangqin, ZHANG Lijun, et al. Three-dimensional path tracking control for underactuated AUV based on adaptive backstepping[J]. Control and Decision, 2012, 27(5): 652−657.

[7] ZHANG Lijun, QI Xue, PANG Yongjie. Adaptive output feedback control based on DRFNN for AUV[J]. Ocean Engineering, 2009, 36: 716−722.

[8] RAIMONDI F M, MELLUSO M. Hierarchical fuzzy/Lyapunov control for horizontal plane trajectory tracking of under- actuated AUV[C]// Proceeding of 2010 IEEE International Symposium on Industrial Electronics. Bari, Italy: IEEE, 2010: 1875−1882.

[9] 高剑, 徐德民, 严卫生, 等. 欠驱动自主水下航行器轨迹跟踪控制[J]. 西北工业大学学报, 2010, 28(3): 404−408. GAO Jian, XU Demin, YAN Weisheng, et al. Applying cascaded systems theory to ensuring globally uniformly asymptotical stability of trajectory tracking controller of underactuated autonomous underwater vehicle(AUV)[J]. Journal of Northwestern Polytechnical University, 2010, 28(3): 404−408.

[10] 万磊, 崔士鹏, 张国成, 等. 欠驱动水下机器人航迹跟踪控制[J]. 电机与控制学报, 2013, 17(2): 103−111. WAN Lei, CUI Shipeng, ZHANG Guocheng, et al. Path following control of underactuated autonomous underwater vehicles[J]. Electric Machines and Control, 2013, 17(2): 103−111.

[11] LI J H, LEE P M. Path tracking in dive plane for a class of torpedo-type underactuated AUVs[C]// Proceedings of the 7th Asian Control Conference. Hong Kong, China: IEEE, 2009: 360−365.

[12] NAIK M S, SINGH S N. State-dependent Riccati equation-based robust dive plane control of AUV with control constraints[J]. Ocean Engineering, 2007, 34(11/12): 1711−1723.

[13] 陈子印, 王宏健, 边信黔, 等. 基于反馈增益的AUV稳定神经网络反步变深控制[J]. 控制与决策, 2013, 28(3): 407−412. CHEN Ziyin, WANG Hongjian, BIAN Xinqian, et al. Stable neural network backstepping for diving control of AUV based on feedback gain[J]. Control and Decision, 2013, 28(3): 407−412.

[14] 周佳加, 严浙平, 贾鹤鸣, 等. 改进规则下自适应神经网络的UUV水平面路径跟随控制[J]. 中南大学学报(自然科学版), 2014, 45(9): 3021−3028. ZHOU Jiajia, YAN Zheping, JIA Heming, et al. Improved path-following in horizontal plane for UUV using adaptive neural network controller[J]. Journal of Central South University (Science and Technology), 2014, 45(9): 3021−3028.

[15] 乔继红, 戴亚平, 刘金琨. 基于非线性干扰观测器的直升机滑模反演控制[J]. 北京理工大学学报, 2009, 29(3): 224−228. QIAO Jihong, DAI Yaping, LIU Jinkun. Sliding backstepping control for helicopters with nonlinear disturbance observer[J]. Transactions of Beijing Institute of Technology, 2009, 29(3): 224−228.

[16] 贾鹤鸣, 宋文龙. 基于非线性干扰观测器的L2滤波反步控制[J]. 中南大学学报(自然科学版), 2014, 45(8): 2640−2647. JIA Heming, SONG Wenlong. L2 filtered backstepping control based on nonlinear disturbance observer[J]. Journal of Central South University (Science and Technology), 2014, 45(8): 2640−2647.

[17] 宋超, 赵国荣, 盖俊峰. 基于非线性干扰观测器的高超声速飞行器反演滑模控[J]. 系统工程与电子技术, 2012, 34(6): 1231−1234. SONG Chao, ZHAO Guorong, GAI Junfeng. Sliding mode backstepping control for hypersonic aircraft based on nonlinear disturbance observer[J]. Systems Engineering and Electronics, 2012, 34(6): 1231−1234.

[18] KELLER J J. Tracking control of autonomous underwater vehicles[D]. Monterey, CA: School of Naval Postgraduate. Department of Mechanical Engineering, 2002: 5−7.

[19] MOHAMMED S, HUO W G, HUANG J, et al. Nonlinear disturbance observer based sliding mode control of a human-driven knee joint orthosis[J]. Robotics and Autonomous Systems, 2016, 75: 41−49.

[20] CHEN W H, BALANCE D J, GAWTHROP P J. A nonlinear disturbance observer for robotic manipulators[J]. IEEE Transactions on Industrial Electronics, 2000, 47(4): 932−938.

(编辑 杨幼平)

Adaptive backstepping control of underactuated AUV based on disturbance observer

CHEN Wei, WEI Yanhui, ZENG Jianhui, HU Jiaxing, WANG Zepeng

(College of Automation, Harbin Engineering University, Harbin 150001, China)

In order to improve the depth tracking control performance of underactuated autonomous underwater vehicle (AUV), an adaptive backstepping controller based on nonlinear disturbance observer (NDO) was proposed considering unknown external disturbance. Firstly, the vertical plane motion model of underactuated AUV was simplified according to some limited conditions. The new kinematics and dynamics equations were obtained, and the state equations of simplified model were established as well. Secondly, on the basis of state equations, a nonlinear disturbance observer was constructed. In the meanwhile, an adaptive backstepping controller was designed based on NDO, and then the control output was obtained according to the Lyapunov stability principle, which globally guaranteed the asymptotical stability of the whole control system. The results show that designed NDO and adaptive backstepping controller can effectively achieve depth trajectory tracking of underactuated AUV in the case of unknown external disturbance, and show strong robustness to disturbance.

underactuated AUV; depth tracking; nonlinear disturbance observer; adaptive control; backstepping control

10.11817/j.issn.1672-7207.2017.01.010

TP24

A

1672−7207(2017)01−0069−08

2016−01−04；

2016−03−15

国家自然科学基金资助项目(51205074)；国家科学技术部国际科技合作项目(2014DFR10010)；中央高校基本科研业务费专项资金资助项目(HEUCF041703)；高等学校博士学科点专项科研基金资助项目(20112304120007) (Project(51205074) supported by the National Natural Science Foundation of China; Project(2014DFR10010) supported by the Ministry of Science and Technology of China; Project(HEUCF041703) supported by the Fundamental Research Funds for the Central Universities; Project(20112304120007) supported by the Research Fund for the Doctoral Program of Higher Education of China)

魏延辉，博士，硕士生导师，从事机器人控制、可重构机器人以及水下机器人等研究；E-mail: wyhhit@163.com