考虑打桩反弹的组合锤头冲击过程的动态特性分析
2017-10-14胡均平李科军
胡均平,李科军
考虑打桩反弹的组合锤头冲击过程的动态特性分析
胡均平,李科军
(中南大学机电工程学院,湖南长沙,410083)
针对打桩过程中桩体容易损坏的现象,提出一种在锤体内腔填充质量块的组合锤头打桩的新型锤击模型。运用键合图理论对锤击系统建模,为模拟打桩反弹时各质量块与垫层接触、分离的非线性特性,引入开关类量的键合图元件功率结型结构(SPJ),采用集中参数搭建锤击系统的键合图模型,据此建立可统一表达系统所有运动状态的数学模型。利用量纲一分析法推导锤击力的数值解,并基于Matlab软件仿真分析填充质量块和垫层参数对锤击力的影响。通过试验验证该模型的准确性。研究结果表明:采用组合锤头时,锤击力波形出现2个峰值,且峰值减小,这不仅可以保护桩体,而且可提高能量传递效率;各参数中,填充质量块和锤垫对锤击性能的影响最大,砧坐垫的影响次之,桩垫的影响最小。该模型可用于锤击系统的参数优化研究及动态特性分析。
组合锤头;键合图;反弹;锤击力
液压打桩锤以液压能为动力,提起锤头后通过快速泄油或反向供油使锤头加速下降,将桩体打入土 壤[1]。与柴油锤、振动锤和压桩机等桩工机械相比,液压锤是一种振动小、噪声低、无油烟污染和施工适用性强的产品,而且锤击频率、锤击行程可控,在桩基施工中发挥越来越重要的作用[2−3]。锤击系统作为打桩锤的核心装置,其工作性能直接关系到打桩质量及打桩效率。为掌握桩锤冲击过程的动态特性对沉桩效率的影响规律,有必要对锤击系统建立完整、准确的数学模型。TAKE等[4−5]用集中质量块表示桩锤、砧座,用无质量弹簧表示锤垫、桩垫,建立普通桩锤锤击力的解析模型,并仿真分析了垫层参数等对锤击力的影响。方治华等[6]基于ABAQUS软件对混凝土预制桩的打桩过程进行动态模拟,得到了打桩机械参数、桩体参数对打桩过程的影响规律。罗春雷等[7]针对振动桩锤在沉桩作业过程中的“跳机”问题,建立了分段非线性的二自由度模型,对“跳机”现象产生的根本原因进行了仿真分析和试验研究。为提高桩锤冲击的贯入量、增加垫层使用寿命及使桩体不受损坏,杨永海等[8−10]研究了金属颗粒填充桩锤的锤击模型,发现金属颗粒的加入能引发二次冲击,生成矩形锤击力波形,这可以降低锤击力最大峰值及提高冲击过程的能量转化率,但这些研究中,有的对锤击模型建模时忽略了冲击过程中金属颗粒本身的影响[8],有的采用接触刚度模拟金属颗粒与锤体的相互作用,但形状不规则的金属颗粒给接触刚度的计算及设计带来了困难[9],而且都没有考虑打桩反弹时各质量块与垫层之间接触、分离的非线性特性对锤击系统工作性能的影响。为此,本文作者用质量块代替金属颗粒填充到锤体内腔,并在质量块和锤体内腔的上、下接触面之间放置垫层,组成一种新型锤击模型。为模拟打桩反弹时锤击系统从一个工作状态过渡到另外一个工作状态的非连续性工作过程,引入开关类量的键合图元件功率结型结构(SPJ),采用集中参数建立可统一表达锤击系统所有运动状态的键合图模型,并利用该模型仿真分析填充质量块和垫层参数对锤击力的影响规律,以便为锤击系统的设计和优化提供依据。
1 功率结型结构
现实中,研究的系统多为混杂系统,即系统中同时存在连续元件和离散元件。建立混杂系统键合图模型的关键就是对系统中具有离散特性的元件尤其是开关元件进行键合图描述。KARNOPP等[11]提出用转换器MTF来描述系统中的离散行为,当开关处于闭合状态时,MTF的调制参数取值为1;当开关处于断开状态时,调制参数取值为0,但在开关元件处于断开状态时,结点和系统的连接很容易断开。BORUTZKY[12]在KARNOPP等[11]的研究基础上,提出增加1个阻性元件调制转换器MTF连接以描述系统离散行为。该方法能保证键合图模型的因果关系不随物理结构的变化而变化,但的引入带来了损耗,使得开关元件不再呈理想特性,而且的变化范围极大,容易导致系统模型在数值上呈刚性,增加仿真计算时间。为克服上述缺点,UMARIKAR等[13]提出一种表达开关类量的新键合图元件1s结,即功率结型结构(switch power junction, SPJ)。该元件分别在基本结型元件1结和0结的基础上,增加了2个相互排斥的流通口和势通口,通过信号键控制2个相互排斥的流通口或势通口的生效。1S和0S结因果示意图如图1所示。从图1(a)可见:1s结连接了2个流结,并且由1对布尔变量控制;变量1与键1相连,变量2与键2相连;系统的信号键决定了与布尔变量相连的键是否生效。当1为1时,键1生效,1(流变量)为1s结的唯一流输入;当2为1时,键2生效,2(流变量)为1s结的唯一流输入。因此,1s结上的流为11+22,通过1s结的各势变量之和为零,组成关系式如下:
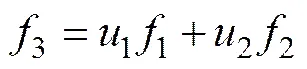
(2)
(3)
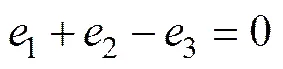
类似地,从图1(b)可见0s结上有2个势输入,0s结上的势为11+22。通过0s结的各流变量之和为0,组成关系式如下:
(5)
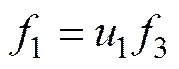
(7)
(8)
根据需要,运用布尔算法,可以得1,2,…,u等个变量推导出1s结和0s结上的组成关系式。

(a) 1s结;(b) 2s结
2 锤击系统建模
假设桩体为无限长杆,据一维波动力学理 论[14−16],桩顶的锤击力与波速成正比,即=(式中:为桩的波阻,与桩的弹性模量p、桩的横截面积p及波在桩内的轴向传播速度p有关,=pp/p)。因此,建模时桩体可以用1个阻尼器等效替代。
组合锤头的锤击模型如图2所示。分别用不同的集中质量块表示填充质量、锤体、砧座,用并联的弹簧、阻尼器表示砧坐垫,用弹簧表示锤垫、桩垫,用阻尼器表示桩体。
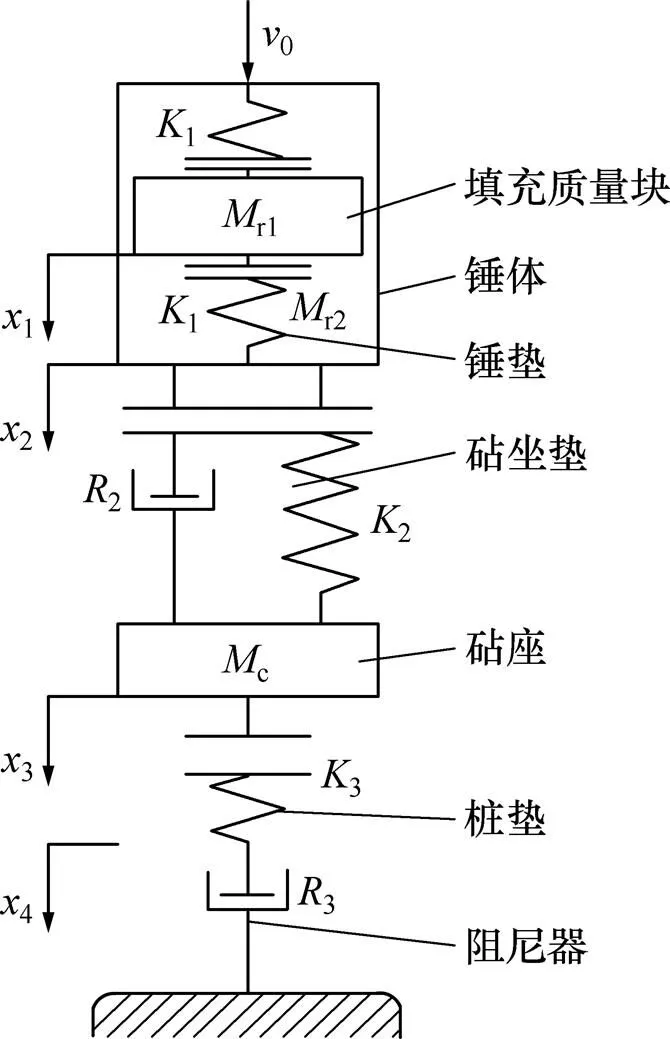
图2 组合锤头锤击模型
2.1 数学模型
结合前面的功率结型结构及组合锤头锤击模型,建立图3所示的锤击系统键合图模型。在锤头冲击过程中,重力相对于锤击力要小得多,因此,建模时不予考虑。为避免因果矛盾,在1()结上,代表桩体等效阻尼器的元件上的势变量为输入、流变量为输出。图3中:r1为填充质量块的质量;r2为锤体的质量;a为砧座质量;1,2和3分别为锤垫、砧坐垫、桩垫的刚度系数;2和3分别为砧坐垫阻尼系数和桩体阻尼系数。各惯性、容性及阻性元件都具有线性特征,利用各结约束条件及标定的因果关系,可以推导出系统的状态方程:
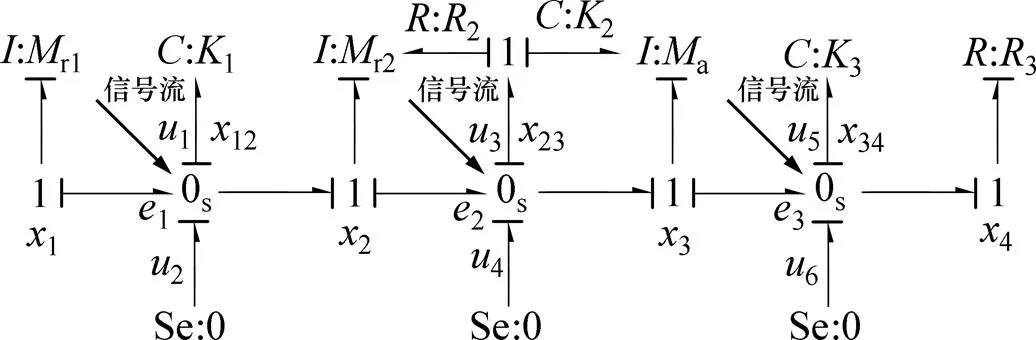
图3 锤击系统键合图模型
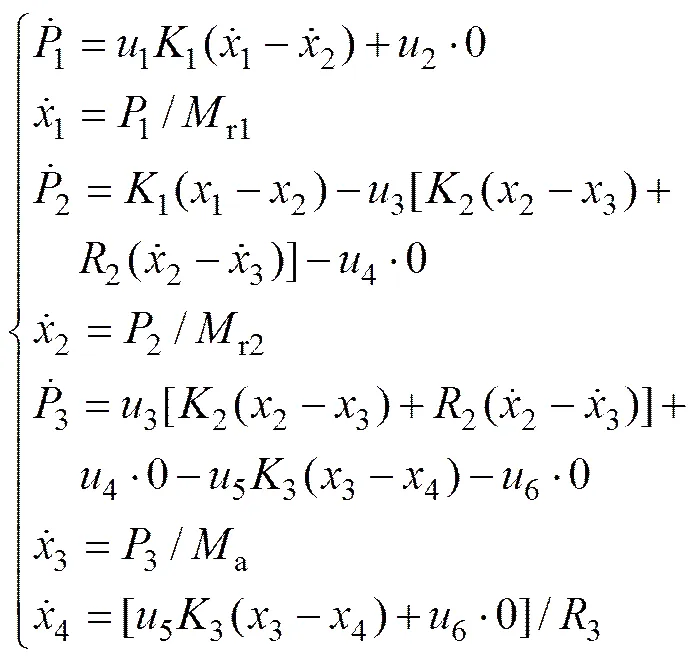
式中:1,2和3分别为填充质量块、锤体、砧座的动量;,,和分别为填充质量块、锤体、砧座阻尼器的运动速度。
由于填充质量块上下接触面都放置了垫层,可以认为打桩过程中填充质量块始终与弹簧1保持接触,仿真计算时1取1,2取0。式(9)中其他2对布尔变量的取值和转换条件如图4所示,可知锤击系统有22即4种运动状态。需要指出的是:并不是每种运动状态都会发生,但该式统一表达了锤击过程中可能出现的所有运动状态,且键合图模型的因果关系在系统处于任何运动状态时均保持不变。

图4 锤击系统运动状态转换
2.2 参数量纲一化分析
为便于研究各参数变化对锤击系统的反弹和锤击力影响,对式(9)的参数进行量纲一化处理。选择质量r(r=r1+r2)、桩体等效阻尼3及锤击初速度0为基本量,可得量纲一时间为*=3/r;量纲一质量为,,;量纲一弹簧刚度为,,;量纲一力为,,;量纲一动量为,,;量纲一阻尼为,;量纲一位移为,,,。将以上量纲一参数代入式(9)可得:
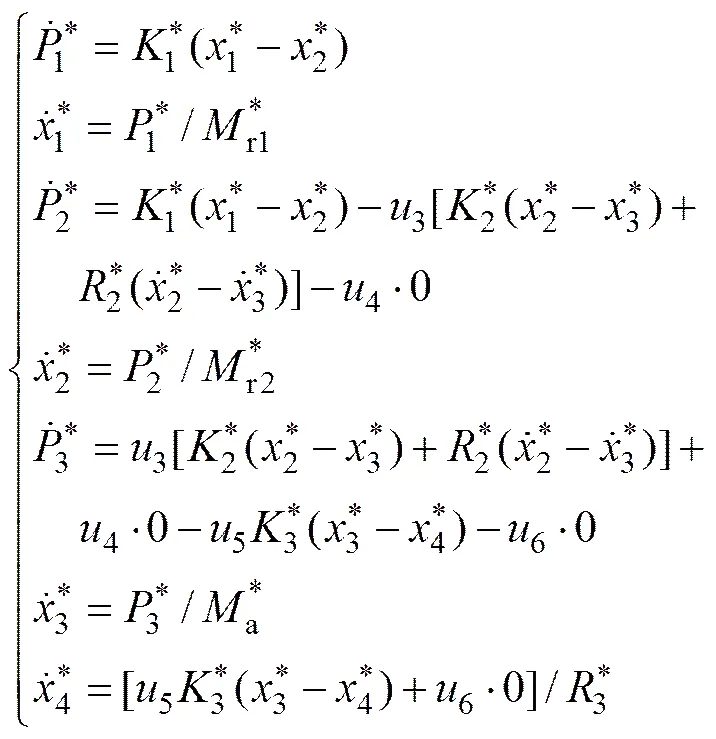
在桩锤撞击桩体瞬间,锤体及腔内填充质量块的初始速度均为0,对应的量纲一速度为:,。砧座、桩体的初始速度、加速度均为0,因此,锤击系统的初始条件为
(11)

3 打桩反弹影响
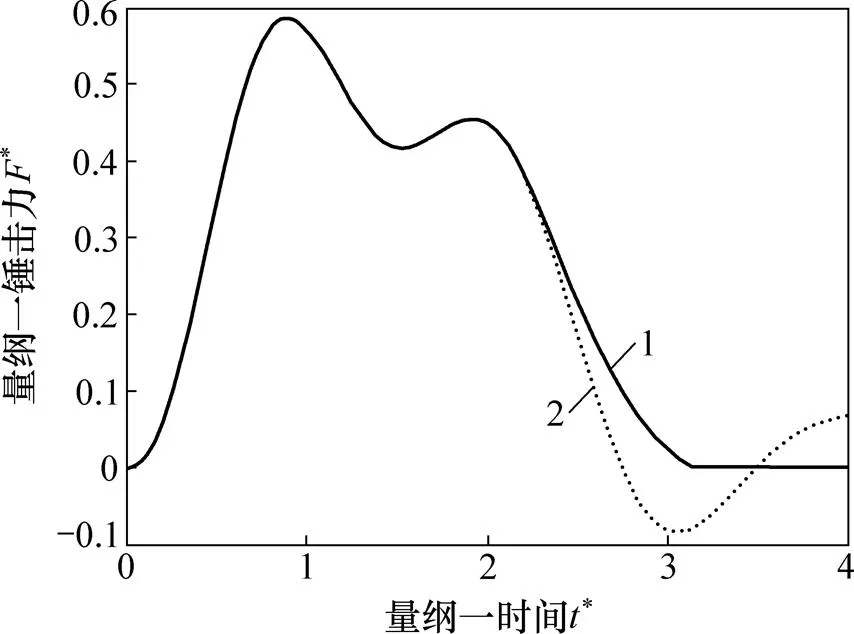
1—考虑打桩反弹;2—考虑打桩反弹。
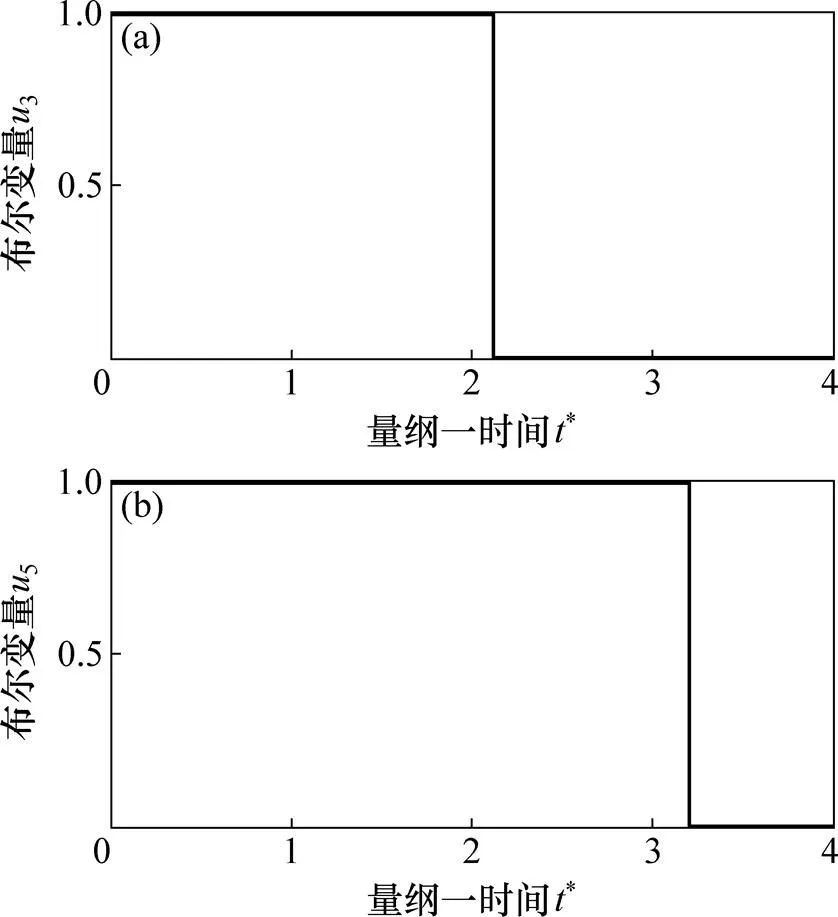
(a) u3;(b) u5
4 参数对锤击系统动态特性的影响
利用建立的数学模型可研究各参数组合对锤击系统动态特性的影响。由状态方程式(10)可知:桩顶的锤击力主要由7个量纲一参数确定,即填充质量块质量、锤体质量、砧板质量、锤垫刚度系数、砧坐垫刚度系数、阻尼系数和桩垫的刚度系数。
4.1 填充质量块参数
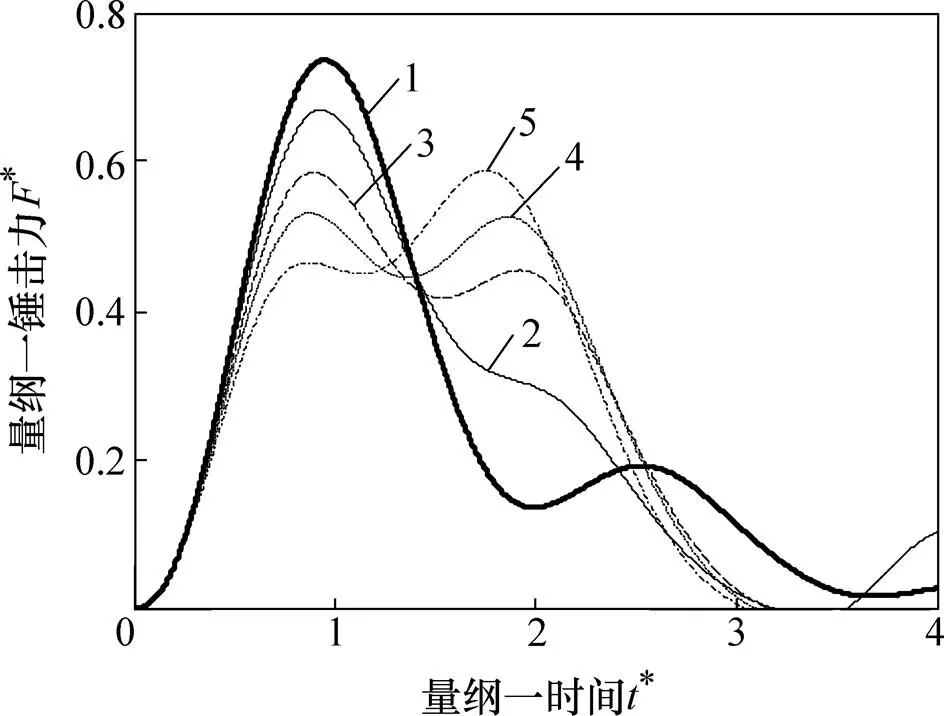
Mr1*:1—0;2—0.3;3—0.5;4—0.6;5—0.7。
4.2 垫层参数
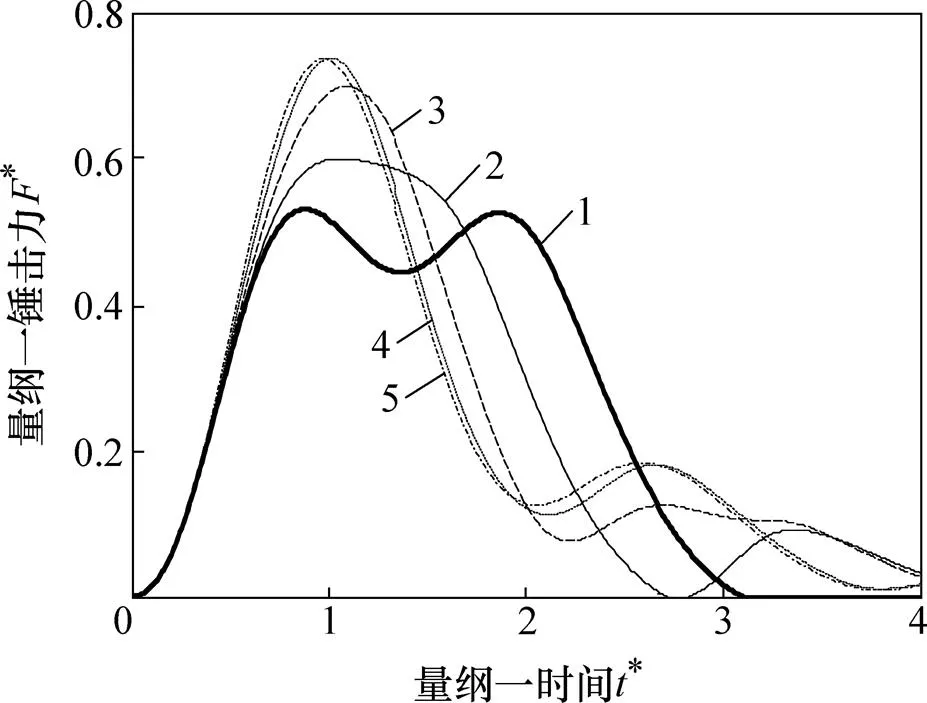
K1*:1—2;2—4;3—8;4—16;5—32。
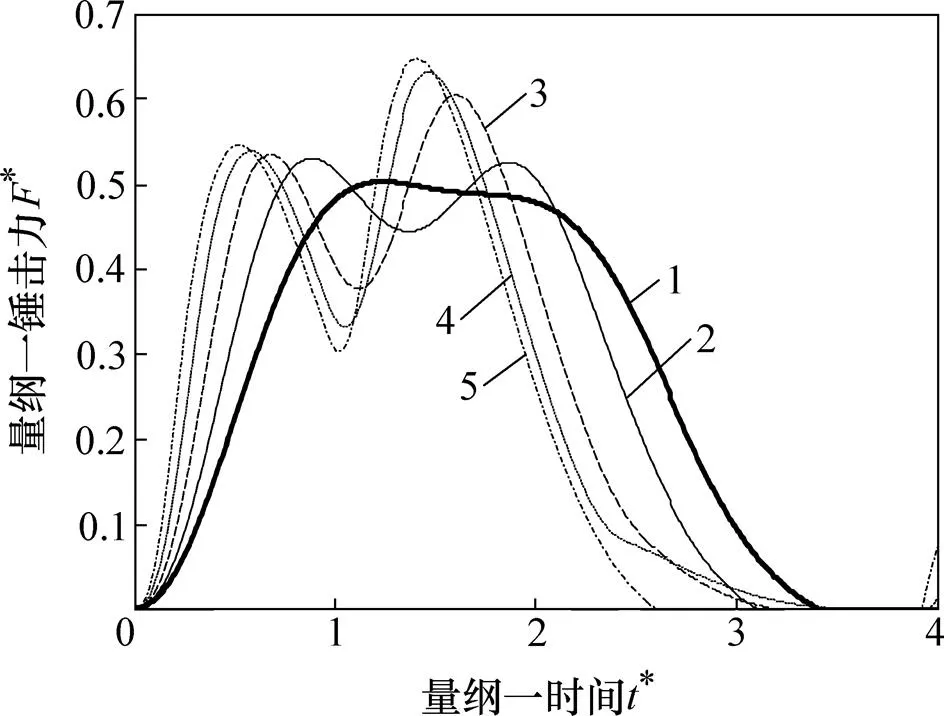
K2*:1—2;2—4;3—8;4—16;5—32。
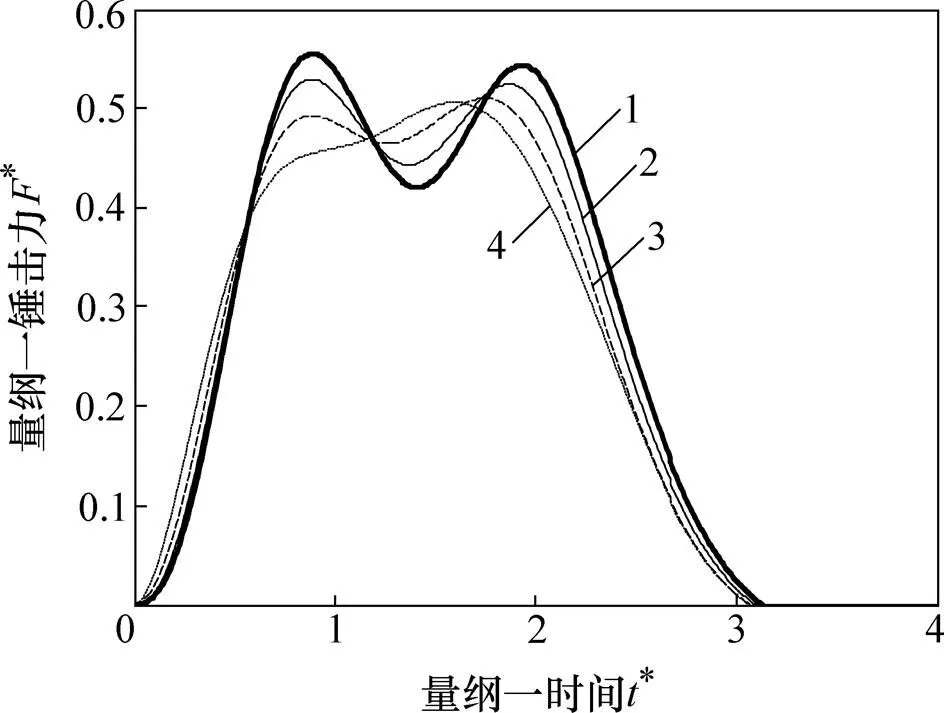
R2*:1—0.1;2—0.2;3—0.4;4—0.8。
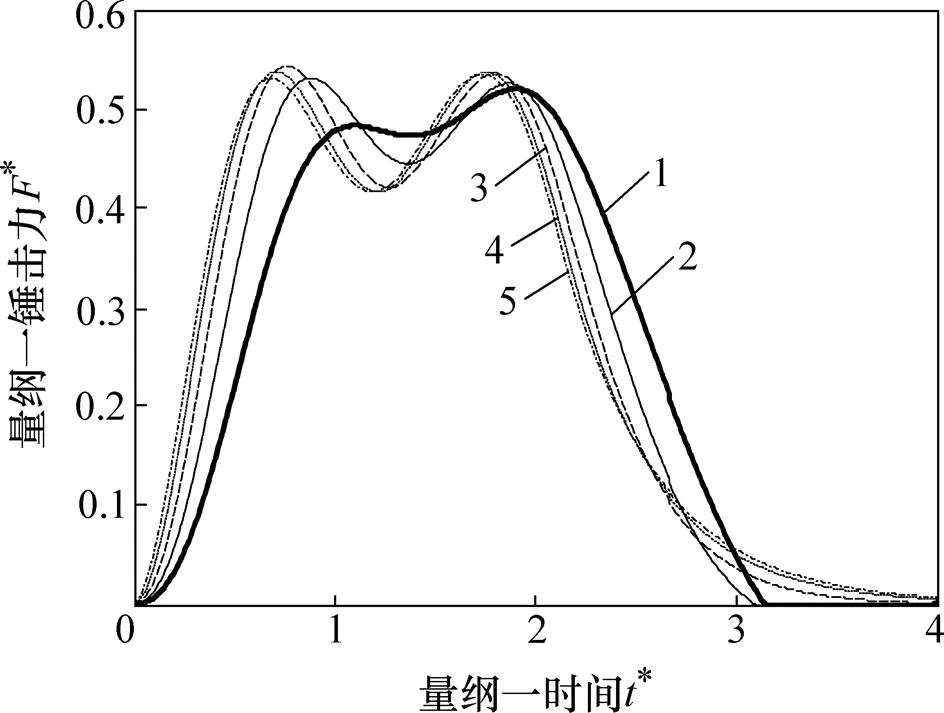
K3*:1—2;2—4;3—8;4—16;5—32。
5 试验
为验证组合锤头打桩效果及数学模型的准确性,采用湖南长河机械有限公司生产的ZCYL20-6液压打桩机对锤击力进行测量。填充质量块、锤体、砧座的质量分别为3.0,3.0和1.5 t;锤垫、砧坐垫和桩垫刚度分别为1×109,4×109和2×109N/m;桩锤初速度为5.6 m/s。桩采用预应力高强混凝土管(PHC)桩,AB型,外直径为500 mm,壁厚为125 mm,长为13 m,弹性模量约为36.0 GPa;应力波在桩身中传播的速度为3.8~4.0 km/s;桩体最大承载力为5.6 MN左右。普通锤头和组合锤头产生的锤击力见图12。从图12可见:普通锤头锤击力超过了桩体承载力,容易损坏桩体,而组合锤头锤击力峰值要小,始终没有穿越桩体最大承载力所在的参照线,保护了桩体,且锤击力波形接近矩形,增加了有效工作持续时间;组合锤头锤击力的计算值和实测值具有相同的变化趋势,2次冲击的锤击力峰值也较接近,表明建立的数学模型是正确、可行的。
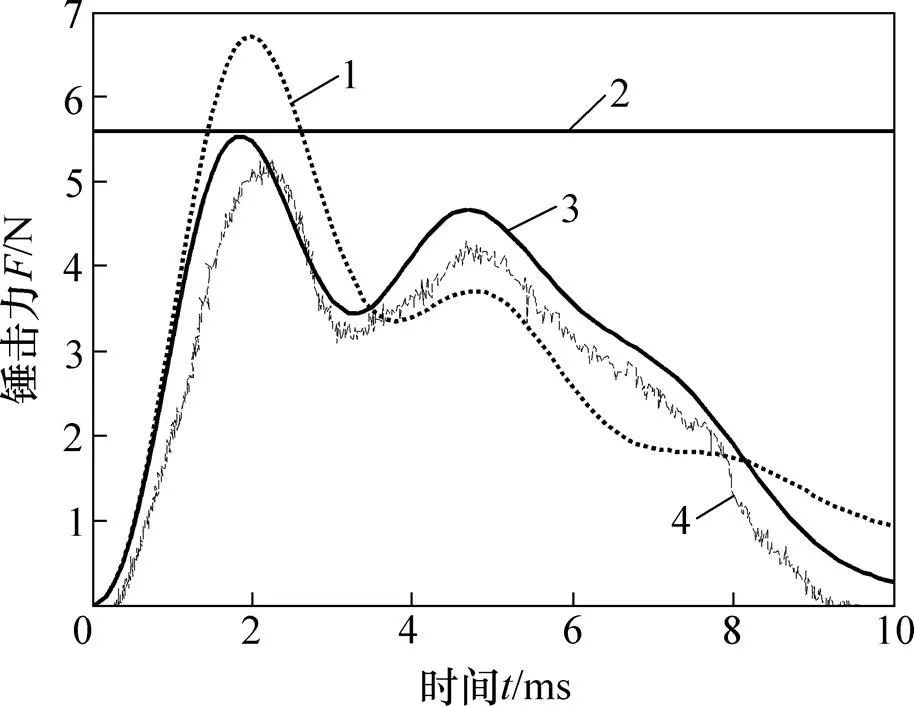
1—普通锤头计算值;2—桩体最大承载力;3—组合锤头计算值;4—组合锤头实测值。
6 结论
1) 提出一种采用组合锤头打桩的新型锤击模型,为模拟冲击过程中打桩反弹的运动状态,引入开关类量的键合图元件功率结型结构(SPJ),采用集中参数建立了全面反映系统运动状态的键合图模型;比较分析了考虑打桩反弹、不考虑打桩反弹2种数学模型的锤击力仿真曲线。所提出的模型能更好地模拟打桩的锤击机理。
2) 与普通锤头相比,组合锤头能产生2次冲击,锤击力峰值减小,锤击力波形更接近矩形,有效冲击时间增加,这不仅可以保护桩体,而且能提高能量传递效率;各参数中,填充质量块和锤垫对锤击性能的影响最大,砧坐垫的影响次之,桩垫的影响最小。
3)所建立的数学模型能较准确地反映各参数对锤击力的影响规律,对完善锤击系统设计理论和提高打桩效率有参考价值。
[1] 严东兵, 胡均平, 梅丽仿, 等. 氮爆式液压打桩锤结构原理与分析[J]. 工程机械, 2009, 40(4): 35−38. YAN Dongbing, HU Junping, MEI Lifang, et al. Structural principle and analysis of nitrogen-exploding type hydraulic pile hammer[J]. Construction Machinery and Equipment, 2009, 40(4): 35−38.
[2] GUO Y, HU J P, ZHANG L Y. Finite-element analysis of multi-body contacts for pile driving using a hydraulic pile hammer[J]. Proceedings of the Institution of Mechanical Engineers: Part C, 2011, 225(5): 1153−1161.
[3] 刘成沛. 液压打桩锤压力反馈配流系统及回油特性研究[D]. 长沙: 中南大学机电工程学院, 2012: 1−10. LIU Chengpei. Research on pressure feedback flow distribution system and oil return characteristics of hydraulic pile hammer[D]. Changsha: Central South University. School of Mechanical and Electrical Engineering, 2012: 1−10.
[4] TAKE W A, VALSANGKAR A J, RANDOLPH M F. Analytical solution for pile hammer impact[J]. Computers and Geotechnics, 1999, 25(2): 57−74.
[5] 谢永建, 朱合华, 王怀忠, 等. 打桩锤击模型的解析算法[J]. 岩石力学与工程学报, 2005, 24(1): 171−176. XIE Yongjian, ZHU Hehua, WANG Huaizhong, et al. Analytical solution for model of pile hammer impact[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(1): 171−176.
[6] 方治华, 程建华. 打桩过程的非线性有限元分析[J]. 内蒙古科技大学学报, 2009, 128(2): 184−188. FANG Zhihua, CHENG Jianhua. The non-linear finite element analysis in the process of piling[J]. Journal of Inner Mongolia University of Science and Technology, 2009, 128(2): 184−188.
[7] 罗春雷, 吴伟传, 丁吉, 等. 振动沉桩过程“跳机”现象动力学特性[J]. 中南大学学报(自然科学版), 2012, 43(11): 4274−4279. LUO Chunlei, WU Weichuan, DING Ji, et al. Dynamic characteristics of vibratory hammer “dancing” in piling[J]. Journal of Central South University (Science and Technology), 2012, 43(11): 4274−4279.
[8] 杨永海, 吕景忠, 隋振, 等. 加速下落冲击式液压桩锤设计[J]. 农业机械学报, 2005, 36(5): 150−152. YANG Yonghai, LÜ Jingzhong, SUI Zhen, et al. Design of Accelerated Impact Pile Hammer[J]. Transactions of the Chinese Society for Agricultural Machinery, 2005, 36(5): 150−152.
[9] 胡均平, 郭勇, 宋光伟, 等. 金属颗粒填充桩锤锤击模型的数值分析[J]. 中国公路学报, 2010, 23(2): 122−126. HU Junping, GUO Yong, SONG Guangwei, et al. Numerical analysis for impact model of pile hammer filled with metal particles[J]. China Journal of Highway and Transport, 2010, 23(2): 122−126.
[10] 刘德顺, 李夕兵, 朱萍玉. 冲击机械动力学与反演设计[M]. 北京: 科学出版社, 2007: 38−75.LIU Deshun, LI Xibing, ZHU Pingyu. Dynamics and inverse design of impact machines[M]. Beijing: Science Press, 2007: 38−75.
[11] KARNOPP D C, MARGOLIS D L, ROSENBERG R C. System dynamics: modeling, simulation, and control of mechatronic systems[M]. New York: John Wiley & Sons, 2012: 17−33.
[12] BORUTZKY W. Bond graph methodology: development and analysis of multidisciplinary dynamic system models[M]. Berlin: Springer, 2010: 305−349.
[13] UMARIKAR A C, UMMLAND L. Modeling of switching systems in bond graphs using the concept of switched power junctions[J]. Journal of the Franklin Institute, 2005, 342(2): 131−147.
[14] 苗润田. 基于波动力学的凿岩机效率研究[D]. 长沙: 中南大学机电工程学院, 2006: 4−22. MIAO Shuntian. The research of rock drill efficiency based on the wave mechanics[D]. Changsha: Central South University. School of Mechanical and Electrical Engineering, 2006: 4−22.
[15] 雷林源. 桩基动力学[M]. 北京: 冶金工业出版社, 2000: 35−41. LEI Linyuan. Pile foundation dynamics[M]. Beijing: Metallurgical Industry Press, 2000: 35−41.
[16] 刘德顺, 杨志高, 杨书仪. 电锤冲击系统的波动力学研究[J]. 振动工程学报, 2013, 26(6): 864−870. LIU Deshun, YANG Zhigao, YANG Shuyi. Wave mechanics for an electric hammer impact system[J]. Journal of Vibration Engineering, 2013, 26(6): 864−870.
(编辑 陈灿华)
Dynamic characteristics analysis of impact model of composite hammer considering rebound in piling
HU Junping, LI Kejun
(School of Mechanical and Electrical Engineering, Central South University, Changsha 410083, China)
In view of the phenomenon of pile body damage in the process of pile driving, the impact model of composite hammer filled with mass in the inner cavity was proposed. The lumped parameter method was used to establish the bond graph model of impact model, which introduced the concept of switched power junctions (SPJ) to represent the nonlinear characteristics of contact and separation between masses and cushions, and then the system equations were derived from the model in a unified way. The method of dimensionless analysis was used to analyze the effect of various parameters on the impact force within the Matlab environment. The model was verified experimentally. The results show that the composite hammer causes a lower crest and a longer effective impact time as it has more than one force wave, which also protects the pile body and improves the efficiency of energy transfer. The filling mass and the hammer cushion have the greatest effects on the performance of the hammer, the anvil cushion is the second, and the pile cushion is the smallest. The method can be used to the optimum design and dynamic analysis of the hammer impact system.
composite hammer; bond graph; rebound; hammer impact force
10.11817/j.issn.1672−7207.2017.02.012
TH113.1;U415.5
A
1672−7207(2017)02−0348−07
2016−02−10;
2016−04−22
国家自然科学基金资助项目(51175518);湖南省科技型中小企业技术创新基金资助项目(12C26214305029) (Project(51175518) supported by the National Natural Science Foundation of China; Project(12C26214305029) supported by Small and Mediu-sized Enterprise Technology Innovation Fund of Hunan Province)
李科军,博士研究生,从事液压机械与控制研究;E-mail:likejuncsu@126.com
