基于等维新息的GM（2,1）递推预测模型

岳赟，卢光跃，刘迪，董静怡



基于等维新息的GM（2,1）递推预测模型

岳赟，卢光跃，刘迪，董静怡

（西安邮电大学无线网络安全技术国家工程实验室，陕西西安 710121）

针对GM（2,1）白化方程的解影响其预测精度的问题，提出了一种新的预测模型——等维新息GM（2,1）递推预测模型。该模型通过其灰色微分方程推导出GM（2,1）递推预测模型的表达式，避免了对二阶白化方程进行求解，同时解决了差分方程与微分方程之间因转换而产生误差的问题，并结合等维新息的思想更新GM（2,1）递推预测模型的参数。最后通过实例验证了所提等维新息GM（2,1）递推预测模型的有效性和实用性。

GM（2,1）模型；白化方程；灰色微分方程；等维新息；递推预测模型

1 引言

如何挖掘缺乏统计规律的小样本预测系统的发展规律，一直是学术界的难点[1]。灰色系统（grey system）是20世纪80年代邓聚龙提出的一种针对小样本、贫信息、不确定性问题的方法。灰色系统理论以“部分信息已知，部分信息未知”的小样本、贫信息、不确定系统为研究对象，通过对“部分”已知信息的生成、开发，提取有价值的信息，实现对系统运行行为、演化规律的正确描述和有效监控[2]。

GM（2,1）模型作为灰色系统中最重要的预测模型之一，已广泛应用于经济、生态、科技、农业、生物等各个领域。GM（2,1）模型是由原始序列建立的二阶微分方程，有两个特征根，因此动态过程能反映出单调、非单调或摆动等多种情况[3]。然而实际求解过程中存在的近似误差会对算法性能带来影响，比如GM（2,1）模型用梯形公式近似代替背景值，以向前差商或向后差商近似代替灰导数，初始条件的选取缺乏合理性等。因此，诸多学者对GM（2,1）模型进行了改进和优化，参考文献[3]利用最小二乘法对模型的初始条件进行修正，降低了模型的预测误差；参考文献[4]利用新信息优先的原理来求解预测响应函数中的1、2，进而提高了模型的预测效果；参考文献[5]利用权值1、2对一阶灰导数和背景值进行加权组合，以提高模型的预测精度；参考文献[6]分别利用参数和对GM（2,1）模型的背景值进行修正，并对原始数据进行数乘变换，以此提高模型精度。

以上研究从不同角度对GM（2,1）模型进行改进，在一定程度上提高了GM（2,1）模型的预测精度。然而GM（2,1）模型存在解的多样性及离散模型与连续模型之间的近似替代问题，本文对GM（2,1）模型的参数估计、模拟及预测均采用离散形式的方程，从而推导出GM（2,1）递推模型，然后利用新息优先的思想不断更新建模用的原始数据，进而更新系统参数。

2 GM（2,1）模型

2.1 建模原理

作为灰色预测中最重要的模型，GM（2,1）是由原始数据序列建立的二阶微分方程，其时间响应函数有两个指数分量，主要适合对单一时间序列的系统进行模拟和预测。

记长度为的原始非负序列(0)={(0)(1),(0)(2),…,(0)()}，对其进行一次累减和一次累加生成，分别记为和(1)={(1)(1),(1)(2),…,(1)()}，其中，(1,2,3,…,)。据此构造背景值序列(1)={(1)(1),(1)(2), …,(1)()}，其中(2,3,…,)。

则称：

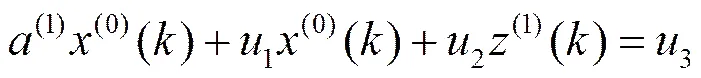
为GM（2,1）模型，其中u（=1,2,3）为待确定的系统参数。

式（1）对应的白化微分方程形式为：

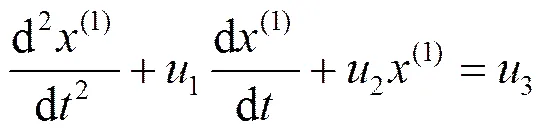
关于GM（2,1）常微分方程的解[7]有如下说明。

（2）齐次方程的通解有以下3种情况。

（3）常微分方程的特解有以下3种情况。

实际上绝大部分数据都是两个不相等的特征根，下面就以此为例说明求解的步骤。

设特征根是1、2，则上述微分方程的解为：

采用最小二乘原则求解1、2，使达到最小。

（5）

进而由克拉默法则求解1、2。

将1、2代入式（3），并在=（1,2,…,）处的值来逼近：

将式（6）累减还原，即可得到预测值：

，2,3,…,（7）

2.2 模型的检验

众所周知，拟合的精度是评判模型效果的核心指标。因此，灰色预测模型必须通过精度检验后再决定其是否可以用于模拟和预测。模型精度的检验方法主要有3种：残差检验法、后验差检验法和关联度检验法，其中残差检验法是最常用的方法。残差是实际值与模拟值之差，残差检验实际上检验的是模拟值与实际值之间偏离的程度[8]。残差检验步骤如下。

设原始序列(0)和模拟序列分别为：

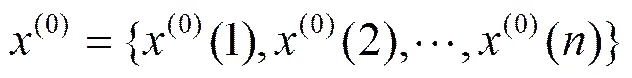
（9）

其绝对误差()和平均相对误差分别为：

（11）

当<10%且()<10%，称模型为残差合格模型。

GM（2,1）模型是由原始序列建立的二阶微分方程，有两个特征根，能动态地反映出单调、非单调或摆动等多种情况，然而在建模的过程中存在解的多样性及离散模型与连续模型之间的近似替代问题。

3 等维新息GM（2,1）递推模型

为了避免建模过程中存在解的多样性及离散模型与连续模型之间的近似替代问题，本文将提出一种新的GM（2,1）递推模型，该方法在建模过程中一直沿用差分方程的形式。将,代入式（1）得：

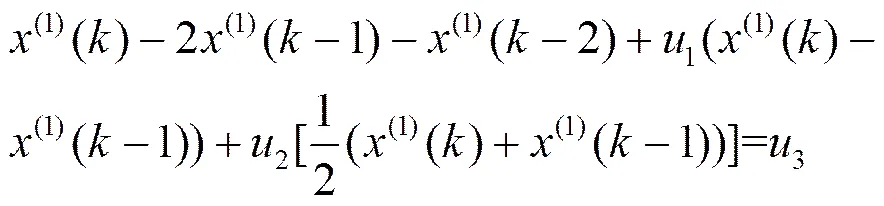
化简式（12）得：

（13）

易知：

（15）

式（14）减去式（15），整理得：

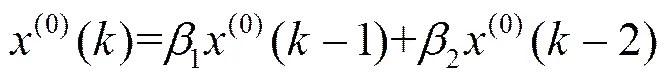
其中，(0)()为=时刻的模拟预测值，1和2为系统的待确定值，可利用最小二乘法求解。

GM（2,1）递推预测模型计算简单，不需对二阶微分方程进行求解，且避免了离散模型与连续模型之间的近似替代，从而提高了模型的预测精度。

GM（2,1）递推模型只能做逐步预测，在进行下一步预测时，需用到上一步预测的结果，每步预测的参数估计值1和2是个定数——由原始时序得到，随着预测步数的增加，其预测精度有可能较快下降。为了减缓预测精度下降的速度，本文采用等维新息递推预测模型提高其预测精度。

对于灰色系统而言，随着时间的推移，干扰系统的因素不断变化，系统的状态也在不断变化。传统灰色预测模型准确度较高的仅仅是原点数据以后的1~2个数据，越向未来发展，即越远离时间原点，模型的预测准确度越低。因此，必须引入已知信息来反映系统的变化和状态，或在无已知信息的情况下，用灰色信息来淡化灰平面的灰度，这种模型由于及时地引入了新的已知信息或灰色信息，删除旧的数据，能够比较准确地反映系统的变化状态，故称为新息灰色模型[9]。而灰色预测模型长期预测的有效性明显受到时间序列长短及数据变化的影响，数据序列太短，难以建立长期的预测模型；数据序列太长，系统受干扰的成分变大，不稳定因素增多，系统预测精度下降。所以等维新息GM（2,1）递推模型通过在GM（2,1）递推模型中加入等维约束条件，弥补了灰色系统模型的不足，有效地提高预测的精度[10]。

在原始序列(0)={(0)(1),(0)(2),…,(0)()}的基础上，去掉第一个数据(0)(1)，同时加入新的已知数据(0)(+1)，构成等维动态序列(0)={(0)(2),(0)(3),…,(0)(),(0)(+1)}，如此递补，依次递推，建立等维新息GM（2,1）递推预测模型。

综上，等维新息GM（2,1）递推预测模型的建模步骤如下。

步骤1 构造原始数据序列(0)={(0)(1),(0)(2),。

步骤2 将(0)代入式（16），求出1和2，建立GM（2,1）递推预测模型。

步骤3 计算+1时刻的预测值(0)(+1)。

步骤4 更新原始数据序列(0)，即令(0)= {(0)(2),(0)(3),…,(0)(),(0)(+1)}。

步骤5 返回步骤2，重复步骤2~4，直至计算完所有预测数据的预测值为止。

4 实例分析

1997年以来，中国互联网信息中心（CNNIC）已连续20年开展统计调查工作，并于每年1月、7月分两次发布统计报告，公布我国Internet上网计算机数、用户人数、用户分布、信息流量分布、域名注册等方面情况的统计信息，为我国信息化发展提供了重要的依据，也为政府、机构和企业各界提供重要决策参考。根据CNNIC第39次发布的《中国互联网络发展状况统计报告》，截至2016年12月，中国网民上网人数已过半，中国网民的人均周上网时长为26.4 h。本文选取CNNIC于2017年1月发布的第39次报告数据，分别以手机网民规模和网民人均周上网时长为例进行分析。

2008—2016年我国手机网民规模见表1，记表1的数据为原始序列(0)，该数据为单调递增序列，下面将利用GM（2,1）模型、参考文献[4]模型和等维新息GM（2,1）递推模型分别对(0)中的前7个数据建立相应的预测模型，后2个数据用来预测，以对比3种模型的预测精度。

对于GM（2,1）模型，利用2008—2014年的数据建立GM（2,1）模型，解得1=0.701 9、2=−0.098 2、1=24 107；对于参考文献[4]模型，灰色建模得1=0.338 3、2=−0.157 4、1=24 441；而对于等维新息GM（2,1）递推模型，首先建立GM（2,1）递推模型，解得1=1.842 1、2=−0.844 7，并得到2015年手机网民规模的预测值（见表2中“等维新息1”所在列），然后对原始数据进行一次等维新息处理，将2015年的实际值添加到原始序列中，同时删除2008年的数据，保持维度相同，重新建立GM（2,1）递推模型，解得1=1.549 6、2=−0.476 5，预测2016年手机网民规模（见表2中“等维新息2”所在列）。表2描述了3种模型对原始序列的的拟合值和相对误差。

表1 2008—2016年我国手机网民规模

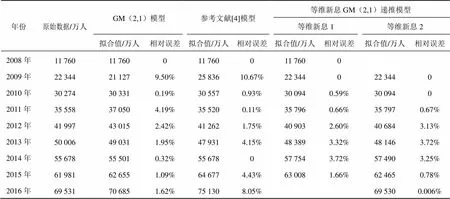
表2 3种模型对原始序列的拟合值和相对误差

由表2可知，GM（2,1）模型、参考文献[4]模型和等维新息GM（2,1）递推模型对原始序列进行一步预测的相对误差分别为1.09%、4.43%和1.66%，二步预测的相对误差分别为1.62%、8.05%和0.006%，2015年和2016年手机网民规模人数的平均相对误差分别为1.36%、6.24%和0.83%，从而表明本文所提的等维新息GM（2,1）递推模型的预测精度优于GM（2,1）模型和参考文献[4]模型。

2008—2016年中国网民人均周上网时长见表3，记表3的数据为原始序列(0)，该数据为摆动序列，下面将利用GM（2,1）模型、参考文献[4]模型和等维新息GM（2,1）递推模型分别对(0)中的前7个数据建立相应的预测模型，后2个数据用来预测，以对比3种模型的预测精度。

对于GM（2,1）模型，利用2008—2014年的数据建立GM（2,1）模型，解得1=−0.358 2、2=0.026 8、1=−5.523 1；对于参考文献[4]模型，灰色建模得1=−0.449 0、2=−0.034 8、1=21.397 0；而对于等维新息GM（2,1）递推模型，首先建立GM（2,1）递推模型，解得1=1.332 7、2=−0.312 5，并得到2015年网民人均周上网时长预测值（见表4中“等维新息1”所在列），然后对原始数据进行一次等维新息处理，将2015年的实际值添加到原始序列中，同时删除2008年的数据，保持维度相同，重新建立GM（2,1）递推模型，解得1=1.198 0、2=−0.193 2，预测2016年网民人均周上网时长（见表4中“等维新息2”所在列）。表4描述了3种模型对原始序列的拟合值和相对误差。

由表4可知，GM（2,1）模型、参考文献[4]模型和等维新息GM（2,1）递推模型对原始序列进行一步预测的相对误差分别为0.60%、28.02%和1.57%，二步预测的相对误差分别为4.82%、263.14%和1.07%，2015年和2016年网民人均周上网时长的平均相对误差分别为2.71%、145.58%和1.32%，参考文献[4]所提的模型对该数据的预测效果急剧下降，从而表明本文所提的等维新息GM（2,1）递推模型的预测精度优于GM（2,1）模型和参考文献[4]模型。

表3 2008—2016年中国网民人均周上网时长

表4 3种模型对原始序列的拟合值和相对误差

5 结束语

根据新息优先的思想，本文对GM（2,1）模型的参数估计、模拟及预测均采用离散形式的方程，并通过其灰色微分方程推导出GM（2,1）递推预测模型的表达式，从而建立等维新息GM（2,1）递推预测模型，该模型有效地避免了对二阶白化方程进行求解。最后，通过实例验证该改进模型的合理性，同时该模型有效地提高了预测精度。

[1] 吴利丰, 刘思峰, 姚立根. 含Caputo型分数阶导数的灰色预测模型[J]. 系统工程理论与实践, 2015, 35(5): 1311-1316.

WU L F, LIU S F, YAO L G. Grey model with Caputo fractional order derivative[J]. Systems Engineering Theory & Practice, 2015, 35(5): 1311-1316.

[2] 曾柯方. 几种灰预测模型的参数辨识与优化方法研究[D]. 南充: 西华师范大学, 2015.

ZENG K F. Identifying parameters and optimization method research of several grey prediction models[D]. Nanchong: China West Normal University, 2015.

[3] 李玲玲, 单锐, 崔红芳. 改进GM（2,1）模型的MATLAB实现及其应用[J]. 数学的实践与认识, 2011, 41(20): 179-183.

LI L L, SHAN R, CUI H F. The application of the improved GM(2,1) grey model using MATLAB[J]. Mathematics in Practice & Theory, 2011, 41(20): 179-183.

[4] XU N, DANG Y G. An optimized grey GM (2,1) model and forecasting of highway subgrade settlement[J]. Mathematical Problems in Engineering, 2015(1): 1-6.

[5] 牛思先, 陈鹏宇, 苏玉刚. 基于加权组合和最小二乘法改进的GM（2,1）模型[J]. 统计与决策, 2010(22): 28-30.

NIU S X, CHEN P Y, SU Y G. Improvement of GM (2,1) model based on weighted combination and least squares method[J]. Statistics and Decision, 2010(22): 28-30.

[6] 刘虹, 张岐山. 基于微粒群算法的GM(2,1, λ, ρ)优化模型[J]. 系统工程理论与实践, 2008, 28(10): 96-101.

LIU H, ZHANG Q S. GM (2, 1, λ, ρ) based on particle swarm optimization[J]. Journal of Systems Science and Information, 2008, 28(10): 96-101.

[7] 刘丽桑, 彭侠夫, 周结华. 两种改进的GM（2,1）模型及其在船舶横摇预报中的应用[J]. 厦门大学学报(自然科学版), 2011, 50(3): 515-519.

LIU L S, PENG X F, ZHOU J H. Two improved model of GM (2,1) and its application in ship rolling forecast[J]. Journal of Xiamen University(Natural Science), 2011, 50(3): 515-519.

[8] 卢懿. 灰色预测模型的研究及其应用[D]. 杭州: 浙江理工大学, 2014.

LU Y. The research and application of grey forecast model[D]. Hangzhou: Zhejiang Sci-tech University, 2014.

[9] ZHANG H, YANG Y. Application of equal dimension and new information gray prediction model in power load forecasting[C]// 2010 2nd International Conference on Signal Processing Systems (ICSPS), July 5-7, 2010, Dalian, China. New Jersey: IEEE Press, 2010: 196-200 .

[10] ZHANG Q, CHEN R. Application of metabolic GM (1,1) model in financial repression approach to the financing difficulty of the small and medium-sized enterprises[J]. Grey Systems, 2014, 4(2): 311-320.

GM (2,1) recursive forecasting model based on equal dimension and new information

YUE Yun, LU Guangyue, LIU Di, DONG Jingyi

National Engineering Laboratory for Wireless Security, Xi’an University of Posts and Telecommunications, Xi’an 710121, China

Aiming at the problem that the solution of GM (2,1) whitening equation affects its prediction accuracy, a new prediction model dubbed GM (2,1) recursive prediction model of equal dimension new information was proposed. The model was deduced from the grey differential equation of GM (2,1) mode, which could avoid solving the second-order whitening equation, solve the problem that the errors between equations and differential equations for conversion, and update the model parameters combining the idea of equal dimension and new information. Both the simulation and analysis of the example demonstrate that the proposed method is more effective and practical.

GM (2,1) model, whitening equation, grey differential equation, equal dimension and new information, recursive forecasting model

TP391.9

A

10.11959/j.issn.1000−0801.2017112

2017−02−22；

2017−04−20

陕西省工业科技攻关资助项目（No.2016GY-113，No.2015GY-013）；陕西省教育厅专项科研计划基金资助项目（No.16JK1704）

Industrial Research Project of Science and Technology Department of Shaanxi Province of China (No.2016GY-113, No.2015GY-013), Shaanxi Provincial Department of Education Special Research Project of China (No.16JK1704)

岳赟（1989−），男，西安邮电大学无线网络安全技术国家工程实验室硕士生，主要研究方向为数据分析。

卢光跃（1971−），男，西安邮电大学无线网络安全技术国家工程实验室教授，主要研究方向为信号与信息处理、认知无线电、数据分析等。

刘迪（1991−），男，西安邮电大学无线网络安全技术国家工程实验室硕士生，主要研究方向为数据分析。

董静怡（1992−），女，西安邮电大学无线网络安全技术国家工程实验室硕士生，主要研究方向为数据分析。