变压器绕组辐向稳定性研究
2017-10-13胡忠平廖福旺
胡忠平 廖福旺,2 兰 生
变压器绕组辐向稳定性研究
胡忠平1廖福旺1,2兰 生1
(1. 福州大学电气工程与自动化学院,福州 350108;2. 国网福建省电力有限公司电力科学研究院,福州 350007)
随着电力系统容量的不断增加,短路故障产生的电动力会引起变压器绕组变形等辐向稳定性的问题,有必要对变压器的绕组进行屈曲分析和弹塑性力学分析。本文采用ANSYS软件对中压侧三相短路状下变压器绕组进行屈曲和弹塑性力学分析,针对50MVA三绕组主变建模,获取中压绕组辐向安全稳定系数。通过事故实例予以验证,此方法对变压器短路影响分析具有一定参考价值,还可对大型变压器的设计及装配带来一定的借鉴意义。
电力变压器;场路耦合;电磁力;屈曲分析;弹塑性力学
随着电力系统容量及变压器单台容量的不断增大,变压器绕组的变形、抗短路能力不足等问题引起了人们广泛的关注,因此亟需进一步研究和优化完善变压器绕组的稳定性。
为此,刘兴平等人[1]利用在线测量不同负荷时的一次、二次侧电压电流的方式计算变压器的短路电抗值用以检测变压器绕组的变形。对于检测变压器绕组的变形及病灶位置,刘效真等人[2]通过对变压器的直流电阻、油色谱的数据的综合来判断。刘航宇等人[3]采用暂态短路电流计算方法和有限元的方法推导出电缆金具的电动力公式并对公式进行了修正。Amit Bakshi[4]采用漏磁场轴对称的有限元分析方法计算出漏磁场及电动力并将绕组视为两端固支的梁,在此基础上利用线性屈曲理论分析其稳定性。Ahn H M[5]在建立单相变压器三维模型时已按照实际情况,将高、低压绕组分成指定的段数,然后通过场-路耦合方法对电磁力进行了数值计算。王录亮[6]在建立二维模型时综合考虑了绕组间的油道、绝缘等因素,在此基础上计算出绕组的短路电磁力、分析了绕组的辐向稳定性。刘军等人[7]利用FLD漏磁场有限元软件计算出了110kV变压器的静态、动态短路电磁力,并用经验公式加以比较和验证。白永刚等人[8]分析了自耦变压器绕组与外电路的磁电联系,然后计算出公共绕组出口处发生短路时的电磁力大小,并在此基础上计算出串联绕组载荷拉伸位移量,用以研究变压器绕组的辐向稳定性。姜山[9]利用瞬态漏磁场的计算方法计算出二维对称变压器模型的漏磁场,并且详细介绍了变压器绕组的受力情况、抗短路能力等。周国伟等人[10]通过虚功原理推导出变压器轴向短路电磁力和由轴向高度微量变化引起的电抗变化表达式。
本文以一工程主变(容量为50MVA)进行分析,按照变压器的实际参数,利用ANSYS软件对中压侧绕组二维建模并绘制出辐向电磁力分布;在对分析完线性屈曲的前提下再对绕组进行非线性屈曲分析,以获得最接近于实际的临界载荷值;将材料的特性等相关因素考虑在内,利用ANSYS对绕组进行弹塑性力学分析,求取出绕组的冲击累积效应后的位移量;最后将仿真出的结果与省电科院提供的该主变故障分析报告相比较。
1 变压器建模与电磁力的求解
1.1 场-路耦合理论
本文研究主变的是在额定分接运行时,中压侧发生三相短路的故障。按照实际参数对绕组的各个线饼建模,而绕组的匝数、占空比、导线截面积等相关参数会通过实常数的方式赋予。变压器的内部采用磁场,外部采用电路的连接方式,在对每个有限元单元计算时需将磁场和电场分别进行耦合。
低压侧绕组应满足的约束方程组为

式中,JLiSKel依次表示为低压侧绕组中第个线饼的矢量磁位、电流密度、匝数、截面积、占空比、感应电动势、等效电阻、等效漏感、线饼长度;s1为低压侧线路部分的阻抗;1()为变压器低压侧额定电压。
中压侧绕组应满足的约束方程组为

式中,JLjSKel依次表示为中压侧绕组中第个线饼的矢量磁位、电流密度、匝数、截面积、占空比、感应电动势、等效电阻、等效漏感、线饼长度;2()为变压器中压侧的额定电压;为中压侧的漏阻抗。
高压侧绕组应满足的约束方程组为

式中,JLkSKel依次表示为高压侧绕组中第个线饼的矢量磁位、电流密度、匝数、截面积、占空比、感应电动势、等效电阻、等效漏感、线饼长度;s3为高压侧线路部分的阻抗;3()为变压器高压侧额定电压。
变压器油区域的约束方程为
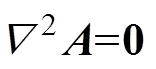
1.2 变压器模型的建立
该主变的联结组号为YNyn0d11,额定电压与分接范围为,变压器绕组的相关技术参数见表1。不同运行条件下的短路阻抗百分比见表2。
为了能够在建模时简化模型,需考虑变压器的结构和磁路等特征,可作出如下假设:

表1 变压器绕组的技术参数

表2 不同运行条件下的短路阻抗百分比/%
1)不考虑导线的涡流去磁效应。
2)有限元分析和求解时认为导线及其他区域的电导率和磁导率不变。
3)变压器导磁材料的磁导率按照实际磁滞曲线赋予。
可将上下铁轭和旁轭等效为长方形,所建立的模型如图1所示。

图1 变压器有限元模型
1.3 短路电流的计算
一般情况下,变压器发生短路时电流会激增,尤以发生三相短路故障时最为恶劣。获得短路电流的通解为

式中,1为短路电流的稳态分量;2为短路电流的暂态分量;为电压源初相角;d为变压器等值漏感系数;d为等效电阻。
通过有限元分析得到通过该主变中压侧绕组上的短路电流变化曲线如图2所示。

图2 短路电流随时间变化曲线
从图2知在时间=0.01s时电流达到峰值,该峰值电流为13679.03A,该峰值是中压侧在额定分接情况下的额定电流的18.246倍,最后达到的短路电流的稳态值为8555.29A。而省电科院提供的该台变压中压侧电流的录波波形如图3所示,该峰值电流与ANSYS仿真出的结果基本相吻合。

图3 变压器中压侧录波波形
1.4 电磁力的计算
获得的短路电流(密度)代入矢量泊松方程可得到矢量磁位。


故变压器绕组的辐向电磁力为
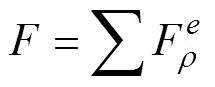
根据不同时刻磁密、电流值的大小,依次带入上述公式可计算出不同时刻、不同位置处的辐向电磁力。绘制出中压侧绕组的辐向电磁力曲线如图4所示。
从辐向电磁力的三维图中可以发现:
1)辐向的电磁力在最初的几个ms内非常小,然后随着时间的增长快速的递增直至达到峰值。
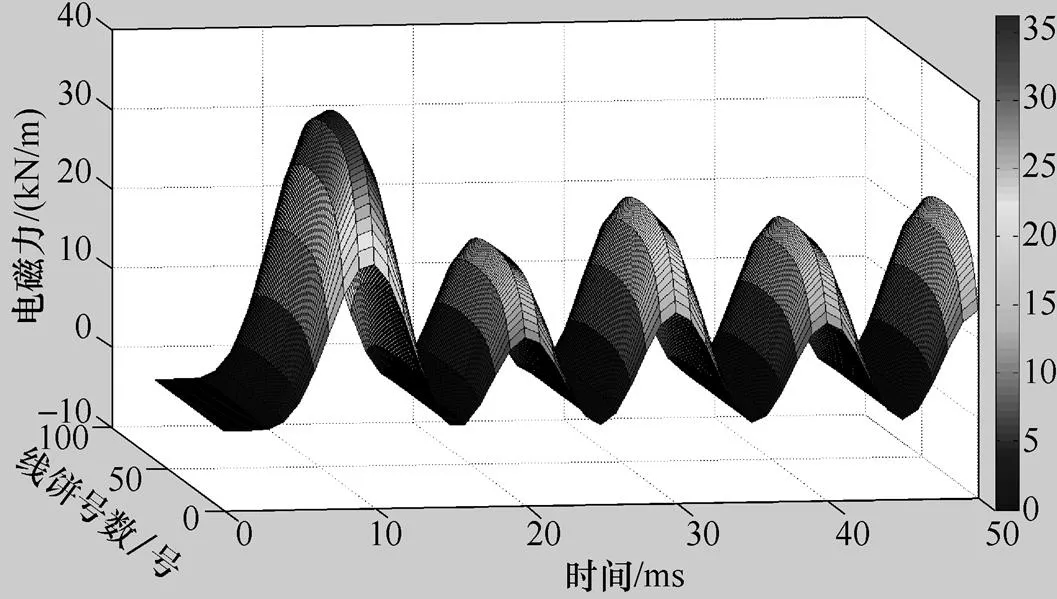
图4 中压侧绕组辐向电磁力分布图
2)中压侧每个线饼辐向电磁力的变化趋势与短路电流变化趋势相仿,即各个线饼所受电磁力均在=0.01s时达到峰值。
3)当时间固定时,变压器的绕组的中部附近的电磁力的值要明显大于端部的值。
根据以上可得中压侧绕组第32号线饼的电磁力最大,现将其绘制如图5所示,可得该线饼的最大电磁力为36.22kN/m。

图5 第32号线饼承受的电磁力变化图
2 绕组的非线性屈曲分析
2.1 非线性屈曲理论
本文运用弧长法[13]对绕组进行非线性屈曲分析。该方法需要引入一个载荷因子,此时New-Raphson公式应改写为
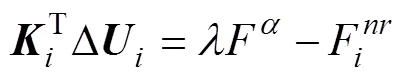
当子步数发展到,迭代发展到第步时,载荷因子增量为

将载荷因子增量带入(7)中并化简可得到
(11)
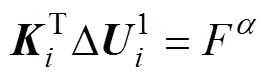
(13)
2.2 绕组的非线性屈曲分析
变压器绕组的分析模型主要有:两端固支的直梁、两端绞支的拱形梁、两端弹支的拱形机构和多跨模型[14-16]。由于两端固支模型不能考虑到导线与撑条间相对移动;两端绞支和两端弹支仅用一个转动系数且忽略其他诸多因素;同时考虑到实际变压器绕组的动力特性及其所受的动态分布载荷,本文采用多跨模型,对整个线饼进行分析研究,绕组模型如图6所示。在分析时需作以下说明。
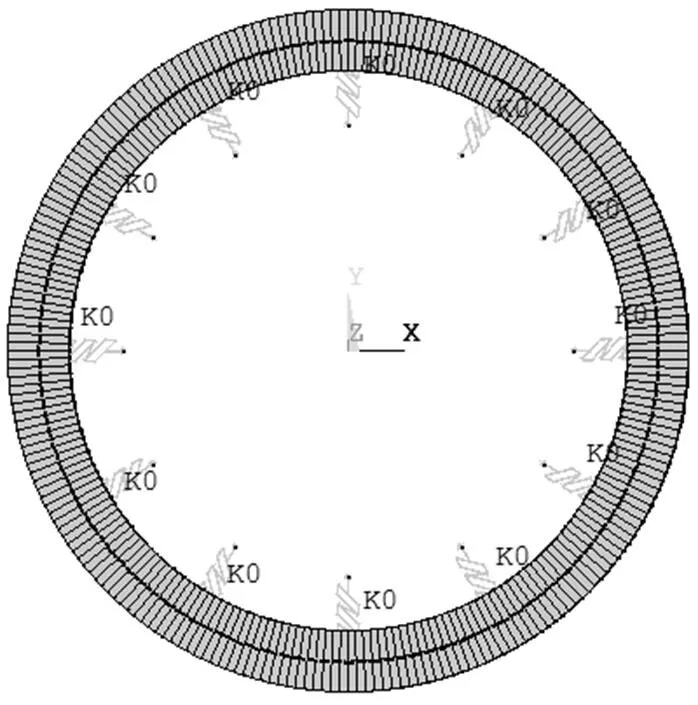
图6 第32号线饼多跨模型
1)对绕组进行分析时认为绕组是同心式的。
3)假设绕组上的电磁力是沿着圆周均匀分布的且指向圆心。
4)因变压器撑条的一端是固定在纸筒中的,另一端与线饼相连接,故combin14弹簧单元靠近纸筒一端为全约束,而另一端为UY、UZ位移约束和ROTX、ROTY转角约束;线饼上其他的节点则为UZ位移约束,ROTX、ROTY转角约束。
对该多跨模型上的每个节点施加指向圆心的单元载荷,利用有限元软件的结构动力学分析可以计算出该线饼的临界屈曲值为68.721kN/m,则第32号线饼的安全系数为1.897,表明受到电磁力最大的第32号线饼在短路时仍是稳定的,还未发生失稳状态。
通过ANSYS的/post1单元可以获得线性屈曲分析的位移云图如图7所示,该线饼的临界载荷值为68.721kN/m,此时的的辐向位移值达最大,为6.93mm,若变形量超出此范围就会导致变压器绕组的失稳甚至匝间绝缘破坏等事故的发生,影响电力系统正常运行。

图7 第32号线饼线性屈曲分析位移云图
考虑到实际工程情况,需要对绕组进行非线性屈曲分析,该分析方法是将线性屈曲分析的结果引入缺陷考虑进去,再综合绕组的材料非线性因素。当32号线饼所受的电磁力为36.22kN/m时的非线性屈曲分析的位移云图如图8所示。从中可知变压器的辐向最大变形量为0.949mm,该值较线性屈曲分析小了5.981mm。通过对辐向位移的校验发现,非线性屈曲分析更接近于工程实际。

图8 第32号线饼非线性屈曲分析位移云图
3 绕组的冲击累积效应
3.1 弹塑性力学理论基础
根据全量理论的条件可知:
平均应力与平均应变的关系为

应力的主方向与应变的主方向是一致的,并且在加载的整个过程中方向始终未发生改变,所以有

由此可推出
(16)
式中,S为应力偏张量;为可变的刚度系数;e为应变偏张量。
应力强度与应变强度的函数关系为
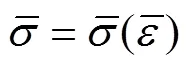
则全量形式的弹塑性本构关系为
(18)
将其改写为矩阵的形式,该应力-应变的形式为
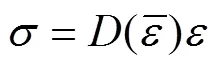
此时,弹塑性平衡边值方程若改用矩阵形式时:
平衡方程为

几何方程为
(21)
物理方程为
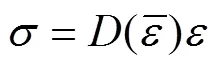
边界条件为
位移边界条件=0 (23)
应力边界条件为

再根据Mises屈服条件,可以判断是否进入塑性阶段。
3.2 中压绕组的冲击累积效应
极短的短路时间内产生较大的电磁力作用在绕组上,可认为是冲击载荷,这种冲击会将很高的能量以冲击波的形式作用在整个绕组上;并且这种冲击会以极大的形变速度来影响绕组的力学性能。
将线饼的材料特性考虑进去以后,绕组的多次冲击会使得材料从弹性阶段进入塑性阶段,进而发生不可恢复的变形,且这种塑性变形不具有连续性特征。
累积效应的分析模型仍按照图6所示,取内法线的方向为正方向。每次施加于绕组上的冲击力如图5所示。选取变压器模型上的一个节点进行分析。现对模型进行一次冲击,得到的位移量()随时间的关系曲线如图9所示,可以发现绕组只发生的弹性形变。

图9 一次冲击时绕组的位移量
累积15次短路冲击后的位移量随时间变化的曲线如图10所示,此时绕组产生了极大形变,材料已经由弹性阶段进入了不可恢复的塑性阶段。

图10 15次冲击时绕组的位移量
图11所示的是连续30次短路冲击后的位移变化量,此时绕组的最大移量已经达到8.3mm,已经大大超出了绕组材料的临界拉伸应力值,即超出绕组的的辐向稳定值,会发生失稳,此时绕组的匝间绝缘等会受到严重的破坏,运行状况会进一步的恶化,造成变压器的绕组还未到达临界屈曲值时已经发生失稳。

图11 30次冲击时绕组的位移量
4 结果验证
根据省电科院等对变压器进行解体检查发现,该主变A、B相中压侧绕组出现较为明显变形,其中以A相变形最为严重,B相也存在多处变形,而其他绕组未见明显变形。其中B相绕组的变形如图12所示。可以发现中压侧绕组的变形主要集中在绕组的中部附近。图中的切向扭曲变形主要是由于绕组螺旋上升的倾角在圆周方向的分量和辐向漏磁场的共同作用下形成的。

图12 中压绕组变形图
该报告还显示从2008年1月开始,该主变就发生了多次35kV侧馈线短路事件。仅2010年,接在该主变中压侧的东溪、东前、东川三条35kV线路,就发生18次过流Ⅰ段跳闸,未见其他事故报告。可以发现该主变的辐向失稳主要是由多次短路冲击引起绕组的累积变形造成的。在实际中引起该主变失稳的短路冲击的次数与上述理论分析基本相吻合,故验证了上述理论的正确性。
5 结论
1)绕组的每个线饼所受的电磁力随时间的变化趋势与短路电流相仿。在本文中,它们均在=0.01s处达峰值,随后随时间逐步衰减至某一稳定值。
2)通过有限元仿真发现变压器绕组中部的轴向漏磁明显大于端部,造成中部线饼的电磁力明显大于端部,此结果与理论相一致。
3)绕组的非线性屈曲更贴近于实际工程,准确度更高。
绕组经受多次短路冲击时,绕组的材料属性会从弹性阶段变化为塑性阶段,造成不可恢复的形变直至辐向失稳,所以短路冲击具有累计效应。
[1] 刘兴平, 陈民铀. 一种配电变压器绕组变形故障的在线监测新方法[J]. 电力系统保护与控制, 2013(12): 20-26.
[2] 刘效真, 高占岭, 李秀国, 等. 一起变压器绕组变形故障的分析与判断[J]. 电气技术, 2015, 16(8): 92-94.
[3] 刘航宇, 刘念, 蒲丽娟,等. 基于ANSYS的高压大截面电缆金具短路电动力和机械应力分析[J]. 电工技术学报, 2016(5): 170-176.
[4] Bakshi A, Kulkarni S V. Analysis of buckling strength of inner windings in transformers under radial Short- Circuit forces[J]. IEEE Transactions on Power Delivery, 2014, 29(1): 241-245.
[5] Ahn H M, Lee J Y, Kim J K, et al. Finite-Element analysis of Short-Circuit electromagnetic force in power transformer[J]. Industry Applications, IEEE Transactions on, 2011, 47(3): 1267-1272.
[6] 王录亮. 电力变压器绕组短路力计算[D]. 哈尔滨: 哈尔滨理工大学, 2012.
[7] 刘军, 张安红. 电力变压器绕组短路动稳定能力的仿真和评估[J]. 变压器, 2012, 49(6): 14-25.
[8] 白永刚, 刘文里, 吴明君, 等. 自耦变压器串联绕组辐向稳定性分析[J]. 黑龙江电力, 2014, 36(1): 42-45.
[9] 姜山. 电力变压器绕组变形的受力分析[D]. 北京: 华北电力大学, 2012.
[10] 周国伟, 刘文州, 罗阀, 等. 基于虚功原理的变压器轴向电动力测算[J]. 变压器, 2015(2): 1-5.
[11] 郝文化, 肖新标. ANSYS7.0实例分析与应用[M]. 北京: 清华大学出版社, 2004.
[12] Kojima H, Miyata H, Shida S, et al. Buckling strength analysis of large power transformer windings subjected to electromagnetic force under short circuit[J]. IEEE Transactions on Power Apparatus&Systems, 1980, PAS-99(3): 1288-1297.
[13] 徐健学, 徐子宏. 弹性支持扁拱动力稳定性分析和变压器内线圈短路动稳定分析[J]. 应用力学学报, 1992(2): 14-25.
[14] 李健. 大容量变压器绕组稳定性及油箱强度研究[D]. 沈阳: 沈阳工业大学, 2012: 5-35.
Research on Radial Stability of Power Transformer
Hu Zhongping1Liao Fuwang1,2Lan Sheng1
(1. College of Electrical Engineering and Automation Fuzhou University, Fuzhou 350108;2. Electric Power Research Institute of Fujian Electric Power Co., Ltd, Fuzhou 350007)
With the increase of the power system capacity, it is necessary for the transformer windings to carry on the buckling and elastic-plastic mechanics analysis, because electrodynamic force that the short-circuit trouble produces can cause deformation of transformer windings and the problem of the stability in radial direction. The buckling and elastic-plastic mechanics of transformer windings were analyzed by ANSYS software in the medium voltage winding of the three-phase short circuit in this paper. The radial stability coefficient of the medium voltage winding was obtained by the model of 50MVA main transformer of three windings. This method has certain reference value for analysis of transformer short-circuit impact, and also has some reference significance for the design and fabrication of large transformers according to the verified accident examples.
power transformer; field-circuit couple; the electromagnetic force; buckling analysis; elastic-plastic mechanics
福建省自然基金资助项目(2015J01194)
胡忠平(1988-),男,安徽省桐城市人,硕士研究生,主要研究方向:变压器绕组稳定性的研究。
