多类型噪声中的独立成分分离算法
2017-10-13冯平兴
冯平兴,魏 平
多类型噪声中的独立成分分离算法
冯平兴,魏 平
(电子科技大学电子工程学院 成都 611731)
该文将一般的噪声独立成分分离算法扩展到多类型噪声混合环境。为了识别观测数据中的多类型噪声成份,利用基于S估计原理的非多项式函数,对观测数据进行投影分析,给出脉冲噪声阈值估计及噪声去除和重构信号方法。此外,结合独立噪声分析算法,提出了一种针对多类型噪声的快速独立成份分离算法。该算法解决了传统噪声ICA在多类型噪声环境,特别是脉冲噪声时的失效性问题,极大地提高了噪声ICA算法的分离性能。仿真分析验证了该方法的有效性。
独立成分分析; 多维信号处理; 噪声; 噪声算法
盲源分离(blind signal separation, BSS)是信号处理技术中新发展起来的方法。与传统的信号处理技术相比,具有很多优良的特点。它仅利用所观测到的数据,用统计的方法对信号进行分离。由于对观测信号不需要获得先验知识,所以被广泛用于定位跟踪、多输入多输出、数字水印等领域[1-9]。传统的噪声独立成份分析算法中常用的去除噪声算法主要有:偏差去除技术、极大似然估计、最大后验估计和稀疏码收缩等方法。
文献[5-6]提出了一种基于偏差消除方法用于消除观测数据中的高斯噪声。极大似然估计主要用于对混合矩阵的估计[7],然而该方法随着信号维数的增加,其计算量会迅速增长,极大地降低了算法的效率。极大后验估计和稀疏码收缩法[8-11]除了计算量的问题外还对数据的模型做了精确的假设,因而上述方法难以满足多类型噪声的环境。本文将传统的噪声独立成分分离方法推广到多类型噪声环境,利用该方法在不增加计算量的基础上可以将混有多种噪声的独立源信号分离出来。
1 噪声独立成分混合模型
1.1 独立成分的混合
无噪声独立成分混合模型是基于信号源之间相互独立且为非高斯的假设,估计信号与源信号的关系可以表示为:

(2)

1.2 噪声混合模型
当噪声混入源信号后,相应的观测信号可以表示为:

或
(5)

利用简单的数学关系可以得到此时被估计噪声的另一种表示形式:。因而式(5)可以重写为:[5-6]。一般地,如果噪声成分分别加载到源信号之上,又或者噪声成分的协方差具有特定的形式,那么混合信号的估计就可以用经典的ICA分离算法得到。
然而,当噪声的类型为多种,特别是在源信号中混有冲击噪声和高斯噪声时,那么式(4)和式(5)可表示为:

和
(8)
在这种情况下,脉冲噪声会对经典的ICA分离算法有显著的影响,使得估计的分离矩阵精度难以保证,甚至失去原有的分离性能,因而对混合噪声中的脉冲成分分析是必要的。
2 脉冲成分分析
2.1 非多项式函数
由于对观测数据进行白化处理会使得ICA问题变得简单,因此可以对噪声成分进行白化投影处理。

因而,对观测到的噪声成分,白化处理可以表示为:
(10)
为了分析观测数据中的脉冲成分,本文提出利用基于S估计原理,构造合适的非多项式函数对观测数据进行投影处理,定义为:
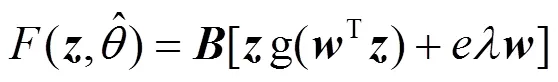
(12)
根据S估计的理论基础,并结合仿真试验,本文给出了两个用于数据投影的非多项式函数:
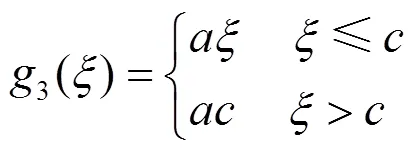
(14)
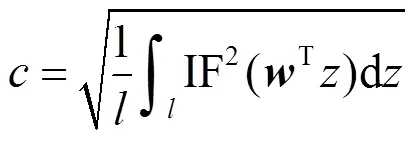
(16)
2.2 脉冲噪声的消除
由于阈值是随观测数据而变化,实验表明观测数据中如果脉冲噪声不太严重,又或者脉冲噪声为稀疏型分布的情况下,式(16)具有良好的检验性能。由式(16)的结果仅能判断数据脉冲噪声的存在性,为了消除脉冲噪声对分离性能的影响,本文给出了去除脉冲噪声并重构数据的方法为:
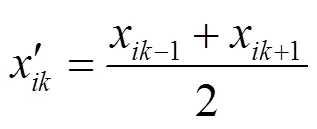
(18)
实验表明,式(17)对于平稳型数据具有良好的处理效果,而式(18)处理超高斯型数据中的脉冲噪声问题时效果显著。式(17)和式(18)是基于观测数据含有脉冲噪声而提出的,当数据中没有脉冲噪声时,上述处理方法仍然有效。由于进行了平均运算,其作用机理相当于滤波,因此不会对源数据有实质的影响。
2.3 多类型噪声中的分离算法
通过上述分析,可以得到关于多类型噪声环境中的独立成分分析的分离算法:
1) 对观测的噪声数据中心化处理使其均值为0;
2) 利用式(10)对数据进行白化处理;
4) 利用合适的非多项式函数,如式(13)、式(14)对观测数据进行投影,并计算阈值;
6) 利用式(17)或式(18)去除脉冲噪声并重构数据;
7) 利用噪声ICA分离算法迭代:
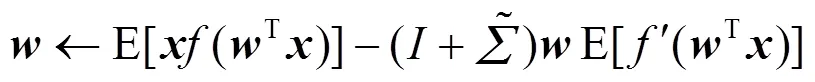
9) 如果仍未收敛,则返回步骤7)。
3 仿真分析
为了分析算法的有效性,本文利用混有高斯白噪声和脉冲噪声的超高斯和次高斯信号进行仿真分析。观测信号由式(7)或者式(8)给出。为了便于比较,所有的实验中高斯噪声协方差矩阵设定为,混合的脉冲噪声为:

此外,为公平起见,用于实验的源信号、参数设置一致。为了评价算法的分离性能,本文引入了Amari指数[14]进行分析,其计算可以表示为:
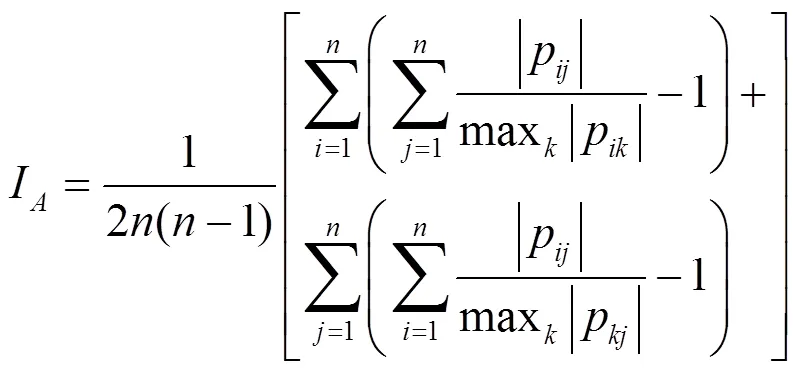
首先,本文对传统的噪声ICA算法和本文提出的多类型噪声ICA算法在源信号混有高斯白噪声和脉冲噪声的情况下进行比较。3种用于仿真的源信号为三角波信号、由多种不同频率正弦波叠加的信号、正弦信号,其幅值分别为1.8、2、2,图2和图3分别给出了分离信号的结果。
从分离结果可以看出,当混入脉冲噪声成分时,传统的噪声ICA算法失去了应有的性能,此时虽然算法整体上仍然具有收敛性,然而其分离出的信号已经失去意义。相比之下,由图3可以看出,本文提出的算法能够成功分离出相应的源信号。

图4显示了两种算法在多类型噪声的环境中随信号样本数量增长的分离性能结果。
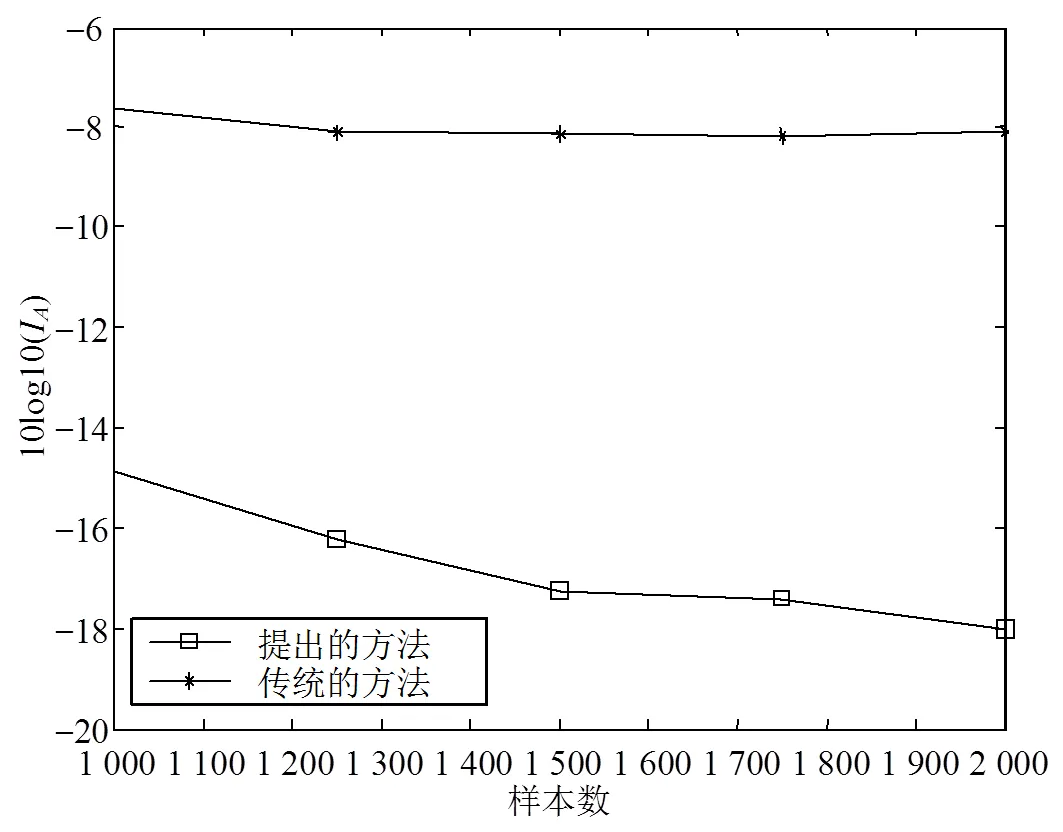
图4 不同样本长度下的分离性能
仿真结果显示,本文提出的算法随着样本数量增加,分离性能提高;然而,由于未考虑到脉冲噪声的影响,即使增加信号样本数量,传统的噪声ICA算法仍然无法成功分离源信号。
图5给出了两种算法在不同信噪比下的分离性能。
可以看出,本文的算法性能随信噪比的增加而改善。虽然传统的噪声ICA算法的性能随信噪比的增加而局部改善,然而由于脉冲噪声影响,使得估计矩阵的精度大幅度降低,甚至导致算法无法收敛,即使收敛,分离的结果仍不能满足分离信号的要求。
4 结束语
本文提出了一种用于在多类型噪声环境中的独立成分分离算法。利用S估计原理给出了用于分析脉冲噪声的非多项式函数,并提出了脉冲噪声的阈值估计及脉冲噪声的去处和重构信号的方法。仿真结果表明,本文提出的算法能够在多类型噪声中实现对独立成分的分离,并显示出良好的性能。
[1] BREUER L, DAMMERS J, ROBERTS T P, et al, A constrained ICA approach for real-time cardiac artifact rejection in magneto encephalography[J]. IEEE Transactions on Biomedical Engineering, 2014, 61(2): 405-414.
[2] WANG Xiao-feng, ZHANG Xiao-Ping. An ICA mixture hidden conditional random field model for video event classification[J]. IEEE Transactions on Signal Processing, 2013, 61(24): 46-59.
[3] NAFTA A, JOHANNISSON P, SHTAIF M. Blind equalization in optical communications using independent component analysis[J]. Journal of Lightwave Technology, 2013, 31(12): 2043-2049.
[4] HYVARINEN A. Fast independent component analysis with noise data using Gaussian moments[C]//Proc Int Symp on Circuits and Systems. Orlando, Florida, USA: [s.n.], 1999.
[5] HYVARINEN A. Gaussian moments for noisy independent component analysis[J]. IEEE Signal Processing Letters, 1999, 6(6): 145-147.
[6] MOULINES E, CARDOSO J, GASSIAT E. Maximum likelihood for blind separation and deconvolution of noisy signals using mixtures models[C]//Proc IEEE Int Conf on Acoustics, Speech and Signal Processing. Munich, Germany: IEEE, 1997.
[7] KOIVUNEN V, ENESCU M, OJA E. A adaptive algorithm for blind separation from noisy time varying mixtures[J]. Neural Computation, 2001, 13(10): 2339-2357.
[8] KOIVUNEN V, OJA E. Predictor-corrector structure for real time blind separation from the noisy mixtures[C]//Proc Int Workshop on Independent component Analysis and Signal Separation (ICA’99). Aussois, France: [s.n.], 1999.
[9] HYVARINEN A. Sparse code shrinkage: Denoising of nongaussian data by maximum likelihood estimation[J]. Neural Computation, 1999, 11(7): 1739-1768.
[10] HAYKIN S, KOSKO B. IIntelligent signal processing[M]. New York, USA: Wiley-IEEE Press, 2009.
[11] HYVARINEN A, KARHUNEN J, OJA E. Independent component analysis[M]. New York, USA: Jhon Wiley & Sons, 2001.
[12] ROUSSEEUW P J, LEROY A M. Robust regression and outlier detection[J]. Wiley-Interscience, 1987, 31(2): 260-261.
[13] AMARI S, CICHOCKI A, YANG H H. A new learning algorithm for blind signal separation[C]//Advances in Neural Information Processing Systems. Denver, USA: NIPS, 1995.
编 辑 税 红
Algorithm of Independent Component Analysis for Multi-Types Noise Moments
FENG Ping-xing and WEIPing
(School of Electronic Engineering, University of Electronic Science and Technology of China Chengdu 611731)
The performance of fast fixed-point algorithm of independent component analysis (ICA) is influenced by noise significantly. However, the method of noisy ICA proposed by Hyvärinen did not discuss the impulsive noise. In this study, we extend the algorithm proposed by Hyvärinen for noisy ICA to the more general situation in which the signals are observed in the presence of Gaussian and impulsive noise. We use the non-polynomial function to analyze the impulsive noise, which is to guarantee the impulsive noise can be distinguished from the observed data. Furthermore, combined with the noisy ICA method, a modification to the algorithm for multi-noise is introduced. The proposed technique improves the performance of Hyvärinen’s algorithm for cases where the observed signals contain Gaussian and impulsive noise. We also perform simulations to demonstrate the effectiveness of the proposed method.
independent component analysis; multidimensional signal processing; noise; noisy algorithm
TN97
A
10.3969/j.issn.1001-0548.2017.02.006
2015-06-10;
2015-10-12
国家自然科学基金(11176005)
冯平兴(1981-),男,博士,主要从事信号处理、盲源分离等方面的研究.
