基于双阈值AdaBoost算法的4-CBA含量软测量建模
2017-10-13刘瑞兰刘树云戎舟江兵庞宗强
刘瑞兰,刘树云,戎舟,江兵,庞宗强
基于双阈值AdaBoost算法的4-CBA含量软测量建模
刘瑞兰,刘树云,戎舟,江兵,庞宗强
(南京邮电大学自动化学院,江苏南京 210003)
针对PX氧化过程中4-CBA含量无法在线测量的问题,提出了一种基于双阈值更新样本权重的AdaBoost算法,该算法以BP神经网络作为弱学习器,采用轮盘赌方法根据样本权重在训练样本集中选择部分样本训练弱学习器,采用上一轮弱学习器的训练相对误差绝对值来更新所有训练样本的权重,在此基础上,用双阈值对样本误差范围进行划分,然后用不同的权重因子与原来的样本权值相乘实现样本权值的二次更新。该过程降低了含有大误差的样本的权值,增加了较大误差的样本的权值,从而减小了在下一轮训练过程中选到异常样本的概率。分别采用5种不同的方法并用实测的工业数据建立了4-CBA含量软测量模型,仿真结果表明用提出的改进AdaBoost算法建立的4-CBA含量软测量模型,其预测误差小于其他方法建立的模型误差。
AdaBoost算法;软测量;双阈值;异常样本;4-CBA含量;轮盘赌方法
引 言
精对苯二甲酸(purified terephthalic acid,PTA)是制造聚酯纤维和化工生产中重要的有机原料。对羧基苯甲醛(4-carboxy-benzaldchydc,4-CBA)是PTA生产过程中对二甲苯(paraxylene,PX)氧化反应的副产物,为保证产品纯度一般工业要求其含量为2.0~3.5 g·kg-1[1]。但PTA生产过程中涉及多元热力学平衡,工艺流程复杂,按照常规方法难以精确测量并控制4-CBA含量。而4-CBA含量是反应过程中主要产品质量的重要指标,当4-CBA含量不在要求范围时会严重影响产品的质量,本文将采用软测量技术来解决4-CBA含量不能在线测量的问题。
软测量技术的核心是建立软测量模型。目前,有关4-CBA含量的软测量建模方法主要分为机理建模方法[2-5]和基于数据驱动的建模方法[6-13]。文献[2]提出了一个基于实验小试结果的PX氧化反应机理模型,并对反应温度、催化剂浓度、停留时间、反应器尾氧浓度对反应物浓度的影响进行了研究。文献[3]在文献[2]的基础上,对模型中的某些参数设置装置因数,并提出了改进的LM (Levenberg-Marquardt)阻尼非线性最小二乘算法和工厂实测数据来辨识装置因数。由于非线性最小二乘法对初始值比较敏感,文献[4]提出了用支持向量机提取特征样本、采用粒子群算法辨识装置因数的4-CBA含量机理软测量模型,避免了传统方法对初始点和样本的依赖。文献[5]采用简化的机理模型,根据4-CBA含量和氧化反应器进料流量与第一结晶器空气流量的非线性函数关系,结合优生优选进化算法对模型的参数进行估计。文献[6]采用3层BP人工神经网络并结合LM学习规则建立了4-CBA含量的软测量模型;文献[7]利用贝叶斯方法,结合多项式线性基函数,建立了4-CBA含量的软测量模型;文献[8-9]提出用模糊神经网络方法建立了4-CBA含量的软测量模型;文献[10]和[11]都采用最小二乘支持向量机方法建立4-CBA含量的软测量模型,并分别用参数的自动调整方式和稀疏化的方式提高模型的泛化性能;文献[12]和[13]分别采用模糊支持向量机和偏最小二乘结合前向神经网络方法建立4-CBA含量的软测量模型。由于机理模型本身包含了过程本质的信息,因此模型的泛化性能较好。但是对于复杂的过程,机理模型建立比较困难。基于数据驱动的方法建立软测量模型则需要大量高质量的训练样本和合适的算法,基于经验风险最小化的BP神经网络方法和模糊神经网络方法可能会出现过拟合现象。
应用于软测量建模的训练样本都来自工厂的实测过程数据和分析数据,样本不可避免会存在误差,有些甚至含有粗大误差,含有粗大误差的样本会严重影响模型准确度。针对这一问题,本文提出了双阈值AdaBoost(adaptive Boosting)算法,该算法以一个隐含层、隐含层节点数为2的简单的BP神经网络作为弱学习器,采用轮盘赌方法根据样本权重在总的训练样本集中选择部分样本训练弱学习器,并用弱学习器的相对训练误差的绝对值来更新每个训练样本的权重。在此基础上,缩小含有粗大误差的训练样本权重,放大一些具有较大随机误差的训练样本权重,这样可以防止在第2轮以后的弱学习器学习中每次都选中具有粗大误差的训练样本。最后将本文提出的方法建立了PX 氧化过程中4-CBA含量的软测量模型,比较了不同方法建立的软测量模型的训练精度和预测精度。
1 BPNN-AdaBoost 回归算法简介
AdaBoost.R算法是由Freund等[14]提出的应用到回归问题中的方法,Drucker[15]在AdaBoost.R的基础上提出了改进的AdaBoost.R2算法验证了回归问题的适用性。2004年,Solomatine等[16]在AdaBoost.R算法的基础上通过设置阈值提出了AdaBoost.RT算法用于回归预测。Baumann等[17]通过设定阈值限定分类器来排除误差较大的分类器,在训练时间上作了改进,提出SEAdaBoost算法;袁双等[18]结合PCA降维方法来提高AdaBoost算法的训练速度;查翔等[19]提出了一种以均方根相对误差为衡量标准的自适应调整阈值的方法,提高了预测精度题;Zhang等[20]以每个弱学习器的统计误差来自动调节阈值,提高了算法的精度和速度;胡国胜[21]将加权的支持向量机作为弱学习器应用于电力负荷预测,提高了预测精度;刘庆华等[22]在高速公路交通事件检测时选用遗传算法优化BP神经网络弱学习器,降低了误报率。
AdaBoost算法原理是将多个弱学习器多次训练并组合成强学习器。强学习器预测精度高于单一弱学习器[23]。BPNN-AdaBoost算法是将BP神经网络作为弱学习器,反复训练得到一组弱学习器,最后将这组弱学习器组合得到强学习器,其训练步骤如下[24-25]。
(1)确定输入输出样本,初始化BP神经网络参数,并设置迭代次数。给定一组训练样本(,),其中∈R,∈,为输入,为输出。
(2)样本预处理。将输入输出数据归一化。
(3)初始化训练样本的权重。给每个训练样本设置初始权重1=1,并给每个训练样本指定一个初始概率

其中,为训练样本个数。
(4)训练弱学习器。将单一BP神经网络作为弱学习器进行训练,计算弱学习器的相对误差绝对值

其中,f(x)为第个弱学习器在训练输入x时的估计值,y为训练样本的实际值。
(5)计算第个弱学习器的训练平均损失函数值
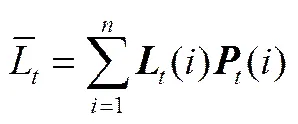
其中
(4)
(6)计算弱学习器权重系数,依据弱学习器平均损失函数计算弱学习器权值,计算公式为
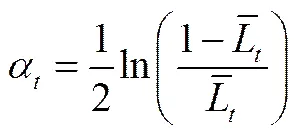
从式(2)、式(3)和式(5)可以看出,所有样本的相对误差绝对值越小,弱学习器平均损失函数也越小,弱学习器权值越大。
(7)更新样本权重和概率。

(7)
(8)判断循环次数是否达到次,若达到则结束循环向下执行,否则返回步骤(4)。
(9)合成强学习器,训练结束后得到一组弱学习器,将其组合成强学习器,组合算式为
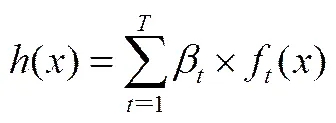
其中
2 双阈值BPNN_AdaBoost算法
2.1 弱学习器训练样本的选择
本文提出了如下的方法选择BP神经网络弱学习器的训练样本,当=1时,用全部训练样本集中的样本训练弱学习器。当>1时,依据每个样本的概率()采用轮盘赌的方法对样本进行重采样。轮盘赌方法是由Holland[26]提出用于遗传算法中按概率选择个体的随机方法,该方法类似于赌博游戏中的赌轮盘,群体中的每个个体的适应度按比例转化为选中概率,根据该概率将轮盘分成与个体数目相同的扇区,扇区的大小与概率呈正比。旋转这个轮盘,直到轮盘停止时,看指针停止在哪一块上,就选中与它对应的那个个体,个体概率越大,被选中的机会越大。这种方法的好处是在迭代过程中训练样本不一样。但是随着迭代的进行,误差绝对值大的样本对应的()也越大,被抽取作为下一轮训练样本的概率越大,最后每次都有可能选中这些误差大的样本,导致所有的弱学习器近似相同。
2.2 双阈值更新样本权重
本文对式(6)更新样本权重公式进行了如下改进
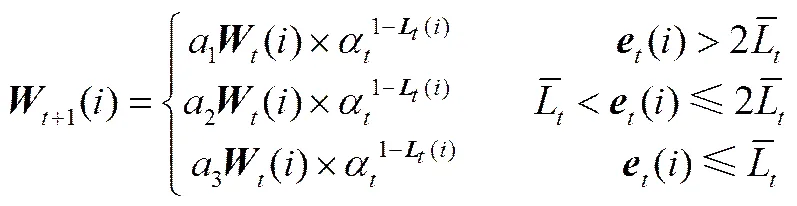
其中1,2,3分别为不同的权重调整因子,为更新样本的权重,1、2取值在1附近,且2>3=1>1。当训练样本的误差()大于2倍相对误差绝对值均值时,这部分样本可以看成是具有粗大误差的样本,通过乘一个小于1的调整因子,缩小样本权重,减小该样本在下一轮训练弱学习器时被选中的概率。当训练样本的误差()位于1倍和2倍相对误差绝对值均值之间时,这部分样本可以看成是具有较大随机误差的样本,通过乘一个大于1的调整因子,放大样本的权重,提高该样本在下一轮训练弱学习器时被选中的概率。值得指出的是,式(9)改变了样本的权重,从而改变了式(7)的概率+1(),但是这种改变有的增加,有的减小,在迭代过程中对平均损失函数值有一定的影响,最终会导致弱学习器的权重不会出现较大的分散度。
3 仿真实例
为了验证提出的双阈值BPNN_AdaBoost算法的有效性,选用通用函数=sin(p)/(p)+作为例子,其中训练输入样本∈[-4,4],为[-0.03,0.03]均匀分布的噪声。训练样本中有5个点加了粗大误差,如图1所示。分别采用本文提出的方法和经典的BPNN_AdaBoost算法进行了仿真实验,其中弱学习器个数为5,弱学习器的隐含层节点数为10,隐含层数为1。
图1显示了两种方法得到的模型的拟合值和预测值与对应的实际值和真实值之间的比较曲线。图2显示了模型输出值与真实值之间的相对误差比较。从图中可以看出,双阈值方法得到的模型更能逼近函数的真实值。
4 应用实例
4.1 PX氧化过程简介
PX氧化过程[27-29]是在反应温度为190℃左右,压力为1.258 MPa,在醋酸钴、醋酸锰等催化剂和溴化物促进剂作用下以醋酸为溶剂,用空气中的氧气将PX氧化为TA (terephthalic acid,对苯二甲酸),并将TA溶于水后经过逐级降温,再固液分离干燥后得到PTA (purified terephthalic acid,精对苯二甲酸)的过程。PX氧化反应过程中会出现3种中间产物:对甲基苯甲醛(-tolualdehyde, TALD)、对甲基苯甲酸(-toluic acid, PT)和4-CBA。而4-CBA是氧化反应的主要副产物,是衡量产品的重要指标。
4-CBA含量无法用常规的传感器在线测量,而是通过实验室分析化验出来,化验时间比较长;同时由于化验成本较高,其采样间隔较长,比如某工厂对4-CBA含量的采样周期为8 h,每天固定在0点,8点和16点采样,因此一天最多只有3个滞后数小时的4-CBA含量的分析值。
4.2 软测量模型输入变量的选择
影响4-CBA含量的因素较多,综合文献[4,11,30]选择氧化反应器物料进料流量、氧化反应器催化剂浓度、氧化反应器溶剂、氧化反应器液位、氧化反应器温度、氧化反应器尾氧含量、第一结晶器温度、第一结晶器尾氧含量、第三冷凝器排出水量、第四冷凝器排出水量、反应生成的二氧化碳含量和反应生成的一氧化碳含量共12个过程变量作为软测量模型的输入变量。
4.3 工业数据仿真结果
本文采用的数据来源于某化工厂,共收集了196组样本,样本按时间顺序排列,取前面120组样本作为训练总样本,后面76组样本作为验证样本。
采用BP神经网络作为双阈值AdaBoost算法的弱学习器,所有神经网络弱学习器只有一个隐含层,输入层节点个数为12,为了减少弱学习器的规模,选择隐含层节点个数为2,弱学习器的个数为5。弱学习器的初始值均随机赋值,采用轮盘赌方法根据样本权重在训练样本集中选择80%以上的样本训练弱学习器。1和2根据经验分别选为0.78和1.1。
本文采用相对误差绝对值的平均值作为模型的性能指标,具体计算公式为

式中,y为实际值,y′为估计值,是样本个数。
为了验证本文提出的双阈值BPNN_AdaBoost算法的性能,分别比较了双阈值非轮盘赌BPNN_AdaBoost算法模型、非双阈值轮盘赌BPNN_AdaBoost算法模型、非双阈值非轮盘赌的BPNN_AdaBoost算法模型和单一的BP神经网络模型的性能,其中非轮盘赌表示所有训练样本都参与弱学习器的学习。单一BP神经网络模型结构为输入层节点数12,隐含层节点数10。
在弱学习器的学习过程中,第3、第6、第103和第105号训练样本的相对误差绝对值均大于2倍的平均相对误差。在没有使用双阈值改变样本权重的BPNN_AdaBoost算法中,每次都被选中,而在双阈值改变样本权重的BPNN_AdaBoost算法中,只有1次被选中。
表1给出了不同方法的相对误差绝对值的平均值,从表中可以看出,本文提出的双阈值结合轮盘赌选择训练样本的BPNN_AdaBoost算法建立的软测量模型的预测误差(PE)最小,训练误差(TE)最大,但是两者数值较接近。这是因为双阈值法减小了粗大样本的权重,在使用轮盘赌重采样时,这部分样本被选中的概率变小,在5个弱学习器中,只有2个弱学习器使用了含有粗大误差的样本,由于含有粗差的样本只用于少量的弱学习器的学习,使得最终模型的预测误差较小,没有出现过拟合现象。从表1中还可以看出,轮盘赌方式选择训练样本时训练误差都比较大,这是因为采用轮盘赌的方式选择训练样本时,实际上是在给定的120组训练样本中依据每个样本的权值选择80%的样本作为每轮弱学习器的训练样本,没有选中的样本不参与弱学习器的训练,也就是说采用轮盘赌的方法实质上是将总的训练样本分成了训练样本子集和测试样本子集,因此总的训练误差包含训练样本子集的拟合误差和测试样本子集的测试误差,导致总的训练误差比较大。
从表1可以看出采用轮盘赌的方式训练的软测量模型预测误差相比而言较小。虽然从模型规模上看,本文由5个BP弱学习器组成的BPNN_AdaBoost强学习器软测量模型(每个弱学习器结构为12-2-1)和一个12-10-1的单一BP神经网络软测量模型一样,但是本文提出的方法建立的软测量模型的预测效果是最好的。

表1 不同方法建立的4-CBA软测量模型结果比较
BPNN_AdaBoost也可以看成是一种串行训练BP神经网络的方法,在网络规模相同的情况下,串行方法训练时间长,但是模型的预测效果与单一的BP神经网络相比要好得多。图3分别显示了本文提出的双阈值方法建立的4-CBA含量软测量模型和单一BP神经网络软测量模型的拟合值、预测值和对应的真实值的比较曲线。
5 结 论
本文以小规模BP神经网络为弱学习器,采用双阈值BPNN_AdaBoost算法,通过增加调整因子的方式二次更新训练样本的权值,使得模型训练不再仅专注误差大的样本。采用轮盘赌方法在训练样本集中选择部分样本训练弱学习器,增加了弱学习器的多样性。最后用本文提出的方法建立了4-CBA含量的软测量模型,用工业数据仿真结果表明,用本文提出的方法与单一的BP神经网络模型相比,在不增加模型规模的情况下,预测效果提高了几乎一个百分点。
References
[1] 冒永生, 杨开香, 王丽军. PTA装置氧化过程实时优化与先进控制[J]. 化工自动化及仪表, 2012, 39(9): 1128-1132. MAO Y S, YANG K X, WANG L J. Real-time optimization and advanced control for pta oxidation process[J]. Control & Instruments in Chemical Industry, 2012, 39(9): 1128-1132.
[2] 王丽军. PX氧化动力学研究及氧化反应器模拟[D]. 杭州: 浙江大学, 2001. WANG L J. Studies on the kinetics of-xylene oxidation oxidation and the reactor simulation[D]. Hangzhou: Zhejiang University, 2001.
[3] 牟盛静. 石化工业过程建模与优化若干问题研究[D]. 杭州: 浙江大学, 2004. MOU S J. The studies of process modeling and optimization in petrochemical industry[D]Hangzhou: Zhejiang University, 2004.
[4] 刘瑞兰, 牟盛静, 苏宏业, 等. 基于支持向量机和粒子群算法的软测量建模[J]. 控制理论与应用, 2006, 23(6): 895-900. LIU R L, MOU S J, SU H Y,Modeling soft sensor based on support vector machine and particle swarm optimization algorithms[J]. Control Theory and Applications, 2006, 23(6): 895-900
[5] 颜学峰, 余娟, 钱锋. 基于自适应偏最小二乘回归的初顶石脑油干点软测量[J]. 化工学报, 2005, 56(8): 1151-1156. YANG X F, YU J, QIAN F. An evolution algorithm with select-best and prepotency operator and parameter estimation of 4-CBA model[J]. Journal of Chemical Industry and Engineering(China), 2005, 56(8): 1151-1156.
[6] 胡永有, 古勇, 苏宏业, 等. 基于BPANN的4-CBA软测量模型研究[J]. 仪器仪表学报, 2003, 24(3): 226-230. HU Y Y, GU Y, SU H Y,The research of 4-CBA soft- sensor model based on BPANN[J]. Chinese Journal of Scientific Instruments, 2003, 24(3): 226-230.
[7] 陈渭泉, 刘瑞兰, 牟盛静, 等. 基于贝叶斯方法的4-CBA含量的软测量研究[J]. 化工自动化及仪表, 2003, 30(5): 49-51. CHEN W Q, LIU R L, MOU S J,The research on soft sensor of the concentration of 4-CBA based on Bayesian approach[J]. Control & Instruments in Chemical Industry, 2003, 30(5): 49-51.
[8] LIU R L, SU H Y, MOU S J,. Fuzzy neural network model of 4-CBA concentration for industrial PTA oxidation process[J]. Chinese Journal of Chemical Engineering, 2004, 12(2): 234-239.
[9] DU W L, QIAN F, LIU M D,. 4-CBA soft sensor based on fuzzy CMAC neural networks[J]. Chinese Journal of Chemical Engineering, 2005, 13(3): 437-440.
[10] 郑小霞, 钱锋. 基于证据框架的最小二乘支持向量机在精对苯二甲酸生产中的应用[J]. 化工学报, 2006, 57(7): 1612-1616. ZENG X X, QIAN F. Application of least squares support vector machine within evidence framework in PTA process[J]. Journal of Chemical Industry and Engineering(China), 2006, 57(7): 1612- 1616.
[11] 刘瑞兰, 徐艳, 戎舟. 基于稀疏最小二乘支持向量机的软测量建模[J]. 化工学报, 2015, 66(4): 1402-1407. LIU R L, XU Y, RONG Z. Modeling soft sensor based on sparse least square support vector machine[J]. CIESC Journal, 2015, 66(4): 1402-1407.
[12] ZANG Y, SU H Y, LIU R L. Fuzzy support vector regression model of 4-CBA concentration for industrial PTA oxidation process[J]. Chinese Journal of Chemical Engineering, 2005, 13(5): 642-648.
[13] 颜学峰. 基于MLFN-PLSR的PX氧化反应组合建模方法[J]. 化工学报, 2007, 58(1): 149-154. YAN X F. Delvelop-xylene oxidation reaction model based on MLFN_PLSR[J]. Journal of Chemical Industry and Engineering(China), 2007, 58(1): 149-154 .
[14] FREUND Y, SCHAPIRE R E. A decision-theoretic generation of online learning and an application to Boosting[J]. Journal of Computer and System Science, 1997, 55(1): 119-139.
[15] DRUCKER H. Improving regressor using Boosting techniques[C]//Proc. of the 13th Annual Conf. on Computational Learning Theory. San Francisco, 1997: 208-219.
[16] SOLOMATINE D P, SHRESTHA D L. AdaBoost.RT: a boosting algorithm for regression problem[C]//Proc. of the Int. Joint Conf. on Networks. Budapes, 2004: 1163-1168.
[17] BAUMANN F, ERNST K, EHLERS A,. Symmetry enhanced AdaBoost[C]//International Conference on Advances in Visual Computing. Springer-Verlag,2010: 286-295.
[18] 袁双, 吕赐兴. 基于PCA改进的快速AdaBoost算法研究[J]. 科学技术与工程, 2015, 15(29): 62-67. YUAN S, LÜ C X. Fast AdaBoost algorithm based on improved PCA[J]. Science Technology and Engineerring, 2015, 15 (29): 62-67.
[19] 查翔, 倪世宏, 张鹏. 关于AdaBoost.RT集成算法时间序列预测研究[J]. 计算机仿真, 2015, 32(9): 391-395. ZHA X, NI S H, ZHANG P. AdaBoost.RT intergrating prediction of time series based on adaptive and dynamic threshold[J]. Computer Simulation, 2015, 32(9): 391-395.
[20] ZHANG P B, YANG Z X. A novel AdaBoost framework with robust threshold and structural optimization[J]. IEEE Trans Cybem., 2016, (99): 1-13.
[21] 胡国胜. 基于加权支持向量机与AdaBoost集成的预测模型研究[J]. 计算机应用与软件, 2012, 29(12): 280-281. HU G S. Study on forecasting model based on WSVR and AdaBoost[J]. Computer Applications and Software, 2012, 29(12): 280-281.
[22] 刘庆华, 丁文涛, 涂娟娟, 等. 优化BP_AdaBoost算法及其交通事件检测[J]. 同济大学学报(自然科学版), 2015, 43(12): 1829-1833. LIU Q H, DING W T, TU J J,Improved BP_AdaBoost algorithm and its application in traffic incident detection[J]. Journal of Tongji University(Natural Science), 2015, 43(12): 1829-1833.
[23] HU W M, HU W, MAYBNK S. AdaBoost-based algorithm for network intrusion detection[J]. Systems, Man, and Cybernetics, Part B: Cybernetics, IEEE Transactions on, 2008, 238(2): 577-583.
[24] SHRESTHA D L, SOLOMATINE D P. Experiments with AdaBoost. RT, an improved boosting scheme for regression[J]. Neural Computation, 2006, 18(7): 1678-1710.
[25] DEVON K B, SVEN F C. A comparison of AdaBoost algorithms for time series forecast combination[J]. International Journal of Forecasting, 2016, 32(4): 1103-1119.
[26] HOLLAND J H. Adaptation in Natural and Aritificial Systems[M]. Ann. Arbor: University of Michigan Press, 1992: 126-137.
[27] 李希, 谢刚, 华卫琦. PTA技术国产化的主要化学工程问题及其研究思路[J]. 聚酯工业, 2001, 14(1): 1-7. LI X, XIE G, HUA W Q. Key problems and research program for PTA process domestic development[J]. Polyester Industry, 2001, 14(1): 1-7.
[28] 尹云华, 向阳, 刁磊, 等. PTA生产工艺及技术的研究进展[J]. 化工工业与工程技术, 2011, 32(5): 33-39. YIN Y H, XIANG Y, DIAO L,Research progress of PTA production technology[J]. Journal of Chemical Industry &Engineering, 2011, 32(5): 33-39.
[29] 黄浩. 中国PTA行业的发展和现状[J]. 聚酯工业, 2016, 29(1): 1-2. HUANG H. Development and current situation of PTA industry in China[J]. Polyester Industry, 2016, 29(1): 1-2.
[30] 刘瑞兰, 戎舟. 工业PX氧化过程4-CBA含量的软测量[J]. 信息与控制, 2014, 43(3): 339-343. LIU R L, RONG Z. A soft sensor for 4-CBA soncentration in industrial PX oxidation processes[J]. Information and Control, 2014, 43(3): 339-343.
Modeling soft sensor of 4-CBA concentration by AdaBoost algorithm with dual threshold technique
LIU Ruilan, LIU Shuyun, RONG Zhou,JIANG Bing,PANG Zongqiang
(College ofAutomation, Nanjing University of Post & Telecomomunication, Nanjing 210003, Jiangsu, China)
A modified AdaBoost algorithm with updating sample weight by dual threshold technique was proposed to model a soft sensor for estimating 4-CBA concentration, which could not be measured on-line in PX oxidation process. In this method, weak learners of BP neural networks were trained by part of samples selected by their weights and roulette wheel mechanism. The absolute values of last round training relative errors in weak learners were adopted to update weights of all training samples. Then, a second round updating on sample weights were completed by the product of original sample value and its weighting factor, which was defined by ratio of error range over dual thresholds. In the second updating process, weights were decreased for samples with gross errors but were increased for those with medium error. Consequently, probability of selecting outliers was reduced in following iteration of the training process. Five different methods were applied to model soft sensor of 4-CBA concentration with industrial data. Simulation results showed that the modified AdaBoost algorithm can improve soft sensor performance of 4-CBA concentration with predicting error less than that of other models.
AdaBoost algorithm; soft sensor; dual threshold technique; outliers; 4-CBA concentration; roulette wheel mechanism
10.11949/j.issn.0438-1157.20161609
TP 274
A
0438—1157(2017)05—2009—07
刘瑞兰(1972—),女,博士,副教授。
国家自然科学基金项目(61203213)。
2016-11-14收到初稿,2017-02-08收到修改稿。
2016-11-14.
LIU Ruilan, liurl@njupt.edu.cn
supported by the National Natural Science Foundation of China (61203213).
