公铁两用大桥桥面铺装力学行为研究
2017-10-13,,,
, , ,
(长沙市公路桥梁建设有限责任公司, 湖南 长沙 410205)
公铁两用大桥桥面铺装力学行为研究
李锋,胡红波,朱红军,曾宪群
(长沙市公路桥梁建设有限责任公司, 湖南 长沙 410205)
为研究公铁两用连续刚桁梁桥的公路桥面铺装结构的力学行为和力学指标,采用有限元软件ANSYS,建立简化桥面铺装的某公铁两用大桥整体有限元模型,对在简化铁路荷载和公路荷载作用下铺装结构的力学响应进行了分析,得到铺装层的应力 — 应变变化规律、力学控制指标和最不利荷位。分析结果表明: 采用3跨公路桥局部模型能获得相对合理的桥面铺装分析模型;各个轮载位的沥青面层最大横、纵向剪应力均出现在车轮荷载正下方沥青层与混凝土层交界处,计算结果显示沥青面层剪应力水平普遍于0.1~0.15 MPa之间,而SMA沥青混凝土与混凝土之间的抗剪强度为1 MPa,由此可见理论计算值满足容许值需求,并且留下了较大的抗剪储备空间。
公铁两用大桥; 桥面铺装; 模型简化; 力学行为
桥面铺装体系是桥梁行车系的重要组成部分,其必须具备保证行驶车辆安全舒适的基本能力,并且桥面铺装的疲劳耐久性和强度是影响桥梁整体功能性、经济效益和社会效益的重要指标[1]。尤其是针对大跨径桥梁的铺装体系,国内外多年的经验显示,大跨径桥梁的变形较大,与桥面铺装的协调性较差,通常在早期出现各种铺装层病害,同时因为交通量较大而提高了维修难度[2]。由此可见,桥面铺装的好坏在一定程度上制约了桥梁的建设和发展,对桥面铺装的忽视将会造成不必要的社会经济损失。
本文对某公铁共面连续钢桁架梁桥及“SMA沥青混凝土钢纤维轻质混凝土”组合铺装结构进行有限元模拟计算分析,得到该类桥型的自身特性和铺装层应力、应变变化规律,并对应各个力学控制指标找出最不利荷位,以期为类似桥梁的桥面铺装提供借鉴。
1 桥面铺装结构分析基本理论
铺装层相对而言是较为刚度较低的结构层,其通过摊铺压实而附着于钢桥面板之上,由于铺装层弹性模量远低于钢板而导致其受到正交异性钢桥面板特性的影响较为显著,钢桥面板结构上的微小变化都可能影响到铺装层,甚至钢桥面板的特性比铺装层本身的特性更为显著地影响铺装层受力状态,如:顶板厚度、纵肋间距等。因此,将铺装层按照刚度等效的方式等效为钢桥面板。通过分析简化后的结构受力状态,就能确定铺装层的受力状态了。分析时假设钢板与铺装层是完全连续的[3],则计算桥面顶板和铺装层的抗弯刚度值为:

(1)
式中:h为铺装层厚度;E为弹性模量;μ为泊松比。
分别计算钢桥面板以及铺装层抗弯刚度,并按照下列公式求和:
(2)
式中: 下标b为板的相关参数;下标p为铺装的相关参数;n为铺装层数。
依据抗弯刚度的等效规则,折算后的钢板等效厚度为:


(3)
进一步地,将铺装和顶板的自重折算到厚度h的等效层中,这时,替换后顶板密度计算公式为:
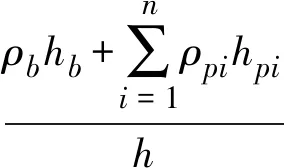
(4)
式中:h为计算出的等效厚度。
这样就按抗弯刚度等效的原则将结构上部的顶板和铺装组合层换算为厚度为h的单一等效层。这一等效层的模量与顶板钢板相同,厚度为等效厚度,密度为等效密度,在有限元计算过程中不必再对铺装层的影响作特殊考虑。
2 桥面铺装有限元分析
2.1 铁路荷载的简化
根据《铁路桥涵设计基本规范》中对铁路列车竖向静活载的规定,针对客运、货运铁路各自特点的不同原则所制定符合我国国情的铁路列车活载图式,中-活载图式如图1所示[4]。考虑到铁路桥为双向桥,因此将中活载分别采用集中力及均布力施加于最不利位置的铁路纵梁上。
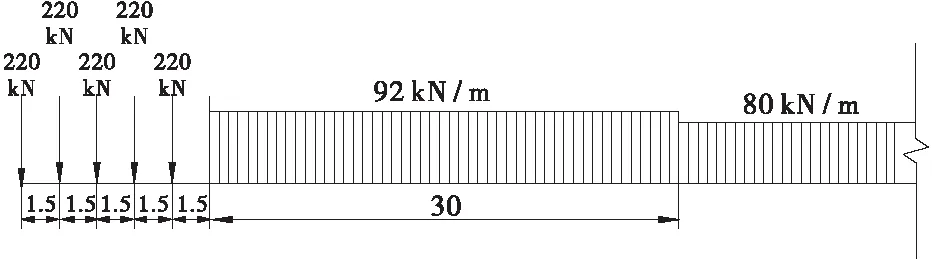
图1 “中-活载”图式(距离以m计)
2.2 公路荷载的简化
标准车辆荷载是设计公路桥梁的主要依据之一,直接关系到结构的可靠性和经济性。标准车辆荷载的制定应以桥梁之上的交通车辆现实行驶状态为评估参考,且需要对未来交通发展的增长性做出判断,标准车辆的主要技术指标如表1所示[5],分别对应前轴、中轴及后轴的重力标准值和车轮着地面积,前轮、中轮及后轮的荷载集度分别为0.25、0.5、0.58 MPa。考虑该桥最不利情况之下的承载情况,将车辆荷载根据规范满布于公路桥。

表1 车辆荷载的主要技术指标车辆重力标准值/kN前轴重力标准值/kN中轴重力标准值/kN后轴重力标准值/kN轴距/m轮距/m前轮着地宽度及长度/m中、后轮着地宽度及长度/m车辆外形尺寸/m550302×1202×1403+1.4+7+1.41.80.3×0.20.6×0.215×2.5
2.3 车轮荷载的简化
车辆轴载通过轮胎传递至铺装面层,而在轴载作用之下将会于轮胎与铺装面层之间形成一定范围的分布面积,其为轮胎与铺装面层的接触面积,亦称为轮印面积。轮印的形状近似椭圆形,其两半轴之比a/b在1.25~2.0之间[6],若车辆荷载增加,轮印面积也随之增大。
目前沥青路面设计规范中以BZZ — 100标准轴载为准,由于铺装层受力分析主要是局部问题,选用一组双轮荷载的单一轮胎作为研究对象即可[7]。由于考虑到复杂的轮印分布形式会给力学计算带来很大困难,并且对计算精度的增益效果并不明显,而矩形均布在理论分析及模拟计算时更容易运用[1],同时足够全面地呈现桥面铺装在车轮荷载作用下的变化规律,因此在模拟计算中把标准轴载的荷载分布形式简化成尺寸为200 mm×200 mm的矩形。
2.4 桥梁有限元模型
考虑到大桥南北两联相对独立,故而选取该桥其中一联建模。假定铺装层与钢桥面板之间变形协调并且完全连续,若铺装层采用实体单元计入全桥模型将导致计算量极为庞大,为简化计算,运用前述的桥面铺装刚度等效公式计算,将铺装层等效为正交异性钢桥面板的一部分,从而只需要建立正交异性钢桥面板及桁架桥即可。建模如图2、图3。

图2 全桥模型局部示意

图3 全桥模型横断面
3 桥面铺装子模型分析
3.1 子模型几何尺寸分析
对于大跨径桥梁而言,车轮荷载作用下的桥面铺装受力状态主要是局部承载分析[4],如果用全桥模型进行分析,为了得到桥面铺装相对准确的变形及内力则需要较为精细的网格,这样导致了计算效率极其低下,因此,使用网格较为精细的局部模型对钢桥面板和铺装层进行有限元建模分析是较为经济的选择。
大桥采用“SMA沥青混凝土+钢纤维轻质混凝土”的组合体系铺装方案,很大程度上提高了铺装层与正交异性钢桥面板的整体性与刚度,因此,铺装层的局部效应受到大幅削弱。为了避免有限元分析模型的边界条件对结构的计算结果造成过大误差,以三角托架之间的距离8 m为一基本跨,分别选取公路桥局部结构:1跨8 m模型、3跨24 m模型、5跨40 m模型,通过有限元软件ANSYS建立分析模型,如图4所示。车轮荷载施加于中跨的跨中,并提取沥青面层及混凝土铺装下层的最大横向拉应力、最大纵向拉应力和沥青面层相对挠度三项针对铺装层而言较为重要的参数指标,计算结果见表2。
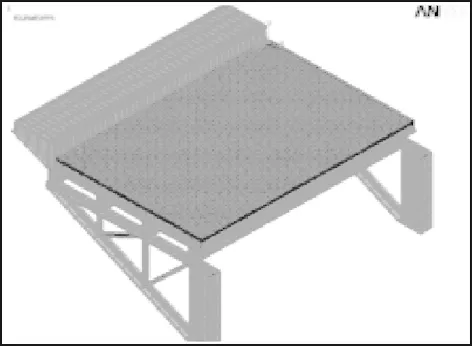
a) 1跨

b) 3跨c) 5跨
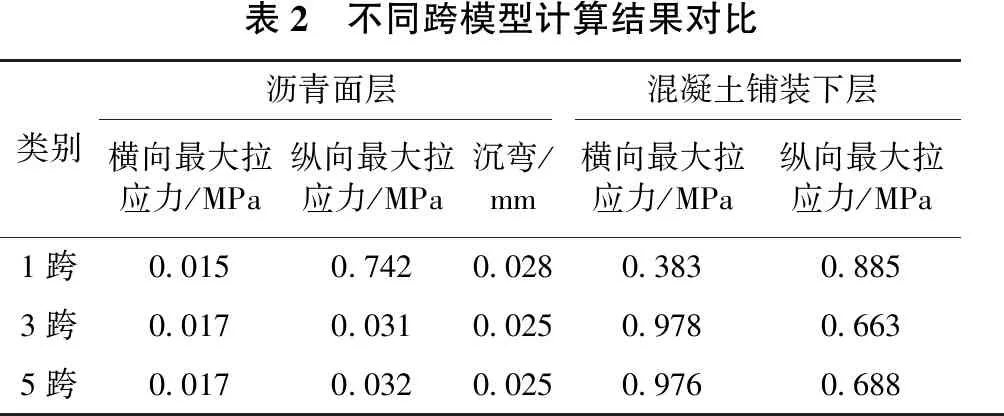
表2 不同跨模型计算结果对比类别沥青面层混凝土铺装下层横向最大拉应力/MPa纵向最大拉应力/MPa沉弯/mm横向最大拉应力/MPa纵向最大拉应力/MPa1跨001507420028038308853跨001700310025097806635跨00170032002509760688
通过对比分析上表数据,可以得知1跨模型受到两端边界条件的影响较为严重,沥青面层纵向最大拉应力、混凝土过渡层横向最大拉应力均出现数值异常,模型尺寸效应明显。3跨模型与5跨模型各项收敛结果较为接近,最大误差未超过5%,尽管继续增大模型尺寸会得到更好的计算结果,但是综合考虑计算成本和时间成本,选用3跨模型既能得到较为精确的计算结果,也能提升计算效率,有助于后期优化处理。
3.2 沥青面层受力分析
大桥的公路桥横桥方向并不具备对称性,为分析车轮荷载沿横桥方向改变时所引起的铺装层应力变化规律,故于横桥方向的行车道之内布置5个横向轮载位,相邻横向轮载位的中心间距为300 mm,如图5所示,横向轮载位H1、H3、H5于公路纵梁之间,横向轮载位H2、H4于公路纵梁之上。
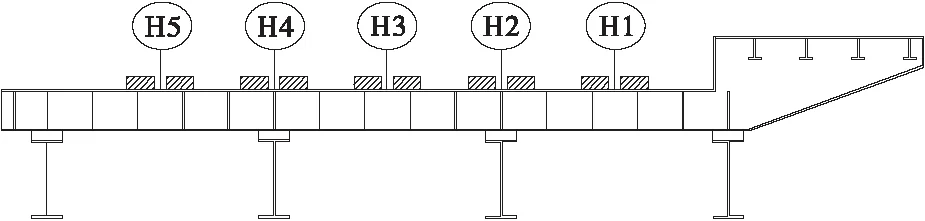
图5 横向轮载位分布
通过上节的分析,选用3跨段模型可以有效降低模型的尺寸效应的同时又能得到相对精确的计算结果,纵向轮载以中跨的为主。由中跨1/2处至中跨端部共布置9个纵向轮载位Z1至Z9,其分别对应中跨1/2处、中跨9/16处、中跨10/16处、中跨11/16处、中跨12/16处、中跨13/16处、中跨14/16处、中跨5/16处、中跨端部,相邻纵向轮载位的中心间距为500 mm,纵向轮载位Z1位于中跨1/2处的横隔板之上,纵向轮载位Z9位于中跨端部的横隔板之上。枝城大桥公路桥局部模型根据该桥施工图纸所提供的尺寸参数及材料参数建立,由于中跨1/2处至中跨端部具备纵向重复性,故而分析该部分桥面铺装受力状态可以拓展至全桥。因此,将每个横向轮载位都按照纵向轮载位的分布,施加简化轮载,共计45个轮载位,各个轮载位通过横向位置H1~H5及纵向位置Z1~Z9表示,如图6所示。通过之前的分析指标分别统计沥青面层和混凝土铺装下层的最大横向拉应力、最大纵向拉应力、最大横向剪应力、最大纵向剪应力及表面沉弯。通过分析横向轮载位于纵向分布上的应力变化规律,找出对应各指标下的最不利轮载位,并以该轮载位作为分析铺装层参数的轮载位。

图6 轮载位示意图
通过对公路桥局部模型进行计算,沥青面层横向、纵向最大拉应力趋势见图7、图8。不同横向轮载位沿桥面纵向移动时,位于公路纵梁之间的横向轮载位H1、H3、H5的沥青面层最大横向拉应力变化规律一致,位于公路纵梁之上的横向轮载位H2、H4的沥青面层最大横向拉应力变化规律一致;而当横向轮载位H1至H5沿桥面纵向移动时,沥青面层最大纵向拉应力变化规律均呈一致趋势。
横向轮载位H1、H3、H5的沥青面层最大横向拉应力发生于最靠近横隔板的纵向轮载位Z8;横向轮载位H2、H4的沥青面层最大横向拉应力发生于横隔板之上的纵向轮载位Z9,且于最靠近横隔板的纵向轮载位Z8达到最小值。且轮载位H1-Z8最大横向拉应力是轮载位H5-Z8最大横向拉应力的1.36倍。

图7 沥青面层最大横向拉应力

图8 沥青面层最大纵向拉应力
横向轮载位H1至H5的沥青面层最大纵向拉应力均发生于横隔板之上的纵向轮载位Z9,表明横隔板一定程度上增强了其周围纵向加劲肋及钢桥面板的刚度,导致靠近横隔板位置的纵向拉应力水平较高。且轮载位H4 — Z9最大纵向拉应力是轮载位H5-Z9最大纵向拉应力的2.39倍。
通过计算分析发现,横隔板之上的轮载位Z1、Z9沥青面层最大横向、纵向拉应力均出现在双轮之间,沥青面层于轮载作用下的局部效应相当显著;横隔板之间的各个轮载位加载作用下沥青面层最大横向、纵向拉应力均出现在中跨端部横隔板与公路纵梁经由高强螺栓固定处的正上方。沥青面层拉应力整体水平较低,最大横、纵向拉应力都在0.1 MPa以内,远低于SMA沥青混凝土疲劳抗拉容许值0.56 MPa,并且分布较为均匀,说明了弹性模量较高的混凝土作为铺装下层很大程度上削弱了车轮荷载对铺装层造成的局部效应,使得铺装层刚度增大、钢板的整体性增强以及大大降低了纵肋和横隔板对车轮荷载的敏感性,改善了沥青面层的承载环境,减轻了正交异性钢桥面板的承载负担,车轮荷载通过铺装层更为均匀地传递到正交异性钢桥面板。部分轮载位的沥青面层横向、纵向拉应力云图如图9和图10所示。


a) 横向拉应力b) 纵向拉应力


a) 横向拉应力b) 纵向拉应力
沥青面层与混凝土铺装下层间横、纵向最大剪应力计算结果如图11和图12所示。当横向轮载位H1至H5沿桥面纵向移动时,于横隔板处的纵向轮载位剪应力水平较低,于横隔板之间的纵向轮载位呈现较为复杂的跌宕变化趋势。横向轮载位H2、H4于沥青面层横、纵向剪应力水平都高于横向轮载位H1、H3、H5的沥青面层横、纵向剪应力。
横向轮载位的沥青面层最大横向剪应力于纵向轮载位Z3至Z7之间呈现相反的跌宕方向,而在逐渐靠近横隔板时应力水平逐渐降低。轮载位H2-Z4的最大横向剪应力是轮载位H5-Z5最大横向剪应力的1.12倍。
横向轮载位H1至H5于横隔板之上的沥青面层最大纵向剪应力骤然降低,而于横隔板之间呈现较为复杂的跌宕趋势,轮载位H2-Z8最大纵向剪应力是轮载位H5-Z7最大纵向剪应力的1.03倍。

图11 沥青面层最大横向剪应力
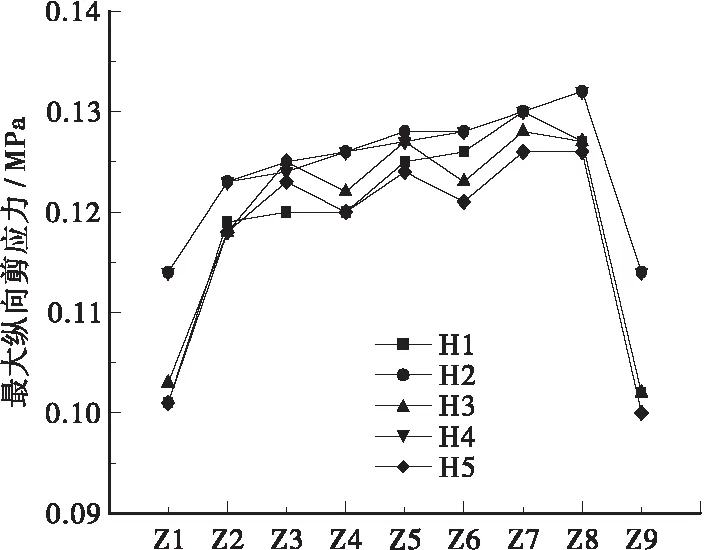
图12 沥青面层最大纵向剪应力
各个轮载位的沥青面层最大横、纵向剪应力均出现在车轮荷载正下方沥青层与混凝土层交界处,应力云图如图13所示,计算结果显示沥青面层剪应力水平普遍于0.1~0.15 MPa之间,而SMA沥青混凝土与混凝土之间的抗剪强度为1 MPa,由此可见理论计算值满足容许值需求,并且留下了较大的抗剪储备空间。计算结果表面,沥青面层拉应力最不利轮载位选取轮载位H4 — Z9,应力值为0.091 MPa;铺装层层间剪应力最不利轮载位选取轮载位H2 — Z4,应力值为0.145 MPa,沥青面层最不利荷位图示如图14所示。


a) 横向剪应力b) 纵向剪应力
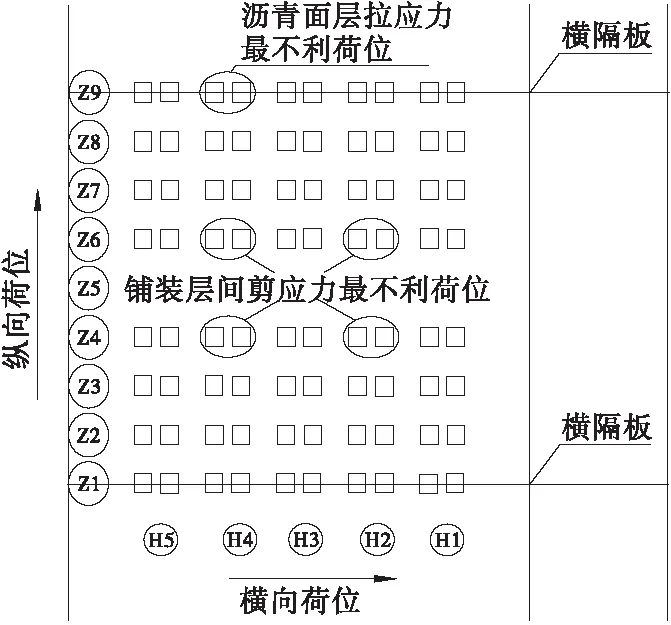
图14 沥青面层最不利荷位
4 结论
1) 通过对比沥青面层计算结果,横隔板之上的轮载位沥青面层最大横向、纵向拉应力均出现在双轮之间,沥青面层于轮载作用下的局部效应相当显著。
2) 横向轮载位H1至H5的沥青面层最大纵向拉应力均发生于横隔板之上的纵向轮载位Z9,表明横隔板一定程度上增强了其周围纵向加劲肋及钢桥面板的刚度,导致靠近横隔板位置的纵向拉应力水平较高。
3) 横向轮载位的沥青面层最大横向剪应力于纵向轮载位Z3至Z7之间呈现相反的跌宕方向,而在逐渐靠近横隔板时应力水平逐渐降低;轮载位H2-Z4的最大横向剪应力是轮载位H5-Z5最大横向剪应力的1.12倍。
4) 各个轮载位的沥青面层最大横、纵向剪应力均出现在车轮荷载正下方沥青层与混凝土层交界处,计算结果显示沥青面层剪应力水平普遍于0.1
MPa至0.15 MPa之间,而SMA沥青混凝土与混凝土之间的抗剪强度为1 MPa,由此可见理论计算值满足容许值需求,并且留下了较大的抗剪储备空间。
[1] 黄卫.大跨径桥梁钢桥面铺装设计理论与方法[M].北京:中国建筑出版社,2006.
[2] 李昶,顾兴宇.大跨径钢桥桥面铺装力学分析与结构设计[M].南京:东南大学出版社,2007.
[3] 张培森. 车辆荷载作用下沥青路面结构应力分析[D].西安:长安大学,2007.
[4] 顾兴宇,邓学钧,周世忠,等.钢桥面系统各项参数敏感性分析[J].城市道桥与防洪, 2008(12):96-98.
[5] 张德佳,叶奋,袁金凤,等.基于实桥加载的钢桥面铺装数值模型优化[J].公路交通科技,2013,30(7):103-106.
[6] 钱振东,刘云,郑斌. 大跨度公铁两用斜拉桥公路桥面铺装层受力特点分析[J].土木工程学报,2011(6):138-142.
[7] 陈磊磊,钱振东,王建伟,等.武汉天兴洲公铁两用长江大桥钢桥面环氧沥青混凝土铺装设计与施工[J].桥梁建设,2011(1):79-82.
1008-844X(2017)03-0129-06
U 448.12+1
A
2017-08-07
李 锋(1978-),男,工程师,主要从事路桥建设。
