基于林分平均直径的二类小班调查和系统抽样数据的融合

肖云丹 侯瑞霞 纪平



基于林分平均直径的二类小班调查和系统抽样数据的融合

肖云丹 侯瑞霞 纪平*

（中国林业科学研究院资源信息所 北京 100091）

林分平均直径是评价立地生产力的一个重要指标。通过系统样地调查和二类调查数据均可得到林分平均直径。那么该如何做到二类调查数据到系统样地的融合？利用贝叶斯法构建了基于2004年和2009的二类调查数据的林分平均直径模型，然后通过该模型预测2011、2013年的林分平均直径，并与这两年的系统样地数据建立融合模型，研究得到融合模型效果较好（R2=0.5861）。

林分平均直径；二类调查；系统样地；融合

1 引言

融合，顾名思义就是将不同来源的数据进行联合，达到互通互推的目的。随着森林资源调查数据的多元化，监测到的数据不断增多，数据之间不可避免的存在冗余、互补。数据融 合将林业遥感和地面监测数据综合互补，消除冗余，从而降低不确定性，使得森林资源监测更准确可信。王臣立[1]以雷州林业局2002年一类清查数据以及地面调查数据作为地面数据源，融合LANDSAT-TM和RADARSAT-SAR估算了研究区热带人工林的净初级生产力，为热带森林NPP的研究提供了一个好思路。李旺等[2]利用机载激光雷达点云数据，融合大量实测单木结构信息估计了森林地上生物量。刘峰等[3]以雪峰山武冈林场为研究对象，融合遥感数据和地面实测样地数据，研究机载激光雷达估测中亚热带森林乔木层单木地上生物量的能力，并得到了较好的结果。

众所周知，我国森林资源调查主要分为三类：森林资源清查（简称一类清查）、森林资源规划设计调查（简称二类调查）和作业调查。对于前两类森林资源调查，我们讨论得比较多。一类清查的目的是及时、准确地查清全国森林资源的数量、质量及其消长动态，并进行评价。二类调查是以国有林场、自然保护区、森林公园等森林经营单位或县级行政区域为调查单位，以满足森林经营方案、总体设计、林业区划与规划设计需要而进行的森林资源调查，主要是查清森林资源的种类、数量和质量，以及相关的状况[4]。相对于一类清查工作而言，二类调查的展开过程要详细得多。这是一种对当地森林资源进行逐一排查，并进行累加统计的调查方法。然而这两类调查各有利弊[5]。二类调查由于多控制在地方上，因而常因为资金等问题难以得到开展。因此，在实际工作过程中，应当与一类清查所获得的数据进行融合，有的放矢，做到一类和二类数据的信息互补，减少调查成本。一类清查典型的特征就是系统固定样地调查。本研究将以中国林业科学研究院热带林业实验中心为研究地点，以林分平均直径为研究对象，做到二类小班调查和系统固定样地数据的融合。

2 研究区域及数据获取

2.1 二类调查数据

搜集到实验地2004年二类调查矢量数据和2009年二类调查矢量数据。

2.2 系统样地数据

该数据是试验地管理部门在生产中自己设计调查的，共设计了238个样地，每两年调查一次。本研究搜集到实验地2011年系统样地数据、2013年系统样地数据。

其中调查内容主要是：对样地概况、样地数据加工、每木调查、幼树数据、幼苗数据、草木数据、灌木数据、枯落物和土壤结构、进界木、林下特征注记、圆形样地结构、样地林分影像调查记录等内容进行详细的调查。

3 研究方法

3.1林分平均直径模型的建立

利用中国林科院热带林业实验中心二类调查数据或系统抽样数据为研究对象，以林分胸高断面积、林龄等为自变量构建林分平均直径模型，为预测林分平均直径生长动态变化服务，模型如下：

式中：1、2分别为第1、2期林分平均直径(cm)；

1、2分别为第1、2期林分平均年龄；

1、2分别为第1、2期林分胸高断面积(m2/ha)；

1…5为待估参数。

3.2 贝叶斯理论

令y= (y1, y2, y3, …)为数据向量，=(1,2,3, …)为参数向量，则根据贝叶斯理论，其基本公式为：

式中，p为概率分布函数或者密度函数。由这公式可以看出，不管是模型参数还是样本都看作是随机变量。根据贝叶斯条件概率，则对方程（2）变式为：

(3)

其中对于连续型，

3.3 贝叶斯法与传统方法的区别

贝叶斯方法是基于贝叶斯定理而发展起来用于系统地阐述和解决统计问题的方法。一个完全的贝叶斯分析（full Bayesian analysis）包括数据分析、概率模型的构造、先验信息和效应函数的假设以及最后的决策[6]。近些年，根据文献报道，贝叶斯法（Bayesian method）是估计模型参数和评价其不确定性的一个不同方法，已经在环境、生态、医疗、水文、林业等研究领域得到了广泛应用[7-12]。贝叶斯推断的基本方法是将关于未知参数的先验信息与样本信息综合，再根据贝叶斯定理，得出后验信息，然后根据后验信息去推断未知参数[13]。贝叶斯推断在统计推断的研究比起传统推断法有以下三点优势：贝叶斯推断法综合利用了先验信息和样本信息，先验信息（分布）可以来自历史资料（文献）或者主观信念，它是在进行统计推断时的一个必要因素，而传统法仅仅利用了样本信息，缺乏先验信息的设定；贝叶斯法把样本和参数看作是随机变量，并且一般假设服从正态分布；而传统法把未知参数估计值看作固定值，并没有对参数或模型的构造加以限制[14,15]。

3.4 贝叶斯模型的估计方法

在贝叶斯统计中，通过对高维概率分布函数进行积分，推断或预测总体参数。但在许多情况下，因为它并没有或很难写出明确的解析表达式，致使这种积分很难进行。所以解决这一难题用数值积分比较困难而且不够准确，尤其当维数较大时更是如此。这种情况下，我们会选择一种简单且行之有效的贝叶斯计算方法即马尔科夫链蒙特卡洛（MCMC）方法，而吉布斯抽样算法（Gibbs sampling）是一种特殊的MCMC算法，其中最重要的软件包是WinBUGS，它是基于吉布斯抽样估计的贝叶斯模型。

3.5 先验分布

先验分布的选择在贝叶斯方法中是非常重要的[16]。在上述的林分平均直径模型中，我们需要为参数p1…p4选择合适的先验分布。许多学者选择利用无信息先验分布（non- informative prior），该信息可以忽略不计，而且对参数估计的影响不大。对于无信息先验分布，我们一般选择均值为0，方差足够大的能够覆盖整个数据范围的正态分布[17]。当然也可以选择有信息先验分布（informative prior）作为贝叶斯方法中的先验分布，这些信息可以来自主观信念或者历史文献资料。本研究首先通过传统估计方法估计林分平均直径模型的参数，然后以这些参数估计值为贝叶斯估计方法的先验信息分布重新估计林分平均直径模型，以期得到更精确的估计值。在进行贝叶斯估计时，为了保证迭代收敛和得到稳定的参数后验概率值，迭代次数设为30万次，并去掉前面的5万次退火（burn-in）迭代。

对于模型模拟效果的评价，本研究采用决定系数（R2）、均方根误差（RMSE）2个拟合统计量指标评价。对于数据的融合，首先通过2004年、2009年2期二类小班调查数据建立林分平均直径模型，并通过该模型预测2011年、2013年各小班的林分平均直径；接着利用系统样地2011年、2013年调查的实际值与通过二类调查数据预测所得值进行验证，并建立线性回归模型，实现二类小班调查数据到系统样地数据的融合。

4 研究结果

4.1 模型估计

首先利用非线性最小二乘法估计（proc nlin模块，SAS）林分平均直径模型，得到参数估计值，见表1。由表1发现，模型的各参数均在0.05水平上表现出显著性。其次，根据表1中林分平均直径模型的估计值和标准误，作为林分平均直径模型参数的先验信息分布，利用贝叶斯法估计林分平均直径模型参数的后验分布。

表1 基于二类调查数据建立的林分平均直径模型参数估计值（传统估计法）

图1是贝叶斯方法估计林分平均直径模型参数的迭代过程图。由图2可发现，林分平均直径模型参数估计比较平稳。

图1贝叶斯方法估计林分平均直径模型参数的迭代过程图

图2是林分平均直径模型通过贝叶斯估计法计算所得的参数估计值的后验概率图。根据图2可以发现，是林分平均直径模型通过贝叶斯估计法计算所得的参数估计值的后验概率图。根据图1可以发现，林分平均直径模型的参数估计出现一定的不确定性，参数估计值不是一个固定值，而是服从一定的分布。图3是通过贝叶斯估计方法估计林分平均直径模型，所得的决定系数R2平均值为0.6136，均方根误差RMSE平均值为3.0325，而且经过F检验，差异显著（P值<0.01）。因此，建立的林分平均直径模型表现较好，可以很好地预测下期的林分平均直径生长量。

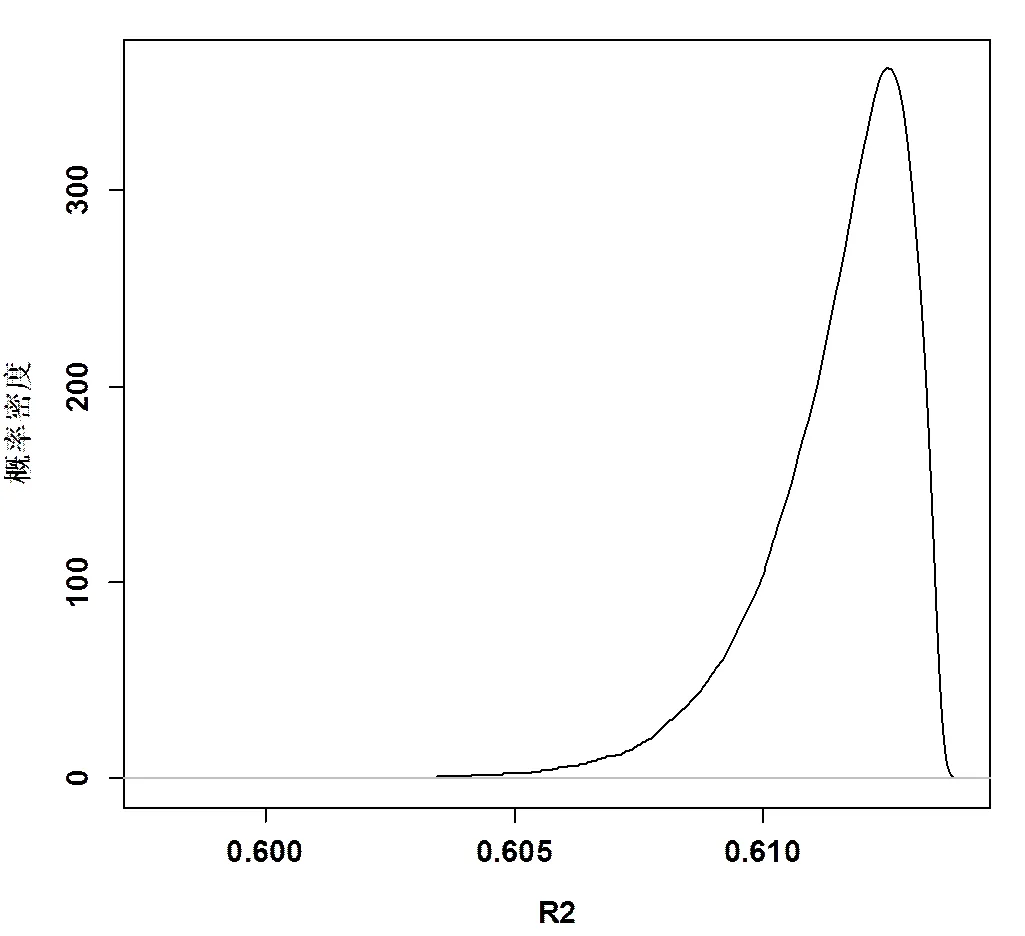
图3林分平均直径模型2和的后验概率图

4.2 二类数据到系统样地的融合

基于2004年和2009年二类调查数据，构建林分平均直径模型，并通过贝叶斯法估计模型参数。之后，利用建立好的模型预测2011年和2013年各小班的动态变化情况。模型中，下标s表示的是二类数据，下标p表示的是系统样地数据。

林分平均直径融合模型：

由图4发现，基于二类数据建立的林分平均直径模型预测所得的2011年和2013年小班林分平均直径和实际调查的林分平均直径线性相关性比较高，建立的线性回归模型拟合精度相对较好。因此，这两种来源的数据从二类调查到系统样地融合效果较好。

图4林分平均直径融合模型相关图

5 小结与讨论

随着森林资源监测调查数据的多元化，所获得的数据不断增多，数据之间不可避免的存在冗余、互补。数据融合将多种来源数据综合互补，消除冗余，从而降低不确定性，使得森林资源监测更准确可信。本研究对中国林科院热林中心二类调查数据和系统样地数据两种来源的数据进行融合，实现不同来源数据的互推转化，建立融合模型，节省调查成本。本研究所建立林分平均直径模型模拟精度较高，而且经过F检验，差异显著。此外，在本研究中引进了贝叶斯理论，利用贝叶斯法估计林分平均直径模型参数，给出了林分平均直径模型参数的后验概率分布，能够很好地描述出模型的不确定性，更能符合实际的林木生长状况。

基于林分平均直径从二类调查数据到系统样地数据的融合，得到以下融合模型：

林分平均直径融合模型：

通过以上融合模型可发现，林分平均直径融合模型R2超过了0.58，精度较高。因此，我们可以通过系统样地调查数据推断得到二类调查小班的林分平均直径，大大节省了调查成本，这未尝不是个好的方法。

[1] 王臣立．雷达与光学遥感结合在森林净初级生产力研究中应用[J]．中国科学院研究生院，2006．

[2] 李旺，牛铮，高帅，等．机载激光雷达数据分析与反演青海云杉林结构信息[J]. 遥感学报，2013，17（6）：1612-1626.

[3] 刘峰，谭畅，雷丕峰．中亚热带森林单木地上生物量的机载激光雷达估测[J]．应用生态学报，2014，25（11）：3229-3236．

[4] 孟宪宇．测树学[M]．北京：中国林业出版社，1996．

[5] 范佐齐．森林资源一类清查和二类调查的对比讨论[J]．科技与生活，2012，（21）：212-212．

[6] Lindley DV. Bayesian thoughts [J]. Significance, 2004, 1(2): 73-75.

[7] Lamon E C, Clyde M. Accounting for model uncertainty in prediction of chlorophylla in Lake Okeechobee. ISDS Discussion Paper 1998, 98-42.

[8] Clyde M. Model uncertainty and health effect studies for particulate matter. Technical Report Series, NRCSE-TRS No. 1999,027.

[9] Ellison A M. Bayesian inference in ecology. Ecology letters, 2004, 7(6): 509-520.

[10] 李向阳. 水文模型参数优选及不确定性分析方法研究[D]. 大连：大连理工大学博士学位论文，2005.

[11]Bullock B P, Boone E L. Deriving tree diameter distributions using Bayesian model averaging. Forest Ecology and Management, 2007, 242 (2-3): 127-132.

[12]Zhang X, Duan A, Zhang J. Tree biomass estimation of Chinese fir (Cunninghamia lanceolata) based on Bayesian method. PLOS ONE, 2013, 8(11): 1-7.

[13]茹诗松等．高等数理统计[M]．北京：高等教育出版社，1998．

[14]张雄清，张建国，段爱国．基于贝叶斯法估计杉木人工林树高生长模型[J]．林业科学，2014，50（3）：69-75．

[15]张雄清，张建国，段爱国．杉木人工林林分断面积生长模型的贝叶斯估计[J]．林业科学研究，2015，28（4）：538-542．

[16]Gelman A, Carlin JB, Stern HS, Rubin DBBayesian Data Analysis, 2nd edn [M]. Boca Raton, FL, USA: Chapman and Hall/CRC.,2004.

[17]Ellison AM. Bayesian inference in ecology [J]. Ecology letters, 2004, 7(6): 509-520.

Data fusion of stand mean diameter based on forest resource inventory data for management and systematic plots

Xiao Yundan, Hou Ruixia, Ji Ping

Stand mean diameter is an important index for evaluating site productivity, which could be obtained from forest resource inventory data for management (FIDM) and systematic plots. How to make the data fusion of these two data sources? In this study, we developed Stand mean diameter model based on the FIDM data using Bayesian method, and predict the stand volume in 2011, and 2013. Then we make the data fusion with systematic plots in 2011, 2013. Results showed that the data fusion model performed well (2=0.5861)

stand mean diameter, forest resource inventory data for management, systematic plots, data fusion

TP392

A

1004-7743（2017）02-0071-06

2017-03-23

中国林科院基本科研业务费专项经费项目（CAFYBB2017QA010）

肖云丹，女，1982年10月生，中国林科院资源信息所，助理研究员，E-mail: xiaoyd@ifrit.ac.cn

纪平，研究员