水下爆炸柱型装药与球形装药远场等效关系

张弛宇, 郭 锐, 刘荣忠, 陈 亮, 杨永亮



水下爆炸柱型装药与球形装药远场等效关系

张弛宇, 郭 锐, 刘荣忠, 陈 亮, 杨永亮

(南京理工大学机械工程学院, 江苏南京, 210094)

柱型战斗部和球形战斗部作为2种最常规战斗部形式, 其水下爆炸性能是其研究的重点, 目前已存的水下爆炸经验公式皆为球形装药。为研究柱型装药水下爆炸压力场是否也存在类似球形场的经验公式, 文中首先定性分析了作用方位和长径比对柱型装药水下爆炸压力场的影响。通过对比分析柱型装药和等药量球形装药压力场, 求得柱型装药与球形装药远场冲击波关系式方程, 并结合球形装药经验公式, 推导得到柱型装药压力场近似经验公式。仿真试验验证了上述公式的准确性。文中的研究可为优化水下战斗部爆炸性能提供依据。

水下爆炸;柱型装药;球形装药;经验公式

0 引言

水下爆炸是水下武器及水下防护的基本课题,研究方向主要为炸药的爆轰研究、冲击波的产生和传播以及气泡脉动的研究。球型装药作为战斗部一种主要形式, 研究比较广泛, 且目前已存的经验公式皆为球形装药。而柱型装药由于其长径比变化多, 很难通过单一的研究判断其压力场规律。Sternberg[1]用2D轴对称Lagrange方法计算了不同长径比的柱型装药水中爆炸压力分布, 表明冲击波参数受长径比控制, 且指出长径比接近1时, 冲击波可以近似为球形。Hammond[2]对柱型炸药的研究表明, 虽然装药形状对水中爆炸冲击波有很大影响, 但超过一定距离时, 柱型炸药冲击波场可以用等质量球形炸药近似, 与Sternberg研究相同。侯俊亮[3]通过数值仿真研究了不同形状装药爆炸冲击波场及对靶板作用效应。李金河[4]等人用试验方法研究了柱形装药水下爆炸轴向和径向冲击波峰值变化, 表明其仍然符合相似律和指数衰减规律。但上述研究均未得出柱型装药冲击波压力场经验公式。

文中基于数值仿真, 通过对比、分析固定长径比柱型TNT装药与球形装药的冲击波压力场, 得出一种具有普遍意义的柱型装药和球形装药远场冲击波等效关系, 并结合球形装药经验公式, 推导出柱型装药压力场近似经验公式, 为后续科学研究提供了理论依据。

1 水下爆炸Colo经验公式

目前关于水下爆炸冲击波最常用的公式多采用Colo总结的经验公式[5], 具体如下

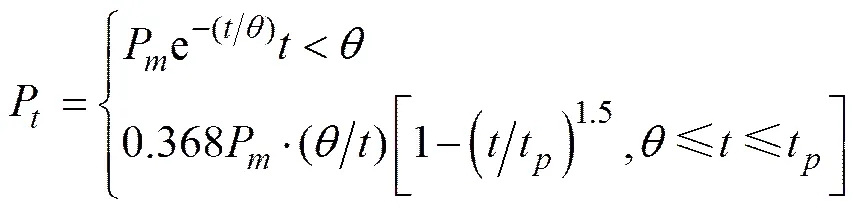
(2)

(3)

式中: P为冲击波压力峰值压力;P为冲击波压力;为衰减系数;为爆距;0为药包半径;为TNT质量。

2 仿真模型和状态方程

2.1 炸药的状态方程

炸药采用JWL方程

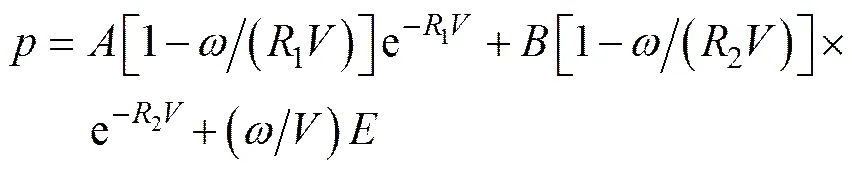
式中:为压力;为相对体积;为炸药内能;,均为材料参数;1,2和为常数。

TNT状态方程参数见表1。表中:为炸药密度;为爆热。

表1 TNT状态方程参数

2.2 水的状态方程

水采用SHOCK状态方程

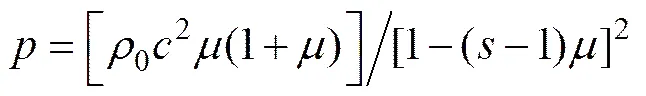
2.3 计算模型

图1为柱型装药有限元模型[6], 水域的大小为2 400×1 200, 装药为29 gTNT装药, 模型关于轴中心对称, 水域和炸药均采用欧拉网格。

边界条件设置为Flow-out。定义中心起爆方式, 炸药中心点为坐标原点(0,0), 炸药轴向(水平方向轴)为0°, 炸药径向(竖直方向轴)为90°, 同一半径上相邻的监测点间距22.5°, 相邻半径上同一方向角监测点间距250 mm, 共设置20个监测点。

图2为球形装药有限元模型[7], 采用1D楔形模型, 边界条件设为全流出边界条件, 楔形长度为3 000 mm。

3 仿真结果与分析

3.1 柱型装药和球形装药等效关系式

Sternberg[1]指出柱型装药冲击波峰值压力与爆距、作用方向及长径比()有关。设柱型装药冲击波峰值压力为(,,)。球形装药冲击波峰值压力为()。

以=13/3的柱型TNT装药为代表, 根据AUTODYN仿真得出装药在不同爆距和方向角(,)下的冲击波峰值压力(MPa), 如表2所示。

表2 柱型装药(L/D=13/3)不同爆距方向角时冲击波峰值压力

表3为球形TNT装药在不同爆距的冲击波峰值压力大小。

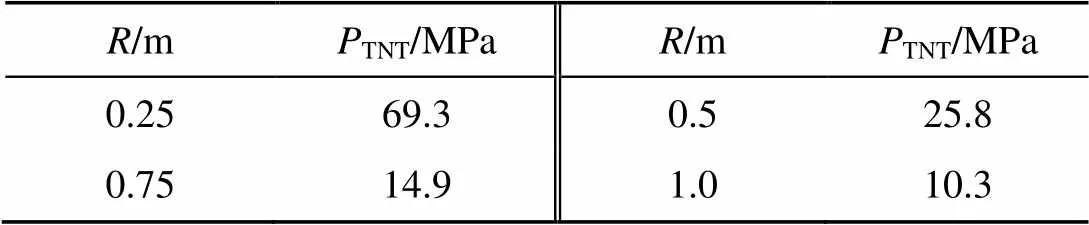
表3 球形装药不同爆距时的冲击波峰值压力

对比表2和表3可知, 此布置下的柱形装药在径向(90°方向)产生的冲击波峰值压力大于等质量同位置的球形装药, 径向峰值压力最少提高了约10%, 在装药轴向(0°)同距离处冲击波峰值压力小于球形装药, 故推测爆炸远场存在一点, 使得此处柱型装药和球形装药爆炸冲击波峰值压力相同, 在此可用柱型冲击波完全代替球形[8]。

图3为1/4柱型装药(/=13/3)和球形装药爆炸云图。可以看出, 球形装药冲击波以球形传播, 当爆距较小时, 柱型装药冲击波云图近似为矩形, 随爆距增大, 趋于球形, 当爆距达到一定距离时, 继续以球形传播形式传播[5]。这是由于水的可压缩性很小, 当爆距较小时, 装药形状对爆炸影响很大, 在爆距较远时, 装药形状几乎不构成影响[9]。

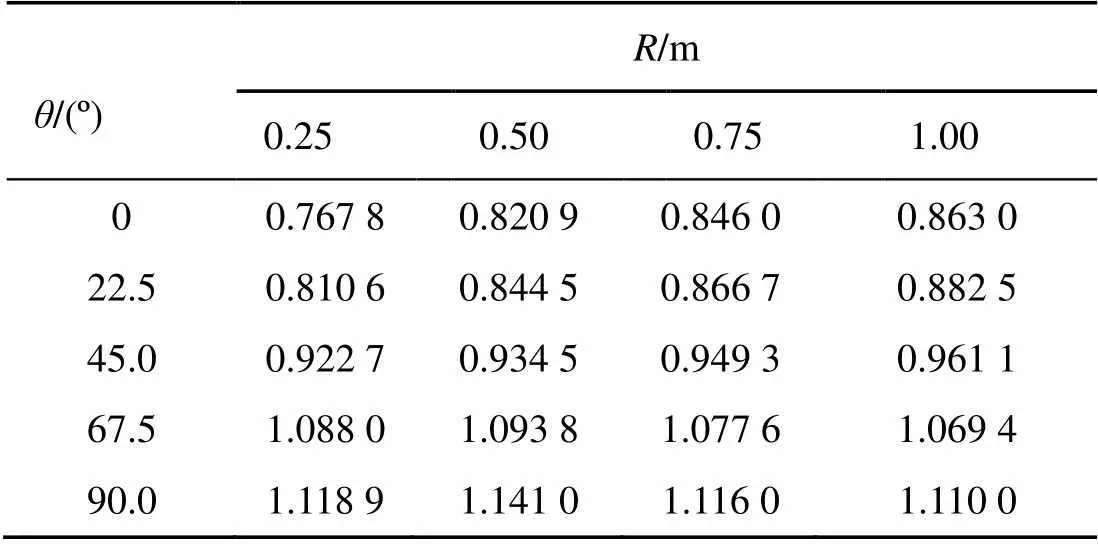
表4 柱型装药(L/D=13/3)和球形装药冲击波峰值压力比值

由图4可知, 不同爆距下的冲击波峰值压力比值随方向角的增大, 呈现出先分散后重合的特征, 且不同爆距的映射曲线上随角度的递增几乎都交于一点, 证明了在爆炸某处, 柱型装药在此处产生的冲击波峰值压力与球形装药完全相同, 验证了以上推测[10]。

以相同的试验方法, 分别得到/=7/3时和/=19/3时柱型装药的爆炸云图和压力比值曲线, 见图5。

图6和图7分别为2种柱型装药与球形装药冲击波峰值压力比值曲线走势图。

对比图4~图7可知, 不同长径比的柱型装药爆炸近场均近似以柱型传播, 远场以球形传播。且随着长径比的增加, 轴向冲击波峰值压力减少, 径向峰值压力增加, 这是由于柱型装药几何特点造成爆炸冲击波的叠加, 当长径比无穷大时, 装药近似线性, 能量几乎集中在径向。

以=13/3的柱型装药为例, 根据冲击波峰值压力比值走向, 取傅里叶函数表示该曲线, 设

将表4不同点的比值系数带入方程,θ为比值系数为1时对应所得角度。通过拟合, 得到函数未知数(,,),见表5。

表5 不同爆距下方程未知数拟合结果

由表5数据知, 通过拟合得(0.25 m, 46.2º)、(0.5 m, 49.698º)、(0.75 m, 48.859º)、(1.0 m, 48.976º)处柱型装药产生的冲击波峰值压力与球形装药完全相同。

为了得到柱型装药在不同(,)的与球形装药的关系, 进一步分析表5数据。未知数稳定在2.23附近, 取=2.23;也相对稳定, 取为48º;在公式中影响因素不超过3%, 可忽略不计。因此, 冲击波峰值比值走向方程

(8)

故, 在极坐标下, 柱型(/=13/3)装药与球形装药冲击波峰值关系式

为了验证柱型装药与球形装药关系式的准确性, 将柱型装药和球形装药拟合公式结果与球形装药结果进行对比。

表6为根据式(6)~式(9)计算所得不同爆距方向角(,)时的映射系数(,)值。

表6 不同爆距方向角的映射值

通过仿真验证, 由柱型装药和球形装药关系所得出的数据与AUTODYN所得出数据除(,)在(0.2 m, 0)处误差超过5%, 其余点均小于5%,见表7, 原因在于: 1) 根据图3映射系数走势, 方向角较小时, 映射曲线分散大, 因此按照假设拟合产生的误差也大; 2) 在大长径比情况下, 近距离的轴向和径向所受长径比的影响较大。

表7 柱形装药和球形装药等效关系式验证结果

注:

以相同的方法分析/=7/3和/=19/3时的柱型装药也满足要求, 总的来说, 基于仿真得出柱型装药和球形装药冲击波峰值关系式满足要求, 证明了关系式的准确性。

3.2 柱型装药远场压力场分析

为得出柱型装药远场冲击波压力场经验公式, 将柱型装药和球形装药等效关系式与Cole经验公式对比, 见表8。表中,TNT为仿真数据;P为经验值计算数据;为拟合值, 且

因此

(11)

表8 仿真数据与经验公式数据

柱型装药水下爆炸远场压力场分布

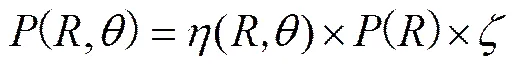
4 结论

为研究柱型装药水下爆炸压力场是否也存在类似球形场的经验公式, 文章定性分析了作用方位和长径比对柱型装药水下爆炸压力场的影响, 并得出以下结论。

1) 圆柱装药在极坐标(,)下存在点, 使得该点处柱型装药冲击波峰值等于球形装药, 该点在一定长径比范围内稳定于压力场50°附近处。

2) 基于数值仿真, 得出柱型装药与球形装药等效关系式, 结合Cole经验公式推导得出了柱型装药压力场分布公式均是较为准确的。

3) 随着长径比的增加, 轴向冲击波峰值压力减少, 径向峰值压力增加。柱形装药在径向(90°方向)产生的冲击波峰值压力大于等质量同位置的球形装药, 径向峰值压力最少提高了约4%, 根据此特点可以柱型装药长径比优化。

4) 在一定范围内, 随着长径比的增加, 装药形状对冲击波的影响距离增加, 冲击波传播形式仍有近似柱型传播变为球形传播。

文中所得柱型装药和球形装药远场爆炸压力场等效关系和柱型装药远场压力场计算公式, 已通过仿真初步验证其准确性, 后续的研究将侧重于通过试验进一步验证理论的正确性。

[1] Stemberg H M. Underwater Detonation of Pentolite Cylinders[J]. Physics of Fluids, 1995, 30(3): 761-769.

[2] Hammond L. Underwater Shock Wave Characteristics of Cylindrical Charges[R]. Defence Science and Technology Organisation. AMRL, DSTO-GD-0029, 1995.

[3] 侯俊亮, 蒋建伟, 门建兵, 等. 不同形状装药爆炸冲击波场及对靶板作用效应的数值模拟[J]. 北京理工大学学报, 2013, 33(6): 556-561.Hou Jun-liang, Jiang Jian-wei, Men Jian-bing, et al. Numerieal Simulation on Blast Wave Field and Deformation of Thin Plate Under Different-shape Charge Loading[J]. Transactions of Beijing Institute of Technology, 2013, 33(6): 556-561.

[4] 李金河, 赵继波, 池家春. 水中爆炸冲击波传播规律的实验研究[J]. 高能量密度物理, 2007, 22(4): 363-367.

[5] Cole R H. Underwater Explosions[M]. New Jersey: Princeton University Press, 1948．

[6] 贾宪振, 胡毅亭, 董明荣, 等. 基于ANSYS/LS-DYNA模拟水下爆炸冲击波的等效质量法[J]. 弹箭与制导学报, 2008, 28(3): 159-162.Jia Xian-Zhen, Hu Yi-ting, Dong Ming-rong, et al. Equivalent Mass Method of Underwater Explosionshock Wave Simulation Based on ANSYS/LS-DYNA[J]. Journal of Projectiles Rockets Missiles and Guidance, 2008, 28(3): 159-162.

[7] 肖秋平, 陈网桦, 贾宪振, 等. 基于AUTODYN的水下爆炸冲击波模拟研究[J]. 舰船科学技术, 2009, 31(2): 38-43.Xiao Qiu-ping, Chen Wang-hua, Jia Xian-zhen, et al. Numerical Study of Underwater Explosion Shock Wave Based on Autodyn[J]. Ship Science and Technology, 2009, 31(2): 38-43.

[8] 赵继波, 谭多望, 李金河, 等. 柱形装药水中爆炸近场径向压力测试初探[J]. 高压物理学报, 2008, 22(3): 323-328.Zhao Ji-bo, Tan Duo-wang, Li Jin-he, et al. Primary Research on Side Pressure of Cylindrical TNT at Underwater Exposive Close-Field[J]. Chinese Journal of High Pressure Physics, 2008, 22(3): 323-328.

[9] Li J, Rong J L. Experimental and Numerical Investigation of the Dynamic Response of Structuressubjected to Underwater Explosion[J]. European Journal of Mechanics B/Fluids, 2012, 32(3): 59-69.

[10] Zhang A-man, Yang W S, Huang C, et al. Numerical Sim- ulation of Column Charge Underwater Explosion Based on SPH and BEM combination[J]. Computers & Fluids, 2013, 71: 169-178.

(责任编辑: 杨力军)

Equivalent Relationship between Cylindrical Charge and Spherical Charge for Underwater Explosion

ZHANG Chi-yuGUO RuiLIU Rong-zhongCHEN LiangYANG Yong-liang

(School of Mechanical Engineering, Nanjing University of Science and Technology, Nanjing 210094, China)

Both cylindrical charge and spherical charge warheads are commonly used, so their underwater explosion performances attract more attention. However, the existing empirical formulas are only for spherical charge. To understand if the underwater explosion pressure field of cylindrical charge can be described by the empirical formulas for spherical charge, This paper qualitatively analyzes the influences of the orientation and the ratio of length to diameter on pressure field of cylinder charge underwater explosion, obtains a relationship expression of far field shock waves of cylinder charge and cycle charge by contrasting the pressure fields of cylindrical charge and same amount of spherical charge, and deduce an approximate empirical formula for cylinder charge by considering the empirical formulas for spherical charge. In addition, simulation is conducted to verify the accuracy of the deduced formula. This research may provide the basis for optimizing explosion performance of underwater warhead.

underwater explosion; cylindrical charge; spherical charge; empirical formula

10.11993/j.issn.1673-1948.2017.01.0013

TJ630; TQ560.1

A

1673-1948(2017)01-0065-06

2016-10-12;

2016-11-04.

高等学校博士学科点专项科研基金项目(20133219110019).

张弛宇(1991-), 男, 在读硕士, 主要研究方向为弹药精确化与智能化.