长征运载火箭制导方法

吕新广，宋征宇,2

(1. 北京航天自动控制研究所，北京 100854；2.宇航智能控制技术国防级重点实验室，北京 100854)

长征运载火箭制导方法

吕新广1，宋征宇1,2

(1. 北京航天自动控制研究所，北京 100854；2.宇航智能控制技术国防级重点实验室，北京 100854)

对长征系列运载火箭制导方法的发展和当前最新研究成果进行了综述。为满足轨道控制需求，制导方法起步于外干扰补偿制导，历经隐式和显式的摄动制导，逐步过渡到目前的闭环最优制导，并且发展出多个分支。传统迭代制导通过预测最佳入轨点、实时修正剩余飞行时间以及在线轨迹规划等技术，实现了高精度入轨控制；轨道预测修正迭代制导则通过跨飞行段取消位置与速度约束，并补偿对轨道的影响，实现了大推力直接入轨火箭的高精度控制；二次曲线直接制导通过改变程序角形式，增加控制维数，满足了终端姿态约束要求。最后结合我国未来重型运载火箭的任务特点，提出了在不同任务场景下采用统一的制导方法的设想，并以凸优化和联立法作为实现手段讨论了未来的研究重点。

运载火箭；制导方法；摄动制导；迭代制导；闭环最优制导

0 引 言

中国长征系列运载火箭家族目前已经具备大、中、小型多个火箭系列，覆盖从近地到深空各种类型轨道发射任务，更大运载能力的重型运载火箭也正在研制之中。在空间飞行任务的多样化发展过程中，制导方法承担了十分重要的角色。

制导方法用来控制运载火箭的质心运动轨迹。不论国外还是国内，制导方法都先后经历了从跟踪标准弹道到自主计算飞行轨迹的过程。美国土星五号火箭发射阿波罗飞船采用的迭代制导[1](Iterative guidance mode，IGM)是一个重要里程碑，首次将闭环最优制导方法应用于运载火箭，此后航天飞机所采用的动力显式制导[2](Powered explicit guidance，PEG)则是在其基础上进行的功能扩展；国内长期以来采用跟踪标准弹道的摄动制导，在交会对接任务中，长征二号F火箭首次采用迭代制导方法，取得了很高的入轨精度，以此为基础，根据任务需求制导方法又不断得到了改进；随着未来航天发射任务逐渐常态化和多样化，更高的控制精度、适应能力和自主性成为制导方法发展的主要方向。

本文对长征运载火箭制导方法的发展进行综述和展望。

1 早期制导方法

1.1外干扰补偿制导

我国最早的长征一号运载火箭仅配置分立的两个位置陀螺仪和三个加速度计，其制导方法被称作外干扰补偿制导[3-5]。该方法假设各种干扰所造成的偏差在小量范围内，从而可以将弹道参数进行线性化处理,并对最主要的影响因素进行干扰补偿。

以法向导引为例，引起法向速度与位置偏离标准弹道的关键因素在于俯仰姿态角与标准弹道程序角的偏差，以及对应时刻的纵向视加速度。为此将姿态角偏差信号与纵向视加速度信号合成后通过积分器，形成该干扰所产生的补偿量，加入到俯仰控制通道中。法向导引方程为：

(1)

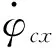
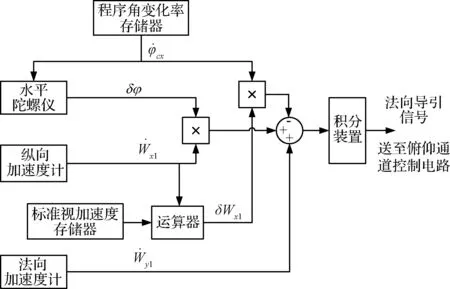
图1 法向导引功能实现示意图Fig.1 Illustration of normal guidance function

横向导引方程、关机方程的处理方式与之类似。该方法采用信息补偿代替显式的坐标转换和导航、制导计算，满足了当时所需的控制要求。

1.2隐式摄动制导

隐式摄动制导方法仅针对某些“特征量”进行较为简单的处理[4,6-7]。当三个加速度计安装在三轴稳定平台上时，其输出直接表征惯性坐标系“视速度”，利用“视速度”积分依次获得“视位置”、“视位置积分项”，并与标准弹道比较，通过反馈控制将飞行轨迹控制在标准弹道附近。这种方法无需较为复杂的引力计算过程，且视位置积分项在一定程度上反映了引力的影响，精度损失在可控的范围内。

以法向为例，隐式摄动导引方程形式如下：

(2)

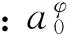
横向导引方程和隐式摄动关机方程也具有相似的形式。导引系数与关机系数的计算在地面完成，依据摄动理论将运动学方程在标准弹道附近泰勒展开，其中k1～k3采用被控量对速度的一阶偏导数，k4～k6采用对位置的一阶偏导数，k7～k9通过伴随函数线性逼近得到。

考虑到飞行弹道以及最终轨道都与速度、位置相关，而非视速度、视位置，当实际弹道偏离标准弹道以后，引力效应所产生的影响也偏离标准弹道，从而会引起控制精度的损失。为此,可在关机方程中增加对视速度三重积分项的反馈控制[8]。

1.3显式摄动制导

当箭上可以实时计算出速度、位置等导航参数时，制导方程也由“隐式”转为“显式”，即直接根据“物理量”进行控制。

在显式制导方程[9]中不再需要引入多重积分项，因为引力已考虑在导航参数中，导引方程如下：

(3)

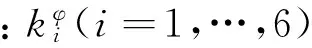
同样可直接计算物理量用于关机控制，例如采用绝对速度关机、轨道半长轴关机等。尽管如此，在弹道各个点上，速度、位置与标准弹道的差异仍是存在的，往往只能对某一特定被控参数有较高的控制精度，当入轨要求的轨道根数较多时，该方法从理论上难以兼顾多个指标。为此，工程应用中可通过分段和加权导引等方式实现对多个参数的控制，但其代价是制导精度的下降。在本世纪初的十几年中，所有在役的长征运载火箭均采用了显式的摄动制导方程。

2 闭环最优制导方法

2.1迭代制导的基本算法

迭代制导以最优控制原理为基础，通过解析公式在线计算到达目标轨道所需的速度增量、位置增量，并依此规划出最佳飞行程序角[10]。

摄动制导是对导航参数的组合进行控制，这只在干扰小的情况下等价于直接控制物理量。迭代制导则不再依靠标准弹道，用解析方式预测飞行终端条件，通过调整飞行轨迹使终端条件满足所有给定的入轨条件，而入轨条件直接对应了轨道根数。

为方便求解，将发动机最佳推力方向近似为时间的线性函数。制导方程如下形式：

(4)

若推力不可调节，在干扰下将难以在保证轨道精度的同时实现定点入轨，需通过迭代获得最佳入轨点。以当前状态为基础计算速度与位置的增量：

(5)

(6)

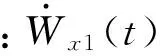
式中:g(tk)为引力在tk内对速度的影响；f(S)为利用目标轨道根数计算的飞行速度，是位置S的函数。

1)速度约束

（2）采取McCormack量表评分[3]评价患者的症状，主要包括腹部压痛或是反跳痛，子宫压痛、宫颈举摆痛、附件区压痛。各项0～3分，1分：有疼痛主诉，不过患者无肌紧张、面部表情变化；2分：疼痛多伴有肌紧张或者面部表情变化；3分：患者疼痛，十分痛苦。

从当前速度开始，在发动机推力和引力共同作用下达到目标速度，有：

(8)

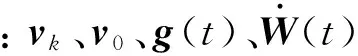
(9)

因此，对于发动机所产生速度增量的需求为：

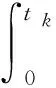
(10)

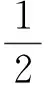
(11)

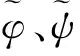
(12)

2)位置约束

上述入轨点计算考虑了飞行弧段的航程，即纵向位置是通过飞行时间tk来满足的。而法向和横向的终端位置则依靠式(4)中的(-k1+k2·t)和(-k3+k4·t)来保证，参数k1～k4应满足以下条件：

a)不对终端速度产生明显影响，近似满足下式：

(13)

(14)

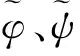
b)满足终端位置约束，即：

(15)

(16)

将式(13)～(16)联立,求解k1～k4解析解。

迭代制导通过规划全部剩余飞行时间内的姿态变化规律，来实现对多个变量的同时控制。在实际应用中，为提高入轨时刻火箭的稳定性，会提前停止迭代计算，因此产生少量的控制误差，最终误差的量级取决于停止迭代后的姿态跟踪误差。

以长征二号F运载火箭发射LEO轨道载人飞船为例，两种制导方法的误差对比见表1。

表1 LEO轨道制导方法误差Table 1 Guidance method error to LEO orbit

程序角仿真结果如图2所示。当干扰不大时，程序角近似为一条直线(临近入轨时的特殊处理除外)，见图中实线；而在实际飞行中，迭代制导为克服干扰影响而不断改变程序角，因此实际程序角不一定表现为直线，见图中虚线。

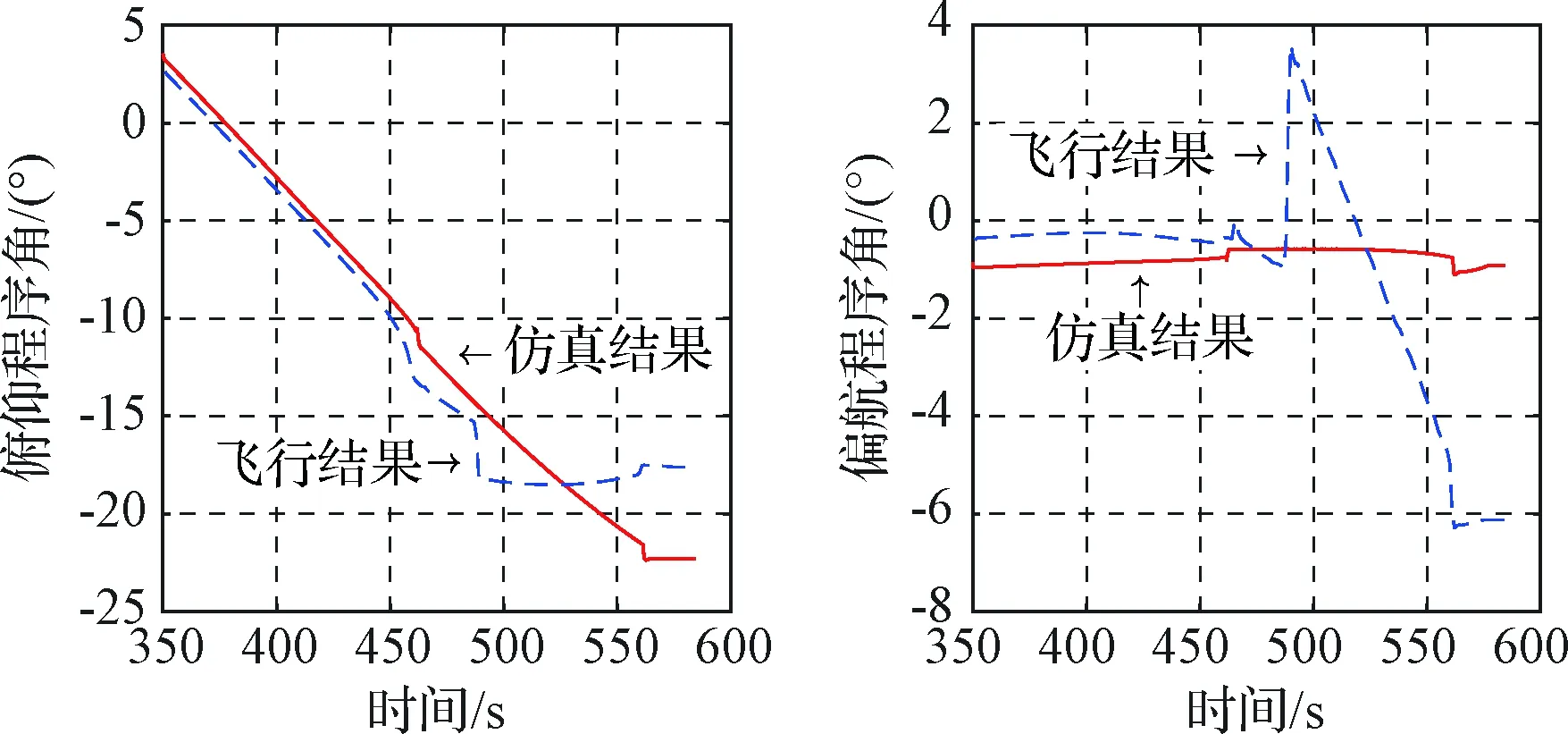
图2 仿真和实际飞行条件下的程序角Fig.2 The program angle under simulation and flight conditions

迭代制导对于动力系统的非致命故障也具有很好的适应性。图3中给出了在520 s推力下降50%之后的迭代参数与控制指令变化趋势。制导算法在敏感到加速度变化后，通过增加约60 s飞行时间及将入轨点真近点角向后推迟4°，最终准确入轨。

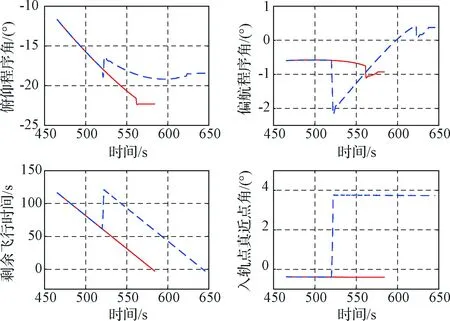
图3 推力减小50%时各种参数的变化Fig.3 Changes of parameters when thrust reduced by 50%

2.2轨道预测修正迭代制导

长征七号火箭二级为四台大推力发动机，总推力为72 t，未配置辅助动力系统或采用小推力入轨(如游动发动机等)，这与传统火箭有显著差异。在大推力直接入轨条件下，即使姿控系统保持原有的制导指令跟踪精度，其速度偏差也会成倍增加；而推力增大后系统干扰也会增大，使得保持原有跟踪精度也十分困难。上述因素均影响了入轨精度。

采用两两关机可以降低入轨前推力，但若两次关机间隔太久就会损失运载能力。在较短时间间隔内多增加一次关机过程，使得这期间推力变化剧烈(推力曲线见图4)，影响迭代参数估算的准确性，程序角大范围波动，进而产生较大的姿态跟踪误差。在此背景下，采用轨道预测修正的迭代制导方法。

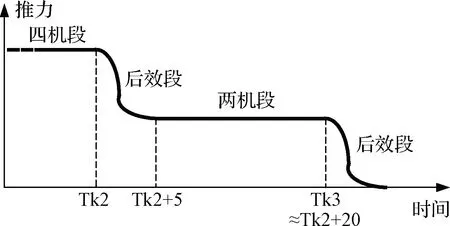
图4 入轨前发动机推力变化示意图Fig.4 Engine thrust curve before injection

针对程序角对位置变化较为敏感的特点，在第一次关机前先取消位置约束，仅保留速度约束。从图5可以看出，此时在推力突变50%的前后以及过程中，程序角变化范围仅为约0.5°，姿态跟踪稳定。但推力变化后入轨点位置也随之变化，迭代方程中因不再考虑位置约束而产生了位置误差，该误差属于系统性误差，可以对其进行补偿。

图5 入轨前程序角变化及跟踪效果Fig.5 Program angle and tracking effect before injection

补偿前先要进行误差的预测。根据火箭真空段的简化动力学模型：

(17)

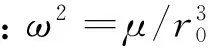
求得式(17)的解析解如下：

(18)

分别预测两台和四台发动机工作时的关机时间及对应的轨道根数，其偏差就是两两关机造成的误差。将上述偏差补偿到终端约束—即目标轨道根数中，可实现预测修正的目的。只有速度约束时程序角基本为常值，因此计算中用到的箭体姿态可选上周期计算出的程序角。

以CZ-7为例进行仿真，该方法取得了与传统制导方法相当的入轨精度(见表1)。

2.3考虑终端姿态约束的二次曲线直接制导

第2.1节和第2.2节介绍的迭代制导在干扰作用下其入轨姿态会呈现一定的散布。然而，很多有效载荷对星箭分离时的姿态是有要求的，若没有独立小喷管调姿系统，轨道精度与终端姿态两者难以兼得。在这种需求的牵引下，多种同时满足轨道和终端姿态约束的制导方法得到尝试，例如二次曲线直接制导方法，程序角形式为

(19)

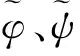
1)终端姿态约束

(20)

(21)

式中：φk、ψk为要求的入轨姿态。

2)终端速度约束，近似表达为

(22)

(23)

同样要求k1～k6为小量。

3)终端位置约束

(24)

(25)

将上述式(20)～(25)联立，求解k1～k6。

图6给出了典型干扰(以发动机推力线偏斜为例)下的程序角曲线。表2是两种制导方法入轨参数误差统计对比。

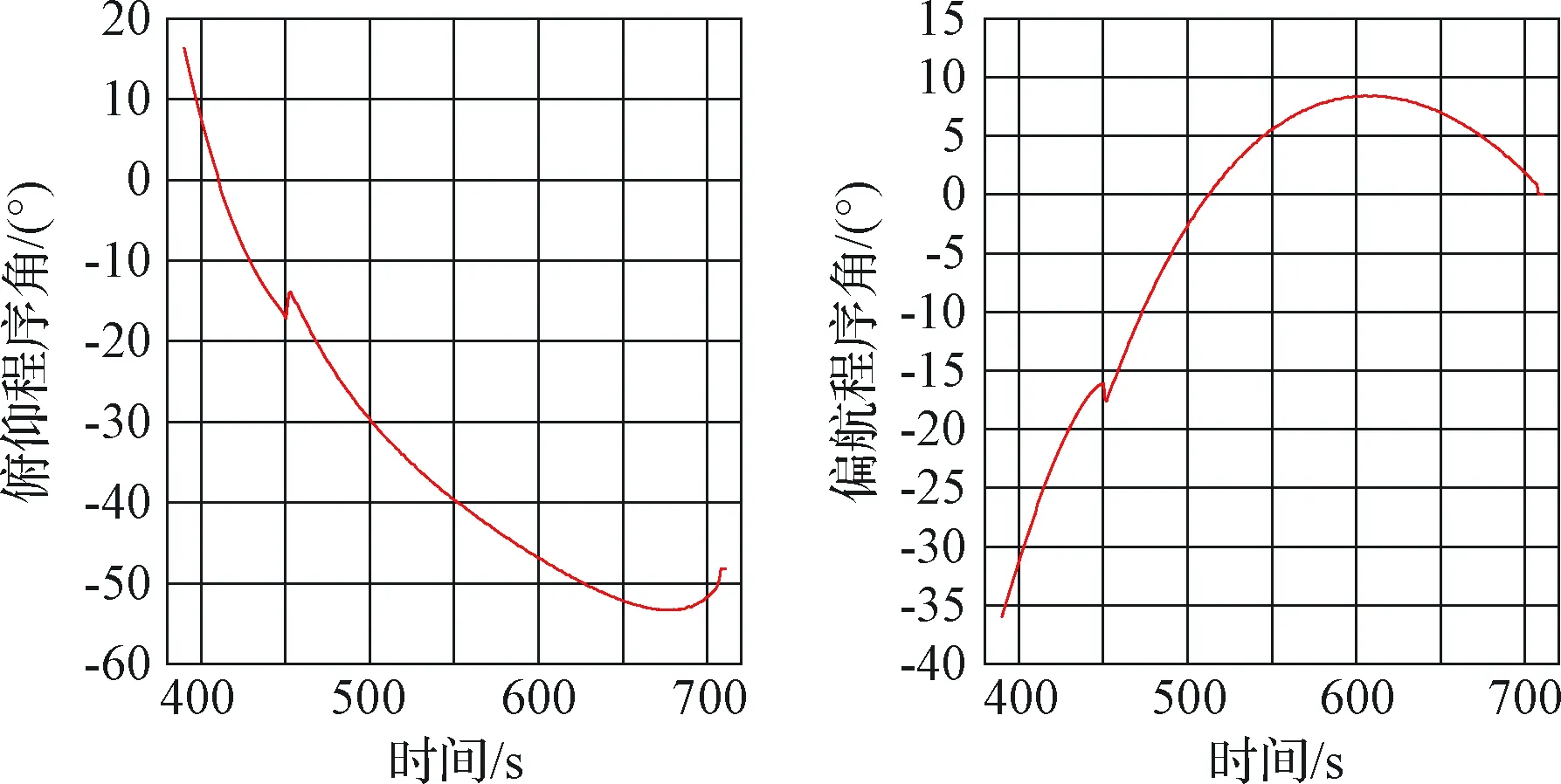
图6 典型干扰下程序角曲线Fig.6 The program angleunder typical interference

入轨参数偏差迭代制导二次曲线直接制导近地点高度偏差/km0.020.03近地点幅角偏差/(°)0.10.1轨道周期偏差/s0.20.2轨道倾角偏差/(°)0.0010.001升交点赤经偏差/(°)0.0030.003入轨俯仰角偏差/(°)20.10.3入轨偏航角偏差/(°)21.20.3

仿真表明，该方法能够达到所要求的轨道和终端姿态要求，在各种干扰下体现了很好的适应性。与此同时，考虑到k1～k6为小量的假设，终端姿态不能任意给定，该姿态应确保火箭入轨时推力方向与速度方向夹角不能太大，否则会产生方法误差。

3 未来重型运载火箭制导方法研究

3.1制导方法的发展趋势

重型运载火箭是世界各航天强国正在加大力度研制的新一代航天运输系统，它所面对的任务的复杂性决定了其必须具备自主应对各种飞行状况的能力，这在很大程度上为制导方法的发展指明了方向。

正在研制的美国SLS重型运载火箭，要求制导方法必须最大程度优化SLS的轨迹性能，甚至在故障下通过自主规划进入一个安全轨道等待救援。俄罗斯专家也认识到先进的制导方法能够提高任务可靠性，并针对某卫星发射失利的案例，提出用自适应制导方法，使得即使在基础级火箭未能正常入轨的情况下仍能将卫星送入轨道[11]。另一个值得关注的趋势是“端对端”的任务规划，即考虑从火箭起飞到飞行器进入最终轨道的全过程，不再采用预先序贯式分段的设计方法，强调全程整体优化。

综合上述需求，要求制导方法向着自主、在线和实时优化的方向发展，从而增大任务的适应性、可靠性和自主控制能力。

3.2重型运载火箭制导技术途径

对于包含大气层内飞行的运载火箭复杂控制问题，研究多集中于采用数值方法求解，如上升段采用多重打靶法[12]、经典差分法[13]、伪谱法[14]、凸优化方法[15-16]，下降着陆段采用伪谱法[17]、凸优化方法[18-19]等。

中国未来的重型运载火箭，其基础级用于上升段飞行，上面级用于轨道转移，而助推器将考虑回收利用，因此会同时面对三种相互关联的任务场景。对于此类问题能否采用一种统一的制导方法加以解决已经成为一个研究的方向，而凸优化或联立法[20-21]是目前考虑的两个主要技术途径。

无论上升段、转移段和着陆段，所有一般最优控制问题均能描述成如下形式：

minΦ(x(tf))

s.t.

式中:Φ(x(tf))是目标函数；p∈Rnp是模型参数；f为微分方程组的右边约束，可以认为是运载器的动力学方程；x(t)∈Rnx为状态变量，通常采用速度、位置、姿态作为状态变量；x0∈Rnx为状态变量的初始值，对于实时控制则为当前值。

其他量的设置与具体应用场景有关，本文假设火箭上升段采用推力大小可调节的摇摆发动机控制，轨道转移段采用固定推力轨控发动机和姿控喷管控制，再入返回段采用摇摆发动机和栅格舵控制，则各个物理量的含义如下：

u(t)∈Rnu为控制变量。对于上升段，u为推力大小和方向；在轨道转移段，u用于控制轨控发动机和姿控喷管的开启与关闭；再入返回段，u为推力大小和方向、栅格舵摆角等。

N1(x(tf))为终端目标集约束。对于上升段和轨道转移段，一般为轨道根数、箭体姿态、角速率等；而对于再入返回段，则要求位置到达预定着陆点，速度接近为0，姿态为垂直着陆姿态等。

gE为过程等式约束，gI为过程不等式约束，用来定义状态变量和控制变量的边界约束。例如，程序角速率约束、飞出发射塔架前姿态垂直的约束、子级落点约束、发动机推力上下限和最大摆角限制等。轨道转移段和再入返回段同样具有类似的约束。

凸优化与联立法均能解决式(26)的一般性最优控制问题。但在许多情况下约束条件是“非凸”的，因此凸化转换是凸优化的重点；而对于联立法而言，在增强收敛性和计算效率方面仍有许多工作亟待开展。限于篇幅上述内容不再展开。

4 结 论

本文回顾了中国长征运载火箭上升段飞行中制导方法的发展，并探讨了未来重型运载火箭制导方法拟采取的技术途径。

自中国载人交会对接任务起，长征运载火箭开始采用闭环最优制导方法，并针对大推力直接入轨以及终端姿态约束需求，对制导方法进行了不断的改进和完善。随着未来任务对控制系统能力需求的不断提高，全程优化和自主控制逐渐成为发展方向，也使得制导方法面临新挑战：解决复杂约束下的在线实时轨迹规划和控制难题。这一问题的解决将为未来的自主飞行控制打下基础。

[1] Chandler D C,Simith I E. Development of the iterative guidance mode with its application to various vehicles and missions[J]. Journal of Spacecraft and Rockets, 1967,4(7): 898-903.

[2] Mchenry R L, Long A D, Cockrell B F, et al. The space shuttle ascent guidance and control [J]. Journal of the Astronautical Sciences,1979, 27(1):1-38.

[3] 胡德风. 导弹与运载火箭制导系统回顾与发展方向设想[J]. 导弹与航天运载技术, 2002(5):44-48. [Hu De-feng. Development and review of guidance system in missile and launch vehicle[J]. Missiles and Space Vehicles, 2002(5):44-48.]

[4] 徐延万. 控制系统(上)[M]. 北京: 中国宇航出版社, 1989: 252-308.

[5] 韩厚健. 长征系列运载火箭介绍：长征一号系列(二) [J].中国航天,1997(6):9-11. [Han Hou-jian. Long march series launch vehicle introduction: LM-1 series(2) [J]. Aerospace China, 1997(6):9-11.]

[6] 邸乃庸,朱维增,吴瑞华. 长征系列运载火箭介绍：长征二号系列(三) [J]. 中国航天,1997(10):14-20. [Di Nai-yong, Zhu Wei-zeng, Wu Rui-hua. Long march series launch vehicle introduction: LM-2 series(3) [J]. Aerospace China, 1997(10):14-20.]

[7] 陈国华. 长征系列运载火箭介绍：长征三号系列(四) [J]. 中国航天,1998(6):15-19. [Chen Guo-hua. Long march series launch vehicle introduction: LM-3 series(4) [J]. Aerospace China, 1998(6):15-19.]

[8] 徐信华,邵载民,陈百初,等. 长征四号运载火箭制导、姿控和轨道测量系统[J]. 宇航学报, 1989, 10(4):3-9. [Xu Xin-hua, Shao Zai-min, Chen Bai-chu, et al. LM- 4 guidance, attitude control and trajectory measurement system [J]. Journal of Astronautics, 1989, 10(4):3-9.]

[9] 崔鑫水. CZ-2E运载火箭制导技术[J]. 导弹与航天运载技术,1993(2):21-27. [Cui Xin-shui. Guidance technique of CZ-2E launch vehicle [J]. Missiles and Space Vehicles, 1993(2):21-27.]

[10] 宋征宇. 从准确、精确到精益求精—载人航天推动运载火箭制导方法的发展[J]. 航天控制,2013,31(1):4-10. [Song Zheng-yu. From accurate, precise to perfect-manned space promotes the development of guidance method on launch vehicle[J]. Aerospace Control, 2013, 31(1):4-10. ]

[11] Yanova O V, Akobian B G. Launcher mission risk reduction due to the advanced adaptive guidance algorithms[C]. The 67th International Astronautical Congress (IAC), Guadalajara, Mexico, September 26-30, 2016.

[12] Lu P, Pan B. Highly constrained optimal launch ascent guidance[J]. Journal of Guidance, Control, and Dynamics, 2010, 33(2): 404-414.

[13] Lu P, Sun H, Tsai B. Closed-loop endoatmospheric ascent guidance[J]. Journal of Guidance, Control, and Dynamics, 2003, 26(2): 283-294.

[14] 张志国,余梦伦,耿光友,等. 应用伪谱法的运载火箭在线制导方法研究[J]. 宇航学报, 2017,38(3):262-269. [Zhang Zhi-guo, Yu Meng-lun, Geng Guang-you, et al. Research on application of pseudo-spectral method in online guidance method for a launch vehicle [J]. Journal of Astronautics, 2017, 38(3):262-269.]

[15] Harris M W, Acikmese B. Lossless convexification of non-convex optimal control problems for state constrained linear systems[J]. Automatica, 2014, 50(9): 2304-2311.

[16] Liu X, Lu P. Solving nonconvex optimal control problems by convex optimization[J]. Journal of Guidance, Control, and Dynamics, 2014,37(3):750-765.

[17] Ross I M, Fahroo F. Pseudospectral methods for optimal motion planning of differentially flat systems[J]. IEEE Transactions on Automatic Control, 2004, 49(8): 1410-1413.

[18] Zhao D J, Song Z Y. Reentry trajectory optimization with waypoint and no-fly zone constraints using multiphase convex programming [J]. Acta Astronautica, 2017, 137(8): 60-69.

[19] Scharf D P, Acikmese B, Dueri D, et al. Implementation and experimental demonstration of onboard powered-descent guidance[J]. Journal of Guidance, Control, and Dynamics, 2016, 39(1): 1-17.

[20] 邱丰, 宋征宇. 采用联立法求解大姿态约束的上升段轨迹优化问题[J]. 宇航学报, 2017,38(1):26-33. [Qiu Feng, Song Zheng-yu. Large terminal attitude constrained trajectory optimization of ascent stage via simultaneous method[J]. Journal of Astronautics, 2017, 38(1):26-33.]

[21] Ma L, Shao Z J, Chen W F, et al. Trajectory optimization for lunar landing with a Hamiltonian-based adaptive mesh refinement strategy [J]. Advances in Engineering Software, 2016, 100(10): 266-276.

GuidanceMethodsofLong-MarchLaunchVehicles

LV Xin-guang1, SONG Zheng-yu1,2

(1. Beijing Aerospace Automatic Control Institute, Beijing 100854, China;2. National key Laboratory on Aerospace Intelligent Control, Beijing 100854, China)

The development of the guidance methods of the Long-March launch vehicles and the latest research results are reviewed. In order to meet the orbit requirements of the payloads, the guidance methods started from the disturbance compensation guidance, followed by the implicit and explicit perturbation guidance, and then the current closed-loop optimal guidance developing many branches. The traditional iterative guidance achieves high-precision orbit by predicting the optimal injection point, real-time correction of the time-to-go and on-line trajectory planning. The iterative guidance with orbit prediction and correction is designed to meet the requirements of the large thrust direct injection, relaxing the position and velocity constraints in different phases, and the errors caused by this way are predicted and compensated. The quadratic function guidance increases the number of the control dimensions by changing the form of the program angle to meet the requirements of the terminal attitude constraints. Finally, according to the characteristics of the Chinese heavy-lift launch vehicles, the idea of a unified guidance method for various scenarios in the future is proposed, and the research emphases, such as convex optimization and simultaneous method, are discussed as the effective means.

Launch vehicle; Guidance method; Perturbation guidance; Iterative guidance; Closed-loop optimal guidance

V448

A

1000-1328(2017)09- 0895- 08

10.3873/j.issn.1000-1328.2017.09.001

2017- 04- 05;

2017- 07- 07

吕新广(1978-)，男，研究员，硕士，主要从事飞行器导航与制导技术研究。

通信地址：北京142信箱402分箱(100854)

电话：(010)68389054

E-mail: lv_xg@163.com

宋征宇(1970-)，男，博士生导师,主要从事飞行器控制、制导与仿真，智能自主控制技术等研究。本文通信作者。

通信地址：北京142信箱402分箱(100854)

电话：(010)68389311

E-mail: zycalt12@sina.com