一种结合项目属性的混合推荐算法①
2017-10-13陈庚午王爱玲
于 波, 陈庚午,2, 王爱玲,2, 林 川,2
一种结合项目属性的混合推荐算法①
于 波1, 陈庚午1,2, 王爱玲1,2, 林 川1,2
1(中国科学院沈阳计算技术研究所, 沈阳 110168)2(中国科学院大学, 北京 100049)
传统的协同过滤推荐算法中仅仅根据评分矩阵进行推荐, 由于矩阵的稀疏性, 存在推荐质量不高的问题. 本文提出了一种结合项目属性相似性的混合推荐算法, 该算法通过计算项目之间属性的相似性, 并且与基于项目的协同过滤算法中的相似性动态结合, 通过加权因子的变化控制两种相似性的比重来改善协同过滤中的稀疏性问题, 并且将综合预测评分和基于用户的协同过滤预测评分相结合来提高推荐质量, 最终根据综合评分来进行推荐. 通过实验数据实验证明, 该算法解决了协同过滤算法的矩阵稀疏性问题.
协同过滤; 混合算法; 综合相似性; 稀疏性; 项目属性
目前, 个性化推荐技术[1]是解决信息过载的主要的有效手段, 它根据分析用户的历史行为信息, 在海量信息中运用推荐算法自动快速的发现符合用户个人兴趣的服务和内容, 推荐算法作为个性化推荐技术的核心部分起到了重要作用, 其中协同过滤算法得到了广泛地应用.
协同过滤算法[2-5]的基本原理是通过对用户历史行为数据的挖掘发现用户的偏好, 基于不同的偏好对用户进行群组划分并推荐品味相似的商品. 根据协同过滤的相关特征, 协同过滤算法分成基于用户的协同过滤算法和基于项目的协同过滤算法. 基于用户的协同过滤首先计算活动用户和其他用户之间的相似度, 并从相似用户的兴趣为目标用户进行推荐. 基于项目的协同过滤基于这样的假设: 能够引起用户兴趣的项, 必定与之前评分高的项相似.
本实验室新媒体广播项目主要是为沈阳广播电台, 烟台广播电台和长春广播电台提供新媒体广播服务, 旨在将电台广播与互联网结合, 打造包括后台服务、主持人端、导播端和移动端的一体化新媒体广播服务平台. 在移动端和主持人端的交互过程中发现, 服务平台于广播栏目的个性化推荐依然一种有效的推荐措施. 由于栏目的收听和互动存在很强的时间聚集性,所以由此衍生的评分矩阵具有很强的稀疏性. 而且在协同过滤推荐算法中, 数据稀疏性问题是影响协同过滤系统推荐质量的一个关键原因, 由于评分矩阵的稀疏, 导致用户相似性度计算的评分向量中共同评分项太少, 使得相似性的度量误差变大, 最近邻居搜寻的结果的准确性也就会变得难以保证, 最终进行评分预测时就会使最终的预测值和真实评分值之间产生较大的误差, 从而影响推荐的准确度. 针对于此问题, 本文提出一种基于内容过滤和协同过滤相结合的混合模式推荐技术[6,7], 将基于项目属性的相似性和协同过滤中基于项目的相似性结合, 提出一种新的相似性度量方法, 解决协同过滤中的矩阵稀疏问题.
1 相关工作
在大部分的推荐系统当中, 用户对于项目的评分是非常有限的. 比如在视频推荐的系统中, 视频的数目数以十万计, 然而用户参与评价的视频最多至几十部, 再次基础上的评分数据相当稀疏, 由此产生的评分向量并不能准确的计算用户之间的相似性. 由此协同过滤的推荐质量大大下降.
协同过滤中矩阵稀疏性问题一直是人们研究的重点, 在众多解决方法中, 最为简单的办法就是为用户未评分的项目设定一个固定的缺省值, 一般将缺少的评分设定为整个评分范围的中间值, 例如评分范围为1~5分制时将评分设定为3分. 这种改进措施在一定程度上可以提高协同过滤的推荐准确度但是添加的缺省值并不能准确的表示实际评分情况, 所以此方法不能从根本上解决稀疏性带来的问题. 目前很多学者也提出了可以有效解决协同过滤稀疏性的方法, 比较成功的主要有大类: 一种是通过数学原理降低矩阵的稀疏性, 通过奇异值分解技术平滑输入矩阵, 降低矩阵的维数从而降低矩阵的稀疏性. 但是分解技术算法时间复杂度较高, 并且降低维数往往会导致评分矩阵中信息的丢失, 在评分极度稀疏的情况下, 效果并不理想. 另一种解决方法是通过融合推荐算法来解决协同过滤中矩阵稀疏性的问题, 在协同过滤的计算过程中加入内容的预测等. 本文即选择了混合算法的策略, 提出了结合属性相似性的协同过滤中的项目相似性的混合推荐算法.
2 算法相关理论
2.1 评分矩阵
推荐系统包含M个用户和N个项目, 它们形成了一个 M×N的矩阵列表, 此列表即为用户-项目评分矩阵, 矩阵中的值R表示用户对项目的评分, 其中评分的值设置为0-5之间的整数, 如果R=0则表示用户没有对项目评分, 评分值越高表示用户对项目喜爱程度越高.
2.2 相似度的计算方法
协同过滤算法中, 传统的3种相似性度量方法分别为余弦相似性, 相关相似性和修正余弦相似性[8]. 本文采用修正余弦相似性计算方法. 在评分矩阵中, 每一个项目或者用户都对应一个有评分构成的评分向量, 所以在基于用户的协同过滤算法中, 用户U和用户U的相似性计算公式如下所示:
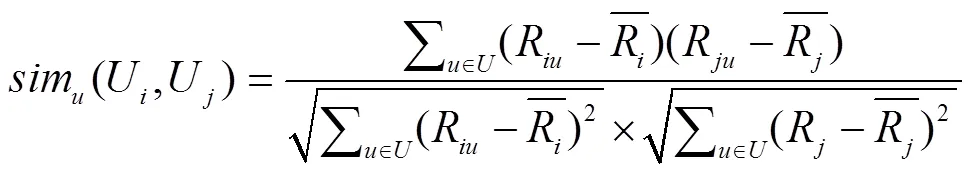
表示用户U和U共同评分集合,表示平均评分.
和用户的相似性计算类似, 在基于项目的协同过滤算法中, 项目V和V的相似性计算如下所示:

3 结合项目属性相似的协同过滤研究
3.1 内容预测的原理
基于内容的推荐算法来源于信息检索领域, 其基本原理根据项目的属性特征构建项目的属性特征文件, 然后通过项目的特征属性文件与用户的兴趣爱好进行相似性匹配, 将用户感兴趣的项目推荐给用户. 内容过滤的推荐技术仅仅考虑项目的属性特征并不需要考虑到用户的评价行为, 因此内容的预测不会受到用户评分稀疏性的影响. 在此基础上本节对协同过滤中加入项目属性特征相似性进行了研究.
3.2 项目属性相似性的计算
在协同过滤推荐算法中, 由于相似性是根据评分矩阵计算, 然而一些项目没有足够的评价, 所以由稀疏矩阵产生的评分向量并不能有效的计算项目之间的相似性[9]. 但是一般的协同过滤推荐系统会有对项目的简单描述, 比如在广播节目有栏目, 话题, 微博等类别属性, 而栏目又具有生活, 医疗, 娱乐, 音乐, 交通等属性. 这些栏目的属性, 可以看成是有关项目的关键词, 这样, 每个项目Itemi就可以由关键词来描述, 如下:
Itemi={A1, A2, …, An}
则通过分析项目信息就可以得到项目-属性矩阵; 假设Item个数为n, 属性的个数是k, 则项目-属性矩阵如表1所示.
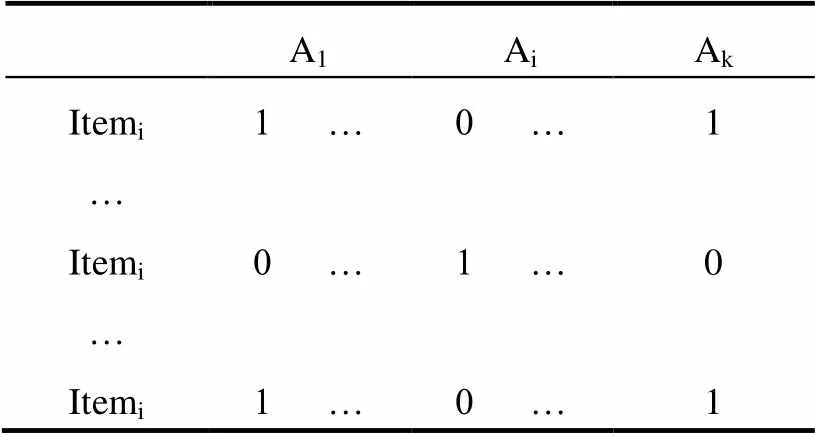
表1 项目-属性表
其中, 1表示项目拥有属性, 0表示没有此属性.
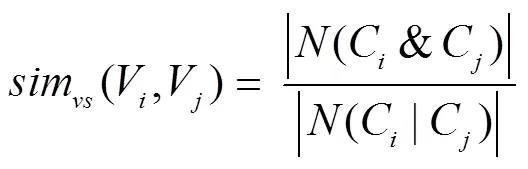
其中项目C和C表示项目V和项目V的属性向量,表示结果向量中1的个数.
3.3 综合相似性的计算
协同过滤的推荐效果一般要优于内容过滤[9], 因此, 在推荐过程中主要还是依赖协同过滤, 但是由于在评分矩阵极端稀疏的情况下, 对两个项目进行评分的用户集合可能很小. 如果只有一两个用户对项目共同评分, 即使算出的相似度较高其可信度也是较低的. 所以, 在基于项目的协同过滤中, 根据评分计算项目相似性的同时加入属性的相似性, 将两种相似行进行线性组合, 最终得到项目的综合相似性.
在协同过滤算法中, 基于项目的基本原理是根据所有用户对项目的偏好, 发现项目和项目之间的相似度, 即假设能够引起使用者兴趣的物品, 必定与其之前偏好的物品相似, 通过计算物品间的相关来做推荐[10]. 其原理如图1所示.
如图所示, 物品a同时被用户a和用户b喜欢, 物品c也同时被用户a和用户b喜欢, 因此可以认为物品a和物品c具有相似性, 同时用户c喜欢物品a, 所以可以将与物品a具有相似性的物品c推荐给用户.
根据上述原理, 通过评分矩阵提取出两个项目的评分向量, 则通过基于项目的相似性计算公式即公式(2)可以得到两个项目之间的相似性.

图1 协同过滤原理图
为了提高质量, 本文将两种相似性进行线性组合, 引入权值变量λ, 由于基于评分的相似性与两个项目的共同评分用户的数量有关, 共同评分用户越多相似性越准确, 所以权值变量λ的计算公式如下:

(5)
如公式所示, λ和两个项目的共同评分用户数目息息相关, 如果两个项目的共同评分用户数目越多, 则基于评分的项目相似性所占的比重越大, 从而使相似度计算更加准确.
通过分析公式(5)可知, 如果存在冷启动项目, 即没有用户进行评价, 则λ的值为0, 此时可以根据项目本身的相似性计算得到其相似项目集合来预测评分. 如果存在评分矩阵极度稀疏的情况, 同样λ的值会相应的减小, 根据评分计算的相似性比重也较少, 所以可以减少稀疏性对于相似性计算的影响, 由此可知, 综合相似性的计算可以在一定程度上解决推荐算法中的矩阵稀疏性问题.
3.4 综合评分的预测
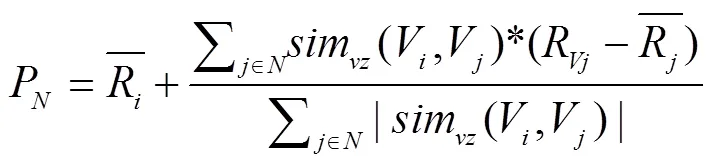
由上述可知, 由综合相似性得到的评分P仅仅是根据项目之间的相似性计算而来, 而忽略了用户之间的相似性对于推荐算法的影响, 因此, 在得到项目之间的相似性的同时, 本文引入协同过滤中基于用户的相似性计算. 在协同过滤中, 与计算项目相似性类似, 通过评分矩阵可以得到每个用户的评分向量, 则通过公式(1)可以得到用户之间的相似性, 由次引入基于用户的协同过滤预测评分, 其计算公式如下:
(7)
在得到根据项目相似性计算的预测评分P和根据用户之间的相似性计算的预测评分P之后, 通过权值因子将两个评分线性组合, 通过实验来确定的值, 最终得到综合预测评分来进行推荐. 其组合公式如下:

其中为权重因子,∈[0,1].
3.5 推荐过程
为了解决协同过滤中冷启动和稀疏性的问题, 本文引入了基于项目本身属性相似性的计算, 将项目属性相似和基于项目的协同过滤相似性线性结合, 然后将混合预测评分与基于用户的协同过滤评分动态结合, 最终的到综合预测评分. 其推荐过程如图2所示.
推荐过程描述如下:
Step1: 根据公式(3)计算项目之间基于属性的相似度.
Step2: 根据公式(2)计算项目之间基于评分的相似度.
Step3: 根据公式(5)计算项目之间的综合相似度:.
Step4: 根据公式(6)计算基于项目综合相似性的预测评分P.
Step5: 根据公式(7)计算基于用户相似性的预测评分PU.
Step6: 根据公式(8)计算最终综合预测评分P.
Step7: 根据综合评分P对项目进行降序排序, 将集合的top—k推荐给用户.
4 实验结果及分析
4.1 实验数据
本文采用本实验室统计的用户与栏目交互的实际数据, 用户与栏目的互动行为包含收藏, 点赞, 评论, 阅读, 和收听五个行为, 根据用户的行为为栏目打分, 其中收藏2分, 点赞, 评论分别1分, 阅读收听分别0.5分由此可得到用户和栏目的评分矩阵. 根据实验室得到的数据经过处理可以得到1000个用户对97个栏目10000条评分记录, 评分范围为1~5. 数值越高表示用户对栏目的偏爱程度越高, 本文将数据集按照80%的训练集和20%的测试集划分. 同时每部栏目都有其所属的类别, 本文将栏目分成以下类别: 生活, 医疗, 音乐, 交通, 新闻, 教育, 谈话, 服务, 戏剧, 综艺. 然后将这10种类别作为栏目的属性, 用于获得栏目的属性相似度.
4.2 度量标准
推荐系统常用的度量标准有平均绝对偏差MAE和均方根误差RMSE. 本文采用平均绝对偏差MAE作为度量标准, MAE用于度量推荐算法的估计评分与真实值之间的差异. MAE值越小, 估计的准确性越高,定义如下:

其中P为用户对项目的预测评分,r为用户对项目的真是实际评分,为测试集中记录评分的个数.
4.3 实验结果
实验一: 确定权重因子.
取项目和用户的最近邻居数目都为30做实验, 通过改变权重因子值观测MAE的变化. 其中的值以0.1为步长从0.2变化到0.8. 混合推荐算法的平均绝对误差MAE如图3所示.
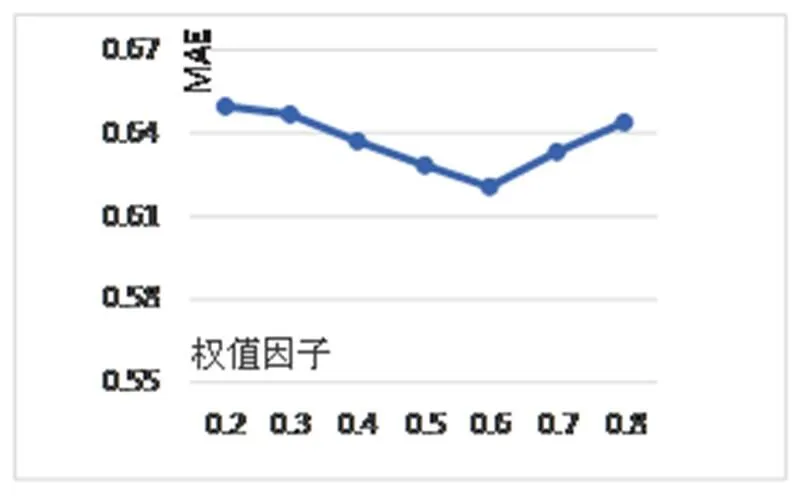
图3 实验一结果
从图3可以看出, 当α的值取值太大或太小推荐效果并不是最好, 当α=0.6时MAE的值最小, 意味着推荐质量最好. 因此取α=0.6进行实验二, 来确定最近邻居数并比较两种算法的优劣.
实验二: 比较混合算法与协同过滤的优劣.
由实验一确定α后, 通过改变最近邻居数目来观察MAE值的变化, 同时与基于用户的协同过滤作推荐结果比较如图4所示.
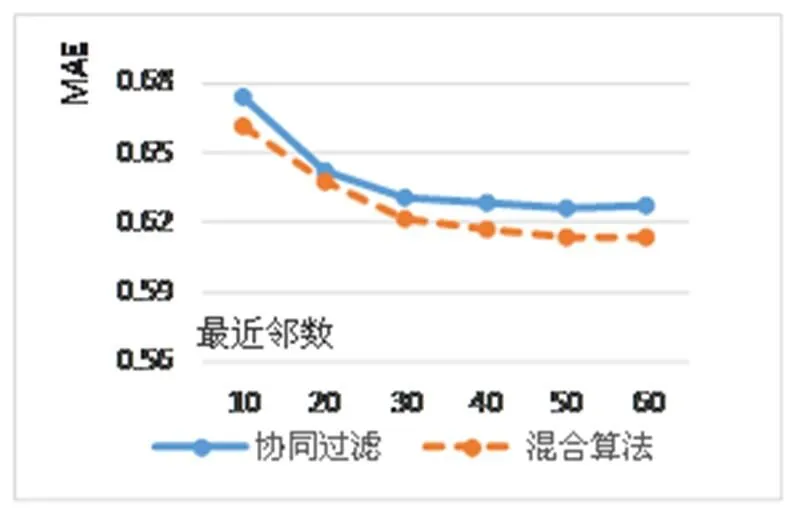
图4 实验二结果
从图4可以看出, 当最近邻居数目为50的时候推荐效果比较好, 而且通过两个曲线比较可以看出, 混合算法的MAE相对于协同过滤算法有明显的减小, 所以改进的推荐混合推荐算法具有比较好的准确性和比较好的推荐效果.
实验三: 稀疏性比较
在通过实验一和实验二确定了α和最近邻居的数目后, 此实验通过改变评分矩阵的稀疏性来比较协同过滤和混合算法的优劣. 由实验室的数据可以计算的当前数据集合的稀疏等级为1-10000/(97*1000)=0.89. 为此通过删除评分数据来增加矩阵的稀疏等级, 删除的策略为优先删除参与评分用户数目较少的项目的数据, 即优先删除冷门栏目, 由此矩阵的评分更加稀疏. 分别选择稀疏程度在0.89, 0.92, 0.95, 0.98数据集合进行试验结果如图5.

图5 稀疏性比较
由实验结果可知, 传统的协同过滤在矩阵稀疏的情况下推荐质量会大大的减少, 而本文提出的混合推荐算法, 虽然随着矩阵的稀疏增加推荐准确度也有所下降, 但是相对于协同过滤算法具有明显的优势. 因此混合推荐算法在降低了矩阵稀疏对于推荐结果的影响.
5 结语
本文对传统推荐算法进行了优化, 增加权值因子来组合项目属性相似性和协同过滤的相似性, 得到的相似性度量方法使得计算的项目的最近邻居更加准确. 实验结果表明, 本文提出的算法显著提高了协同过滤推荐算法的推荐质量, 并且可以有效解决评分矩阵稀疏性的问题. 实验不足之处是在解决用户冷启动问题上, 计算精度还有待提高, 需要进一步的深入研究.
1 冷亚军,陆青,梁昌勇.协同过滤推荐技术综述.模式识别与人工智能,2014,8:720–734.
2 杨博,赵鹏飞.推荐算法综述.山西大学学报(自然科学版),2011,3:337–350.
3 刘青文.基于协同过滤的推荐算法研究[博士学位论文].合肥:中国科学技术大学,2013.
4 孔维梁.协同过滤推荐系统关键问题研究[博士学位论文].武汉:华中师范大学,2013.
5 Peng H. Research of collaborative filtering recommendation algorithm based on network structure. Journal of Networks, 2013: 810.
6 Gong S. A collaborative filtering recommendation algorithm based on user clustering and item clustering. Journal of Software, 2010, 5(7): 745–752.
7 张驰,陈刚,王慧敏.基于混合推荐技术的推荐模型.计算机工程,2010,22:248–250,253.
8 张旭阳.基于权重的混合推荐策略研究[硕士学位论文].昆明:云南大学,2015.
9 张腾季.个性化混合推荐算法的研究[硕士学位论文].杭州:浙江大学,2013.
10 高虎明,赵凤跃.一种融合协同过滤和内容过滤的混合推荐方法.现代图书情报技术,2015,6:20–26.
Hybrid Recommendation Algorithm Combined with the Project Properties
YU Bo1, CHEN Geng-Wu1,2, WANG Ai-Ling1,2, LIN Chuan1,2
1(Shenyang Institute of Computing Technology, Chinese Academy of Sciences, Shenyang 110168, China)2( University of Chinese Academy of Sciences, Beijing 100049, China)
Traditional collaborative filtering recommendation algorithm only bases on matrix. Due to the sparsity of matrix, the quality of recommendation is not high. This paper proposes a hybrid recommendation algorithm whose similarity is combined with the properties of projects. This algorithm improves the data sparseness in collaborative filtering through the change of the weighted factor, controlling the proportion of two kinds of similarity that one is the similarity of attribute between projects and the other is the similarity of item-based collaborative filtering algorithm. And the comprehensive prediction score and user-based collaborative filtering prediction score are combined to improve the quality of recommendation. Finally, the recommendation is given according to the comprehensive scores. Experiments show that the algorithm has better recommendation quality.
collaborative filtering; hybrid algorithm; comprehensive similarity; sparse matrix; project properties
2016-04-06;收到修改稿时间:2016-04-27
[10.15888/j.cnki.csa.005490]
