基于放电脉冲波形匹配的局部放电类型识别
2017-10-12孟庆振杨金伟徐学伟韩宝国李静鹏
孟庆振+杨金伟+徐学伟+韩宝国+李静鹏


摘 要: 针对局部放电类型识别中不易全面提取特征等问题,提出将采集到的局部放电脉冲信息与经典的局部放电类型信息直接进行波形相识度匹配的方法,该方法只需通过表征波形相似性的互近似熵值便可识别出局部放电类型。首先讨论不同局部放电类脉冲所具有的不同分布特点和样式,归纳分析五种典型局部放电的脉冲波形。具体研究基于互近似熵进行局部放电信号识别的原理方法、识别系统和实现流程。实验结果证实了基于互近似熵的局部放电识别方法的准确性和高效性。
关键词: 局部放电; 放电脉冲; 波形匹配; 互近似熵
中图分类号: TN98?34; TM76 文献标识码: A 文章编号: 1004?373X(2017)19?0164?05
Partial discharge type identification method based on discharge pulse waveform matching
MENG Qingzhen, YANG Jinwei, XU Xuewei, HAN Baoguo, LI Jingpeng
(Linyi Power Supply Company, State Grid Shandong Electric Power Company, Linyi 276023, China)
Abstract: It is difficult to fully extract the features in partial discharge type identification, so a method to march the waveform similarity between the sampled partial discharge pulse information and classical partial discharge type information directly, which can recognize the partial discharge type by means of the cross?approximate entropy presenting the waveform similarity. In this paper, the different distribution characteristics and styles of various partial discharge type pulses are discussed, and five pulse waveforms of classical partial discharge are summarized. The principle method, identification system and implementation procedure for partial discharge signal identification based on cross?approximate entropy are studied. The experimental result proves that the partial discharge type identification method based on cross?approximate entropy is accurate and effective.
Keywords: partial discharge; discharge pulse; waveform matching; cross?approximate entropy
0 引 言
尽管GIS(Gas Insulated Switchgear)设备具有高可靠性、无需频繁检修等优点而得到广泛应用,但由于GIS设备一旦出现故障将可能导致整个电力系统严重故障。因此,及时发现GIS设备可能潜在的故障和各种异常情况,以保障GIS设备可靠运行具有重要意义[1]。
从GIS设备运行统计数据发现,GIS设备故障中包括绝缘故障(57.3%)、机械故障(18.1%)和气体泄漏故障(12.4%)[2]。由此可见,绝缘故障成为影响GIS可靠运行的主要因素。GIS设备绝缘性能下降甚至发生闪络故障可通过局部放电进行检测。作为一种有效的局部放电检测手段,特高频法利用局部放电时产生很陡的脉冲电流,通过采集局部放电辐射出的300~3 000 MHz频段的电磁波信号进行局部放电的检测,已逐步应用于GIS设备的局部放电信号采集和状态评估中。
由于局部放电是一个很复杂的物理电气过程,受缺陷类型、放电程度、缺陷位置、现场环境等诸多因素的影响,所呈现的特征具有分化性的特点,不容易识别,而且局部放电信号容易被电力现场的电磁干扰所淹没,增加了局部放电信号的识别难度。
当前局部放电信号进行放电模式识别方法主要针对局部放电信号的脉冲分布特征展开研究,进而提取特定的特征量,通过支持向量机算法、统计概率分类法、距离分类法、核主分量分析方法、模糊识别、专家系统、神经网络等方法进行放电模式识别[3?6],取得了一定的效果。由于局部放电现场情况复杂导致特征的多样化,要准确捕捉局部放电的全部特征信息非常困难,而且人工智能等方法通常需要大量的样本训练以确保放电模式识别的准确性,算法过程也较为复杂,对识别系统的运算、存储能力要求较高[7]。
本文采用互近似熵方法,对采集到的局部放电脉冲波形信息与经典的局部放电类型信息直接进行相似度匹配,只需运算得到反映两者波形相似度的互近似熵值,便可以识别出所采集的局部放電信号属于哪种局部放电类型,从而避免局部放电信号模式识别中不容易全面提取特征等难点。
1 局部放电特征分析
GIS设备的绝缘内部一旦存在缺陷,尤其当绝缘内气体击穿、小范围的固体或液体介质的局部击穿、金属表面的边缘或者尖角部位场强集中时,在电场强度的作用下,就可能不断地产生击穿和熄灭这类重复性的局部放电。
局部放电由于放电能量较小,虽然一般不会立刻损害GIS设备,但由于绝缘缺陷一直存在,运行过程中在工作电压的作用下会持续出现局部放电的情况,导致GIS设备绝缘性能不断下降,最终可能导致绝缘完全击穿,造成事故。因此,深入分析GIS设备局部放电的特征,及早发现和定位GIS设备放电类型,可以消除GIS设备局部放电带来的绝缘隐患。
局部放电过程存在电荷交换、电磁波辐射、能量损耗等复杂的电气现象,所采集到的局部放电信号和局部放电的类型、位置以及放电信号的传播路径等因素有关。由于放电位置多样化,局部放电信号传播路径具有不确定性和复杂化,不能简单地根据信号强度判断局部放电性质。但对于同一类型的局部放电,其放电脉冲波的分布和具体波形还是呈现比较明显的特征,具有较好的辨识度[8]。
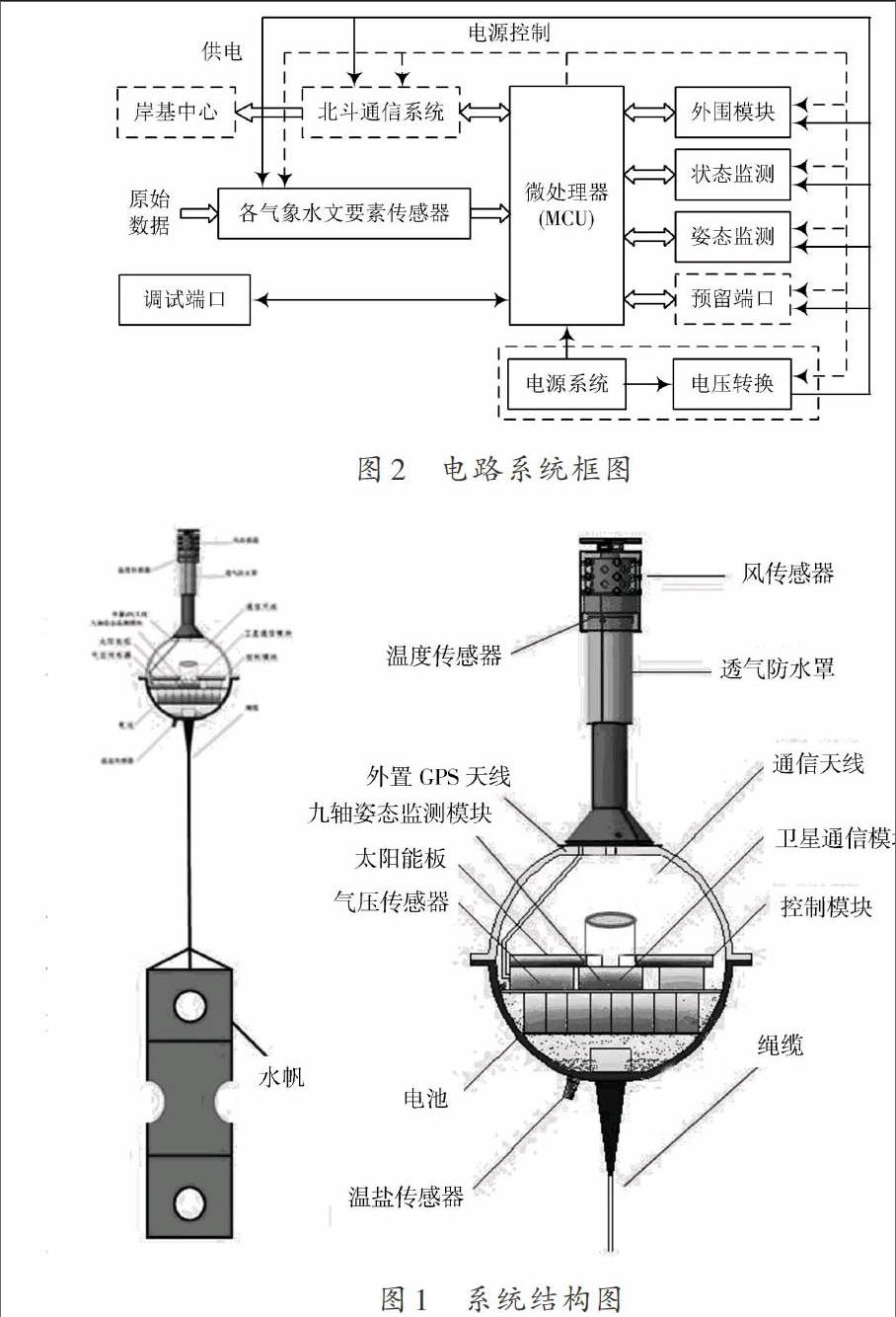
首先研究金属颗粒放电、悬浮电位体放电、绝缘件内部气隙放电、沿面放电、金属尖端放电等五种主要放电类型的脉冲波形分布情况,由于篇幅限制,取五种主要放电类型的一个工频周期内的脉冲分布情况进行重点分析,如图1所示。
金属颗粒性质的局部放电,放电持续时间较长,放电脉冲在时间轴上分布较广,在整个工频周期相位均有放电信号分布,但放电脉冲强度和脉冲间隔较为分化,极性效应不明显。
松动金属部件产生的悬浮电位体放电具有较好的规律性,放电脉冲强度较为一致,且相邻放电脉冲的间隔也比较接近。当悬浮金属体不对称时,正负半波检测信号有极性差异。
固体绝缘内部开裂、气隙等缺陷引起的绝缘件内部气隙放电,放电脉冲强度差异性比较大,脉冲分布也较为稀疏,脉冲之间的间隔也较分散。但放电相位较稳定,无明显极性效应。
绝缘表面金属颗粒或绝缘表面脏污导致的沿面放电,放电脉冲分散性比较大,脉冲强度具有较大的差异性,脉冲分布不均匀且相鄰脉冲间隔不统一,极性效应不明显。
处于不同电位的金属毛刺或尖端,由于电场集中导致的金属尖端放电,放电脉冲所呈现的特征较为明显,具体表现在放电脉冲分布较为集中,脉冲强度也非常接近,相邻脉冲的间隔也比较均匀。放电的极性效应比较明显,通常仅在工频相位的负半周出现。
不同类型的局部放电,其放电脉冲波在强度和时间间隔等方面呈现出不同的特征,具体表现在脉冲的分布波形具有差异性。为进一步分析不同类型的局部放电中单个放电脉冲的波形,以绝缘件内部气隙放电和悬浮电位体放电这两种类型的局部放电为例[9],如图2所示。
两种类型的单个放电脉冲都为持续时间极短的陡脉冲,具体表现为振荡衰减波形,放电脉冲的持续时间很短,波头的上升时间仅为纳秒级别。尽管两种不同局部放电类型的单个脉冲具有相似性,但具体的振荡衰减形式还是有所差别,悬浮电位体放电类型的单个脉冲振荡衰减程度相对而言更加激烈,幅值震荡幅度更大,衰减时间也更长。其他类型局部放电信号的单个脉冲波形也都有其自身特点。
结合局部放电所有脉冲的分布特点和单个放电脉冲的样式特点,构成了每种局部放电类型区别于其他类型的波形曲线。如果两条局部放电曲线波形很相似,则判断这两条曲线波形属于同一种局部放电类型的概率很大。因此,可以通过直接比较所采集的局部放电曲线波形和各种不同类型的经典局部放电曲线波形的相似度,来确定局部放电类型。由于直接采用反映曲线波形的采样数据进行运算比较,而不是从波形中提取某项特征以确定放电类型,因而可以避免因波形特征可能被遗漏而导致放电类型识别不准确的问题。
2 互近似熵及其应用
2.1 互近似熵
针对传统的熵存在需要大量采样数据、对噪声敏感和不易收敛等问题,Pincus从衡量时间序列复杂性的角度,于20世纪90年代提出了近似熵(Approximate Entropy,ApEn)和互近似熵(Cross Approximate Entropy,CApEn),以解决混沌现象中难以求解熵等难点[10]。
近似熵和互近似熵定义为:时间序列向量在由[m]维增加至[m+1]维时继续保持其相似性的条件概率。其物理意义是当维数变化时,时间序列向量产生新模式的概率大小,如果熵值越大,表明时间序列向量产生新模式的概率越大,也就是该序列向量越复杂。近似熵用于描述一个时间序列(比如,简单地理解为一条曲线波形)在模式上的复杂性(即相似性),是对自身波形复杂性的描述;而互近似熵则用一种条件概率来衡量两个时间序列(两条曲线波形)在模式上的相似性[11]。
互近似熵对两条时间序列向量的相似性进行定量表述,也就是描述两条曲线在时间轴上的相似模式,或者说描述两条曲线在模式上的相似程度有多大,若两条曲线波形越相似和接近,那么对应的互近似熵将越小。
互近似熵以统计的方法来表征两条曲线随着时间发展所呈现出来的差异或变化情况,以此来描述两条曲线波形的相似程度,互近似熵不用于重建整个曲线波形的全貌,因此只需要较短的数据样本就可以运算得到比较稳定的熵值。互近似熵所需数据窗较短的优点对于动态观察两条局部放电曲线相似度具有重要意义。可以采用一个较短的数据窗,在需要比较相似度的两条局部放电曲线中,从头到尾移动并计算每一条曲线位置上数据窗内的互近似熵值,从而通过互近似熵系列得到这两条波形曲线在时间轴上的相似度,互近似熵值越小,说明当前时刻的两条波形曲线越接近。
同时,互近似熵提出了相似容限的概念,互近似熵相当于相似容限条件下的统计概率。当参与互近似熵运算的曲线样本数据小于该相似容限时,小于相似容限的曲线细节信息就会被过滤掉,只保留幅值大于相似容限的相似模式。也就是说,幅值低于相似容限的噪声能够被抑制,互近似熵具有良好的抗干扰性能。虽然小波分析等抗干扰方法对于抑制白噪声等电磁干扰具有一定的效果,但现场应用中存在如何有效地区分局部放电信号和干扰信号频带等问题,尤其当干扰信号和局部放电信号具有非常相似的时频特性时,如何高效地抑制干扰信号并准确地提取局部放电信号仍然是局部放电类型识别的难点,互近似熵方法自身具有良好的抗低频干扰能力,因此本身作为一种抗干扰手段应用于局部放电的检测中。
互近似熵具有良好的适用性,对于信号类型没有严格限制,适用于各种信号的相似性分析。对于局部放电信号的多样化和不确定性,甚至可能包含各种随机的干扰,互近似熵方法也同样适用于局部放电信号分析。
2.2 互近似熵计算方法
对于包含[N]个采样数据[i(t)]的两条波形按以下步骤计算互近似熵值[12]:
(1) 对时间序列[i(t)]进行矢量重构,按顺序组成[m]维矢量,分别记为[Xk] 和[Xj:]
[Xk=i(k),…,i(k+m-1), k=1,2,…,N-m+1] (1)
[Xj=i(j),…,i(j+m-1), j=1,2,…,N-m+1] (2)
(2) 分别计算矢量[Xk]和[Xj]之间的距离,并记录下最大的矢量距离:
[dXk,Xj=max0≤p≤mi(k+p)-i(j+p)] (3)
(3) 给定相似容限[r,]统计[Xk]和[Xj]的矢量距离小于[r]的個数[Nm,r,]并计算[Nm,r]与总的矢量个数[(N-m+1)]的比值,即:
[Cm,r=(d(Xk,Xj) 式中:[Cm,r]反映序列中[m]维模式在相似容限[r]下相互近似的概率。具体应用中,通常取[m=2,][r=0.1~]0.25标准差。 (4) 先对[Cm,r]求取对数,进而求其平均值,从而获得两条曲线之间的互相关程度: [Om,rd(Xk,Xj)=1N-m+1k=1N-n+1lnCm,rd(Xk,Xj)] (5) (5) 当嵌入维度变为[m+1]时,重复上述步骤(1)~步骤(4)的运算过程,得到[m+1]维数时的互相关程度数值[Om+1,rd(Xk,Xj)]。 (6) 最后得到互近似熵值[CApEn(m,r)]: [CApEn(m,r)=Tm,rOU(i),U(j)-Tm+1,rOU(i),U(j)] (6) 3 基于互近似熵的放电类型识别 3.1 分析系统 安装在GIS设备的传感器采集局部放电信号后,送入到具有高频电流采集功能的前端智能电子设备中。局部放电信号首先经过由RC组成的简单式无源滤波回路或是性能更好的、以放大器为核心元件组成的有源滤波回路以硬件方式过滤掉明显的毛刺干扰。局部放电识别系统如图3所示。 经过滤波处理的局部放电信号接着进入信号调理回路,调理回路主要由阻抗匹配电路和放大电路组成。通过阻抗匹配电路减少局部放电信号传输过程中的损耗,同时利用放大电路将较为微弱的信号调整成符合模数转换器电平接口的信号;模数转换器进而将采集的局部放电信号由模拟量形式转换成数字量形式,并通过对应的通信口(CAN、Profibus各种现场总线、光纤以太网等通信方式)将局部放电数据发送到后台的局部放电分析系统。 局部放电分析系统由性能强大的工控机甚至服务器组成,实现局部放电信息的存储、放电类型识别等处理功能,并最终以告警等方式显示局部放电的分析结果通知运行人员。 局部放电分析系统接收来自通信网络的局部放电数据,并将其存储到采样值数据库,该数据库专门用于存储现场采集的局部放电数据。同时,局部放电分析系统配备经典值数据库,该数据库已事先存储由出厂试验数据或历史试验数据等组成的局部放电经典值数据和对应的局部放电类型。数据库可以采用以局部放电类型为关键字的树形结构,这样在局部放电类型识别算法应用时能迅速地查找到对应的局部放电经典值数据,并调出到局部放电类型识别算法中,作为算法识别时进行数据比较的依据。 局部放电类型识别算法是识别分析系统的核心,本文采用互近似熵方法直接对待识别的局部放电波形和五种经典的局部放电波形分别进行两条曲线的相似度比较。局部放电类型识别算法从采样值数据库和经典值数据库调出相应的两条曲线波形数据,并根据互近似熵方法算出的熵值确定局部放电类型,最后将识别的局部放电类型通过局部放电分析系统的显示界面提醒现场运行人员。 3.2 算法流程 具体的局部放电类型识别算法实现上,采用互近似熵算法对采样值数据和各种经典局部放电类型的典型数据进行熵值运算,并通过运算得到的熵值进行波形相似度识别。熵值最小对应的典型放电类型与该采样值数据(也就是待识别的局部放电)的波形相似度最高,实现流程如图4所示。 具体的算法步骤主要包括: (1) 从采样值数据库调出待识别的局部放电波形数据,将局部放电采样数据按顺序形成数组[{is},]得到二维的局部放电类型待识别矢量。 (2) 从经典值数据库调出五种经典局部放电类型的波形数据,将五种经典的局部放电类型的数据按顺序分布形成数组[ic,k(k=1,2,…,5)],得到五组局部放电的经典类型矢量。 (3) 充分利用互近似熵算法自身具有的抗噪声功能,类型待识别矢量[{is}]不再采用小波去噪等滤波方法,分别将直接和经典类型矢量[ic,k(k=1,2,…,5)]进行互近似熵运算,得到五种经典局部放电类型对应的五个熵值CApEn。 (4) 选取其中最小的熵值CApEn,理论上表明最小熵值对应的经典放电波形和待识别的局部放电波形相似度最高,即这两者局部放电类型最接近,即可初步判定待识别的局部放电类型为该熵值对应的经典放电类型。 (5) 进一步分析该最小熵值CApEn是否在合理区间。如果最小熵值CApEn明显过大,说明待识别的局部放电类型不在这五种经典的放电模式中。如果最小熵值在合理的区间内,说明该熵值对应的经典放电类型是待识别的局部放电类型。 4 实 验 为了验证互近似熵方法在局部放电类型识别中的效果,在GIS设备上进行模拟金属颗粒放电、悬浮电位体放电、绝缘件内部气隙放电、沿面放电、金属尖端放电五种类型的局部放电实验,局部放电实验过程中利用采样速率高达800 MS/s的采集器捕捉局部放电脉冲信号,并连续采集50个工频放电周期的局部放电样本数据,对得到的样本数据与经典的局部放电类型数据进行互近似熵值计算,运算结果如表1所示。
根据表1的互近似熵值,可以分析得到基于互近似熵的局部放电方法具有以下特点:
(1) 当待识别样本的局部放电类型与典型的局部放电类型相匹配时,通过互近似熵运算得到的熵值比较小,在0.2~0.4之间,说明两者的波形相似度高,在模式上接近;当待识别样本的局部放电类型与典型的局部放电类型不一致时,对应的互近似熵值大于0.6,明显区分于两者类型一致时的互近似熵值。说明基于互近似熵方法的局部放电类型识别具有较好的区分度。
(2) 对随机生成的样本数据与典型的局部放电类型数据进行互近似熵运算,得到的所有熵值都大于0.8,说明随机生成的样本数据波形与典型的局部放电类型波形在模式上差别很大,可以很容易地排除隨机生成的样本数据不属于文中所述的五种局部放电类型。
(3) 进一步观察待识别样本的局部放电类型与典型的局部放电类型相匹配时熵值的大小情况,金属尖端放电和悬浮电位体放电两者类型的互近似熵值最小,说明待识别样本波形和对应的典型波形的相似度更高,与这两种放电类型的波形具有较好的规律性有关。金属颗粒放电、绝缘件内部气隙放电和沿面放电三种放电类型的互近似熵值逐步增大,说明这三种类型的局部放电波形趋向于浑浊状态,波形的信息较为分散和杂乱,不规则性逐步明显。
(4) 本文方法没有采用滤波算法,就直接对可能包含各种噪声的局部放电采样数据直接进行互近似熵运算,上述的实验结果分析表明,互近似熵值能准确区分局部放电的类型,表明互近似熵算法具有较好的噪声容忍度,局部放电应用中可以减少传统局部放电类型识别所需的算法去噪这一环节,具有较高的算法效率。
5 结 语
本文以典型的局部放电波形为基准,对采集到的局部放电脉冲波形信息与经典的局部放电类型信息直接进行相似度匹配。采用具有算法实现简便、同时具有抗噪能力、所需数据窗短等优点的互近似熵方法,通过直接运算得到反映两者波形相似度的互近似熵值,便可以识别出采集的局部放电信号的类型。避免了局部放电信号模式识别中不容易全面提取局部放电特征,及神经网络等局部放电识别方法所需的培训样本大、不易收敛、计算过程复杂等难点。
参考文献
[1] 徐长宝,庄晨,蒋宏图.智能变电站二次设备状态监测技术研究[J].电力系统保护与控制,2015,43(7):127?131.
[2] 周沙,景亮.基于矩特征与概率神经网络的局部放电模式识别[J].电力系统保护与控制,2016,44(3):98?102.
[3] 苑津莎,尚海昆,王瑜,等.基于相关系数矩阵和概率神经网络的局部放电模式识别[J].电力系统保护与控制,2013,41(13):110?115.
[4] 臧怀刚,李清志.改进的EMD方法在局部放电信号提取中的应用[J].电力系统及其自动化学报,2014,26(11):78?81.
[5] 邓雨荣,郭丽娟,郭飞飞,等.引入二代小波的自适应BP神经网络局部放电故障识别[J].电力建设,2013,34(6):87?91.
[6] 杨志超,范立新,杨成顺,等.基于GK模糊聚类和LS?SVM的GIS局部放电类型识别[J].电力系统保护与控制,2014,42(20):38?45.
[7] 王立欣,诸定秋,蔡维铮.局部放电在线监测中基于小波变换的阈值消噪算法研究[J].电网技术,2003,27(4):46?48.
[8] 严璋,朱德恒.高电压绝缘技术[M].北京:中国电力出版社,2007.
[9] 任重.典型SF6气体绝缘缺陷局部放电脉冲的Gabor特征识别[J].高压电器,2015,51(12):142?148.
[10] 郝晓弘,田江博,陈伟,等.基于信息熵和数学形态学的电压跌落持续时间检测方法[J].电力系统保护与控制,2012,40(11):30?35.
[11] 符玲,何正友,麦瑞坤,等.近似熵算法在电力系统故障信号分析中的应用[J].中国电机工程学报,2008,28(28):68?73.
[12] 何文平,何涛,成海英,等.基于近似熵的突变检测新方法[J].物理学报,2011,60(4):813?821.
