适用于液氨类介质的垂直型齿轮泵设计

李玉龙， 文昌明， 钟 飞

(成都大学 机械工程学院， 四川 成都 610106)

适用于液氨类介质的垂直型齿轮泵设计

李玉龙， 文昌明， 钟 飞

(成都大学 机械工程学院， 四川 成都 610106)

为改善与提高液氨类介质齿轮泵的进口空化性能和有效容积率，从进口流道的方向与位置设计及齿轮副基本参数优化等方面，提出一款来流方向垂直于泵内搬运方向即具有垂直型流向的齿轮泵.基于现有的优化模型，通过单位排量体积优化目标的公式修正，新增有效容积率约束，新建根切重合度约束，优化出齿轮副的模数、齿数、变位系数、齿顶高系数等基本参数，并据此进行相关分析.结果表明：现行通过主动轮齿顶啮合计算出的重合度不可靠，只有通过从动轮齿根点能否进入啮合计算出的重合度，才能保证齿轮副的连续传动；垂直型流向有利于进口空化性能的提高和困油性能的改善，外形上具有轴向尺寸小、径向尺寸大的几何特征等.方法为适用于任何介质的齿轮泵设计提供了一种新的思路.

齿轮泵；液氨；进口空化；重合度；进口流向；有限容积率；优化设计

0 引 言

在空间狭窄与微重力等环境下，外啮合齿轮泵因具有结构简单、体小量轻、高可靠性、长寿命及良好的自吸性等特点，被认为是替代现有离心泵的较好选择[1].目前，外啮合齿轮泵开始应用于大型航天器的热控系统中[2-3]，由于此类系统常用介质为具有相似物性的液氨、乙二醇、二氧化碳、氟里昂等液氨类介质[2-3]，其超低黏度物性和易空化特性等对泵的性能、设计与加工提出了较高的要求[4].当常规油介质类齿轮泵采用此类超低黏度介质时，进口流域的空化现象会比较严重，内泄漏也会大幅增加，从而引起泵容积率的快速下降和出口压力上不去等情况出现.因此，该类泵的设计，必须着重解决在给定条件下较好的空化性能、较高的容积率和体积最小化等技术难题.

1 进口流道的流向设计

一般来讲，影响泵的进口流域空化的因素，主要涉及边界条件，如压强、流速、黏度、表面张力、含气量及来流条件等多方面.

针对现有齿轮泵而言，常规上虽然可以通过提高进口液氨类介质的过冷度来改善进口流域的空化性能.但从新产品设计的角度看，还可以通过对来流条件(如来流方向、流道)等局部结构创新和影响空化(如困油)现象的齿顶线速度最小化二个方面来降低轻产品后续过冷度的实现成本.

目前，针对提高空化性能的流道形状改善，文献[5]给出了一些有效的建议.至于流道方向的改善，尚无相关的文献报道.为此，本研究设计提出一款具有垂直型流向的齿轮泵，具体如图1所示.

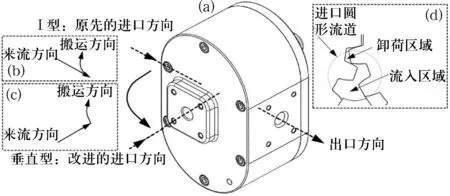
图1垂直型流向齿轮泵

该齿轮泵的特点在于将常见进、出口方向相一致的I型流向改为进、出口方向相垂直的垂直型流向(见图1(a)).

在I型流向中，介质的来流方向和泵内搬运方向成钝角(见图1(b))，相互方向上具有一定的抵触影响，加上流体旋转搬运中的离心力作用，使得来流很难进入到齿轮的根部区域，导致空化现象发生.

而在垂直型流向中，由于进、出口方向相垂直(见图1(c))，方向上没有抵触影响，且来流直接从齿轮根部进入(见图1(d))，空化现象不易发生.另外，进口流道的圆形轮廓采用圆形卸荷槽设计[6]，兼具有困油卸荷的功效(见图1(d)).

2 进口流道的形位设计

泵的进口流道的形位尺寸设计及确定(见图2)主要涉及图2中圆形流道的直径DU及从圆心到主从动齿轮中心线的距离HU.文献[6]给出了DU和HU的相关计算方法.在此基础上，本研究采用图解法来获取.

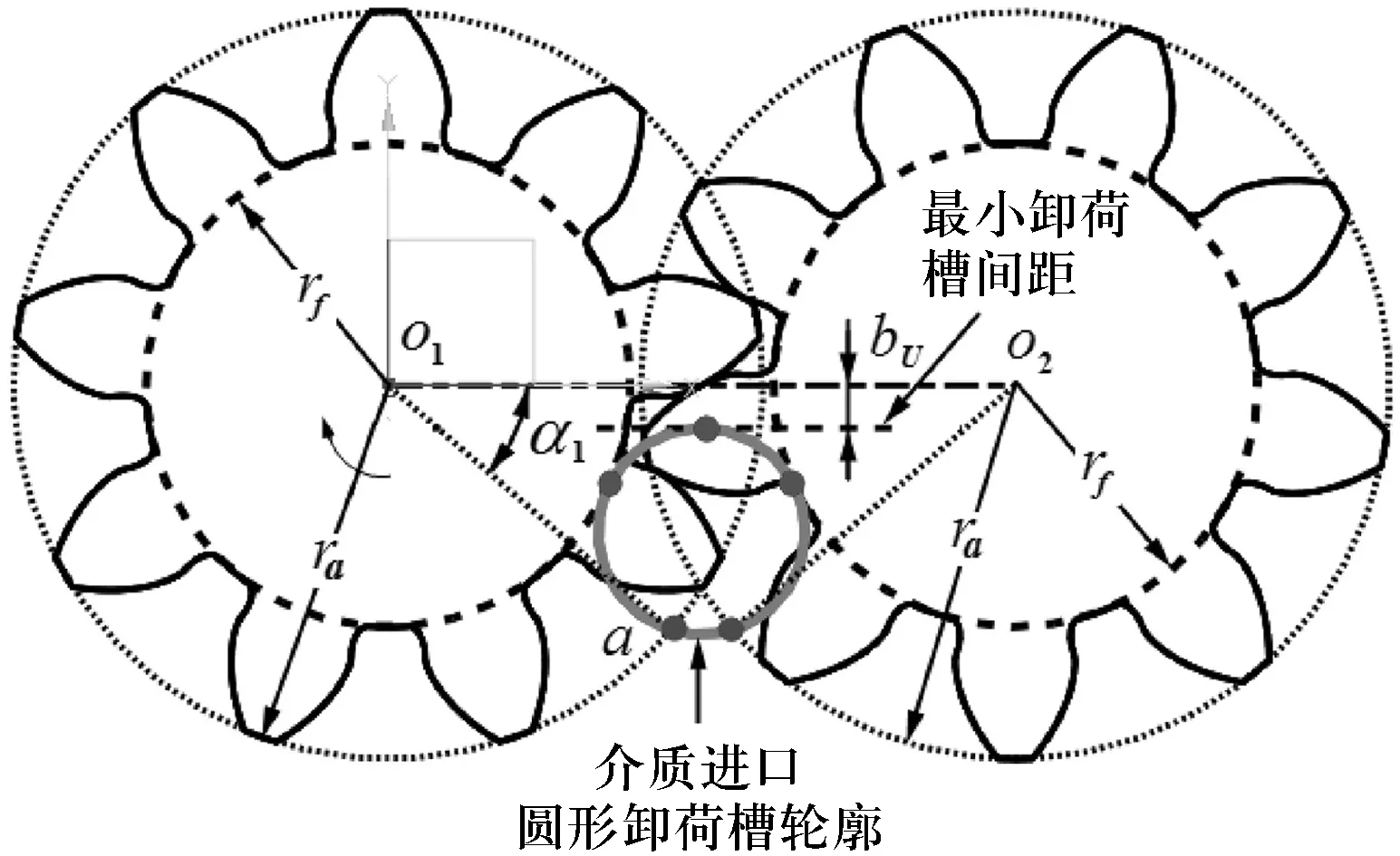
图2进口流道形位尺寸的确定

图2中，针对无侧隙或侧隙很小的情况，文献[7]给出了如式(1)所示的最小卸荷槽间距bU的计算公式，

bU=0.25pbcosα′

(1)

同时，进口流道的圆形轮廓分别与最小卸荷间距线、主从动齿轮的2个根圆分别相切，从而可以惟一确定出DU和HU的值，再由该圆形轮廓与主从动齿轮顶圆的2个交点确定进口夹角α1.

3 基本参数的优化设计

作为齿轮泵核心的齿轮副基本参数，既是泵整体设计的开始，也是后续其他零件设计的依据，取值是否合理，直接影响到泵的性能、噪声和寿命等.目前，国内外针对齿轮泵的这对啮合齿轮展开了大量的优化设计，优化流程主要是基于泵给定的额定压力、额定转速和额定流量等原始设计参数，通过对泵的流量脉动率、单位排量体积及径向力等目标的函数值最小化，探求出泵用模数、齿数、齿顶高系数、变位系数、甚至于压力角等5个基本设计参数.不过，由于绝大部分针对的是油类介质，内泄漏或有限容积率因素不纳入考虑范围.

影响齿轮泵容积率的因素，主要包括径向泄漏Qa，轴向泄漏Qz，齿面接触摩擦副对应的啮合泄漏，以及介质压缩时的弹性损失，其中，Qa和Qz约占总损失的90%，故泵的总泄漏量Qlose可采用(1.1(Qa+Qz))来近似[7].如果泵的额定流量记为Qe，则泵的有限容积率λV为，

λV=1-Qlose/Qe=1-(1.1(Qa+Qz))/Qc

(2)

文献[7-8]分别给出了Qa和Qz的计算公式.其中，文献[7]计算值略大，由此计算出的容积率偏安全，故本研究采用文献[7]的计算公式.

绝大多数优化模型中，其重合度的计算采用主动齿轮齿顶点啮合时如式(2)所示的传统计算公式[9]，简称为齿顶重合度εa.

εa=z(tanαa-tanα′)/π

(3)

式中，z、αa、α′为泵上参数完全相同的2个齿轮的齿数、顶圆压力角与节圆压力角.

同时，齿轮泵为减小体积和增大排量，常采用根切齿轮，这往往会造成主动齿轮的齿顶点进入不了啮合.此时，可按照从动齿轮的根切点的啮合情况来计算相应的重合度，简称为根切重合度εw，其计算式[9-10]为，

f0=rf+r0(1-sinα)

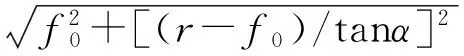
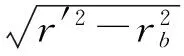
→αw=acos(rb/rw,1)

→εw=z(tanαw-tanα′)/π

(4)

式中，f、rw,2、rw,1与αw分别为从动轮上根切点到节点的距离、根切圆半径、主动齿轮对应于从动轮上根切点啮合时的啮合半径与压力角；r0为加工齿轮的齿条刀具的齿顶圆角半径；ra/r'/r/rb/rf和α为泵上参数完全相同的2个齿轮的顶圆/节圆/分度圆/基圆/根圆的半径和分度圆压力角.

大部分优化模型中有关泵体积的计算多以齿轮副所占空间来简化.例如，文献[9]所给出的优化模型中，采用如式(5)所示的单位排量体积Vq最小作为优化目标，其特点在于单位排量q的计算中引入了λV.泵的体积V以齿轮副—轴所占空间体积实现精确计算，以模数m、齿数z、齿顶高系数h*及变位系数x作为设计变量.在约束函数中，添加λV≥λV,e的约束，并采用如式(3)所示的根切重合度.

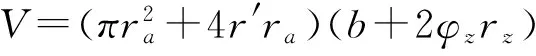
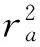
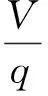
(5)式中，ne为额定转速，r/min；φz为轴颈长径比(轴颈长/轴直径)；rz为轴半径，mm；b为齿宽，mm；pb为齿轮基节，mm；Kc为外啮合齿轮泵类型系数，当采用无侧隙(或侧隙很小)和仅进口侧有卸荷槽时[7]，有，

(6)

传统上，齿轮副所占空间的单位排量体积Vqc为，

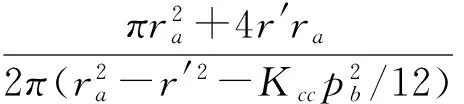
(7)

式中，Vqc显然与齿宽b没有关系，且，

(8)

4 实例计算及分析

泵的整体设计要求为：额定压力0.5 MPa，进口压力0.1 MPa，Qe=8 L/min，ne=1 500 r/min，介质黏度0.0006 Pa·s，λV,e=90%.

泵的结构设计要求为：rz=5 mm，实际径向间隙0.03 mm，实际端面轴向间隙0.02 mm，过渡区起始角40 °，过渡区终止角300 °，齿顶转速极限15 m/s，φz=1，齿轮最小幅宽值1.5 mm.

计算时，以顶隙系数0.15，α=20°，r0=0.5 mm，以及式(9)所列的几何约束，作为齿形设计的要求.由于该类泵的进、出口压差一般只有几个大气压，因此，对齿轮—轴的强度、刚度等约束不作要求，故约束为，

0.5≤m≤6;8≤z≤20；0.8≤h*≤1.25；

16°≤α′≤35°；0.2≤φc≤1.5；

1.05≤εw≤1.3；-0.5≤x≤1

(9)

1)考虑λV≥λV,e的容积率约束，重合度约束采用式(4)中ε=εw后的优化结果，如表1中分类1所示，对应的齿轮副传动如图3(a)所示，虽有根切，却很轻微，能保证齿轮副的正常传动.此时，λV≥λV,e=90%，符合设计要求，单位排量体积为3.766，εw=1.05≠εa=1.25，bU=1.66 mm，由图解法得DU=Φ8.5 mm，HU=bU+0.5DU=5.91 mm，α1=39.7 °.齿顶转速Vra=2.455 m/s远小于极限值15 m/s，此明显有利于提高进口流域的空化性能.

表1中的分类1为适用于超低黏度介质齿轮泵的优化设计结果.泵具有轴向尺寸短、径向尺寸大的外形特征，该特征相当于加长了径向、轴向的泄漏路径，有利于降低内泄漏和提高容积效率.

2)考虑λV≥λV,e容积率约束，重合度约束采用ε=εa后的优化结果如表1分类2所示.对应的齿轮副传动如图3(b)所示，由于εw=-0.025，根切非常严重，齿轮副不能正常传动.

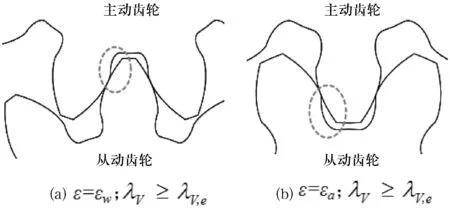
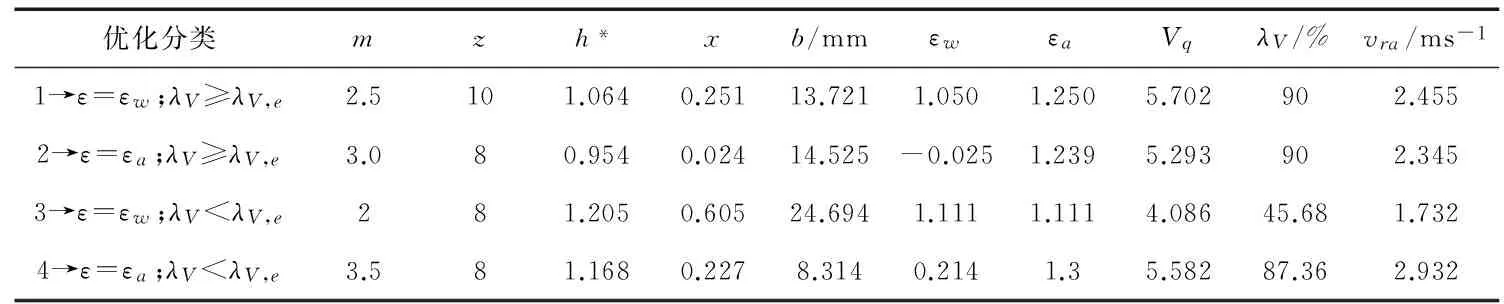
图3 2种齿轮副的传动示意

3)不考虑容积率约束即λV<λV,e，重合度约束采用ε=εw后的优化结果如表1分类3所示.此时，λV=45.68%<λV,e=90%，远不能达到设计要求.

4)不考虑容积率约束即λV<λV,e，重合度约束采用ε=εa与式(7)作为目标后的优化结果如表1分类4所示.此时，εw=0.214，根切严重，齿轮副不能正常传动.

5 结 论

本研究设计的垂直型流向的齿轮泵既利于提高进口流域的空化性能，也利于改善进口侧的困油现象.超低黏度介质齿轮泵具有轴向尺寸短、径向尺寸大的外形特征，有利于降低内泄漏和提高容积效率.本研究认为，齿顶重合度代替根切重合度的计算方法不可靠，计算结果无法实现齿轮副连续传动的要求.

[1]Schuller M,Kurwitz C,Goldman J,et al.CustomunitpumpdesignandtestingfortheEVAPLSS[C]//40thInternationalConferenceonEnvironmentalSystems.Barcelona，Spain:NASA Johnson Space Center,2010：11-15.

[2]Es J V,Donk G V,Pauw A，et al.AMS02Trackerthermalcontrolsystem:looplayout&specificationofloopcomponents[R].Warrendale,PA,USA:SAE International,2004.

[3]Bazzo E，Riehl R R.Operationcharacteristicsof1small-scalecapillarypumpedloop[J].Appl Therm Eng,2003,23(6)：687-705.

[4]黄臻成．航天热控用机械驱动CO2两相系统的数值模拟及控温特性分析[D]．广州：中山大学，2009．

[5]何渊博，梁银川，张小卫.齿轮泵进口流道设计对汽蚀性能的影响[J]．燃气涡轮试验与研究，2014，27(4)：29-41．

[6]李玉龙．齿轮泵圆形卸荷槽下的困油压力分析[J].中国农业大学学报，2014，19(4)：32-36.

[7]何存兴．液压元件[M]．北京：机械工业出版社，1982．

[8]王强．水压外啮合齿轮泵关键技术的研究[D]．哈尔滨：哈尔滨工业大学，2008．

[9]李玉龙,孙付春,姚旗，等.航天器用超低黏度齿轮泵轻量化设计[J].农业工程学报,2016,32(21):109-114.

[10]李玉龙,袁影,吴柏强，等.泵用齿轮副根切重合度的公式创建[J].机床与液压,2017,45(1):84-88.

Abstract:To improve the effective volume rate and input cavitations performance of external gear pump of liquid ammonia medium,and from the perspectives of innovative design of input flow direction and flow channel location as well as the basic parameters optimization design of gear pairs,an gear pump with vertical-shaped flow direction,which meant the input flow direction was perpendicular to the moving direction was put forward.Based on the existing optimization model,and the correction of optimization formula of unit displacement volume,the new constraint functions of effective volume rate were added,the new constraint function of coincidence degree factor appropriated for gear undercut was established, and the basic parameters such as modulus and tooth number and displacement coefficient and addendum coefficient of gear pairs were optimized.Then,the correlation analysis was carried out.All results showed that the current coincidence degree calculated from addendum peak contact status of driving gear was not reliable; the continuous gear transmission was guaranteed only by the coincidence degree calculated according to whether the undercut point of driving gear could come into mesh;the input cavitations performance and trapped-oil performance improved because of the vertical-shaped flow direction;and the appearance features of a smaller axial size with a larger radial size was endowed in the vertical-shaped gear pump.Finally,a new design method was provided for gear pump applicable to any medium.

Keywords:gear pump;liquid ammonia;input cavitations;coincidence degree factor;input flow direction;effective volume rate;optimization design

GearPumpDesignwithVertical-shapedFlowDirectionAppropriateforLiquidAmmoniaMedium

LIYulong,WENChangming,ZHONGFei

(School of Mechanical Engineering, Chengdu University, Chengdu 610106, China)

TH325；TH137.3

A

1004-5422(2017)03-0285-04

2017-06-14.

四川省教育厅自然科学基金(16ZA0382)资助项目.

李玉龙(1968 — )， 男， 博士， 教授， 从事齿轮泵理论与现代设计方法研究.