基于Hu不变矩的图像形状特征提取研究
2017-10-12刁彦华孟子钰王晓君
◆刁彦华 孟子钰 王晓君
(河北科技大学(石家庄)信息科学与工程学院 河北 050018)
基于Hu不变矩的图像形状特征提取研究
◆刁彦华 孟子钰 王晓君
(河北科技大学(石家庄)信息科学与工程学院 河北 050018)
本文提出一种基于形状的图像特征提取方法。首先用Canny算子和形态学算子分别对图像进行轮廓提取。通过对相同形状图像进行放大、缩小、旋转等变换计算归一化中心矩、Hu不变矩、离心率,并对不同形状的图像进行上述操作,结果表明不变矩、离心率能较好地对图像形状进行描述,具有很高的应用价值。
轮廓提取;形状特征;Canny算子;形态学算子;Hu不变矩;离心率
0 引言
形状是刻画物体的基本特征之一,用形状特征区别物体非常直观[1]。形状特征提取的准确率对图像检索的结果有直接的联系,因此研究图像的形状特征提取有重要意义。文中用传统的Canny算子和形态学算子把目标的轮廓提取出来,取得了很好的实验结果。形状特征可以用不变矩和离心率来描述,实验结果表明:不变矩和离心率能较好地对形状进行表达。
1 轮廓提取
在图像处理领域轮廓提取占据着一个重要角色。应用于目标识别、目标分类、图像分割等,是图像分析技术的基础。轮廓检测是形状识别的一个重要基础,从图像中提取目标的完整轮廓,能够为图像后续研究提供很大的帮助。边缘是指图像中像素灰度有阶跃变化或者是屋顶变化的像素集合。图像中目标的边缘是由灰度不连续利用边缘灰度变化的一阶或二阶导数特征能将边缘点检测出来。边缘检测算子包括Laplacian算子、Log算子、Canny算子、Sobel算子、Prewitt算子等。本文主要讲Canny算子和数学形态学算子。
1.1 Canny算子
Canny算子于1986年由John Canny提出[2],广泛应用于图像处理领域。Canny 算子边缘检测的方法是寻找图像梯度的局部最大值。梯度是用高斯滤波器的导数计算的 Canny 方法使用两个阈值来分别检测强边缘和弱边缘。Canny 算法基于梯度幅值的双阈值方法往往难以在抑制噪声的同时保护低强度边缘,在一定程度上影响了其边缘检测的效果,并且高低阈值需要自己设定,自适应能力较差[3-4]。在实际应用中Canny算子对有噪声的图像提取边缘能力较低,但是为了更好的抑制噪声,需要增大方差来控制图像的平滑程度,与此同时这会导致模板变大,使边缘产生偏移。Canny 算子边缘检测的具体算法步骤如下[5]:
(1)去掉图中的噪声及使用高斯滤波器对图像进行滤波;
(2)对处理后的图像(滤波后)中的每一个像素,计算其梯度幅值A和方向 ;
(3)对梯度幅值进行非极大值抑制;
(4)用双阈值算法检测和连接边缘。
Canny 算子实际上是高斯函数的一阶导数,是图像的高斯函数平滑和梯度运算相结合的算子,虽然不具有旋转对称性,但在边缘方向对称且沿梯度方向具有反对称性,这样使得该算子可在抗噪与边缘精确定位之间取得很好的折中效果。 但是,由于Canny 边缘检测算子用高斯滤波平滑图像,边缘作为高频部分被平滑,使得一些边缘成为伪边缘。
1.2 形态学算子
数学形态学算子用于边缘检测的基本理论是运用结构元素对原图进行腐蚀操作,然后再用原图与腐蚀之后的图像相减。形态学算子与传统的微分算法提取边缘相比的优点是对于噪声不敏感。它在运用合适的结构元素加上进行运算后(如开、闭运算)均能滤除图像中的噪声,保持原图的基本信息,图像几何特征突出,为后续图像进行一系列处理埋下了基石。
2 形状特征提取方法
形状特征提取主要分为两大部分:基于区域内部的形状提取方法和基于区域外部的形状提取方法。如骨架、矩形度、圆形度、Fourier描述子、角点检测、Hu不变矩等。文中主要研究的方法是基于区域内部变换分析法的Hu不变矩。
2.1 Hu不变矩
Hu不变矩是1962年提出的,具有对图像的平移、旋转、尺寸大小的变化而变化。对于离散的数字图像阶矩定义为[6]:

对于离散数字图像 f( x, y)的中心距定义为:

2.2 物理意义
零阶矩m00表示二值图像的面积;对灰度图像而言是图像灰度 f( x, y)的总和。一阶矩:图像的中心或者是灰度图像的重心表示为则
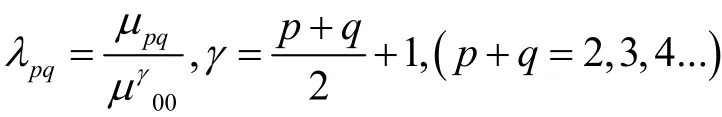
利用二阶、三阶的归一化中心距可以7个不变矩组:
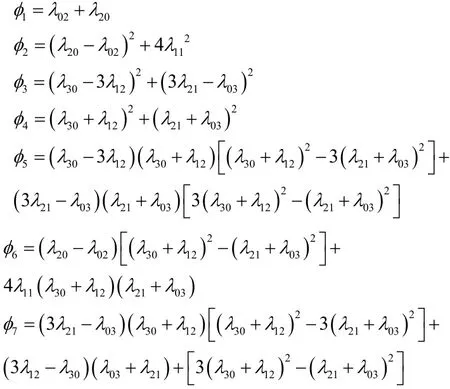
2.3 离心率
为了更好地提取形状特征,提高图像的检索效率、准确率,将离心率e和Hu不变矩的结合。离心率e代表了图像长轴与短轴之间的比值,满足几何变换不变性。将两者有效的结合在一起,就得到了图像的全局形状特征向量[8]。离心率的计算公式如下所示:

3 试验方法及结果分析
3.1 轮廓提取实验结果及分析
Canny算子在传统的边缘检测算子中算是一个较好的方法,相对于Sobel算子、Roberts算子能够提取出图像边缘信息。由图1可以看出,Canny算子虽然能够提取图像的边缘,但是提取的边缘线非常细,不连续平滑且提取出来的细节部分较多有好多的伪边缘。这主要是因为传统的边缘检测算子在提取边缘时抑制噪声的能力较弱造成的。

图1 Canny算子边缘检测图
而基于数学形态学算法提取的图像边缘信息时具有很高的抗噪声能力,在进行开、闭运算的同时,就可以滤除图像的噪声。所以提取的边缘比较平滑、连续和准确,与Canny算子相比少了较多的伪边缘。与Canny算子相比形态学算子在对图像边缘检测上还是具有很大优势的。图2为形态学算子边缘检测图。

图2 形态学算子边缘检测图
3.2 不变矩计算及分析
用于计算不变矩以及离心率的彩色RGB图像如图3所示。首先将彩色图像灰度化,然后用Canny边缘检测提取边缘保留边缘灰度图像,直接变为二值图像。在此基础上计算每副图像的不变矩的值。计算的不变矩和离心率的值如表1所示。由表1可知不变矩和离心率能较好的描述形状信息(注:表中的和e的值是不变矩的结果是取以十为底的对数后取模的值)。

图3 计算不变矩样图
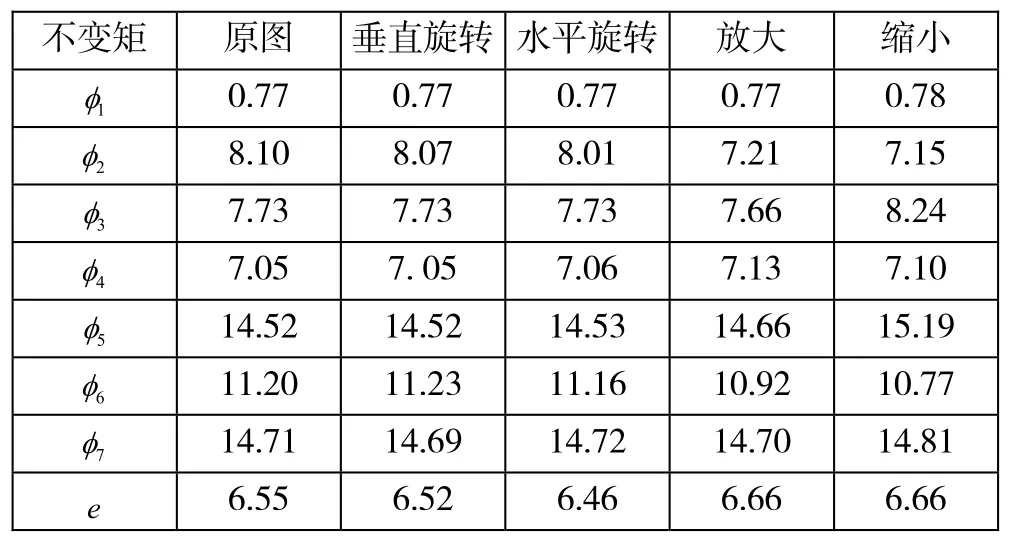
表1 不变矩和离心率的计算结果
4 结束语
文章首先采用了Canny算子和形态学算子进行轮廓提取,并分别简单介绍了这两种算子边缘检测的原理。分析和比较了Canny算子和形态学算子在进行边缘提取时的优缺点。指出了Canny算子提取时产生伪边缘的原因,主要是抑制噪声的能力不够好造成的;同时也指出了形态学算子在提取边缘时通过开闭运算能有效地去除噪声,并且提取的边缘比较平滑、连续。形状特征提取采用了 Hu不变矩和离心率相结合,实验数据表明,Hu不变矩具有旋转、尺度不变性,能够较好地对形状信息进行描述。
[1]王吉林,赵力.数字图像形状特征提取的研究[J].微电子学与计算机,2010.
[2]刘刚,王立香,董延.MATLAB数字图像处理[M].北京:机械工业出版社,2010.
[3]姜普泽田,张兴国.数学形态学与 Canny 算法结合的禽蛋检测边缘提取[J].机电技术,2013.
[4]王会江.结合Canny算法和Hough变换的轴类零件边缘提取[J].机电工程技术,2016.
[5]林卉,赵长胜,舒宁.基于 Canny 算子的边缘检测及评价[J].深圳大学学报(理工版),2005.
[6]黄勇,王崇骏,王亮等.基于形状不变矩的图像检索算法的研究[J].计算机应用研究,2004.
[7]H.J.Zhang, D.Zhong. A Scheme for visual feature-based image indexing[C].Proc.of SPIE conf.on Storage and Retrieval for Image and Video Databases III,SanJose,1995.
[8]雷晨光.基于区域不变矩的形状匹配技术的研究及应用[D].大连理工大学,2014.
