TWINE密码算法的多维零相关线性分析

◆程 璐

(武警工程大学 陕西 710086)

TWINE密码算法的多维零相关线性分析

◆程 璐

(武警工程大学 陕西 710086)

TWINE密码算法的分组长度为64bit，支持2种密钥长度，分别为TWINE-80和TWINE-128，本文的研究对象为TWINE-128。本文构造了一个与TWINE算法等价的传统的双分支Feistel结构。利用此结构特性，首先构造了算法的14轮零相关线性逼近，之后对24轮的TWINE-128进行了多维零相关线性分析。攻击过程的数据复杂度约为262.1个明密文对，计算复杂度为2107.1次24轮加密。由此可得，缩减轮数（24轮）的TWINE-128对于零相关线性分析方法是不安全的。

分组密码；TWINE密码算法；线性掩码；线性逼近；零相关线性分析

0 引言

TWINE算法是在 2012年的 SAC上由 Suzaki[1]等人提出。TWINE算法采用16分支的广义Feistel结构，共有16轮迭代。其明文分组长度为64bit，密钥长度有两种80bit和128bit，分别可记作 TWINE-80和 TWINE-128。本文的研究对象为TWINE-128。零相关线性分析方法由Bogdanov等[2]在2012年第一次提出， Bogdanov等[3]于FSE2012提出利用多条零相关线性逼近区分统计分布的理论模型，即多重零相关线性分析。Bogdanov等[4]于ASIACRYPT2012提出多维零相关线性分析的模型。

1 TWINE算法简介

TWINE算法采用16分支的广义Feistel结构，迭代轮数为36，其轮函数F包括3种操作：轮密钥加、4bit的S盒变换及置换P，具体过程如图1所示，其中，每个方框代表半字节单元。TWINE算法最后一轮无置换P。

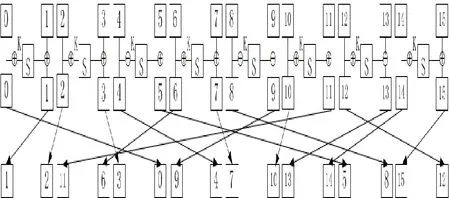
图1 TWINE算法的轮函数

S盒定义如表1所示，轮置换p(h)定义如表2所示。

表1 TWINE的S盒

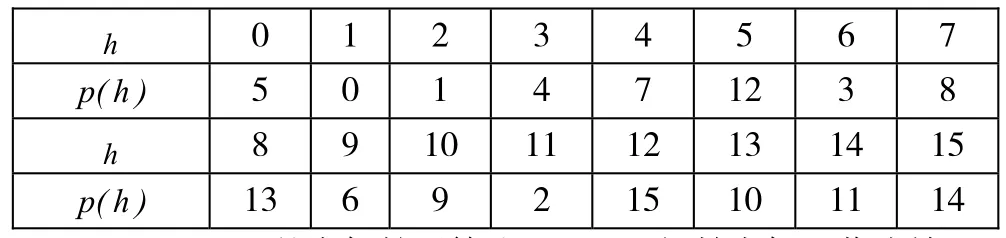
表2 TWINE置换层P

TWINE-128的密钥扩展算法以128bit初始密钥K作为输入，每轮输出32bit轮密钥。为便于分析，将TWINE算法的16分支结构等价为传统的双分支Feistel结构，其等价结构如图2所示。

该等价结构将TWINE算法的扩散层分为两个部分，分别对两个分支的数据进行置换。P1,P2如表3所示。

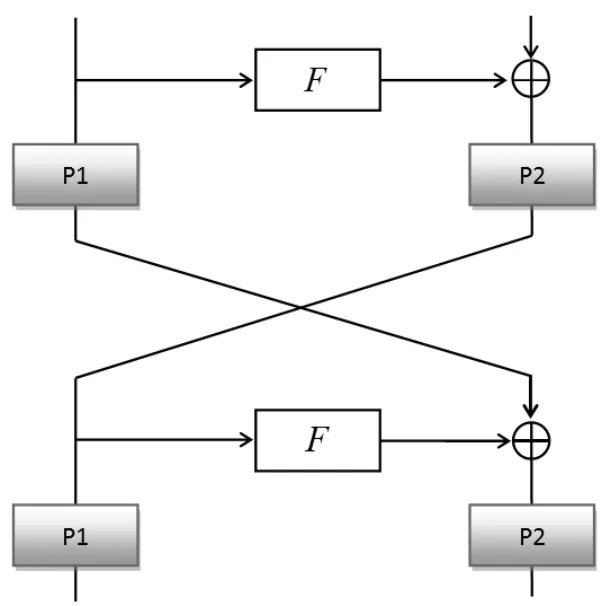
图2 TWINE算法等价结构

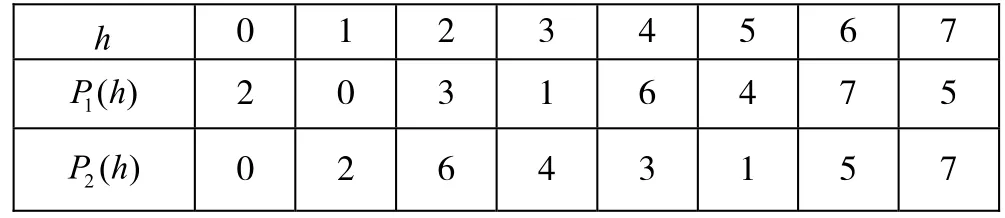
表3 P1P2置换表

2 TWINE算法14轮多维零相关线性逼近

命题1[2]（线性映射的线性逼近相关度）对线性映射则利用此命题，可以得到TWINE的14轮（5-20）零相关线性逼近。

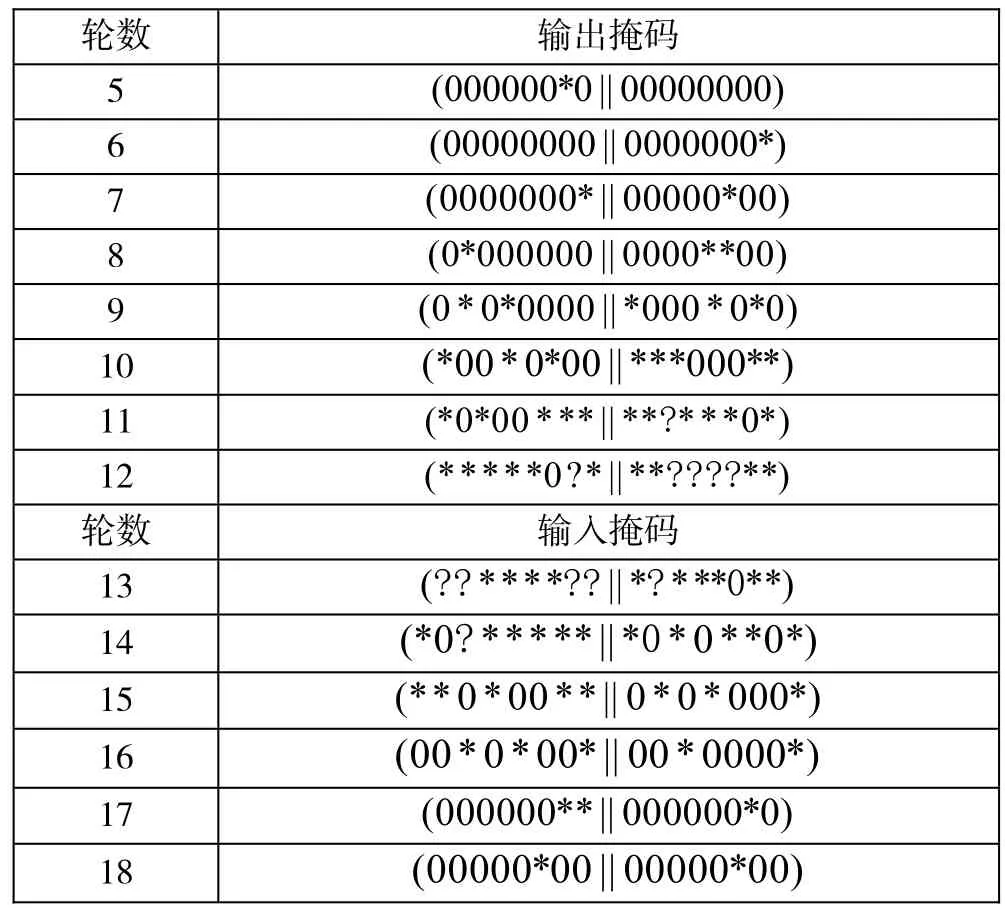
表4 TWINE算法的14轮零相关线性逼近

19 (*0000000||00000000)20 (00000000||00*00000)

其中，“0”表示0半字节值，“*”表示非0半字节值，“?”表示未知半字节值。选取第 5轮的输出掩码为第 20轮的输入掩码为从加密方向看，第12轮的输出掩码为则其左侧第5个半字节为0半字节；从解密方向看，第 13轮的输入掩码为其左侧第5个半字节为非0半字节 ，因此产生矛盾，则可以构造出一条 14轮零相关线性逼近：

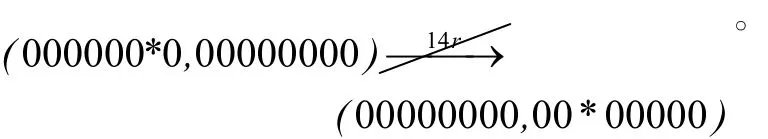
3 结语

本文主要评估了TWINE 密码算法关于多维零相关线性分析方法的安全性。首先构造了算法的等价结构，并由此构造了 14轮零相关线性逼近，之后对24轮的TWINE进行了多维零相关线性分析。分析其攻击结果可知TWINE对多维零相关线性分析是不安全的。其不足是此方法的数据复杂度明显高于其他方法，进一步研究将考虑通过分析算法的结构特点、密钥扩展算法等来降低其数据复杂度。

[1]Suzaki T, Minematsu K, Morioka S, et al. textnormal { extsc {TWINE}}: A Lightweight Block Cipher for Multiple Platforms[C]//Selected Areas in Cryptography. Springer Berlin Heidelberg，2013.

[2]BOGDANOV A, RIJMEN V. Linear hulls with correlation zero and linear cryptanalysis of block ciphers [J].Designs, Codes and Cryptography, 2014.

[3]BOGDANOV A, WANG M. Zero correlation linear cryptanalysis with reduced data complexity[C]// Proceedings of the FSE 2012, Washington, DC, USA, 2012.

[4]BOGDANOV A, LEANDER G, NYBERG K, et al.Integral and multidimensional linear distinguishers with correlation zero [C]// Proceedings of the ASIACRYPT 2012, Beijing.China，2012.