明清间管乐器的端口改正辨析

戴念祖

(中国科学院自然科学史研究所,北京 100190)

明清间管乐器的端口改正辨析

戴念祖

(中国科学院自然科学史研究所,北京 100190)

明代后期音乐家朱载堉对管乐器的端口做出改正,其改正的理论和数据都是正确的。入清以后,康熙帝做了同样的工作,但其理论和数据都错了。此后,科学家徐寿照抄康熙的结论,而晚清邹伯奇却退步到完全不做端口改正的地步。这是科学史上逐年退步的一个小小实例。

端口改正 朱载堉 康熙帝 徐寿 邹伯奇

在科学史上,曾有人认为管、弦同长同音。其实不然。由于气柱的惯性,它总要稍微溢出管端外,管音就比同长的弦音低一些。在相同张力和密度下,倍半弦线总是成八度音程,而倍半之同径管只有约略大七度。八度同径管,其长度比究竟多少？自明后期以降,音乐家和声学家对管端改正作了许多探讨。本文旨在梳理这一历史知识和技术。

1 朱载堉的端口改正

朱载堉曾多次作律管实验,“命工依彼围径皆同之说制管吹之,以审其音。林钟当与黄钟、太簇相和而不相和；南吕当与太簇、姑洗相和亦不相和,黄钟正半二音全不相应而甚疑焉。”[1]

“相和”、“相应”是指二音协和或二管发生共鸣或共振。朱载堉在此指出,同径管四度(林钟—太簇,南吕—姑洗)、五度(林钟—黄钟,南吕—太簇)、八度(黄钟正半)都不相和。朱载堉在疑惑之中进一步以实验指出：

以竹或笔管制黄钟之律一样两枚,截其一枚分作两段,全律、半律各令一人吹之,声必不相合矣。此昭然可验也。又制大吕之律一样两枚,周径与黄钟同,截其一枚分作两段,全律、半律各令一人吹之,则亦不合,而大吕半律乃与黄钟全律相合,略差不远。是知所谓半律皆下全律一律矣。[2]

引文中“全”与“半”是指倍、半长度。如,倍黄钟为2尺,正黄钟则为1尺；倍黄钟为1尺,正黄钟则为0.5尺。从倍黄钟到倍应钟的十二律称为“全律”,那么从正黄钟到正应钟的十二律就称为“半律”。余仿此。朱载堉在此指出,倍半长度的同径管不相和,相和者为下全律一律(表1)。

表1 朱载堉的等程弦律 (单位：尺)

由表1可见,在等程律中,“下全律一律”而相应者,即是,管律正黄钟1尺不与0.5尺半黄钟相应,而是与0.4719尺半大吕相应。余类推。在三分损益律的同径管中,如表2,按朱载堉说法,9寸正黄钟与4.21寸半大吕相应。余类推。

表2 三分损益弦律 (单位：寸)

2 康熙的改正理论及影响

康熙在其《御制律吕正义》上编卷2《明管音与弦音全半应声之不同》中对管端改正问题作出讨论。他说：

全弦半弦之音相应,而半律较全律则下一音。[3]

朱载堉的“下一律”被康熙改成“下一音”了。“下一音”就成了下二律。从表2可以看出,照康熙之见,同径管相应者为18寸倍黄钟与8寸正太簇,或9寸正黄钟与4寸的半太簇。他因此断论：

凡弦度无论长短,其全半声必相应。管律同径者,亦无论长短,其九分之四则声相应。[3]

康熙不仅篡改了朱载堉的实验结论,他还炮制了一个错误的理论。他说：

若夫正黄钟与半黄钟不相应者,取正黄钟管式平分之为半黄钟之度,其正黄钟九寸之度,自吹口至管底九分,九折而抵其一边者,值半黄钟之四寸五分而界于九分之四分、五分之间与界线所触,内周整分之度不合,是以其音不应。而半太簇之四寸,正值黄钟之九分之四,与界线相触,内周之第四分度恰合,故其声与正黄钟相应也。[3]

将这段文字换一种说法,人们就可以理解康熙之原意。若有9寸、4.5寸和4寸三种不同长度的同径管,设定管内振动着的空气柱波长为1寸,那么,9寸和4寸之管都可以被1寸波长量尽而成整数,独4.5寸不成整数。因此,9寸或4寸之管可以相应。或者说,两支同径管都是一个特定波长的整数倍时,该二管相应。康熙的这个理论是荒谬的。它与管内空气柱振动法则相距太远了。众所周知,管子长度不同,其发声频率也就不同,也即管内波长不同。怎么能预定一个特定波长衡量不同长度的管呢？

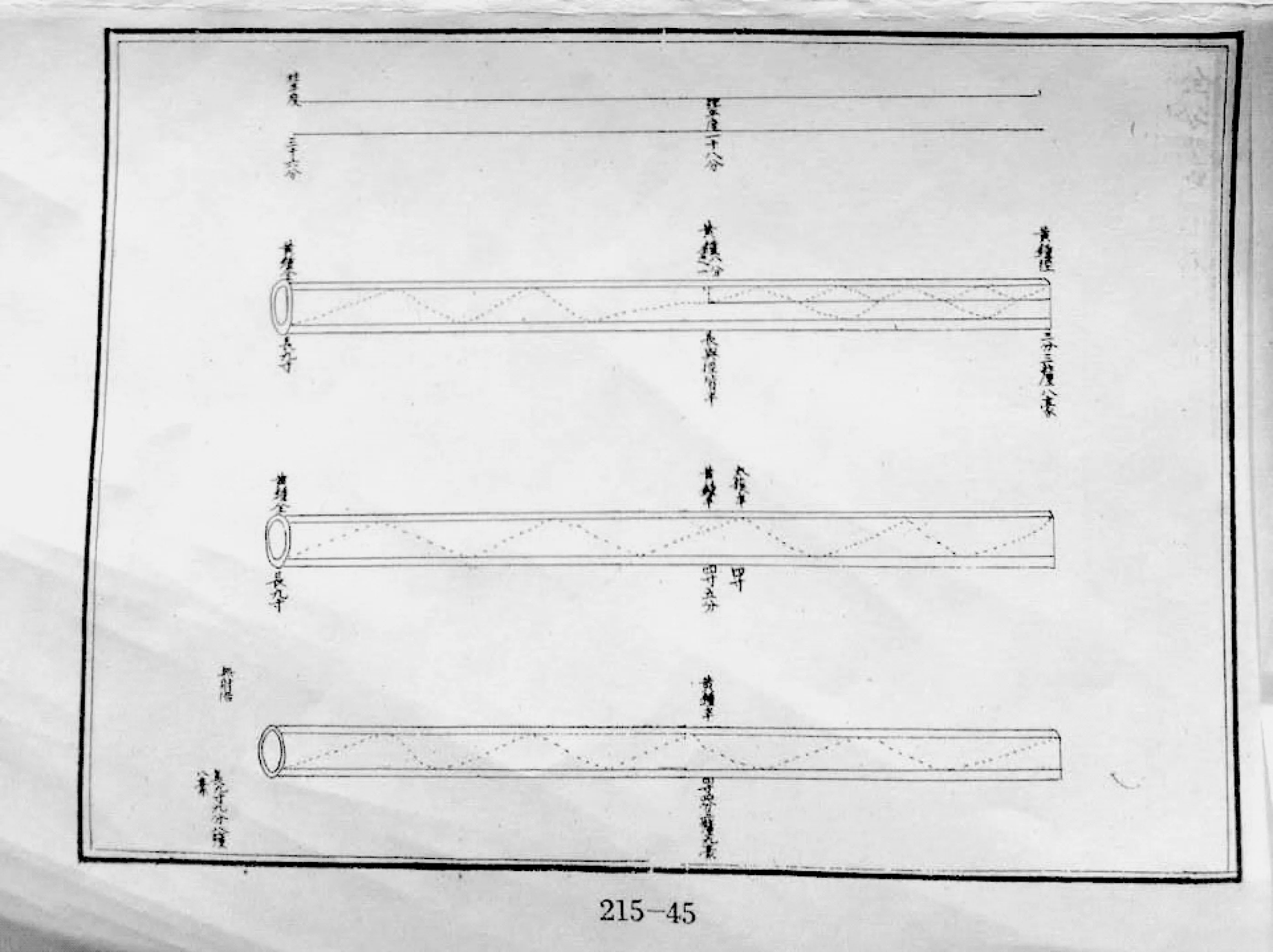
图1 《御制律吕正义》绘管内的“折”或“折数”图

事实上,康熙帝并无波长的概念。从其所绘图(图1)中不难看出,他理论中的“折”或“折数”充其量只能看作是1/4个波长。其绘图的随意性和错误一目了然。

然而康熙的错误却对徐寿产生了影响。徐寿(1818～1884),清末知名科学家。1878年,他在傅兰雅(John Fryer,1839～1928)主编的《格致汇编》(第三年·秋季刊)中发表《考正律吕说》一文。该文写道：

律管之制,以损益相生之数定之,与五声之高下相较,逐管依级数(此指“音级”——本文笔者注)而逐浊,故至半黄钟不与正黄钟相应。自古至今,当有论及者。然究不能发明其所以然。夫五声源有全级半级之分,乃天籁之自然。如宫至商为全级,而变宫至宫为半级,果能清浊相叶高下相宜者,无论何种乐器,尽皆如是。惟声出于实体者,正半相应,故将其全体半之而其声仍与全体相应也。至于空积所出声者,则正半不应。故将同径之管半之,其声不与全体相应,而成九与四之比例。古来相传,以弦音与管音相合,则宫应黄钟,羽应南吕,清宫再应半黄钟,如此而首音至八音之间自有全级半级之定位。但半黄钟既不能应黄钟,而弦音之清宫则与宫相应。两相龃龉,不相合之理显然。[4]

由此看来,徐寿知道,弦线(“实体”)正半长度相应,而管(“空积”)正半长度不应。他认为,同径管八度相应,则其管长之比为4∶9。这个结论显然是抄自康熙的《律吕正义》。徐寿本人对此未曾做过任何实验。康熙的错误被徐寿看作是“古来相传”的知识；徐寿心中所谓“自古至今,当有论及者”,显然指康熙帝。

徐寿的错误文章被来华传教士傅兰雅以讨教信的形式译成英文,并将它寄给了英国《自然》(Nature)周刊,作者也成了傅兰雅。1881年3月10日出版的《自然》周刊就以“中国声学”为题刊载了傅兰雅的来信。同时《自然》还加了编者按语。按语中指出：“看来,发现对旧定律(指弦管同长同律——本文笔者注)的真正有科学意义的现代修正却来自中国,并且以最原始的器具证明该修正是有根据的。”英国的声学家斯通博士(Dr.W.H.Stone)还为这封信写下短评。他说：“傅兰雅先生在他的观察报告中所持的意见是完全正确的”,“很有意思的是,证实这个鲜为人知的事实(指端口改正——本文笔者注)却是来自遥远的东方,而且是以如此简单的实验方法得到的。”[5]

为何一个错误的理论和数据会受到西方学界重视和表彰呢？因为当时的西方学界还在秉持弦、管同长同音的观念。正如物理学家廷德尔(John Tyndall,1820～1893)在其名著《声学》中称“半长管的音为全长管的八度”一样[6]。这个观念不仅大大落后于朱载堉,甚至落后于康熙。康熙毕竟还主张端口改正,即使其改正数据是错的。就技术上而言,要对管乐器做端口改正是完全正确的；就理论上而言,原本出自康熙的改正理论是错误的。遗憾的是,在19世纪下半叶,朱载堉却被人们遗忘了。

本文作者在其著《中国声学史》[7]中因未曾读到康熙的相关理论,而错将徐寿理论抬高了,谨此示读者。

3 邹伯奇的等比管律

邹伯奇(1819～1869)在其《邹徴君存稿·律数说》中列出一组等比管律的数据[8]。他以《史记·律书·律数》中列出“黄钟八寸七分”为正宫,以《吕氏春秋·仲夏纪·古乐》中列出的“三寸九分”为清宫,通过计算而得到一组等比管律(表3)。

表3 邹伯奇等比管律 (单位：寸)

表3中,公比数为q,

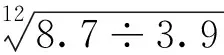
邹伯奇的理论计算并不误,其问题在于这组管律未有端口改正。除了黄钟与清黄钟两支管是正确的八度音程外,其余十一支管发音都是不准的。据八度管长之差可得端口改正为：

8.7÷2-3.9=0.45(寸)。

其余十一支管都要一一减去这个改正数。就管的端口改正而言,邹伯奇比其前、包括康熙在内的学问家都退步了。

1 朱载堉. 律学新说[M]. 卷1, 密率求周径第六//李天纲. 朱载堉集. 第4册. 上海: 上海交通大学出版社, 2013. 3184.

2 朱载堉. 律吕精义[M]. 内篇卷2, 不取围径皆同第五之上//李天纲. 朱载堉集. 第1册. 上海: 上海交通大学出版社, 2013. 331.

3 圣祖仁皇帝. 御制律吕正义[M]. 上编卷2, 明管音与弦音全半应声之不同. 四库全书本.

4 徐寿. 考证律吕说[J]. 格致汇编, 1878, 7.

5 A Chinese Acoustics[J].Nature, 1881, 23: 448～449.

6 Tyndall J.Sound[M]. Third Edition. London, 1875. 207～208.

7 戴念祖. 中国声学史[M]. 石家庄: 河北教育出版社, 1994.

8 邹伯奇. 邹徴君存稿·律数说[M]//中国科学技术典籍通汇·物理学. 第1册. 郑州: 河南教育出版社, 1995. 1065.

ABSTRACTThe musician Zhu Zaiyu (朱载堉) corrected the ends of wind instruments in the late Ming Dynasty, his theory and data being correct. In the Qing dynasty, the Kangxi Emperor composed a similar essay, though his theory and data were incorrect. In the 19thcentury, the scientist Xu Shou copied the conclusions of Kang Xi, and Zou Boqi retrograded to the step of the complete non-correction of ends. This is a small example of gradual retrogression in the history of science．

KeywordsCorrection of the ends of wind instruments, Zhu Zaiyu, Kangxi Emperor,Xu Shou, Zou Boqi

ADiscussionoftheCorrectionoftheEndsofWindInstrumentsintheMingandQingDynasties

DAI Nianzu

(InstitutefortheHistoryofNaturalSciences,CAS,Beijing100190,China)

N092∶O4- 092

A

1000- 0224(2017)03- 0316- 05

2017- 02- 20

戴念祖,1942年生,福建长汀人,研究员,主要研究方向为中国物理学史。