低冲分离装置引导阶段动力学建模与实验研究

陈，， ，

(1. 北京航空航天大学航空科学与工程学院，北京 100191 ；2. 北京大学湍流与复杂系统国家重点实验室，北京 100871)

低冲分离装置引导阶段动力学建模与实验研究

陈韬1，郭龙飞1，赵振1，刘才山2

(1. 北京航空航天大学航空科学与工程学院，北京100191；2. 北京大学湍流与复杂系统国家重点实验室，北京100871)

采用基于LZB碰撞模型的多刚体系统动力学的方法，建立了低冲分离装置引导阶段的动力学模型，设计了分离螺栓沿分离管道运动的引导阶段原理性实验平台，实验测量结果验证了模型的正确性。本研究为涉及复杂碰撞的低冲分离全过程动力学的研究奠定了一定理论和实验基础。

低冲分离；多点碰撞；LZB碰撞模型

Abstract：Based on LZB multi-impacts model for multibody system, a dynamic model focusing on the guiding process of low-shock separation was established. The effectiveness of the model was verified by experiments using high speed cameras. This study provides theoretical and experimental supports for the future development of the whole process of low-shock separation.

Keywords：Low-shock separation；Multiple impacts；LZB model

0 引言

分离装置属于航天工程中的关键部件，其可靠性直接关系到发射任务的成败。例如火箭或导弹的级间分离装置在分离时, 要保证两个分离部件可靠分离, 并确保分离过程中或分离之后，分离螺栓被安全捕获，从而消除影响正常飞行诸如多余物等危害因素。近年来，世界上多起卫星发射失败均与分离装置有关：1999年俄罗斯“呼啸号”的整流罩脱落；2003年日本发射间谍卫星的H2A火箭的助推器无法与芯级分离；2009年美国发射“嗅碳”卫星的运载火箭整流罩未能按程序与第三级火箭分离；2009年韩国 “罗老”号火箭升空后，卫星整流罩的一侧未能正常打开，导致卫星未能进入预定轨道。

当前，分离装置的设计大部分采用“经验设计—实验—修改”的方法，局限性较大。在设计初期，工程技术人员对分离装置工作机理缺乏系统的研究，多采用经验设计。在设计中，多通过大量实验来筛选参数，验证设计的可靠性。因此，设计需反复实验和修改，甚至重新设计，造成成本高，周期长。所以，采用理论建模与分析、数值计算与仿真和实验验证与识别等动力学的综合设计与优化方法，针对分离装置分离过程的动力学行为进行研究，有助于推进分离装置现代分析设计发展，具有极其重要的工程现实意义。目前，国内外学者已经对分离装置分离过程的动力学问题开展了一些研究。

分离装置作为研究对象始于Brauer，他第一次较系统地介绍了火工分离装置的原理、结构构成、所用材料特性及应用情况[1]。Bement[2]统计了23年中84起失败教训后总结到，之前没有把火工分离装置真正当作一种技术来研究，完全依靠手工经验，很少采取测试手段进行检验，缺乏标准的设计规程，进而导致分离装置的可靠性降低。

在动力学研究方面，Richter[3]、Gonthier等[4-5]和Kutschka[6]基于内弹道和空气动力学，对火工装置的起爆、燃烧等分离火工装置工作的运动规律进行数值仿真和模拟。张雪原等[7-8]对低冲分离装置驱动分离过程开展了冷气和热爆的动力学建模和实验研究。张宏剑等[10-11]采用多体动力学方法，将低冲分离装置分为释放、引导、捕获三个阶段进行研究。叶耀坤等[12]针对导弹级间分离系统的需要，设计了一种楔块式火工解锁螺栓，建立了其作用过程的内弹道模型，并进行了仿真计算和实验研究。Kuo等[13]和Goldstein等[14]采用大变形非线性有限元模拟火工装置瞬间切割分离的动力学过程。崔垚[15]设计了新型气压式分离解锁装置，建立了带有挠性部件的卫星和小卫星的分离平台，并且研究了卫星平台轨道运动受到此机构产生的冲击载荷的影响。

在分离装置的测试方面，爆炸分离冲击环境值得关注，它是引起飞行器故障的环境因素之一，密切关系到飞行器任务的成败[16]。因此模拟火工冲击并测量冲击响应是试验中的关键。Peter等[17]采用振动台和机械撞击方式模拟爆炸冲击环境。DeCroix 等提供了一种新的测试技术[18-20]，这项技术的激励源采用高压气炮来替代爆轰冲击波，以及安装在分离装置侧边的压力传感器测得测量腔内气压。张枫等[21]检验了某型飞机反尾旋系统中连接机身构架和反尾旋伞的低冲分离装置的试验性能指标。

某新型低冲击分离装置是一种分离螺母式的解锁装置，又称为分离螺母，如图1所示。采用螺纹连接,连接强度优于爆炸螺栓和其他解锁分离装置，结构尺寸小，无需拆卸即可重复使用，所需分离能量小，爆炸启动压力小，产生的分离冲击小，且无污染。分离螺母是目前国内外卫星、火箭上大载荷连接优先采用的分离装置之一。目前虽然出现很多非火工激发的新型分离装置[22-27]，但在可靠性方面还缺乏长期工程实际的检验。因此，火工低冲分离装置仍然在航空航天工程中的发射、在轨起飞以及返回对接的各个方面发挥着关键作用。

低冲分离装置在分离过程中的相互作用比较复杂，会受到火工装置化学能的释放，内部连接弹性部件预压势能的释放，以及机构间隙和摩擦等的联合作用，多个接触点同时存在，导致分离螺栓的动力学行为往往超出人们的预期，技术人员难以判断怎样的火工能级水平才能保证分离要求。技术人员在无法弄清分离动力学规律的情况下，尝试设计新的低冲分离装置，使其可靠性得不到提升。从目前掌握的资料来看，以往的研究主要集中在系统中火工释放装置上，未对释放过程动力学开展详细的研究，无法提炼出低冲分离装置机构的关键参数，也无法说明这些参数如何影响分离过程，如何设计才能够保证安全、可靠、同步性好以及冲击环境低的分离要求等问题。

当前虽然没有专门针对低冲分离装置螺栓从释放到捕获的动力学建模和分析的相关研究，但是可以借鉴多体动力学的建模方法，对这一阶段的动力学行为开展研究。本文以分离螺栓沿分离管道运动作为研究对象，开展理论建模、实验验证和敏感参数分析的探索性研究，为全过程的动力学建模奠定基础。

1 动力学建模

1.1 运动学描述

针对图1中分离装置引导阶段连接螺栓在分离管道中的运动，建立简化动力学模型,如图2所示。以分离管道的O点为原点建立直角坐标系Oxyz，在螺栓的质心(xC,yC,zC)建立随体坐标系Cx′y′z′，其中z′沿螺栓轴指向螺栓头方向。

两个坐标系之间变换采用卡尔丹角，即依次绕着x′、y′、z′轴的转角(α,β,γ)，从管道坐标姿态方位转动为螺栓的姿态方位。系统的广义坐标设为q=(xC,yC,zC,α,β,γ)T。系统的动能T可以表示为：

(1)

质量矩阵M可表示为

(2)

其中,

1.2 拉格朗日方程

利用拉格朗日方程，分离螺栓在分离管道的动力学方程可以表示为：

(i=1,2,…,6)

(3)

其中，Qi为非接触主动力的广义力，一般为重力引起的广义力。分离螺栓在分离管道中可能经历无接触、碰撞和接触等运动，碰撞接触可以在s个点同时发生。无接触时s=0，否则s>0。在接触点处建立局部坐标系，法线方向为n，两个切线方向为τ1和τ2。Fn,j、Fτ1,j、Fτ2,j分别是第j个接触点的接触力沿nj、τ1,j和τ2,j方向的分量。那么，方程(3)中接触力的系数矩阵可以表示为：

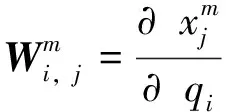
(4)

进而设螺栓上第j个接触点的速度vj，沿着局部坐标nj、τ1,j和τ2,j的分量为vn,j、vτ1,j和vτ2,j。

1.3 碰撞动力学的微分方法

当分离螺栓沿着分离管道运动时，碰撞不可避免，根据它们的几何形状，螺栓与管道可能的碰撞如图3和图4所示。碰撞过程采用Dobox-Keller提出的动力学的微分方法。

如果分离螺栓在接触点发生碰撞，由于碰撞力远大于常规力，常规力可以忽略。并且冲击过程非常短，碰撞过程中系统的位形假设不变，而是速度发生了突变。根据这些假设，动力学方程(3)可以简化为：

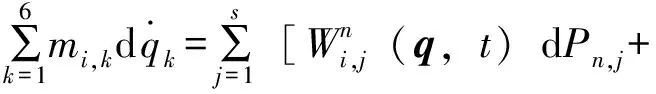
(5)

其中dP*=F*dt，P*为接触力对应的冲量。这里考虑了系统是定常的。

1.4 Coulomb摩擦定律

本文所搭建的原理性实验平台，分离管道内部是干燥的。因此假定：不管接触还是碰撞过程中，法向接触力与切向接触力之间都满足Coulomb摩擦定律。

当螺栓与管道接触点的切向相对速度vτ,j≠0，接触力的切向摩擦力分量和法向分量的大小满足比例关系：

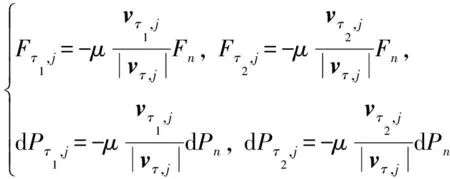
(6)

其中第1列方程适合接触过程，第2列等式适合碰撞过程。

当接触时切向速度vτ,j=0，接触点切向速度为0(黏滞或滚动)可能保持一段时间，也可能反向滑动。如果能够保持黏滞，约束采用速度的全导数为0(考虑接触点的变化)的方程。同时，接触力须在摩擦锥之内，否则，滑动继续，摩擦力与法向接触力的大小仍然满足比例关系。

如果保持黏滞，

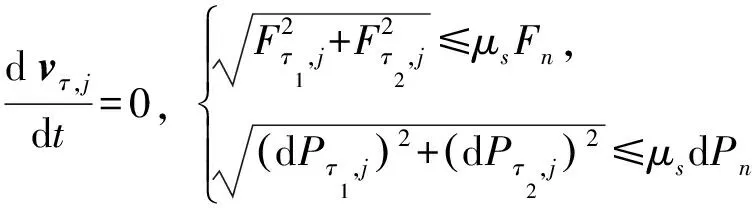
(7)

如果继续滑动，

(8)

1.5 接触时的不可刺穿条件

接触时的法向接触力采用刚体间不可压缩条件确定。当螺栓上的接触点j沿着导向管道内面运动时，接触点的法向速度满足vn,j=0。如果一直接触，法向速度为0能够保持，法向速度对时间的全导数为dvn,j/dt=0，这时法向接触力Fn,j≥0；如果接触不能保持，接触也不可能刺穿，dvn,j/dt>0，接触力Fn,j=0。因此，接触力采用下面的互补条件获得。

(9)

1.6 冲击时的冲量分配律

如果螺栓与管道内壁的碰撞发生在一个点上，仅采用式(5)～式(8)，以接触点的法向冲量为自变量，就可以求碰撞的演化过程。但是当螺栓一端与管壁接触，另一端发生碰撞如图3所示，两点碰撞便发生了。对于多点同时碰撞问题，采用Liu C S等提出的冲量分配律(Impulsive distributional law)也称为LZB模型[28-37]来解决。

对j个碰撞点，可以引入一个法向接触模型

Fn,j=Kj[δj(q,t)]ηj
(j=1,2)

(10)

根据式(10)，接触区域如同添加了一个法向的非线性弹簧，弹簧变形、弹簧的势能以及法向接触力三者之间是一一对应的关系。这样，可以建立任意两个接触点法向接触力之间的比值，这一比值可以化为局部法向弹性势能比和接触刚度比的函数关系。即利用式(10)可以推导出：

(11)

(12)

其中En,j为j点的法向累积势能，代表式(11)括号中的所有项。式(12)给出了法向冲量的增量之间的关系，称为冲量分配率。

不管多点碰撞还是单点碰撞，碰撞过程可以采用式(5)～式(8)，再加上冲量分配比式(12)获得冲击的演化过程，但是冲击后的能量耗散情况并没有体现，也就是冲击结束的条件并没有给出。下面采用Stronge的能量恢复系数给出冲击过程中的能量耗散。Stronge 定义的能量恢复系数为：

(13)

其中Wr,j为j点碰撞恢复阶段螺栓对管壁沿法向做的功，而Wc,j为压缩阶段螺栓对管壁沿法向做的功。由于Wr,j和Wc,j正负相反，为了保证恢复系数的平方为正，式(13)等号右边加了一个负号。压缩阶段和恢复阶段的分界点为vn,j=0。式(13)实际上与法向累积势能En,j建立了联系。

本文采用Stronge的恢复系数对碰撞过程的能量损失进行描述。在碰撞过程中, 只要任意一对碰撞点在恢复阶段做的功与其在压缩阶段做的功的比值能够满足式(13), 便能判断这一对点处的碰撞终止。要对整个多点碰撞的终止进行确认，须所有碰撞点都满足能量恢复系数，即碰撞全部结束。根据上述判断标准，系统在某些碰撞点可能发生二次碰撞，即多点碰撞过程中某些点的碰撞可能会重新开始。因此，LZB方法不仅能够正确反映碰撞点切向的复杂微运动，也能正确反映接触点法向的复杂的多次碰撞行为。

2 实验研究

2.1 实验平台

本文针对分离装置引导阶段，进行了螺栓沿透明管道运动的实验研究。实验简化了分离装置的复杂结构，利用无接触测量捕捉碰撞动力学行为。实验原理图和实验现场如图5(a)和图5(b)所示。亚克力管水平安放在实验台上，尼龙螺栓被激发沿着透明的玻璃管道运动，由于初始速度和重力的原因，螺栓与管道产生接触与碰撞。高速摄像机清楚地记录了螺栓沿管道运动的整个过程。图5(c)显示螺栓上贴有黑白相间的标记点，高速度摄像机通过追踪这些标记点，获得螺栓详细的运动信息。

实验测量装置采用高速摄像机测量管道中螺栓的运动。控制电脑安装了自动跟踪识别的Davis软件，以及Motion Studio位移、速度分析软件；照明器材采用3台800W的无闪频摄影灯。

螺栓和亚格力管的几何尺寸如表1和表2所示，各尺寸含义见图6所示，高速摄像机的参数如表3所示。

表1 螺栓的几何尺寸Tab.1 The geometric parameters of the bolt

表2 管子的几何尺寸Tab.2 The geometric parameters of the channel

表3 摄像机关键参数Tab.3 The keyparameters of the camera

2.2 实验与仿真对比

用一台高速摄像机记录二维的运动信息。实验经过数次的筛选以确保螺栓沿管道在竖直平面内运动。由于重力的作用，螺栓下部的3个点容易与管道内壁碰撞，分别标记为E、P、D，如图6所示。

通过实验图像及数据可知，螺栓与管道壁之间发生了3次碰撞，其中3次实验碰撞的时间分别为：0.06462s、0.08308s、0.09231s，3次碰撞时螺栓的位置如图7(a)、(b)和(c)的上图所示，3幅图像分别对应螺栓上E点、D点与P点和圆管内壁底部碰撞。

根据几何关系，实验跟踪点的数据可以换算得到E、D、P这3个点的位移变化曲线，同时通过仿真也求出这3个点的速度变化曲线，然后与计算仿真得到的曲线进行对比。可得到如图8、图9和图10所示的对比图像。其中红色表示仿真曲线，蓝色表示实验曲线。从D、E、P这3点的实验与仿真对比图可以看出，实验曲线和仿真曲线基本上吻合。观察3个点y方向的位移图像，3个点的最大实验位移都能够达到46mm(图8、图9和图10中的(b)图)，管子在底部到固定坐标原点的距离上也在46mm左右，说明3个点都存在碰撞的情况，并且3个点各碰撞了一次，碰撞时间分别为：0.0633s、0.08178s和0.09299s，仿真得到的碰撞时间点与实验结果对比相差不到0.001s。经过模型计算的3个碰撞点的位形如图7的(a)、(b)和(c)的下图所示，与上图的实验对比位形相同。因此，实验和仿真不管从时间上还是从空间上的对比，结果都是一致的。

为了更全面地了解螺栓的运动，通过对实验数据进行处理，换算得到螺栓的质心轴向和径向位移曲线以及转角曲线，即螺栓的3个广义坐标的时间历程，如图11和图13中的(a)图所示。进一步差分得到相应的速度如图11、图12和图13中的(b)图所示。同时把实验结果(蓝色曲线)与仿真结果(红色曲线)进行对比，质心运动的实验和仿真结果吻合得很好。

另外，注意到轴向速度(图11(b))和角速度(图13(b))在相邻碰撞之间的仿真曲线都是一条水平的线段，也就是说加速度为0，实验曲线也基本接近平行，这与螺栓在自由飞行时轴向上的受力为0，并且也不受任何力矩作用的事实相吻合。说明实验数据是合理的。而径向速度在相邻碰撞之间的仿真曲线都是平行的斜线段，实验曲线也是这样。这与螺栓在自由飞行时竖直方向只受到重力的作用、加速度为恒定的重力加速度的事实吻合。图14给出了轴向加速度的实验和仿真曲线对比曲线，可以看出螺栓自由飞行时的轴向加速度都处在9.8m/s2附近的范围内，符合物理事实，从而验证了实验数据是可靠的。

综上所述，模型的仿真算例能够很好地反映实验结果，从而验证了模型的正确性，同时实验结果的分析也进一步证明了实验数据的可靠性。

3 结论

低冲分离装置从分离到捕获是一个复杂动力学过程，全过程含有大量的接触、碰撞与摩擦等非光滑和非线性因素。本文以低冲分离装置引导阶段的螺栓运动为研究对象，首先，采用基于LZB模型的非光滑多体系统动力学方法建立了其动力学模型，设计并搭建了实验平台，开展了相应的实验研究，并将模型的计算结果与实验测得的数据进行了对比，结果非常吻合。说明基于LZB多点碰撞模型的多体动力学方法能够充分把握分离螺栓引导阶段的动力学特征。本文的探索性研究为低冲分离装置全过程动力学的建模奠定了理论和实验基础。

[1] Brauer K O. Handbook of pyrotechnics[M]. Chemical Publishing Company, 1974:1-50.

[2] Bement L J. Pyrotechnic system failures: causes and prevention[J]. NASA Technical Memorandum 100633,1988.

[3] Richter R.Theory of a pyrotechnically driven device[R]. JPL Invention Report, NP0-17117/6631, 1989.

[4] Gonthier K A, Powers J M. Formulation, predictions,and sensitivity analysis of a pyrotechnically actuated pin puller model[J]. Journal of propulsion and power, 1994, 10(4): 501-507.

[5] Gonthier K A, Kane T J, Powers J M. Modeling pyrotechnic shock in a NASA standard initiator driven pin puller[R]. AIAA 1994-3054,1994.

[6] Kutschka J. Pyrotechnically actuated mechanism performance prediction and test correlation[R]. AIAA 2000-3513, 2000.

[7] 张雪原，唐文彦.低冲击分离装置冷气驱动分离过程的动力学建模与试验[J]. 固体火箭技术,2008, 31 (5):435-438.

[8] 张雪原, 唐文彦. 支撑角对低冲击分离装置分离过程影响动力学仿真[J]. 固体火箭技术, 2009, 32(1): 20-22.

[9] 张宏剑, 庄方方, 季宝锋,等. 运载火箭分离装置引导与捕获过程非光滑动力学研究[J]. 导弹与航天运载技术, 2015(3):30-33.

[10] 张宏剑, 庄方方, 曲展龙,等. 航天分离装置引导阶段非光滑动力学快速分析方法研究[J]. 北京大学学报(自然科学版), 2016, 52(4):717-721.

[11] 叶耀坤, 严楠. 低冲击火工解锁螺栓的内弹道特性分析[J]. 北京工业大学学报, 2012, 38(9): 1332-1336.

[12] Kuo J, Goldstein S. Dynamic analysis of NASA Standard Initiator driven pin puller[R]. AIAA 93-2066,1993.

[13] Goldstein S, Lu Y M, Wong T E. Importance of enhanced test data for computer modeling of exposively actuated devices[R].AIAA 1995-2852, 1995.

[14] 崔垚. 航天器低冲击分离控制技术研究[D]. 哈尔滨：哈尔滨工业大学,2013.

[15] Bement L J, Multhaup H A. Determining functional reliability of pyrotechnic mechanical devices[J]. AIAA Journal, 1999, 37(3): 357-363.

[16] Barrett P, Cornford S L, Larson C N, et al. Pyroshock testing using large resonant plates and SRS theory using time and frequency domain methods[C].Aerospace Testing Seminar, 17th, Manhattan Beach, CA. 1997: 101-109.

[17] DeCroix M, Quintana D, Burnett D, et al. Investigation of actuation dynamics in an explosively actuated valve using a gas gun[R]. AIAA 2005-4036, 2005.

[18] Tafoya J M, Burnett D J, Decroix M E, et al. Experimental validation of gas gun to evaluate components of explosively actuated valves[R]. AIAA 2005-4038, 2005.

[19] Tafoya J M, Tafoya J I, Inbody M A, et al. Pyrovalve function testing using gas gun actuation[R]. AIAA 2007-5140,2007.

[20] 张枫, 杨树彬, 杨安民, 等. 一种低冲击分离螺栓的设计[J]. 火工品, 2006 (3): 14-17.

[21] Lucy M H, Hardy R C, Kist, et al. Report on alternative devices to pyrotechnicson spacecraft[R]. 10thAnnual AIAA/USU Conference on Small Satellites, 1996: 1-19.

[22] Smith S, Dowen D, Fossness E, et al. Development of shape memory alloy (SMA) actuated mechanisms for spacecraft release applications[C].13thAIAA/USU Conference on Small Satellites, SSC99-XI-7.

[23] Fosness E R, Buckley S J, Gammill W F. Deploymentand release devices efforts at the air force research laboratory space vehicles directorate[C].AIAA Space 2001 Conference and Exposition, Albuquerque, NM. 2001.

[24] Peffer A, Denoyer K, Fosness E, et al. Development and transition of low-shock spacecraft release devices[C].Aerospace Conference Proceedings, IEEE, 2000,4: 277-284.

[25] Fosness E R, Buckley S J, Gammill W F. Deploymentand release devices efforts at the air force research laboratory space vehicles directorate[C].AIAA Space 2001 Conference and Exposition, Albuquerque, NM. 2001.

[26] Lan W, Brown J, Toorian A, et al. CubeSat development in education and into industry[J]. Aerospace Engineering, 2006, 805: 756-5087.

[27] Liu C S, Zhao Z, Brogliato B. Frictionless multiple impacts in multibody systems[J]. Proceedings of Royal Society A, 2008, 464: 3193-3211.

[28] Liu C S, Zhao Z, Brogliato B. Frictionless multiple impacts in multibody systems. II. Numerical algorithm and simulation results[C].Proceedings of the Royal Society of London A: Mathematical, Physical and Engineering Sciences. The Royal Society, 2009, 465(2101): 1-23.

[29] Liu C S, Zhao Z, Brogliato B. Variable structure dynamics in a bouncing dimer[D]. INRIA Research, 2008.

[30] Zhao Z, Liu C S, Brogliato B. Energy dissipation and dispersion effects in granular media[J]. Physical Review E, 2008, 78(3): 031307.

[31] Zhao Z, Liu C S, Brogliato B. Planar dynamics of a rigid body system with frictional impacts. II. Qualitative analysis and numerical simulations[C].Proceedings of the Royal Society of London A: Mathematical, Physical and Engineering Sciences. The Royal Society, 2009, 465(2107): 2267-2292.

[32] Liu C S, Zhang H, Zhao Z, et al. Impact-contact dynamics in a disc-ball system[C]. Proceedings of Royal Society A, The Royal Society, 2013, 469(2152): 20120741.

[33] Wang J, Liu C S, Ma D. Experimental study of transport of a dimer on a vertically oscillating plate[C].Proceedings of the Royal Society of London A: Mathematical, Physical and Engineering Sciences. The Royal Society, 2014, 470(2171): 20140439.

[34] Zhao Z, Liu C S, Ma D. Pure rotation of a prism on a ramp[C]. Proceeding of Royal Society A. The Royal Society, 2014, 470(2169): 20140007.

[35] Zhao Z, Liu C S,Zhang H. From line impact to rolling resistance[C]. Thematic Conference on Multibody Dynamics, Barcelona Spain, 2015.

[36] Jia Y B, Mason M T, Erdmann M A. Multiple impacts: a state transition diagram approach[J]. The International Journal of Robotics Research, 2013, 32(1): 84-114.

DynamicalModelandExperimentalStudyofLow-shockSeparationDevice

CHENTao1,GUOLong-fei1,ZHAOZhen1,LIUCai-shan2

(1.SchoolofAeronauticScienceandEngineering,BeihangUniversity,Beijing100191,China;2.StateKeyLaboratoryforTurbulence&ComplexSystems,PerkingUniversity,Beijing100871,China)

TJ450.1

A

2096-4080(2017)03-0044-10

2017-07-25；

2017-09-08

国家自然科学基金资助项目(73010801)

陈韬(1993-)，男，博士，主要研究方向为多体动力学。E-mail:616545414@qq.com