基于网格维数法的剑川县应急避难场所演化特征研究
2017-10-11王培茗陈宣先
刀 认,王培茗,方 硕,陈宣先
(云南大学 建筑与规划学院,云南 昆明 650504)
基于网格维数法的剑川县应急避难场所演化特征研究
刀 认,王培茗,方 硕,陈宣先
(云南大学 建筑与规划学院,云南 昆明 650504)
采用分形理论中的网格维数法对1985、2000、2014年三个时期剑川县主城区应急避难场所的空间分布特征及相关维数进行测算,得出应急避难场所不同时期空间分布的容量维和信息维。研究发现:(1)剑川县城市应急避难场所的空间演化由集中分布逐步向均衡分布发展;(2)剑川县城市应急避难场所空间分布经历了由不符合分形结构特征到完全符合分形结构特征的过程。
应急避难场所;网格维数;演化;剑川县城
0 引言
由于自然灾害频发,自古以来各国城市规划和建设者就很注重城市防灾问题,城市内部应急避难场所的建立对减少城市灾害损失、保护市民生命财产安全起到了重要作用。
但应急避难场所的形成和演变是一个十分复杂的问题,有其自身的规律和特点。目前虽然有关应急避难场所的研究成果较多,但主要集中于定性研究[1-2],定量研究主要是集中于对其分布现状评价及布局优化的研究[3-5],对其形成发育及演化特征的研究均未涉及。本文将以云南省剑川县为例,运用网格维数等分形方法对小城镇应急避难场所演化过程及演化特征进行研究。
1 研究区概况
剑川县位于云南省西北部,大理州北部。县域内地质构造复杂,断裂带交汇,断裂活动活跃,剑川县城地处下关—剑川地震带,抗震设防烈度为VIII度。据从公元886年至今的不完全统计,剑川县发生5~5.9级地震8次,6~6.9级地震5次,为大理州发生5级以上地震次数最多的县份之一[6]。本研究选取剑川县城1985、2000、2014年三个年度建成区内的应急避难场所为研究对象,探索其发生、发展、变化的特征和原因。
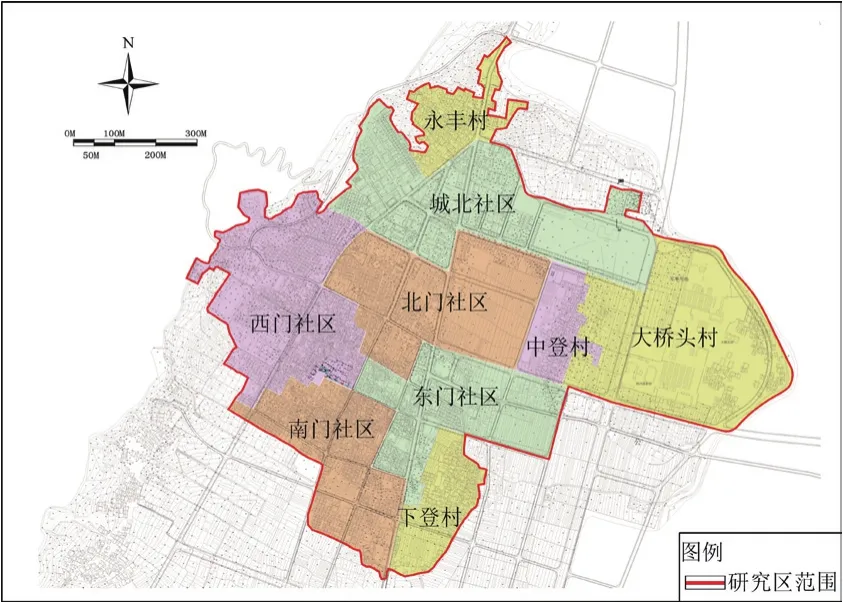
图1 研究区范围Fig.1 The study area
2 数据来源及研究方法
2.1 数据来源
本文数据主要源于云南省测绘地理信息局以及剑川县规划局所提供的1985、2000、2014年的建川县主城区地形图以及各个应急避难场所信息。
2.2 研究方法
本文选用网格维数测算法来分析应急避难场所系统空间分布的分形特征。网格维数法是分形理论中测算区域内的研究对象空间分布均衡程度的一种方法。该方法首先需要测算其容量维和信息维,容量维和信息维值变化于0~2之间, 正常情况下为1~2, 分维值的大小反映了研究区研究对象空间分布的均衡程度。相对应急避难场所系统而言,D值越大表明应急避难场所系统的空间分布越均衡, 反之则越集中[7]。
算法如下:
用边长为r的矩形将整个研究区域覆盖,不断将矩形的边长等分,并进行如下定义:

式中,Sij表示研究区域内应急避难场所出现在网格第i行、第j列的概率;
Nij(r)为表示网格第i行、 第j列落入的应急避难场所的个数;
N(r)则定义的是应急避难场所总共的个数。
根据信息论的原理,将应急避难场所系统空间分布的信息熵定义为:

若某年应急避难场所空间分布的泛方程满足:

则证明该年研究区内的应急避难场所系统空间结构是自相似的,且符合分形结构的特征,并满足:I(r)∝r-D。其中,D就是衡量应急避难场所空间分布均衡性的网格维数。
具体地说, 当D→0 时, 应急避难场所的分布集中到一条带状区域, 如沿河流、公路沿线分布, 这种情况在应急避难场所发展的初期可能出现, 当应急避难场所发展到一定程度时则较少出现; 当D→2 时, 表明研究区应急避难场所在各地区之间的空间分布越均衡。
3 研究区应急避难场所演化特征研究
3.1 1985、2000、2014年研究区应急避难场所空间分布演化过程
1985年是剑川县应急避难场所的发展起步阶段,截止至1985年底,剑川县有应急避难场所15个,空间分布如图2所示,此时的应急避难场所一般是将原有具有应急能力的空旷场地进行改造,改造力度相对较小。

图2 1985年研究区应急避难场所分布图Fig.2 Space distribution of emergency shelters in research area in 1985
从2000年开始,剑川县城市建设进入了快速发展阶段,应急避难场所的发展速度也惊人,从原来的15个应急避难场所发展到了2000年的29个,空间分布如图3所示,新增的应急避难场所主要集中在老城区周围,弥补了老城区应急避难场所不足的问题。但在剑川县古城内部,道路曲折、狭窄,不利于避震疏散,且建筑密度高,建筑质量差,应急避难场所较为缺乏的状况仍未得到改善。在2000版《剑川县总体规划修编》中,对此问题提出改进措施,剑川县新城区建筑物按VIII度设防,住宅建筑层数不超过4层,间距不得低于1:1.2,在小区内安排公共绿地和活动场地作为震时的临时避震疏散场地。在新城区内开辟广场、体育场、公共停车场、农贸市场、公共绿地等场地作为避震疏散场地;并选择适宜场地作为直升飞机起落场。并应对剑川古城内的建筑进行质量鉴定,对质量不符合抗震要求的进行抗震加固,在古城中拆除部分建筑(不符合古城保护规划要求的新建筑或质量很差又没有保留价值的建筑),按片儿留出避震疏散场地。

图3 2000年研究区应急避难场所分布图Fig.3 Space distribution of emergency shelters in research area in 2000
2000年至2014年,是剑川县应急避难场所发展的成熟时期,此时的应急避难场所除了数量上的增多,在自身的发展上也有了明显的成果。2014年,剑川县应急避难场所的数量增至59个,空间分布如图4所示。相对于2000年,剑川县应急避难场所的空间分布更为紧凑和密集,辐射范围更加广,发展更为成熟。2013版的《剑川县总体规划》中提出剑川县主城区要按VIII度地震烈度设防。规划还提出要在新城区内开辟广场、体育场、公共停车场、农贸市场、公共绿地等人流疏散场地。

图4 2014年研究区应急避难场所分布图Fig.4 Space distribution of emergency shelters in research area in 2014
3.2 研究区应急避难场所空间分布网格维数测算
为了对剑川县应急避难场所空间分布的分形特征进行实证研究,借助ARCGIS软件分别将1985、2000、2014年剑川县应急避难场所的空间分布图构建在网格图上,对研究区应急避难场所空间分布信息进行网格维数的测算。不断的将网格图的边界进行等分,当边界被等分到k份时,这个网格图将会被大小相等的k2个网格所占据,由此可以很容易的得出每个大小相等的网格边长为r=1/k。为了计算方便,我们将k按照2的倍数去改变大小,随着k值的有序变化,内部落有应急避难场所的网格的数目即非空网格的数目N(k)在不断地变化,与之发生相应变化的还有每个网格内部出现的应急避难场所的数量Nij(k)。每变化一个k值,就将相应的N(k)值和Nij(k)值记录下来,同时计算出每个k值对应的I(r)值,这样就会得到一个记录有k值及与之相对应的N(k)值、Nij(k)和I(r)值的表格。然后对表格中的数据进行拟合计算,本文运用[k,N(k)]点列拟合的直线斜率来计算应急避难场所空间分布的容量维数,用 [ln(1 /r),I(r)]双对数点列拟合直线斜率来计算应急避难场所空间分布的信息维数。
对 1985 年点列 [lnk,lnN(k)]、 [ln(1 /r),I(r)]进行回归拟合, 发现 1985年剑川县应急避难场所空间分布的容量维和信息维的散点图在拟合过程中虽然都出现了直线段,其二者拟合的直线段的斜率都小于1,说明此时应急避难场所空间分布的容量维数和信息维数都小于1,且还出现信息维数大于容量维数的情况。说明此时研究区范围内应急避难场所空间分布并不具备分形特征。
分别对2000年及2014年点列[lnk,lnN(r)]、 [ln(1 /r),I(r)]进行回归拟合,得出能反映2000年及2014年剑川县应急避难场所空间分布容量维数和信息维数的点列图拟合结果,如图5所示。
从信息熵散点图和容量维散点图的比较来看, 信息熵散点图相对容量维散点图在无标度区内线性拟合方程的拟合优度略高, 其根本原因是用“标度变换法”计算容量维时只统计有多少尺度为r(或1 /k) 的网格中有应急避难场所的分布 , 而有多少个应急避难场所落入该网格中则不再考察范围。而在计算信息维时却特别注重考察应急避难场所落入尺度为r(或1 /k)的网格中的概率大小, 这个概率实际上就是通过统计落入尺度为r(或1 /k)的网格中的应急避难场所个数来计算的。这就决定了容量维和信息维不相等,且一般情况下信息维散点图的拟合程度要高于容量维散点图的拟合程度。

图5 2000年及2014年应急避难场所空间分布容量维和信息维Fig.5 Space distribution capacity dimension and information dimension of emergency shelters in 2000 and 2014
用统计软件SPSS进行线性回归分析, 发现2000年和2014年剑川县应急避难场所空间分布无论是其容量维数还是信息维数的点列图拟合效果都很好,且2014年优于2000年,并伴随有无标度区的出现,经分析后分别得到每年无标度区范围内容量维和信息维的拟合方程。如表1所示:

表1 剑川县主城区应急避难场所2000年、2014年容量维与信息维的拟合方程
从上表中可以看出,发现其无论是非空网格数或是信息熵与k构成的对数拟合直线斜率,即2000年和2014年应急避难场所空间分布的容量维值和信息维值二者皆在大于1,且2000年拟合度大于0.92,经调整后更是大于0.93,2014年拟合度大于0.98,超出2000年的0.93。说明2000年变量非空网格数的对数及每个网格中出现应急避难场所概率的对数所产生的变异有93%是由变量k取值的对数引起的,2014年变量非空网格数的对数及每个网格中出现应急避难场所概率的对数所产生的变异有98%是由变量k取值的对数引起的,且拟合优度都相当大。结果证明研究区内应急避难场所的空间分布在2000年基本具备分形结构特征,2014年已经具备良好的分形结构特征。
3.3 1985、2000、2014年研究区应急避难场所的空间分形结构演化
从以上分析可知,剑川县应急避难场所的空间分布在不同时段的容量维和信息维出现的无标度区范围变化不大, 但是容量维维数和信息维维数呈现出递增趋势, 说明应急避难场所在研究区范围内的空间分布变得越来越均衡,这也与实际情况完全吻合。1985年剑川县城主城区内应急避难场所数量较少,经测算虽然其容量维数和信息维散点图有一定规律,即部分区间通过SPSS进行拟合可以得到直线段,但是容量维散点图与信息维散点图在部分区间拟合出现的直线段斜率均小于1,且信息维数值还大于容量维数值。结果说明在该时段内剑川县主城区应急避难场所的空间分布尚不符合分形特征,即其分形结构尚未形成。之后,选取2000年与2014年两个时间节点再次对剑川县主城区应急避难场所空间分布进行分形测算,经过网格维数测算法的测算,发现其无论是非空网格数或是信息熵与r构成的对数拟合直线斜率,即应急避难场所空间分布的容量维值和信息维值二者皆在1~2之间变动,且前者大于后者,并伴随着无标度区的出现。测算结果显示,该时段内剑川县主城区应急避难场所的空间分布符合分形特征,即其分形结构已经形成。应急避难场所空间分布状态的变化,可由容量维数和信息维数的变化来说明。容量维数和信息维数越接近2,说明应急避难场所空间分布越均衡。1985年至2014年两个维数的不断递增,说明了剑川县应急避难场所的空间分布由相对集中向均衡分布变化。1985 年以前, 剑川县应急避难场所主要集中在老城区域,呈现出十分集中的态势; 1985—2000年, 应急避难场所得到进一步发展, 应急避难场所的分布向老城北部的新城区扩散;2000—2014年,应急避难场的扩散方向有所转变,由之前的向老城区北部扩散转变为向老城区东部扩散。除此之外,老城区内的应急避难场所也得到了进一步的完善和补充。
4 1985、2000、2014年研究区应急避难场所空间演化特征
1985年是剑川县应急避难场所建设的起步年,存在着应急避难场所数量少,分布不均,且辐射范围较小,我们将1985年应急避难场所的空间发展特点概括为应急避难场所单体数量少,质量高,辐射范围较小,空间分布较为集中。
2000年剑川县应急避难场所的发展已初具规模,主要是围绕老城区发展,且空间分布密度较大。较之1985年,辐射范围的广度增强了许多,从老城内部发展到老城周边,这是由于从1985年到2000年,剑川县建设主要集中在老城区周围,使得应急避难场所的数量有了明显的上升,使得应急避难场所的空间分布密度、广度都有了显著的提高。
2014年的剑川县应急避难场所的空间分布辐射范围更加广阔。这是由于应急避难场所的数量进一步增加、每个应急避难场所自身的空间范围也在迅猛发展。从2000年到2014年,应急避难场所经历了发展的成熟时期,由原本的“点”向“面”的模式发展。这样空间上的显著变化,使得应急避难场所的辐射范围有了明显的提升,剑川县59个应急避难场所几乎辐射了剑川县整个主城区。其次,空间分布密度更为均匀。原本应急避难场所的密度是在新城区分布密度较大,而在古城区分布密度较小。而随着2000年至2014年城市经济发展迅速、城镇人口迅猛增长,政府加大了应急避难场所的修建力度,应急避难场所在整个城区的分布密度更为均匀,分布也更加密集。最后,2014年剑川县应急避难场所较之前单体空间扩展显著,横向空间扩展和纵向空间扩展互相结合,联动发展,使得应急避难场所的单体空间范围有了显著的提升。
5 结论
应急避难场所是目前学术界一项热门的研究议题。本文采用GIS空间分析的手段,以及分形学的网格维数和显著性水平分析法,对剑川县应急避难场所的分形发育及演化特征进行研究,得出剑川县城市应急避难场所的空间分布由集中分布逐步向均衡分布发展,且空间分布经历了由不符合分形结构特征到完全符合分形结构特征这样一个过程。通过研究城市的演化特征,将有助于充实我国应急避难场所研究的理论发展。
[1] 张敏.国外城市防灾减灾及我们的思考[J].规划师,2000,16(2):101-104.
[2] 齐瑜.北京市应急避难场所规划与建设[J].中国减灾,2005(3):34-36.
[3] 周晓猛,刘茂.紧急避难场所优化布局理论研究[J].安全与环境学报,2006,6(S1):118-121.
[4] 刘樱,王培茗,施益军.基于随机聚集维数的云南省峨山县城防灾空间布局评价研究[J]. 防灾减灾学报,2014(3):5-10.
[5] 徐波,关贤军.城市防灾避难空间优化模型[J].土木工程学报,2008,41(1):93-98.
[6] 闵子群, 沈斯伟.886—1981年云南地区M≥4.7地震目录[J].地震研究,1983(4):129-146.
[7] 刘继生,陈彦光.城镇体系等级结构的分形维数及其测算方法[J].地理研究,1999,17(2):82-89.
Abstract:This dissertation uses a fractal measurement method of grid dimension to measure the distribution features and the relevant dimensions of Jianchuan shelters' spatial distributions in 1985,2000 and 2014.Through the use of this method, the capacity dimension and the information dimension of the shelters' spatial distributions in three study years are also measured. The conclusions are:(1) There has been a shift in the spatial distribution of the shelters from a concentrated model to a balanced one;(2) The spatial distribution of the shelters evolves from one that defies the characteristics of a fractal structure to one that completely fits the characteristics.
Key words:emergency shelter; grid dimension; evolution; Jianchuan city
Research on the Evolution of Emergency Shelters in Jianchuan City Based on Grid Dimension Method
DAO Ren, WANG Pei-ming, FANG Shuo, CHEN Xuan-xian
(School of Architecture and Urban Planning, Yunnan University, Yunnan Kunming 650504, China)
P315.9;TU976.56
A
10.13693/j.cnki.cn21-1573.2017.03.003
1674-8565(2017)03-0015-06
国家自然科学基金“基于分形理论的山地小城市避灾空间布局评价及优化研究——以地震灾害为例”(41361092)
2017-03-18
2017-06-27
刀认(1988- ),女,云南省勐腊县人,毕业于云南大学,硕士研究生,现主要从事城市防灾减灾及城市规划设计方面的研究。E-mail:893411210@qq.com
