基于双GNSS天线及单陀螺的车轮转角测量系统

缪存孝 楚焕鑫 孙志辉 徐纪洋 马 飞

(1.北京科技大学机械工程学院， 北京 100083； 2.上海联适导航技术有限公司， 上海 201702)

基于双GNSS天线及单陀螺的车轮转角测量系统

缪存孝1楚焕鑫1孙志辉1徐纪洋2马 飞2

(1.北京科技大学机械工程学院， 北京 100083； 2.上海联适导航技术有限公司， 上海 201702)

针对农业机械自动导航中，传统绝对角度传感器连接件多、安装复杂且容易出现故障，而陀螺测量前轮转角虽然安装容易，但陀螺零偏等仪器误差造成测量误差随时间累积的问题，提出了基于双GNSS天线和单轴MEMS陀螺组合测角系统，该系统通过双GNSS天线解算的航向角、速度等信息计算观测量，通过卡尔曼滤波器对陀螺计算的角度进行实时校正，提高了车轮转角的测量精度。实车试验结果表明，该系统具有较好的合理性和准确性，车轮转角测量结果与绝对角度传感器输出结果比较：直线试验误差在0.5°以内，曲线试验误差在1°以内，满足了农业机械自动导航的测角精度要求。

车轮转角； 双GNSS天线； 单轴MEMS陀螺； 卡尔曼滤波

引言

随着精准农业的快速发展，农业机械自动导航系统因其有利于减少农作物生产的投入成本，减少作业能耗等优点得到了越来越广泛的应用[1-3]。农业机械自动导航中车轮转角信息是影响导航效果的重要因素之一[4-5]。

目前农机自动导航采用的角度测量方法有2种：一种是采用电位移传感器、绝对编码器等绝对角度传感器测量车轮转向的绝对角度[6-7]；另一种是采用陀螺等惯性器件检测车轮的相对转动角度[8]，对安装在车轮转动部件上的陀螺输出的角速率信息处理后积分得到车轮的转动角度信息[9-11]。

绝对角度传感器虽然角度输出可以满足转角精度要求，但传感器连接件多，安装复杂，标定工作繁琐，并且容易出故障，检修和更换过程复杂，耗费大量时间和人力[12]。陀螺作为惯性器件，安装简便，工作寿命长[13]，但陀螺输出中包括零偏、随机漂移等误差项，造成误差随时间累积，测量精度下降[14]。文献[15]对陀螺数据用时间平滑模型建模后通过卡尔曼滤波来估计陀螺输出，减少了陀螺随机误差的影响，但该过程没有对常值误差进行处理，误差还是随时间累积。本文拟设计由双全球导航卫星系统(Global navigation satellite system，GNSS)天线和单轴微机电系统(Micro-electro-mechanical system，MEMS)陀螺组成的测角系统，通过双GNSS天线输出的速度、航向角等信息对车轮角度计算结果进行实时校正，提高角度测量精度，并安装在拖拉机上进行实车测试，验证算法的有效性。

1 系统设计

1.1 测角理论

如图1所示安装关系，系统主要包括2个GNSS天线组成的双天线导航系统和1个单轴MEMS陀螺。双GNSS系统的2个天线安装在车辆主体的两侧，基线垂直于车头与车尾的中轴线，双GNSS系统能够输出车体的运动速度、姿态角及经纬度等信息，能够完成自动驾驶系统需要的车辆姿态信息测量，同时为车轮转角校正提供信息；单轴MEMS陀螺安装在车轮转动部件上，敏感轴垂直于地面，测量车轮的转动速度。

图1 系统安装示意图Fig.1 Diagram of system installation1.车轮 2.单轴MEMS陀螺 3.GNSS天线1 4.GNSS天线2

单轴MEMS陀螺测量的车轮转动速率包括车体航向角的变化速率和车轮相对于主体的转动角速率，即

(1)

(2)

式中θ——车轮转角真值

由于陀螺输出中有零偏、随机漂移等误差项，所以实际应用中ωA还包含输出误差，造成角度积分的结果误差随时间累积。因此需要设计卡尔曼滤波器对误差进行实时校正。

角度计算值为

(3)

对式(3)求导得

(4)

式(4)中计算角速率等于陀螺测量真值加陀螺零偏减去航向角变化速率，即

(5)

根据式(5)与式(1)得角度计算的误差微分方程为

(6)

MEMS陀螺零偏为一阶马尔科夫过程，一阶马尔科夫过程微分方程表示为

(7)

根据车辆运动学模型[16]可知

(8)

则由双GNSS系统输出的车辆速度和航向角变化速率可以算出期望的车轮转角为

(9)

1.2 速度杆臂效应误差补偿

图2 GNSS天线杆臂示意图Fig.2 Diagram of lever-arm between GNSS and rear axle

主GNSS天线与后轮轴中心的杆臂长度为

式中φ——航向角γ——横滚角

车辆转动角速度矢量为

则杆臂效应造成的速度误差δv表示为

(10)

将GNSS天线测量的水平速度按照运动航向角方向分解到正东和正北2个方向，即

则经过杆臂误差补偿的速度为

(11)

1.3 卡尔曼滤波器设计

设计基于双GNSS天线及单陀螺的车轮转角测量系统，系统数据处理流程框图如图3所示。

图3 测角系统框架简图Fig.3 Algorithmic block diagram

陀螺数据与双GNSS天线航向角信息得到车轮转向角速度，积分后得到转向角度，双GNSS系统速度信息进行杆臂误差补偿后与航向角速率计算车轮转角理想值，将计算值与理想值作差作为量测值代入卡尔曼滤波器进行最优估计，卡尔曼滤波输出的角度误差和陀螺零偏对角度计算积分过程进行反馈校正，得到车轮转角的精确信息。

根据系统特点及数据处理过程，定义系统状态量为

式中δθk——k时刻的角度误差εk——k时刻的零偏

建立本系统的卡尔曼滤波状态方程[20]

Xk=Φk,k-1Xk-1+Wk

(12)

其中

(13)

式中Xk——k时刻的系统状态向量Φk,k-1——离散系统状态转移矩阵Wk——离散时间过程噪声，为N(0,Qk) 的高斯白噪声

Qk——系统噪声的方差矩阵，本文系统中为陀螺随机白噪声及零偏的激励白噪声

Δt——滤波时间间隔

F(tk-1)——连续时间状态转移矩阵

根据式(6)、(7)，计算得出

(14)

系统的观测量根据式(3)、(9)选取角度估计误差为

(15)

式中Zk——k时刻的系统观测向量

建立本系统的观测方程为

Zk=HkXk+Vk

(16)

其中

式中Hk——观测矩阵Vk——观测噪声，为N(0,Rk) 的高斯白噪声

Rk——系统噪声的方差矩阵，本系统中量测计算的误差白噪声

卡尔曼滤波算法可由下述方程描述：

一步预测方程

Xk,k-1=Φk,k-1Xk-1

(17)

状态递推方程

Xk=Xk,k-1+Kk(Zk-HkXk,k-1)

(18)

增益方程

Kk=Pk,k-1H′k(HkPk,k-1H′k+Rk)′

(19)

均方误差阵

Pk,k-1=Φk,k-1Pk-1Φ′k,k-1+Qk-1

(20)

Pk=(I-KkHk)Pk,k-1

(21)

式中Kk——k时刻的滤波器增益Pk——k时刻系统对象的状态估计误差协方差

I——单位矩阵

2 试验验证

2.1 试验平台

为检验本文所建系统的正确性，搭建了车轮转角测量系统的试验平台，如图4所示。

图4 测角系统试验平台Fig.4 Experiment platform1.MEMS陀螺仪 2.霍尔效应角度传感器 3.双GNSS天线

试验平台包括：黄海金马904-1型拖拉机1台、联适R60s系列双天线定位定向系统1套、日本SSS公司CRM 100型高精度单轴陀螺仪1只及相应数据处理电路、RTY050HVEAX型Honeywell霍尔效应绝对角度传感器1个、相应的数据传输线路及1台导航计算机。2个GNSS接收天线安装在车体两侧，基线距离为2.05 m，R60S系统输出航向精度优于0.05°，横滚角精度优于1°；MEMS陀螺和绝对角度传感器安装在车辆前轮的转向部件，测量同一侧转向轮的转角，各传感器与导航计算机之间通过相应数据线连接。

相应算法编写成DLL函数形式，编写软件从串口读取各个传感器信息并调用DLL函数完成前轮转动角度的计算，并将结果与绝对传感器输出角度保存。

试验中当车辆速度为零时，根据式(9)量测计算值分母为接近零的小值，计算结果无法反映当前车轮实际转角，所以在实际应用中需要进行速度判定：在车辆静止时车轮转角保持不变；当车辆开始运动时，陀螺数据积分并开始调用卡尔曼滤波过程，校正车轮的转角信息。系统中由于天线定位滞后等造成的延迟误差与系统测量精度量级相当，作为卡尔曼滤波器的观测噪声以消除对结果精度的影响。

2.2 试验结果与分析

在同一运动状态下，测量绝对角度传感器与MEMS陀螺测角系统输出的角度结果进行比较，验证本文提出的双GNSS天线及单轴MEMS陀螺车轮转角测量系统的正确性和有效性。

驾驶拖拉机在试验场地分别走一段直线路径和一段S曲线路径，在行驶过程中实时采集各传感器的数据和双GNSS天线及单轴MEMS陀螺组成的测角系统输出的车轮转角信息，以便分析和处理。

图5 直线试验路线Fig.5 Straight road test result

直线行驶路径如图5所示，整个过程人工驾驶，所以行驶路径不是严格的直线，前轮有转动。以起始点坐标为原点，利用经纬度计算各采集点与原点间的距离，画出直线行驶的路线图。图6为直线试验航向角度及航向角微分得到的航向角速率数据曲线。

直线试验数据处理过程中，卡尔曼滤波器的增益矩阵元素和估计误差协方差矩阵元素如图7所示，卡尔曼滤波器在一段时间后估计误差协方差与滤波增益收敛到稳定值，卡尔曼滤波器的状态估计收敛，说明所设计滤波器是稳定的。

图6 直线试验航向角度和角速率曲线Fig.6 Heading angle and angular rate of straight road

图7 直线试验卡尔曼滤波增益矩阵K元素和误差协方差阵P元素Fig.7 Gain matrix and error covariance matrix of Kalman filter

图8 直线行驶角度输出对比曲线Fig.8 Angle output contrast of straight road test

直线行驶时，绝对传感器输出角度、陀螺积分角度及经过滤波后的车轮转角角度输出结果如图8所示。陀螺积分初值取0°，由图8可知，陀螺积分直接计算角度误差随着时间累积，120 s试验时间内误差累积达到10°以上，这一误差会严重影响自动驾驶系统的导航精度，甚至造成系统失衡。而滤波角度在速度为零时保持初值不变，在车辆启动后，调用卡尔曼滤波过程经过双GNSS天线输出的航向角速率、速度等信息计算期望车轮转角对陀螺计算角度进行校正，滤波器收敛后系统的角度输出的误差不随时间累积，能够保证拖拉机自动驾驶的长时间稳定工作。为了分析卡尔曼滤波器对角度误差的补偿效果，表1列出了霍尔传感器、滤波前后角度在稳态情况下输出的部分数据，双GNSS系统及单陀螺组成的测角系统直线试验时输出结果与角度真值之间误差收敛后平均值为-0.064°，均方差为0.309°。本文设计的转角测量系统直线行驶时与霍尔效应角度传感器输出对比误差在0.5°以内，满足自动驾驶系统要求的车轮转角测量精度要求。

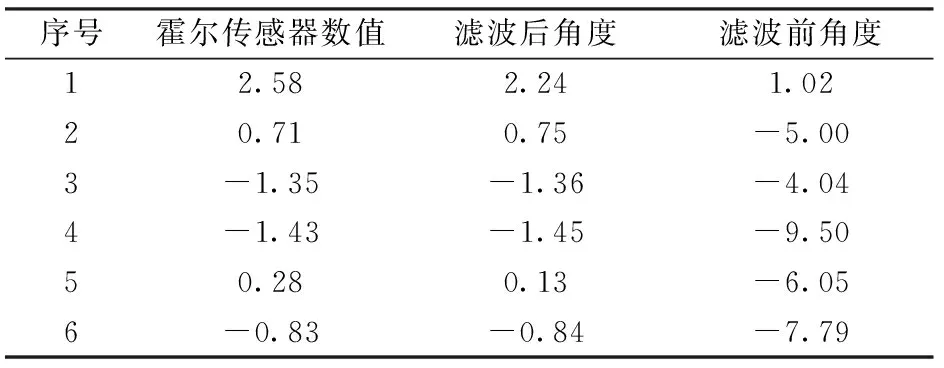
表1 霍尔传感器、滤波前后角度输出Tab.1 Hall effect sensor output, angle after and before Kalman filter (°)

图9 曲线试验路线Fig.9 Curve road test result

S曲线行驶路线如图9所示，车辆行驶路径为S曲线，通过补偿杆臂误差和不补偿杆臂误差角度输出对比，验证系统的精度。图10为S曲线试验航向角度及航向角微分得到的航向角速率数据曲线。

S曲线补偿杆臂试验数据处理过程中，卡尔曼滤波器的增益矩阵元素和估计误差协方差矩阵元素如图11所示，估计误差协方差与滤波增益收敛到稳定值，卡尔曼滤波器的状态估计收敛，说明所设计滤波器是稳定的。

图10 曲线试验航向角度和角速率曲线Fig.10 Heading angle and angular rate of curve road test

图11 曲线试验卡尔曼滤波增益矩阵K元素和误差协方差阵P元素Fig.11 Gain matrix and error covariance matrix of Kalman filter

S曲线行驶时，杆臂补偿前的角度输出结果及经过杆臂误差补偿的车轮转角角度输出结果与绝对角度传感器输出的对比如图12所示。结果表明，在大角度转弯未进行杆臂误差补偿时，双GNSS系统及单陀螺测角系统的角度输出在曲线行驶时误差较大，误差在曲线处达10°以上；经过杆臂误差补偿后，系统在曲线行驶时角度输出误差减小。为了分析杆臂补偿前后效果，表2列出了霍尔传感器、杆臂补偿前后角度输出的部分数据，通过杆臂补偿算法，系统在曲线试验时角度输出与霍尔效应传感器误差平均值为0.299°，均方差为1.009°。本文设计的转角测量系统曲线行驶时与霍尔效应角度传感器输出对比误差在1°以内，满足自动驾驶系统对车轮转角的测量精度要求。

图12 曲线行驶角度输出对比曲线Fig.12 Angle output contrast of curve running test

综上所述，本文提出的双GNSS系统及单陀螺组成的车轮转角测量系统能够代替传统绝对角度测量装置，并且能够解决陀螺测角由于零偏等器件误差引起的角度误差累积问题，同时，在曲线运动时通过补偿杆臂效应造成的速度误差提高了曲线运动时系统角度输出的精度，验证了本文提出系统的可行性和有效性。

表2 霍尔传感器、杆臂补偿前后角度输出Tab.2 Hall effect sensor output, angle after and before lever-arm compensation (°)

3 结束语

针对农机自动驾驶系统中车轮转角测量问题，设计了一种双GNSS系统及单轴MEMS陀螺组成的转角测量系统。从理论方面推导了陀螺测量车轮转角的可行性及误差来源，针对陀螺输出中零偏等误差项使角度输出误差随时间累积的问题，设计了相应的卡尔曼滤波器对角度测量进行最优估计，并对速度进行了杆臂效应补偿，提高观测量精度。安装在拖拉机上进行路面试验结果表明，本文提出的测角系统精度与霍尔角度传感器输出角度之间误差直线行驶时在0.5°左右，曲线行驶时在1°以内，满足自动驾驶系统的测量精度要求，验证了测角系统的可行性和有效性。

1 LI M, KENJI I, KATSUHIRO W, et al. Review of research on agricultural vehicle autonomous guidance[J]. International Journal and Biological Engineering, 2009,2(3):1-16.

2 林志海,白洪波. 浅谈GNSS卫星定位和自动驾驶系统在现代化农机具中的应用[J]. 农业机械, 2015(1):137-141.

3 崔冰. 简述农业机械化现状与发展趋势[J]. 现代农业, 2010(11):78-79.

4 ROVIRAMAS F. Sensor architecture and task classification for agricultural vehicles and environments[J]. Sensors, 2010, 10(12):11226-11247.

5 胡静涛,高雷,白晓平,等. 农业机械自动导航技术研究进展[J]. 农业工程学报, 2015, 31(10):1-10. HU Jingtao, GAO Lei, BAI Xiaoping, et al. Review of research on automatic guidance of agricultural vehicles[J]. Transactions of the CSAE, 2015, 31(10):1-10. (in Chinese)

6 SANTANA F, GOMEZ J. Design and implementation of a GPS guidance system for agricultural tractors using augmented reality technology[J].Sensors, 2010,10(11):10435-10447.

7 王鹤, 胡静涛, 高雷. 农业机械自动导航车轮转角测量误差补偿模型[J/OL]. 农业机械学报, 2014,45(8):33-37. http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?flag=1&file_no=20140806&journal_id=jcsam. DOI：10.6041/j.issn.1000-1298.2014.08.006. WANG He, HU Jingtao, GAO Lei. Compensation model for measurement error of wheel turning angle in agricultural vehicle guidance[J/OL]. Transactions of the Chinese Society for Agricultural Machinery, 2014,45(8):33-37. (in Chinese)

8 MEISER V, HESSELBARTH H, HENKE R, et al. Autonomous unmanned ground vehicle as sensor carrier for agricultural survey tasks[C]∥Proceedings International Conference of Agricultural Engineering,2014:Ref-CO266.

9 连志鹏. 自动驾驶农机转向控制研究[D]. 上海:上海工程技术大学, 2015.

10 陈艳,张漫,马文强，等. 基于GPS 和机器视觉的组合导航定位方法[J]. 农业工程学报, 2011,27(3): 126-130. CHEN Yan, ZHANG Man, MA Wenqiang, et al. Positioning method of integrated navigation based on GPS and machine vision[J].Transactions of the CSAE, 2011,27(3):126-130. (in Chinese)

11 周俊,姬长英. 自主车辆导航系统中的多传感器融合技术[J].农业机械学报, 2002,33(5): 113-116. ZHOU Jun, JI Changying. Multi-sensor fusion in navigation of autonomous vehicle[J]. Transactions of the Chinese Society for Agricultural Machinery, 2002, 33(5):113-116. (in Chinese)

12 贾全. 拖拉机自动导航系统关键技术研究[D]. 北京:中国农业机械化科学研究院,2015.

13 PAUL D. Navigation using inertial sensors[J]. IEEE Aerospace & Electronic System Magazine, 2015,2(2):42-69.

14 李军,马蓉. 拖拉机自动转向系统设计研究[J]. 拖拉机与农用运输车, 2012, 39(5):51-54,58. LI Jun, MA Rong. Design and study of tractor automatic steering system[J]. Tractor & Farm Transporter, 2012, 39(5):51-54,58. (in Chinese)

15 王朝阳. 基于陀螺仪的车辆前轮转角测量方法研究[D]. 上海:上海工程技术大学,2015.

16 李逃昌,胡静涛,高雷,等. 基于模糊自适应纯追踪模型的农业机械路径跟踪方法[J/OL].农业机械学报,2013,44(1):205-210. http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?flag=1&file_no=20130139&journal_id=jcsam. DOI：10.6041/j.issn.1000-1298.2013.01.039. LI Taochang, HU Jingtao, GAO Lei, et al. Agricultural machine path tracking method based on fuzzy adaptive pure pursuit model[J/OL]. Transactions of the Chinese Society for Agricultural Machinery,2013,44(1):205-210. (in Chinese)

17 于海业,马成林,孙瑞东. 角速度计检测信号数字滤波处理的研究[J]. 农业机械学报, 1997,38(4):86-89. YU Haiye, MA Chenglin, SUN Ruidong. A study on signals detected by angle velocity meter digital filter processing[J]. Transactions of the Chinese Society for Agricultural Machinery, 1997,38(4):86-89. (in Chinese)

18 严恭敏,严卫生,徐德民. 捷联惯性测量组件中内杆臂效应分析与补偿[J]. 中国惯性技术学报，2008，16(2): 148-153. YAN G M，YAN W S，XU D M． Analysis and compensation on inner lever arm effect of strapdown inertial measurement unit[J]. Journal of Chinese Inertial Technology, 2008,16(2): 148-153. (in Chinese)

19 高伟,张亚,孙骞，等. 传递对准中杆臂效应的误差分析与补偿[J]. 仪器仪表学报,2013,34(3):560-565. GAO Wei, ZHANG Ya, SUN Qian, et al. Error analysis and compensation for lever-arm effect in transfer alignment[J]. Chinese Journal of Scientific Instrument,2013,34(3):560-565. (in Chinese)

20 周建军,王秀,张睿,等. 农机车载GPS和DR组合导航系统定位方法[J/OL]. 农业机械学报, 2012, 43(增刊):262-265. http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?flag=1&file_no=2012s54&journal_id=jcsam. DOI：10.6041/j.issn.1000-1298.2012.S0.054. ZHOU Jianjun, WANG Xiu, ZHANG Rui, et al. GPS/DR integrated navigation positioning method for agricultural machinery[J/OL]. Transactions of the Chinese Society for Agricultural Machinery,2012,43(Supp.):262-265. (in Chinese)

WheelTurningAngleMeasurementSystemBasedonDoubleGNSSAntennasandSingleGyro

MIAO Cunxiao1CHU Huanxin1SUN Zhihui1XU Jiyang2MA Fei2

(1.SchoolofMechanicalEngineering,UniversityofScienceandTechnologyBeijing,Beijing100083,China2.ShanghaiAllyNavTechnologyCo.,Ltd.,Shanghai201702,China)

For the problem that the traditional angle sensor’s complex mechanical structure and prone to failure and the gyro bias cause the error accumulates over time in automatic driving system, a wheel turning angle measurement system based on double GNSS antennas and single gyro was proposed. The system’s sensors mainly included two GNSS antennas and a MEMS gyro. The double GNSS antennas were mounted on both side of the vehicle and provided the speed, attitude angle, latitude and longitude of the vehicle. The single MEMS gyro was mounted on the wheel and the angular rate was measured. An algorithm used the above data was designed to integrate the angular rate to obtain the steering angle. In order to solve the problem that the error accumulates over time, a Kalman filter based on the vehicle dynamics model was designed to calibrate the error of integration of the gyro data. At the same time, the lever-arm compensation algorithm was used to solve the speed error caused by lever-arm. The straight line experiment was carried out to verify the effectiveness of the system and the curve line experiment was carried out to verify the effectiveness of the lever-arm compensation algorithm. Compared the steering angle of the proposed system with the Hall effect angular sensor, the average error of the straight line experiment was -0.064° and the error variance was 0.309° and the cure line experiment’s mean error was 0.299° and the error variance was 1.009°. The result of the experiments showed that this system could replace the traditional angle sensor and it was easy to install and overhaul.

wheel turning angle; double GNSS antennas; uniaxial MEMS gyro; Kalman filter

S24; TP271

A

1000-1298(2017)09-0017-07

10.6041/j.issn.1000-1298.2017.09.002

2017-03-24

2017-07-03

国家自然科学基金项目(61603035)

缪存孝(1981—)，男，讲师，博士，主要从事惯性器件应用研究，E-mail: miao_cunxiao@163.com