电力系统暂态时域仿真的区间改进欧拉法

钱莉

摘要电力系统暂态时域仿真中，一些参数在测量和实际运行中存在不确定性，故引入区间改进欧拉法进行暂态时域仿真。本文将传统暂态仿真中的数据转化为区间数处理，将某些参数设置为区间数，利用改进欧拉法交替求解DAE问题，得出参数变化对系统相对功角的影响。结合IEEE-39算例进行区间改进欧拉法的暂态时域仿真，分析表明本文方法是有效的。

关键词电力系统；暂态时域仿真；区间运算；改进欧拉法；交替求解

随着社会的发展，现代电网规模和复杂度越来越大，维持电力系统的暂态稳定非常重要，对电力系统进行暂态稳定计算分析是至关重要的。系统暂态稳定分析目前应用最广泛的是时域仿真法，可适用于大型电力系统，时域仿真法中常用的是改进欧拉法和隐式梯形积分法。在参数测量及实际运行时，电力系统的各项数值存在着不确定情况，故利用区间方法来对电力系统进行暂态时域仿真能较好地囊括这些不确定情况。本文所用的改进欧拉法来交替求解DAE问题时，可消除“交接误差”，花费机时少。因而，本文提出一种利用区间改进欧拉算法来实现电力系统暂态时域仿真的方法，计及系统中参数发生微小变化，得出微小变化对于相对功角产生的影响。

1基于改进欧拉法的暂态时域仿真区间算法

1.1区间数的定义

犹如有理数可以看作一对有序整数，复数可以看成一对有序实数一样，也可以定义区间数如下：

1.2电力系统暂态时域仿真的改进欧拉法

暂态仿真中系统的数学模型一般形式可表示为

1.3暂态时域仿真的区间改进欧拉法

基于上述改进欧拉法的暂态时域仿真，在进行区间运算时，必须将所有变量转化为区间数处理。本文将发电机的机械功率作为区间数来处理，通过编程实现电力系统暂态时域仿真，得到发电机相对功角随时间的变化图，得出发电机的机械功率对功角变化的影响。

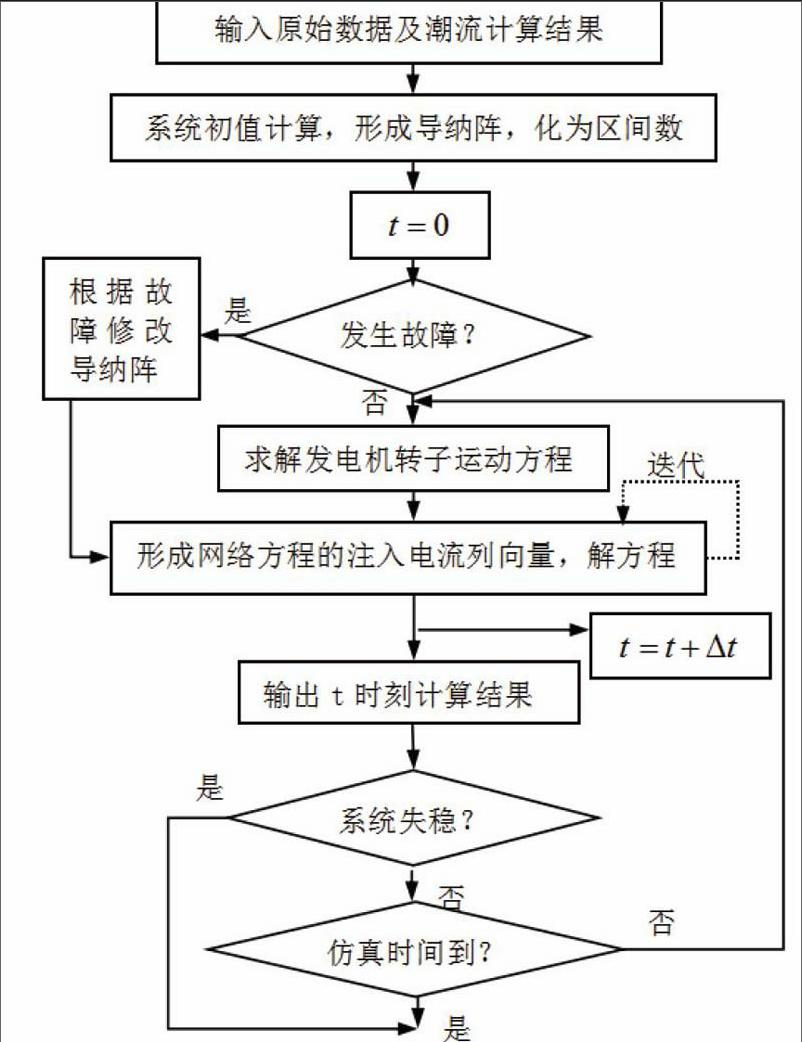
本文利用改进欧拉法对式（3）交替求解，对电力系统进行区间暂态仿真。在区间改进欧拉法的计算中，需要通过迭代消除交接误差对于式（3），在交替求解时，求得t时刻的状态量后，可由此计算tk+1时刻的状态量。

2算法实现

本文利用matlab软件编写了电力系统暂态时域仿真的区间改进欧拉法程序。首先是将实数转化为区间数计算，然后制定一些基本运算的算法，最后将其应用于改进欧拉法的暂态时域仿真中。以下2个方面是区间改进欧拉法暂态时域仿真的注意点：1）由于三角函数是非线性函数，在定义它的区间运算时要注意包含两个极值。2）在求解网络方程时，会涉及复区间数，为了简便求解，可将一组网络方程转化为xy同步坐标下的两组方程，此时方程中只含实数，转化为区间数后容易计算。若使用复区间数进行计算时，计算较为复杂，且会出现保守性过大的问题。

3算例分析

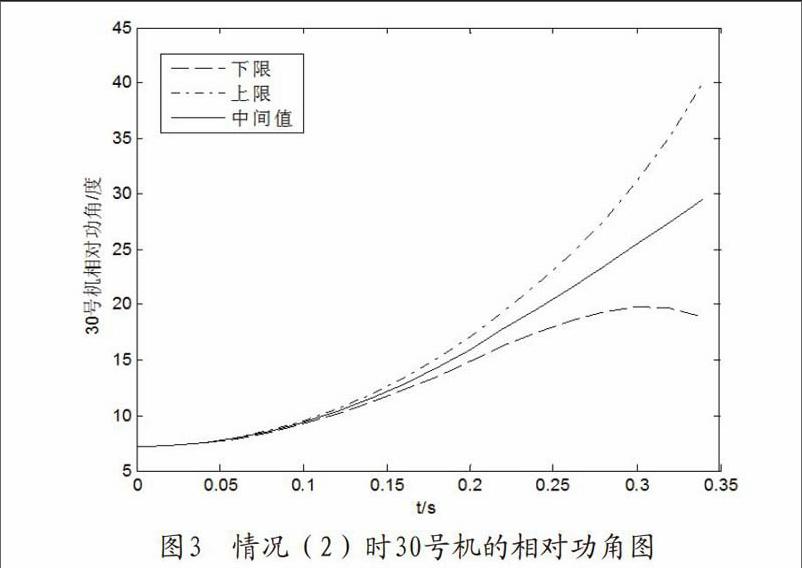
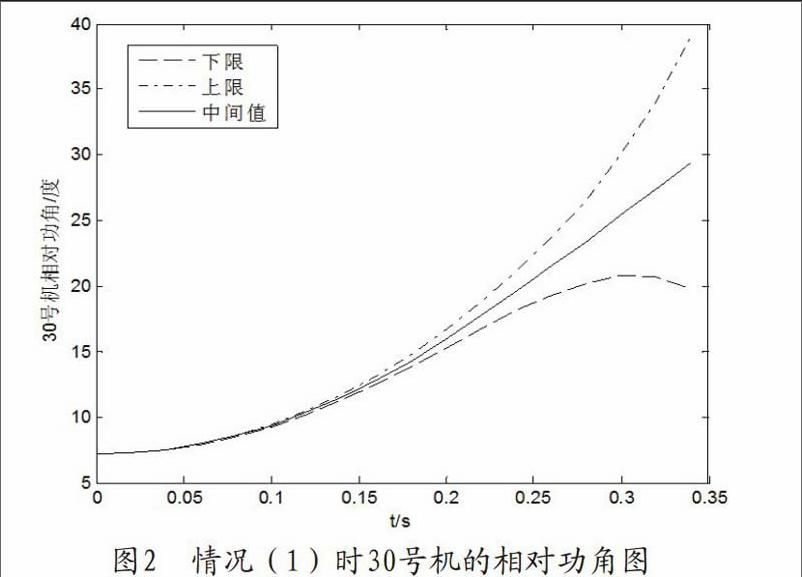
本文对于IEEE 39系统采用区间改进欧拉法进行暂态时域仿真，文中故障设置为0时刻线路4-14上节点4侧出口发生三相短路，0.2s（即10周波）切除故障，仿真步长为0.02s，在普通运算中（不设置为区间数），这一情况是暂态稳定的。下面针对机械功率设置了几种不同的情况，然后利用区间运算得出暂态仿真的相对功角变化图。1）将所有输入发电机的机械功率设置为区间数[0.98P，1.02Pj]，其他数据不作变动。2）将输入30号发电机的机械功率设置为区间数[0.95Pm，1.05Pm]，其他数据不作变动。

对上述情况分析可知：单台机的机械功率发生微小变化对其他发电机的影响很小。区间改进欧拉法相较于蒙特卡羅法可以大大节省时间，且有效的给出时域仿真的功角变化范围。但区间会产生累计效应，故本方法只适用于短时间的暂态计算。在实际情况中，机械功率都只是与测量值有微小变化，所以文中设置的参数区间值是有效且符合实际的。

4结论

本文基于区间理论及暂态仿真理论，提出了一种利用区间改进欧拉算法来实现电力系统暂态时域仿真的方法。该方法能够对于不确定性问题仿真出包含系统所有解的区间，简单易行，效果好。但是，该方法只适应于短时间的暂态计算，长时间计算保守性较大。所以区间改进欧拉法适用于系统参数发生小幅变化的短时间暂态时域仿真。endprint