SchWarzschild时空的边界条件与暗能量

胡锦文

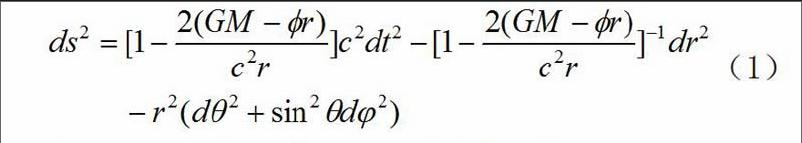
摘要在忽略宇宙因子的Schwarzschild时空中，规定满足无穷远欧几里得边界条件的真空引力势恒为0是不必要的，若假设这种真空引力是可以随着宇宙时间的演化而改变的，那么可以发现在Schwarzschild时空中远离星球的运动会产生一种斥力效应，它的斥力项与暗能量宇宙学常数模型中的斥力项具有相同的形式，这种假设也同时使得引力场方程存在了演化方向，而它可能与热力学时间箭头存在关联。

关键词Schwarzschild时空；真空引力势；斥力；暗能量；宇宙学常数为了从理论上说明这一点，人们提出了各种各样的模型，这些模型大都是基于标准模型进行改进，比如精质暗能量模型、幽灵暗能量模型、精灵暗能量模型等，它们共同的特点是在宇宙组分中引入一种新的、具有负压强的、在大尺度结构中均匀分布的动力学成分。其中最简单的这种模型是宇宙学常数模型，其特征是态函数为一个常数。

但是宇宙学常数模型存在了“宇宙巧合”问题，还有一个问题是按照真空量子场论的计算，会发现真空能密度与观测值相差了121个数量级，这即是“精细调节”问题。另一类理论解释则认为有必要对现今的引力理论进行修正，例如（R）引力理论，膜世界引力理论等，这些理论不需要引入暗能量，而是直接对时空曲率的修正来实现当前宇宙的加速膨胀，虽然取得了一定的成功，但也存在各自的局限性，例如目前还无法解决（R）引力理论的稳定性问题。

与上述两种常见方法不同的是，本文试图讨论Schwarzschild时空的边界条件，以此推导出了满足宇宙加速膨胀的边界。

1Schwarzschild时空的边界条件

在Schwarzschild时空中，通常的观念认为，当远离物质足够远时时空的标势x趋于牛顿引力势，并随着距离越大越逐渐趋于真空的引力势为0。这种边界条件显然不是满足无穷远欧几里得条件的唯一边界条件，而更一般的边界条件是：远离物质无穷远的真空引力势为0，0是空间均匀的，但是可能会随着宇宙的时间演化而改变，因而應当有0=0（f）。下面基于这种边界条件来讨论Schwarzschild时空的性质。

在上述的边界条件下Schwarzschild时空的外部度规（忽略宇宙因子A）为：

处在上述度规场中的在，处观察者测得的自由落体的加速度为

2讨论

从上述的分析可知，如果假设无穷远处满足欧几里得条件的真空的时空边界条件不是引力势恒为0，而是可能会随着宇宙时间的演化而改变，并且当这种改变随时间为增时（即0，>0），那么对处于Schwarzschild时空中的远离星球运动的物质，会产生一种斥力效应，并且随着两者的距离越大，这种斥力效应相对于引力效应越明显。以及与暗能量宇宙学常数模型中的斥力效应进行比较，发现它们的斥力项具有相同的形式，都与距离呈正比。

但是与宇宙学常数模型不同的是，采用了该边界条件的Schwarzschild时空，当物质向着星球运动时，由式（8）可见，V1<0时表明引力效应被增强。除此之外，并未表明0必须为一常量，这意味着它在宇宙的不同时期可能起着不同的作用。

0不恒为0意味着引力场方程的演化存在一个方向，而从式（9）看出，这个方向与宇宙空间膨胀的方向具有各自独立性，那么，这两个独立的时间箭头会与热力学时间箭头存在关联吗？这将在下一篇文章中给出讨论。endprint