玻璃纤维筋在地铁围护桩设计中的研究及应用

冯红喜， 杨旭升

(黄河勘测规划设计有限公司， 河南 郑州 450003)

玻璃纤维筋在地铁围护桩设计中的研究及应用

冯红喜， 杨旭升

(黄河勘测规划设计有限公司， 河南 郑州 450003)

为解决当前地铁建设中玻璃纤维筋在盾构端头围护桩中大量应用而相应圆形截面玻璃纤维筋混凝土构件设计计算等研究不足这一矛盾，通过公式推导得到基于混凝土受压破坏的圆形玻璃纤维筋混凝土受弯构件的正截面承载力计算公式，并与现有行业标准《盾构可切削混凝土配筋技术规程》中关于圆形玻璃纤维筋混凝土受弯构件正截面承载力计算公式进行对比，从配筋及安全储备等角度进行分析。结果表明： 相比《盾构可切削混凝土配筋技术规程》中关于玻璃纤维筋圆形混凝土构件正截面承载力的计算公式，本文所推导基于混凝土受压的玻璃纤维筋混凝土圆形截面构件计算公式在直径不大于1 m、设计承载弯矩小于1 000 kN·m 时，配筋量设计更为优化，有利于控制造价，进一步研究发现当直径大于1 m时，本文所推导公式在减少配筋、控制造价上更有优势。

玻璃纤维筋； 玻璃纤维筋混凝土构件； 地铁； 圆形截面； 围护桩； 截面承载力

Abstract: The glass fiber reinforced plastics (GFRP) have been widely used in retaining pile of end soil of shield metro; but the study of the bearing capacity of circular cross-section of GFRP reinforced concrete components is insufficient. As a result, the calculation formula of the cross-section bearing capacity of the rounded GFRP reinforced concrete flexural components based on concrete compressive failure is deduced. And then it is compared with the calculation formula of the existing industry standard,TechnicalSpecificationforShield-cuttableConcreteReinforcement, in terms of the reinforced bar and safety reservation. The results show that, compared to the existing industry standard, the calculation formula deduced is superior to that from the existing industry standard in terms of reinforced bar design and construction cost under the conditions of diameter of component less than 1 m and design bearing capacity less than 1 000 kN·m; and after further study, the calculation formula deduced shows much more advantageous in terms of reinforced bar control and construction cost under the condition of diameter of component larger than 1 m.

Keywords: glass fiber reinforced plastics (GFRP); GFRP reinforced concrete component; metro; circular cross-section; retaining pile; cross-section bearing capacity

0 引言

玻璃纤维筋(以下简称GFRP筋)是由玻璃纤维和树脂等材料固化而成的筋材，作为一种新型材料，其密度小、弹性模量低[1]、耐腐蚀性好、具备良好的电磁绝缘性，同时抗剪强度低，有良好的切割性能[2]。在当前城市轨道交通大发展背景下，GFRP筋正成为解决地铁建设中盾构端头钢筋混凝土围护结构与盾构连续掘进这一矛盾的关键因素。

目前国外对GFRP筋混凝土构件已进行了较多的研究。文献[3-4]试验发现受力作用下普通钢筋混凝土梁变形小于纤维筋(以下简称FRP筋)混凝土梁的变形，同时总结了FRP筋梁的变形特性； Bradberry[5]认为GFRP筋混凝土构件应按超筋设计，以确保混凝土破坏模式为受压破坏； Choi等[6]通过试验发现GFRP筋与混凝土的黏结强度低于普通钢筋。国内针对GFRP筋混凝土构件的研究起步相对较晚，但也取得了较大的发展。高丹盈等[7-8]对玻璃纤维聚合物筋的类型和配筋率对裂缝及梁挠度的影响进行了研究； 张志强等[9]推导了GFRP 筋混凝土梁受弯承载力、界限受压区高度的计算公式，并用试验数据进行了验证； 葛文杰等[10]提出了FRP 筋和钢筋混合配筋增强混凝土梁2种名义配筋率和3种破坏模式的概念； 徐岱等[11-12]根据相关设计规范提出同时配有钢筋和GFRP筋的圆截面混凝土受弯构件的承载力设计计算方法； 刘军等[1,13]结合北京地铁16号线研究了GFRP筋在盾构工程中的应用。

以上研究成果多集中在GFRP混凝土梁与普通钢筋混凝土梁受力及变形特性等理论方面，应用于指导实际工程还有待进一步深入，同时研究大多针对矩形截面梁，对于当前实际工程中采用较多的盾构围护桩这一圆形截面混凝土构件研究有限。鉴于此，本文以呼和浩特市地铁2号线某站为例，对现有规范CJJ/T 192—2012《盾构可切削混凝土配筋技术规程》(以下简称《规程》)关于圆形截面GFRP筋混凝土受弯构件的正截面承载力计算公式进行简化，方便实际工程应用； 同时推导得到基于混凝土受压破坏圆形截面GFRP筋混凝土受弯构件的正截面承载力计算公式，并与《规程》相关内容进行对比，分析两者在配筋计算方面的差别，为地铁围护桩结构设计提供参考。

1 GFRP筋混凝土的设计原理

1.1 GFRP筋混凝土破坏模式

混凝土破坏共有3种模式： 平衡破坏、受拉破坏和受压破坏。由于GFRP筋没有明显的塑性屈服阶段，如按照平衡破坏模式进行设计，GFRP筋混凝土构件极易呈现为脆性破坏； 若按照受拉破坏进行设计，由于受压区混凝土未达应变极限，其参数都难以确认，且也为脆性破坏。综上，应考虑混凝土受压时在GFRP筋混凝土构件完全破坏前，受压区混凝土会经历一定的塑性变形，混凝土从开裂到最后破坏会有一个裂缝逐渐增大的过程，具有一定的破坏预兆。

1.2 基本假定

为简化计算，借鉴普通钢筋混凝土构件受弯特性，特作如下基本假定：

1)截面应变应保持平面，即截面内任意点的混凝土应变和GFRP筋应变与该点到中和轴的距离成正比；

2)不计混凝土的抗拉强度；

3)不计GFRP筋的抗压强度；

4)混凝土和GFRP筋存在良好的黏结性能，其中混凝土的应力-应变关系满足线性混凝土设计规范，如图1所示；

图1 混凝土应力-应变曲线

5)GFRP筋的应力-应变关系满足线性关系，GFRP筋拉应力不大于其设计极限强度。

2 GFRP筋混凝土构件圆形截面承载力计算

地铁设计中对圆形截面GFRP筋混凝土构件受弯承载力计算，传统分析主要分为2种： 1)不考虑GFRP筋的材料特性，直接等量替代普通钢筋，该种计算方式常见于采用理正等软件直接进行配筋的计算中； 2)基于GFRP筋混凝土结构平衡破坏模式。由前文对GFRP筋混凝土破坏模式分析可知，以上计算方法均有不足。鉴于此，本文对比研究了基于混凝土受压破坏状态下圆形截面GFRP筋混凝土构件的2种计算方法： 1)《规程》提出的计算公式； 2)本文推导的基于受压破坏状态下圆形截面GFRP筋混凝土构件的计算公式。此外，本文也给出了GFRP筋混凝土构件斜截面承载力计算公式。

2.1 正截面受弯承载力计算

2.1.1 《规程》关于圆形截面GFRP筋混凝土构件正截面受弯承载力计算

《规程》参考《混凝土结构设计规范》沿周边均匀配置纵向普通钢筋的圆形截面混凝土偏心受压构件正截面受弯承载力计算公式，同时考虑弯矩调整系数K，得到圆形截面周边均匀配置GFRP筋混凝土构件正截面受弯承载力，能够保证混凝土构件为受压破坏。混凝土构件正截面受弯承载力如图2所示。

图2 《规程》周边均匀配置GFRP筋圆形截面混凝土构件正截面受弯承载力图

Fig. 2 Sketch of flexural bearing capacity of circular cross-section concrete with uniform configuration of GFRP from relevant technical specification

(1)

(2)

式(1)—(2)中：Af为纵向受拉GFRP筋的截面面积；fc为混凝土轴心抗压强度设计值；ffu为GFRP筋抗拉强度设计值；α1为变异系数；A为圆形混凝土构件截面面积；r为圆形截面半径；rs为纵向GFRP筋重心所在圆周的半径；α为对应于受压区混凝土截面面积圆心角与2π比值；αt为纵向受拉GFRP筋与全部GFRP筋截面面积比值，αt=1.25-2α，α≥0.625时αt=0；K为设计弯矩调整系数，取1.4；M为构件正截面所受变矩。

鉴于以上计算公式多涉及超越方程，不便于在实际设计中使用，现考虑采用曲线拟合对以上公式进行如下简化：

令式(1)变换为ffuAf=ηAfc，

(3)

其中

(4)

令式(2)变换为M=λAfcrs，

曲线拟合≈3.171 3α2-0.661 2α+0.044 9。

(5)

式(2)也可转换为M=ψAfffurs，

曲线拟合≈-2.216 5α2-0.160 9α+0.875。

(6)

φ1 000 mm GFRP筋围护桩在不同弯矩作用下的配筋计算结果如表1所示。

表1φ1 000 mm GFRP筋围护桩在不同弯矩作用下的配筋计算结果

Table 1 Reinforced bar calculation results ofφ1 000 mm GFRP retaining pile under different bending moments

弯矩/(kN·m)《规程》配筋值Af/mm2简化公式配筋值A′f/mm2Af-A′fAf/%800952995120．189001115711165-0．07100012977129540．18110014929148970．2112001695717012-0．32130019436193200．60

比较发现，简化公式值和《规程》值误差在0.6%以内，从而验证了本简化公式的准确性，同时简化公式可以避免求解繁杂超越方程，方便实际工程应用。

2.1.2 受压破坏状态下圆形截面GFRP筋混凝土构件正截面承载力的公式推导

基于GFRP筋在圆形截面受力过程中始终处于线弹性阶段，未达到抗拉强度设计值，同时与中和轴距离差异的GFRP筋应力也各不相同的特点，如图3所示，通过求解GFRP筋带厚度，进而通过积分分别求出弓形混凝土受压区面积质心到中和轴的距离和GFRP筋带合力及其对中和轴的力矩，得到如下公式：

A1r2α1fc+C1εcuEfρfr2=0；

(7)

Mu≤B1r3α1fc+D1εcuEfρfr3。

(8)

其中：

A1=πα-sin πα·cos πα；

(9)

(10)

(11)

(12)

(13)

式(7)—(13)中：fc为混凝土轴心抗压强度设计值；ffu为GFRP筋的抗拉强度设计值；ρf为截面纵向GFRP筋的配筋率；Ef为GFRP筋的弹性模量；α为对应于受压区混凝土截面面积圆心角与2π比值，(-α，α)范围内为有效混凝土受压区；θ0为对应于实际受压区混凝土截面面积的圆心角与2π比值；θ0=arccos(1-2ξ)，(-πθ0，πθ0)范围内不考虑GFRP筋作用；ξ=x0/2r，x0为截面实际受压区高度；εcu为正截面混凝土极限压应变；Mu为正截面受弯承载力设计值；β为混凝土等效矩形应力图中受压区高度xc与平截面假定所确定的实际受压区高度x0的比值。

图3基于受压破坏的周边均匀配置GFRP筋圆形截面混凝土构件正截面受弯承载力图

Fig. 3 Flexural bearing capacity of circular cross-section concrete component by uniform configuration of GFRP under compressive failure

2.1.3 2种计算方法的对比分析

2.1.3.1 计算结果的对比

根据以上2种GFRP筋混凝土构件受弯承载力计算公式，现给出φ1 000 mm圆形截面的GFRP筋混凝土构件在不同弯矩作用下的配筋结果，如表2和图4所示。

表2φ1 000 mm圆形截面GFRP筋混凝土构件配筋对比

Table 2 Comparison between calculation formula deduced and existing calculation formula in terms of reinforced bar of GFRP reinforced concrete components ofφ1 000 mm circular cross-section

弯矩/(kN·m)《规程》计算配筋量/mm2安全系数推导公式计算配筋量/mm2安全系数8009529900111571000129771100149291200169571300194361．468298839111861397717167209671．35～1．52

注： 安全系数指混凝土构件处于极限状态时弯矩与构件设计弯矩之比，文献[14]指出安全系数在(1.07，2.21)范围内均属合理范围。

图4 φ1 000 mm圆形截面GFRP筋混凝土构件配筋对比图

Fig. 4 Comparison between calculation formula deduced and existing calculation formula in terms of reinforced bar of GFRP reinforced concrete components ofφ1 000 mm circular cross-section

通过以上分析可以得到：

1)本文所推导的基于GFRP筋混凝土受压破坏计算公式，所得配筋量与《规程》计算配筋量比值由小到大，其主要原因是基于GFRP筋混凝土构件混凝土受压破坏推导的公式认为GFRP筋在受力过程中，未达到设计强度，且每根筋应力均不相同。同时，随着弯矩增加，GFRP筋发挥的应力越来越少。

2)直径1 m的混凝土构件，在弯矩小于1 200 kN·m时，从配筋量看可以发现《规程》设计略显保守；在大于1 200 kN·m时两者配筋量相差不大。

3)进一步分析其他桩径在不同弯矩作用下的配筋计算结果可得，桩径大于1 m时，同桩径同弯矩的条件下本文推导的公式计算配筋量均小于《规程》计算配筋量，即随着桩径的增大，在保证安全系数的基础上本文推导的计算公式更有利于降低工程造价。

2.1.3.2 计算原理的对比

1)关于圆形截面GFRP筋混凝土构件正截面承载力计算，《规程》是参考《混凝土结构设计规范》圆形截面混凝土偏心受压构件正截面受弯承载力，通过施加弯矩调整系数K所得到的，却未能考虑受压破坏中GFRP筋处于弹性阶段，未达到极限应变这一重要特征； 本文推导的公式则充分考虑了GFRP筋在受力过程中未达极限应变的特点。

2)《规程》中关键的参数K值建立在大量钢筋和GFRP筋圆梁承载力试验比值的统计数据基础之上，借鉴了美国ACI规范中关于实际配筋率与平衡配筋率比值为1.4时混凝土受压破坏有可靠保证的规定，而实际上GFRP筋与普通钢筋的受力模式和材料特性均有所不同； 本文推导公式的各项参数则物理意义明确。

2.2 斜截面受剪承载力计算

GFRP筋混凝土构件抗剪承载力VU主要由混凝土抗剪承载力Vc和GFRP筋抗剪承载力Vf组成，即

VU=Vc+Vf。

(14)

针对混凝土抗剪承载力，我国主要借鉴美国ACI规范相关规定，其无腹筋混凝土抗剪承载力

(15)

其中

(16)

针对圆形截面的GFRP筋抗剪承载力Vf，国内研究相对较少，考虑斜裂缝与GFRP筋夹角为45°和GFRP筋在达到极限承载力时遭到破坏，文献[15]和《盾构直接切割围护结构始发与接收技术规程》均提出了圆形截面的GFRP筋抗剪承载力计算公式

(17)

其中

ffv=min(0.004Ef，ffb)；

(18)

ffb=(0.05rb/d+0.3)fgu≤fgu。

(19)

式(17)—(19)中：Afv1为单肢GFRP箍筋截面面积；S为纵向箍筋间距；ffv为GFRP箍筋抗剪强度设计值；ffb为GFRP筋弯曲段抗拉强度设计值；rb为GFRP筋弯曲半径；d为GFRP筋名义直径；fgu为GFRP筋极限抗拉强度设计值。

文献[15]通过试验得到GFRP筋构件抗剪承载力并与以上理论值进行对比，误差在2%，验证了以上公式的可行性和准确性。

3 工程案例

3.1 工程概况

本车站为呼和浩特市2号线1期工程某一标准站，为单柱双层车站，采用“围护桩+内支撑”的围护结构。标准段围护桩为φ800@1 200，盾构段围护桩采用φ1 000@1 400，其中在盾构门洞范围内，考虑盾构掘进便捷，提高工程效益，降低施工风险，采用GFRP筋桩为φ1 000@1 400。

3.2 计算结果及配筋

利用理正深基坑7.0求解得到GFRP筋桩的内力包络图如图5所示，然后采用如上计算方式得到配筋结果如图6所示。

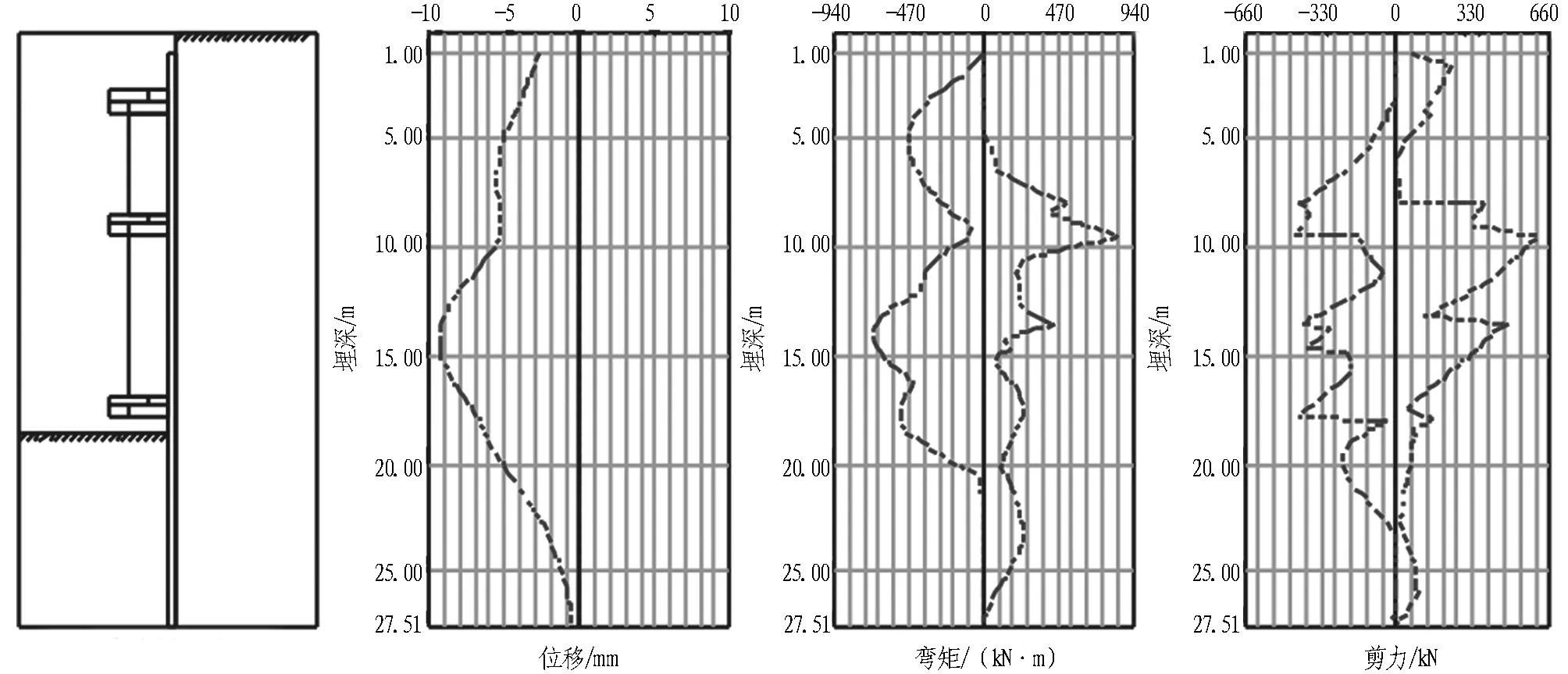
(a) 支撑竖向布置图 (b) 位移(-9.41～0 mm) (c) 弯矩(-686.91～851.18 kN·m) (d) 剪力(-442.13～598.41 kN)

图5φ1 000 mm GFRP筋桩内力包络图

Fig. 5 Envelope diagram of internal force ofφ1 000 mm GFRP pile

图6 φ1 000 mm GFRP筋桩配筋图

根据以上计算结果，分别得到《规程》计算配筋量和本文推导公式计算的配筋量，如表3所示。

表3φ1 000 mm GFRP筋桩配筋对比

Table 3 Comparison between calculation formula deduced and existing calculation formula in terms of reinforced bar ofφ1 000 mm GFRP pile

《规程》配筋值Af/mm2推导公式值A′f/mm2钢筋节省率/%10356783924．31

由表2和表3分析可知，在满足安全储备要求的基础上，本文推导公式较《规程》配筋量节省了24.31%。

4 结论与讨论

1)依据φ1 000 mm围护桩在不同弯矩作用下的配筋计算表明，由《规程》中圆形截面GFRP筋混凝土构件正截面承载力计算公式所得到的计算简化公式，与原公式误差控制在0.6%以内，验证了简化公式的准确性，方便了实际工程中的设计应用。

2)对比本文推导公式和《规程》给出的公式所得配筋设计，对圆形截面直径不大于1 m、设计承载弯矩小于1 000 kN·m的GFRP筋混凝土构件，从配筋量上可以反映出《规程》设计略显保守； 进一步研究发现，随着圆形截面直径增大，当直径大于1 m时，在保证安全系数的基础上本文推导的计算公式更有利于降低工程造价。

3)从计算原理来看，《规程》未能考虑GFRP筋材料特性及受力模式等因素，在同样满足安全储备的前提下，本文所推导公式的理论基础更为合理，物理参数更为明确。

4)在当前GFRP筋大量应用于地下工程尤其是地铁建设的大背景下，针对GFRP筋围护桩的布筋方式在采用混合配筋或非均匀配筋等方面有待进一步地研究。

[1] 刘军，原海军，李京凡，等. 玻璃纤维筋在盾构工程中的研究与应用[J]. 都市快轨交通， 2014， 27(1)： 81. LIU Jun，YUAN Haijun，LI Jingfan，et al. Current state of research and application of GFRP in shield engineering[J]. Urban Rapid Rail Transit， 2014， 27(1)： 81.

[2] 逄显昱，李颖娜，赵欣，等.玻璃纤维筋围护桩设计与施工的应用研究[J]. 铁道标准设计， 2015， 59(10)： 108. PANG Xianyu，LI Yingna，ZHAO Xin，et al. Design and construction of glass fiber reinforced supporting pile and its application[J]. Railway Standard Design，2015，59(10)： 108.

[3] EDWARD G N，GARY E N，CHARES J P． Behavior of fiber glass reinforced concrete beams[J]．Journal of the Structural Division， 1971， 97(9): 2203．

[4] EDWARD G N，GARY E N． Fiber glass reinforced concrete slabs and beams[J]．Journal of the Structural Division，1977， 103(2): 421．

[5] BRADBERRY T E．FRP-bar-reinforced concrete bridge decks[J]．Transportation Research Board Proceedings， 2001: 94．

[6] CHOI Dong-uk, CHUN Sung-chul. HA Sang-su. Bond strength of glass fibre-reinforced polymer bars in unconfined concrete[J]．Engineering Structures， 2012(34): 303．

[7] 高丹盈，赵军，BRAHIM B． 玻璃纤维聚合物筋混凝土梁裂缝和挠度的特点及计算方法[J]．水利学报，2001，(8): 53． GAO Danying， ZHAO Jun， BRAHIM B. The characteristics of crack and deflection and its calculating method of concrete beam reinforced with glass fiber polymer bars[J]. Journal of Hydraulic Engineering， 2001(8): 53.

[8] 高丹盈，BRAHIM B. 玻璃纤维聚合物筋混凝土梁正截面承载力的计算方法[J].水利学报， 2001(9): 73． GAO Danying， BRAHIM B．Calculation method of flexural capacity of GFRP-reinforced concrete beam[J]. Journal of Hydraulic Englineering， 2001(9): 73.

[9] 张志强，师晓权，李志业 . GFRP 筋混凝土梁正截面受弯性能试验研究[J].西南交通大学学报，2011，46(5): 745. ZHANG Zhiqiang， SHI Xiaoquan，LI Zhiye. Experimental investigation of flexural behavior of concrete beams strengthened with GFRP[J]. Journal of Southwest Jiatong University， 2011， 46(5)： 745.

[10] 葛文杰，张继文，戴航，等.FRP筋和钢筋混合配筋增强混凝土梁受弯性能[J].东南大学学报(自然科学版)，2012， 42(1): 114. GE Wenjie， ZHANG Jiwen， DAI Hang，et al. Flexural behavior of concrete beam with hybrid reinforcement of FRP bars and steel bars[J]. Journal of Southeast University(Natural Science Edition)， 2012， 42(1): 114.

[11] 徐岱，樊有维，陶铸. 混合配置GFRP筋与钢筋的圆形截面混凝土受弯构件承载力计算[J]. 混凝土与水泥制品， 2015(3): 43. XU Dai，FAN Youwei，TAO Zhu. Flexural capacity calculation of circular cross-section concrete members with hybrid reinforcement of GFRP bars and rebars[J]. China Concrete and Cement Prodoucts， 2015(3): 43.

[12] 徐岱. GFRP筋混凝土圆截面构件抗弯性能研究[D].南京： 南京林业大学， 2014. XU Dai. Study of flexural behavior of concrete beam of circular section reinforced with GFRP bars[D].Nanjng： Nanjing Forestry University， 2014.

[13] 金鑫，刘军，周洪，等. 玻璃纤维筋在地铁盾构始发中的应用[J].北京建筑大学学报， 2016， 32(1): 52. JIN Xin， LIU Jun， ZHOU Hong， et al. Application of GFRP Bars in the subway shield-driven[J]. Journal of Beijing University of Civil Engineering and Architecture， 2016， 32(1): 52.

[14] 冯鹏，叶列平，黄羽立，等. 受弯构件的变形性与新的性能指标的研究[J].工程力学， 2005， 22(6): 28. FENG Peng，YE Lieping，HUANG Yuli，et al. Deformability and new performance indices of flexural members[J]. Engineering Mechanics， 2005， 22(6): 28.

[15] 刘军，王芳，周洪，等. 圆形截面玻璃纤维筋混凝土桩体抗剪承载力研究[J].土木工程学报，2016，49(9): 103. LIU Jun，WANG Fang，ZHOU Hong，et al. Study of shear strength of glass fiber-reinforced polymer(GFRP) rebar concrete piles with circular cross-sections[J]. China Civil Engineering Journal， 2016， 49(9): 103.

StudyandApplicationofGlassFiberReinforcedPlastics(GFRP)toDesignofMetroRetainingPile

FENG Hongxi, YANG Xusheng

(YellowRiverEngineeringConsultingCo.,Ltd.,Zhengzhou450003,Henan,China)

U 45

A

1672-741X(2017)09-1134-06

2016-10-24;

2017-03-02

冯红喜(1986—)，男，河南南阳人，2015年毕业于北京交通大学，隧道及地下工程专业，硕士，助理工程师，现主要从事轨道交通结构设计工作。E-mail： fhxjiaotong@163.com。

10.3973/j.issn.1672-741X.2017.09.011