考虑电杆影响的架空配电线路雷电感应电压计算

张天忠 陈 伟 谈 超 肖冬萍 梅道珺

(1. 安徽省电力公司， 合肥 230061； 2. 安徽华电工程咨询设计有限公司， 合肥 230022；3. 重庆大学输配电装备及系统安全与新技术国家重点实验室， 重庆 400044)

考虑电杆影响的架空配电线路雷电感应电压计算

张天忠1陈 伟2谈 超2肖冬萍3梅道珺3

(1. 安徽省电力公司， 合肥 230061； 2. 安徽华电工程咨询设计有限公司， 合肥 230022；3. 重庆大学输配电装备及系统安全与新技术国家重点实验室， 重庆 400044)

线路绝缘闪络的预防需考虑杆塔对雷电电磁场和感应电压的影响。在考虑杆塔和有耗大地影响的情况下，采用FDTD法计算雷电电磁场，并结合场线耦合Agrawal模型对架空线路感应雷过电压进行计算，利用二维计算解决三维结构问题。结果表明：该方法能有效反映场域内多种介质对雷电电磁场和场线耦合效应的影响；杆塔顶部雷电电场畸变并显著增强，感应电压形成尖峰，而线路其他位置的感应电压也稍大于只考虑有耗大地影响的计算结果。

雷电感应电压； 架空配电线路； 杆塔； 绝缘

雷击大地时，雷电释放出的脉冲电流将在数千米的空间范围内产生强烈的辐射电磁场。架空输配电线路距离长，裸露于空气当中，极易与雷电电磁场相耦合，形成线路过电压，严重的会造成线路对地或相间闪络、损坏端接变压器及开关设备等。对于 35 kV及以下的架空配电线路而言，由于绝缘水平较低，雷电感应过电压已成为线路雷害跳闸增多的主要原因[1-2]。正确评估架空电力线路雷电感应过电压的强度和时变特性，对于线路防雷、确保其安全稳定运行具有重要意义。

随着雷电感应的危害逐渐为人们所认识，国内外学者对架空电力线路感应雷过电压已开展了一些实测和仿真研究。雷电感应过电压理论计算分两步：雷电电磁场计算和场线耦合计算。其中，对于雷电电磁场计算先后提出了偶极子法[3]、Wait法[4]、Cooray-Rubinstein近似公式法[5]、时域有限差分法(FDTD)[6-8]等方法；对于场线耦合提出了Taylor[9]、Agrawal[10]和Rashidi 3种等效模型。已有文献讨论了雷电流波形、回击模型、土壤特性等因素对线路感应雷过电压的影响。

研究中为了能够更加准确地评估悬挂于杆塔处的绝缘子所承受的雷电感应电压，特别提出考虑杆塔对雷电电磁场时间、空间传播特性和架空线路感应电压的影响。鉴于FDTD法能够较好地反映瞬态电磁场和电磁耦合效应的时变特性，尤其是能反映场域空间不同介质的作用，因此，在考虑杆塔和有耗大地影响的情况下，采用FDTD法计算雷电电磁场，并将场线耦合Agrawal模型和FDTD法相结合对架空线路雷电感应电压进行数值计算。

1 理论方法和计算模型

1.1基于FDTD的雷电电磁场计算

雷电流激励所产生的空间电磁场具有轴对称性，因此可在二维柱坐标系内进行计算。图1所示为二维柱坐标系Yee网格单元中3个场分量的位置。

(1)

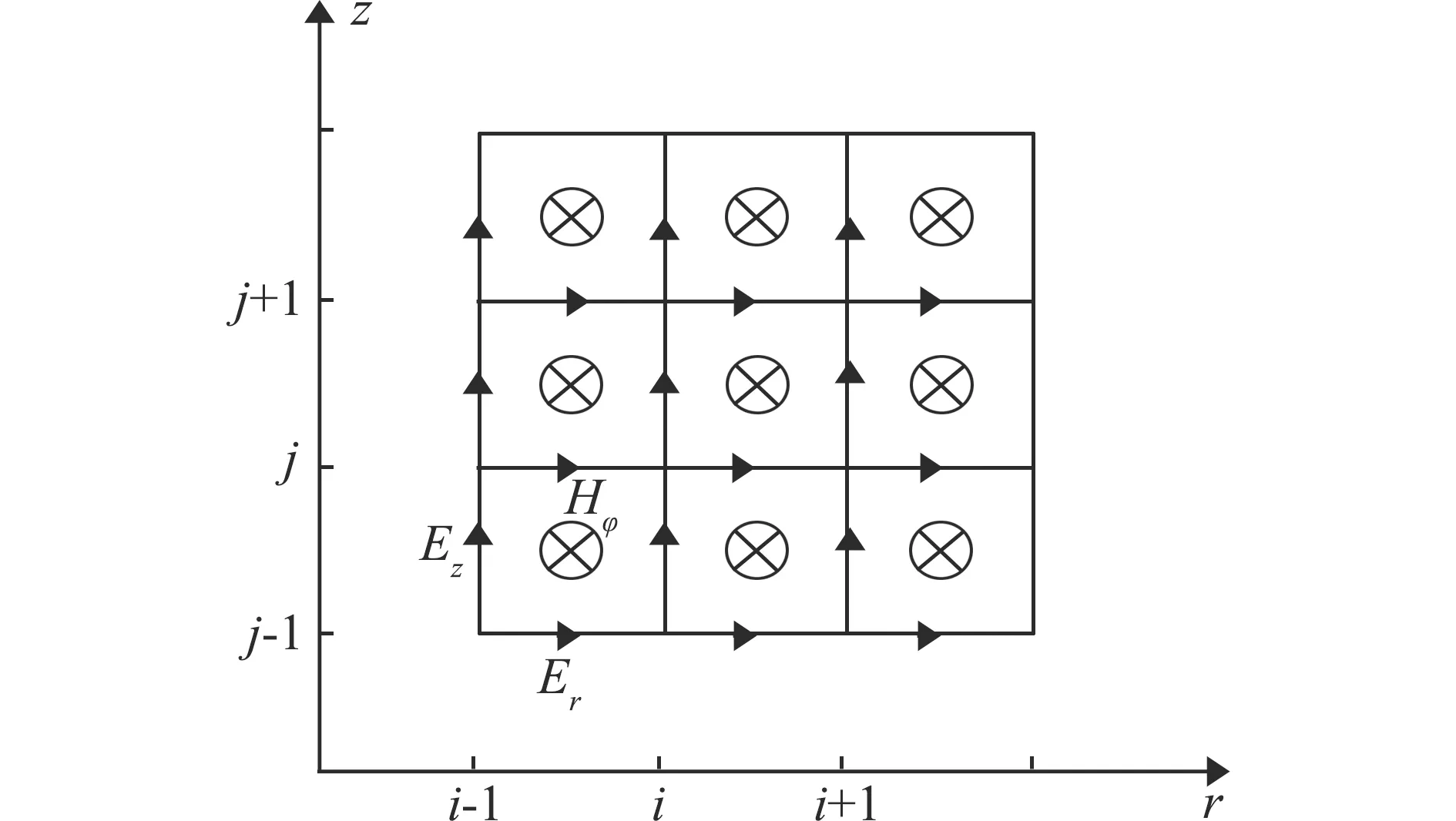
图1 雷电电磁场FDTD计算单元

(2)

(3)

式中： Δr——r方向上的网格尺寸；

Δz——z方向上的网格尺寸；

Δt—— 时间步；i——r方向上的网格数；

j——z方向上的网格数；

n—— 迭代时间步数；

ε、μ和σ—— 雷电电磁场传播空间介质的介电常数、磁导率和电导率。

对于大地与空气、杆塔与空气的交界面，介电常数、磁导率和电导率可取2种介质参数的平均值。

雷电流回击通道上的Ez需要做特殊处理，根据安培环路定律可得其计算式

(4)

截取有限的场域空间进行FDTD计算，采用一阶Mur吸收边界条件。

1.2架空电力线路雷电感应电压计算

雷电电磁场对多导均匀无损架空电力线路的耦合通常采用Agrawal模型进行等效，其等效电路如图2所示。

图2 雷电电磁场与多导架空线路耦合的Agrawal模型

按照FDTD算法思想对传输线方程组进行网格离散可得

(5)

(6)

在线路首位两个端部应满足边界条件[12]

(7)

(8)

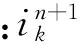
L和C—— 多导传输线系统单位长度电感矩阵和电容矩阵；

ZS和ZL—— 线路始端和终端端接阻抗向量；

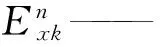
线路上的雷电感应电压为散射电压与入射电压之和

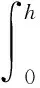
(9)

1.3架空电力线路与雷击通道三维结构的处理

通常情况下，架空电力线路与雷击通道的空间位置是如图3所示的三维结构。

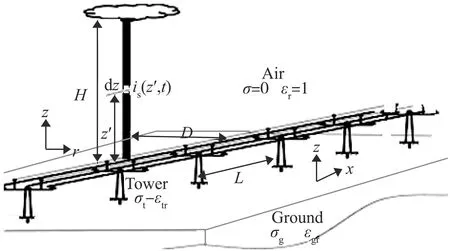
图3 架空电力线路与雷击通道的三维空间结构

为了避免复杂而繁琐的三维雷电电磁场计算，提高计算效率，可将二维柱坐标系内计算的Er分量进行分解转换，获得沿导线轴向(即x方向)的分量Ex。转换时所使用的坐标设置如图4所示。

图4 Er转换为Ex的坐标图

转换关系式满足

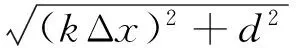
(10)

2 算例分析

2.1雷电流模型及线路结构设置

为了较准确地描述雷电通道基底电流脉冲前沿陡峭、达到峰值后平稳衰减的特征，研究采用双Heidler函数对其进行建模：

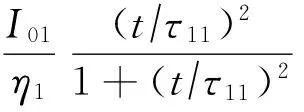
(11)

式中：I01、I02—— 用于限定电流峰值；

η1、η2—— 峰值电流修正系数；

τ11、τ21—— 用于限定波头时间；

τ12、τ22—— 用于限定波尾时间。

带入表1所列参数，模拟1.2/50 μs雷电流，峰值为30 kA。

表1 基底雷电流波形参数

回击电流采用MTLE模型，其数学形式为：

i(z′,t)=e-λz′is(0,t-z′vi)t≥z′vi

(12)

式中：z′ —— 雷电通道高度；

λ—— 衰减常数；

vi—— 回击电流传播速度。

三相架空线路截面结构如图5所示，相导线等效半径9 mm，端接匹配阻抗。

图5 三相架空线路截面结构

设土壤的相对介电常数为12，电导率为0.1 S/m。对于配电线路，杆塔为混凝土杆，设其相对介电常数为10，电导率为0.001 S/m，杆塔档距100 m。

(1) 算例1：为了更加直观地显示杆塔对雷电电磁场空间传播及线路雷电感应电压的影响，先设置如图6所示的雷击点与线路空间位置，其中雷击点距离最近一基杆塔的距离为200 m。三相导线结构如图5所示。

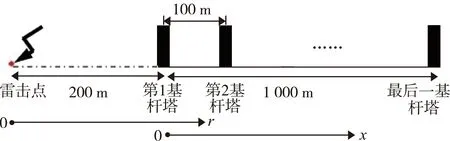
图6 雷击点与线路结构(算例1)

图7a、b所示分别为雷击后5 μs时近地局部空间雷电电磁场分布和三相架空线路沿线感应电压分布曲线。靠近雷电通道的区域电磁场非常强，但是为了在一个比较宽的区域内显示雷电电磁场空间分布，设置了色图所能显示的电场和磁场阈值，计算结果高于阈值时以阈值对应的颜色显示。图8为沿相线的雷电感应电压分布曲线。

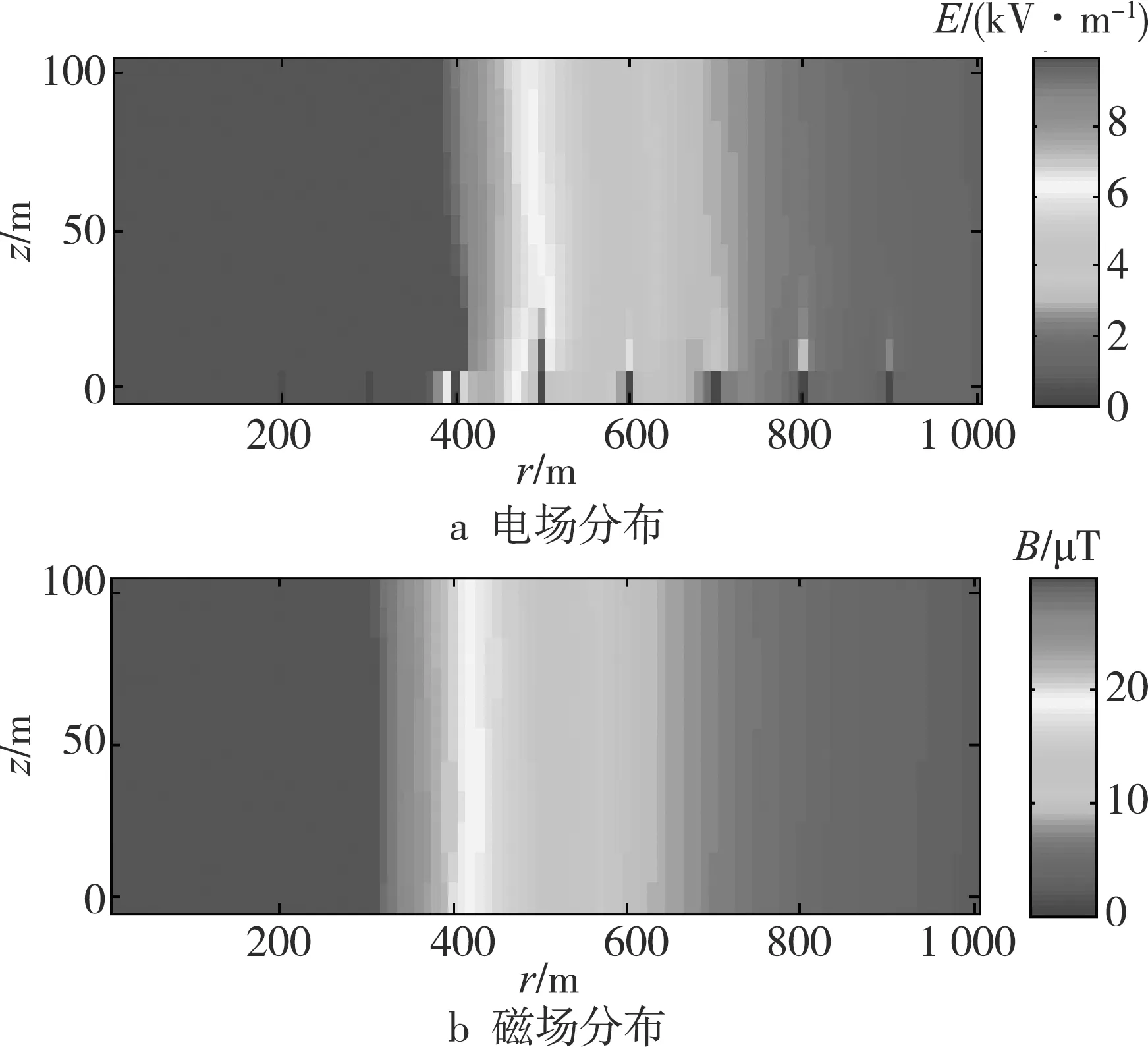
图7 雷电电磁场空间分布

由图7和8可看出，在雷电电磁场的空间发展过程中，杆塔位置的电场畸变，并且其顶部场强增强。由此，杆塔处线路上的雷电感应电压出现明显的尖峰，这一情况应该在线路防雷和绝缘设计时引起重视。

图8 沿相导线的雷电感应电压分布曲线

线上位置距离雷击点越远，则感应电压越小。由于三相导线呈对称结构，A、C相(即边相)上的感应电压大小和变化特征相同；而B相(即中相)位置稍高，对地电容较之A、C相小，则感应电压也稍高。这与雷电感应规程估算式所给出的规律是一致的，证明了本次研究提出的算法是有效的。

此外，对比3种模型参数设置情况下的计算结果，情况1：不考虑杆塔且取理想大地；情况2：不考虑杆塔且取有耗大地；情况3：考虑杆塔且取有耗大地。图9a、b所示分别为图6第2基杆塔所在位置处、第2、3基杆塔之间中间位置处线路感应电压的时域波形。

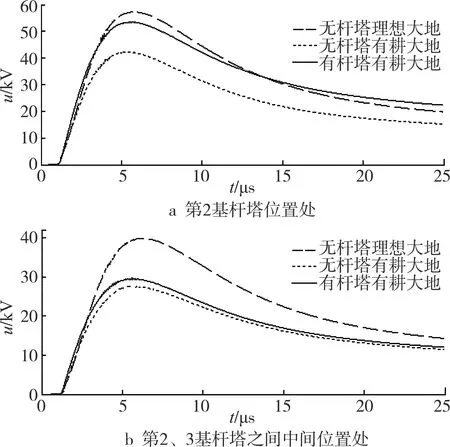
图9 不同介质情况下线路雷电感应电压时域波形

由图9a可看出，由情况1计算所得的线路感应电压幅值比较大；由情况2计算所得的线路感应电压幅值较小。上述结果在已有文献中已证实，并推荐在计算模型中考虑有耗大地的影响[13]。需注意的是，当加入杆塔后，杆塔端部位置电场局部显著增大，导致此处线路上的雷电感应电压也比较大。

由图9b可以看出，由情况1计算所得的线路感应电压幅值最大，由情况2计算所得的电压幅值最小。这是因为在计算模型中加入杆塔，杆塔之间空间内的雷电电场相比于不考虑杆塔时有所增大，但是增大幅度远不如杆塔端部。

(2) 算例2：设雷击点与配电线路的空间位置如图10所示，其中雷击点距离线路的垂直距离为50 m，距离最近的左侧第1基杆塔的水平距离为30 m。

图10 雷击点与线路结构(算例2)

图11a所示为邻近雷击点的左、右两侧第1基杆塔处边相和中相导线上的雷电感应电压时域波形。图11b所示为第4基杆塔边相上的雷电感应电压时域波形。

图11 不同杆塔位置线路雷电感应电压时域波形

从图11可看出，线路雷电感应电压与雷电流具有相似的时变特性，即较陡的上升沿，缓慢的下降沿。由于雷击点相对而言靠近左侧杆塔，因此在左侧线路上产生的雷电感应电压比右侧的高，线路中相的感应电压比边相高。随着与雷击点距离的增大，线路雷电感应电压减小，且具有一定的时间延迟。

3 结 语

(1) 此次研究提出的方法能够较准确地反映雷电电磁场和架空线路雷电感应电压的时间、空间传播特性，反映场域空间中多种介质对电磁场和场线耦合效应的影响。

(2) 杆塔顶部雷电电场畸变并且增强。沿整条线路来看，杆塔处线路的雷电感应电压形成明显的尖峰，增大了绝缘闪络的可能性。

(3) 相比于只考虑有耗大地影响的情况，加入杆塔后，线路雷电感应电压明显增大。

在杆塔影响下，绝缘子将承受较大的雷电感应电压。若对此预估不足导致选型不合理，发生绝缘子闪络的可能性将增大。此次研究可为架空电力线路的防雷和绝缘设计提供理论参考。

[1] CHISHOLM W A, CRESS S L, POLAKJ. Lightning-caused Distribution Outages[C]. Transmission and Distribution Conference and Exposition, 2001 IEEEPES, 28 Oct～2 Nov, 2001, 2:2502-2515.

[2] 文武.感应雷电磁干扰及防护研究[D].武汉:武汉大学,2004:10-12.

[3] RUBINSTEIN M, UMAN M A. Methodsfor Calculatingthe Electromagnetic Fields From a Known Source Distribution: Application to Lightning. IEEE Trans.on EMC, 1989, 31:183-189.

[4] MASTERM J, UMANM A. Transient Electric and Magnetic Fields Associated With Establishing a Finite Electrostatic Dipole[J]. IEEE Trans. on EMC, 1991, 33(4): 118-126.

[5] WAIT J R.On the Theory of Transient Electromagnetic Sounding Over a Stratifiedearth[J].Canadian Journal of Physics, 1972，50：1055-1061.

[6] CALIGARIS C, DELFINO F, PROCOPIO R. Cooray-Rubinstein Formula for the Evaluation of Lightning Radial Electric Fields: Derivation and Implementation in the Time Domain[J]. IEEE Trans. EMC, 2008, 50(1): 194-197.

[7] BERENGER J P. Long Range Propagation of Lightning Pulses Using the FDTD Method[J].IEEE Transactions on EMC，2005，47(4)：1008-1011.

[8] YANG C，ZHOU B.Calculation Methods of Electromagnetic Fields Very Close Tolightning[J].IEEE Transactions on EMC,2004，46(1)：133-141.

[9] TAYLOR C D, SCATTERWHITER S, HARRISONC W.The Response of a Terminated Two-wire Transmission Line Excited by a Nonuniform Electromagnetic Field[J].IEEE Trans. Antennas Propag，1965，13(6)：987-989.

[10] AGRAWAL AK.Transient Response of Multiconductor Transmission Line Excited by a Nonuniform Electromagnetic Field.IEEE Trans. EMC，1980, 22(2)：119-129.

[11] REN H M，ZHOU B H，VLADIMIR A R ,et al.Analysis of Lightning-induced Voltages on Overhead Lines Using a 2-D FDTD Methodand Agrawal Coupling Model[J].IEEE Transactions on EMC,2008，50(3)：651-659.

[12] 高方平.架空线感应雷过电压的计算与分析[D].杭州：浙江大学，2012:16-18.

[13] 翟绍思.配网架空线雷电感应过电压计算及闪络概率研究[D].北京：华北电力大学，2011:19-20.

Abstract:The influence of tower to lightning electromagnetic field(L-EMF) and lightning-induced voltage should be considered in the prevention of insulation flashover. Considering the effects of transmission-poles and the lossysoil, FDTD method is used to calculate L-EMF, which combines the field-line coupling Agrawal model to calculate the lightning-induced overvoltage of overhead lines. In addition, 3D structural problem is solved by two-dimensional computation. The results show that the proposed method can effectively reflect the influence of various media on the lightning electromagnetic field and the field-line coupling effect. The lightning electric field on the top of tower is distorted and obviously enhances, which consequently leads to the peak value of induced voltage. The lightning-induced voltage at other locations of the line is slightly larger than the calculation results with consideration of impact about lossy soil.

Keywords:lightning-induced voltage; overhead power lines; towers; insulation

CalculationofLightning-InducedVoltagesonOverheadDistributionLinesConsideringtheEffectsofTransmission-Poles

ZHANG Tianzhong1CHEN Wei2TAN Chao2XIAO Dongping3MEI Daojun3

(1.State Grid Anhui Electric Power Company, Hefei 230061, China;2.Anhui Huadian Engineering Consultating & Design Co., Ltd., Hefei 230022, China;3.State Key Laboratory of Power Transmission Equipment & System Security and New Technology, Chongqing University, Chongqing 400044, China)

TM153；TM726

A

1673-1980(2017)05-0088-06

2017-05-12

中央高校基本科研业务费项目“电力电缆接头状态非接触式检测原理及方法研究”(CDJXY150008)

张天忠(1968 — )，男，高级工程师，研究方向为电网建设。