混合WPD和ACPSO的负荷预测模型
2017-10-09匡卫洪董朕
匡卫洪, 董朕
(1.广州市电力工程设计院有限公司,广东 广州 510220,2.广东工业大学 自动化学院,广东 广州 510006)
混合WPD和ACPSO的负荷预测模型
匡卫洪1, 董朕2
(1.广州市电力工程设计院有限公司,广东 广州 510220,2.广东工业大学 自动化学院,广东 广州 510006)
为了解决传统BP神经网络对负荷高频分量预测精度不高、泛化能力弱的缺点以及粒子群算法(PSO)在解决高维、多模复杂问题时容易陷入局部最优的问题,提出了一种混合小波包变换和自适应交叉粒子群算法(ACPSO)优化神经网络的短期负荷预测新方法。通过小波包变换对负荷样本进行多层序列分解,对单支重构所得的负荷子序列采用自适应交叉粒子群算法优化的神经网络进行预测。最后叠加各子序列的预测值,得出实际预测结果。通过实际电网负荷预测表明,新模型能充分掌握负荷波动的变化规律,有效提高负荷波动大的地区的预测精度,且预测模型具有较强泛化能力。
小波包分解;自适应交叉粒子群算法;高频分量;神经网络;负荷预测
Abstract: To overcome low accuracy and weak generalization of forecasting of load high-frequency component through traditional BP neural network as well as local optimum which will probably occur when PSO is used to solve high-dimensional and multi-mode complex problems, this paper presents a new method for short-term load forecasting of the optimal neural network combining wavelet packet transform and adaptive crisscross particle swarm optimization (ACPSO). Wavelet packet decomposition(WPD)is used for multiple layer series decomposition of load sample, ACPSO is used to forecast the load sub-sequence obtained through single-branch reconstruction. Finally, forecast values of all sub-sequences are added to get actual forecasting result. Forecasting of actual grid load shows that the new model has quite strong generalization ability, and can grasp the regulation of load fluctuation and improve forecasting accuracy in areas of large load fluctuation.
Keywords: wavelet packet decomposition (WPD); adaptive crisscross particle swarm optimization (ACPSO); high-frequency component; neural network; load forecasting
0 引 言
电力系统负荷预测是电力系统规划的重要组成部分,其预测精度将会直接影响到电力系统运行的安全性、经济性和供电可靠性[1-2]。由于负荷本身的波动性和复杂性,以及人们对于电力需求也越来越大,还没有一种方法能够很好地解决预测中所面临的问题。其中,BP神经网络[3]由于网络结构、算法相对简单,可以实现从输入到输出的任意非线性映射,在负荷预测领域逐步得到了广泛应用。然而,因为BP神经网络采用梯度下降法来调整权值和阈值,所以导致算法收敛速度慢,容易陷入局部最优。此外,为了提高预测精度,更多的影响因素和学习样本将被考虑在内,神经网络的计算量、权值数以及阈值数都将急剧增加。
随着对短期负荷预测精度要求越来越高,各种改进的神经网络广泛应用于负荷预测中。文献[4]使用PSO优化BP神经网络进行预测,虽然收敛速度快,但当考虑因素增多,变量规模将会快速增大,PSO在求解大规模优化问题时容易出现‘维数灾’;文献[5]利用小波分解将负荷投影到不同尺度上进行预测,得到较高的预测精度,但分解后的高频分量复杂度较高,BP神经网络对其预测精度不高,所以该方法不适用于负荷波动大的地区;文献[6]等则将模糊系统与神经网络结合,取得较高的预测精度。
自适应交叉粒子群优化算法(adaptive crisscross particle swarm optimization,ACPSO)具有收敛速度快、全局性强的特点,解决了已有优化算法的不足。为了进一步提高预测精度,提出一种混合小波包分解(wavelet packet decomposition,WPD)与自适应交叉粒子群算法优化神经网络的负荷预测模型(WPD-ACPSO -NN),并对广东某实际电网进行了提前24 h预测。仿真结果表明,新方法有效提高负荷波动大的地区的预测精度。
1 自适应交叉粒子群算法(ACPSO)
为了解决粒子群算法[7]在解决高维、多模复杂问题时容易陷入局部最优的问题,提出一种自适应交叉粒子群算法。由于PSO在算法后期种群多样性减少,算法会出现早熟收敛问题。故提出一种自适应判定准则,并通过一种交叉算子来保证种群多样性,提高算法的全局收敛能力。ACPSO主要由二部分组成,分别为粒子群算子和交叉算子。
1.1 粒子群算子
PSO以种群中粒子作为优化目标的一个解,通过计算每个解的适应度值来选取全局最优粒子,依据最优粒子的位置来确定其它粒子的飞行方向和距离,依此来更新全部粒子的位子进行寻优。粒子更新迭代过程中产生个体极值和全局极值,个体极值是个体寻优过程中的最优解,全局极值则是全部粒子寻优过程中的最优解。其更新公式如下:
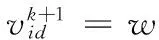
(1)
(2)
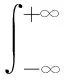
式中r1、r2为[0,1]之间的均匀分布随机数;c1、c2为加速因子;w为惯性权重;v是粒子的飞行速度(vmin 1.2.1自适应早熟判定准则 PSO算法中,粒子的位置决定了粒子适应度值,如果两个粒子的位置相同,那么它们的适应度值也应该一样。故通过种群中粒子适应度值的整体变化可以判定种群的状态。 设种群的大小为M,fm为粒子m的适应度值,favg为种群的平均适应度值,s2为种群的适应度值方差,s2可定义为: (3) 式中f为归一化定标因子,由下式计算: (4) 随着算法迭代次数的增加,不同粒子的适应度会越来越接近,因此s2会越来越小。s2越小,则群体中粒子的聚集程度越大,群体趋近于收敛。当s2小于某一个给定的阈值λ时,认算法进入后期搜索阶段,容易出现早熟收敛情况。当s2<λ时,本文通过引入交叉算子避免早熟现象出现。 1.2.2交叉算子 受儒家的中庸思想和遗传算法的交叉变异操作启发,引入一种交叉算子,即在PSO后期阶段有两个不同粒子进行交叉产生一个新的折中解来更新种群,交叉前需对全部粒子进行随机配对。假设2个粒子分别为X(i,d)和X(j,d),交叉操作如下: MShc(i,d)=r1*X(i,d)+(1-r1)*X(j,d)+ (5) MShc(j,d)=r2*X(j,d)+(1-r2)*X(i,d)+ (6) i,j∈N(1,M),d∈N(1,D) (7) 式中r1、r2为[0,1]之间的均匀分布随机数;c1、c2为[-1,1]之间的均匀分布扩展系数;MShc(i,d)、MShc(j,d)(d=1, 2…,D)为别为交叉后产生的折中解,即为X(i,d)和X(j,d)的子代。 BP神经网络[8-10]是指基于误差反向传播算法的多层前馈神经网络,它在负荷预测过程中采用梯度下降法来调整权值和阈值,容易使算法陷入局部最优。ACPSO算法具有全局搜索能力强和收敛速度快的特点,为克服神经网络的缺点提供了可能。ACPSO训练神经网络的过程如图 1 所示。 假设神经网络输入层,隐含层和输出层的节点数分别为n,h,m,则变量维数D=n×h+m×h+h+m。用式(6)均方误差公式(适应度函数)衡量每个粒子的适应值。 (8) 图1 ACPSO-BP流程图 本文所使用的数据由广东某地区实际电网提供,为该地区2011年历史负荷数据,一天拥有288个数据样本,时间分辨率为5 min。 小波分解(wavelet decomposition,WD)是一种把原始信号分解成多个子序列的数学方法,而且每次只对低频部分Ai(i=1,2,…)进行再分解[11]。小波分解一个信号f(t)时可表述如下: 图2 三层小波包分解结构图 表示共轭复数,‘a’是一个比例系数,‘b’是一个转换系数。小波分解对高频分量D进一步的剖分,这种固定的分解方式对不同的分解目的而言不一定能达到最优的分解效果。小波包分解(wavelet packet decomposition,WPD)则有效的解决了上述问题。假设S为原始负荷时间序列,Di(i=1,2,…)为高频子序列,在同一级尺度上小波包分解能同时对低频和高频部分进行分解,形成一个完整二叉树结构,如图 2所示,分解得到2j个子序列,j为分解层数,也就是尺度数。 综合考虑总体计算速度和预测精度,本文采用试错法多次实验,最后确定对原始负荷序列采用3层小波包分解。以5天数据样本点为例,共1 440点,进行3层小波包分解,结果如图 3所示。 图3 负荷时间序列的小波包分解 本文对负荷预测建模采用WPD-ACPSO- NN模型,并与WPD-BP-NN,WPD-PSO-NN,WD-BP-NN,WD-ACPSO-NN,WD-PSO-NN作比较。所提的混合算法模型如图4所示。该模型首先利用小波/小波包分解将原始负荷时间序列分解成多个频率的子序列,然后运用 PSO-NN/ACPSO-NN预测模型对各子序列进行预测,最后叠加各子序列的预测值,得到实际预测结果。 图4 基于混合算法的负荷预测模型 采用第3节中的2011年负荷数据进行时间分辨率为1 h的预测仿真。神经网络的参数如下:输入层、隐含层和输出层节点数分别为32、6和24;训练代数为100代;学习速率为 0.1;目标误差为 0.01。加速因子c1、c2的值设为2,惯性权重w值设为0.4,阈值λ取5×10-6,解空间维数设为D=32*6+6*24+ 6+24=336,种群大小设为M=50,最大迭代次数设为Maxgen=500。 为了有效和全面地评价各预测模型的准确率,分别采用平均绝对百分比误差MAPE。 (9) 分别采用3.2节中6种混合预测模型对典型工作日、典型周末和典型节假日三种不同的日类型进行预测,并分别对不同预测模型进行30次独立实验,神经网络的训练样本为预测日前90天的数据,不同预测模型的最优预测结果如图5~图7所示,表1给出了30次实验误差的平均值。 由图5~图7可见:(1)负荷曲线的每个拐点均为高频分量幅值较大的时刻,实验表明,WPD-ACPSO-NN预测结果比 WPD-PSO- NN、WPD-BP-NN更接近实际值。 (2)WPD-ACPSO-NN模型不仅保证了大多数预测点与实测负荷的偏离程度较小,而且在负荷序列的拐点处,能有效捕捉冲击负荷的变化规律,预测结果具有更高的精度。 图5 某典型工作日负荷预测曲线 图6 某典型周日负荷预测曲线 图7 某典型节假日负荷预测曲线 由表1可知:(1)对比WD/WPD-PSO/ ACPSO-NN与 WD/WPD-BP-NN,前者明显具有更高的预测精度,说明经优化后的神经网络能有效提高预测能力;(2)对比两种分解预测结果,经小波包分解后的预测精度明显优于小波分解后的预测,说明经小波包分解更有利于提高预测精度;(3)WPD-ACPSO-NN是所有混合模型中表现最好的,与WPD-BP-NN模型相比,该模型的MAPE分别减小了2.10%、1.38%、1.36%,有效提高了负荷预测的整体精度。 表1 不同类型日的预测结果误差分析 为了检验WPD-ACPSO-NN模型的泛化能力和稳定性,对该地区每个季节(选取2011年3月、6月、9月、12月)前3天进行连续预测。不同季节的误差分析结果如表2所示。 表2 不同季节的预测结果误差分析 由表2可知,WPD-ACPSO-BP模型在不同季节中的预测均取得较高的精度,最大百分比误差为2.16%,最小为0.263%。12天的平均预测误差仅为0.839%,这充分说明该模型的稳定性和强大的泛化能力。 提出采用自适应交叉粒子群算法来优化神经网络的权值和阈值,利用ACPSO全局搜索能力强、收敛精度高的优点,构建ACPSO-NN的预测模型。实验证明: (1)ACPSO-NN比BP-NN、PSO-NN具有更高的预测精度,有效克服了神经网络的缺点,提高了其泛化能力。 (2)为进一步提高预测的精度,利用小波/小波包变换对负荷时间序列进行分解,使用实际电网数据验证了本模型的有效性,并与5种混合方法进行对比,实验结果表明,WPD-ACPSO-NN的预测结果更接近于真实值。 [1] 马哲,舒勤. 基于ESPRIT分解算法的短期电力负荷预测[J].电力系统保护与控制,2015,43(7): 90-96. [2] 崔和瑞,彭旭. 基于ARIMAX模型的夏季短期电力负荷预测[J]. 电力系统保护与控制,2015,43(4): 108-114. [4] 李龙,魏靖,黎灿兵,等. 基于人工神经网络的负荷模型预测[J]. 电工技术学报,2015, 30(8): 225-230. [5] YU F, XU X. A short-term load forecasting model of natural gas based on optimized genetic algorithm and improved BP neural network[J]. Applied Energy, 2014, 134(1): 102-113. [6] 谷云东,张素杰,冯君淑. 大用户电力负荷的多模型模糊综合预测 [J]. 电工技术学 报,2015, 30(23): 110-115. [7] NIKNAM T,AZADFARSANI E,JABBARI M. A new hybrid evolutionary algorithm based on new fuzzy adaptive PSO and NM algorithms for distribution feeder reconfiguration[J].Energy Conversion and M anagement,2012,54( 1) : 7-16. [8] 丁明,王磊,毕锐. 基于改进BP神经网络的光伏发电系统输出功率短期预测模型[J]. 电力系统保护与控制, 2012,40(11): 93-99. [9] 肖迁,李文华,李志刚,等. 基于改进的小波-BP神经网络的风速和风电功率预测[J]. 电力系统保护与控制,2014,42(15): 80-86. [10] KHWAJA A S, NAEEM M, ANPALAGAN A, et al. Improved short-term load forecasting using bagged neural networks[J]. Electric Power Systems Research, 2015, 125(3): 109-115. [11] 常黎,杨清舟,黄开斌. 一种基于小波变换和人工神经网络的风速预报方法[J]. 太阳能学报,2013,34(4):604-609. A Load Forecasting Model Combining WPD and ACPSO Kuang Weihong1, Dong Zhen2 (1.Guangzhou Power Engineering Design Institute Co. Ltd., Guangzhou Guangdong 510220, China,2. College of Automation, Guangdong University of Technology, Guangzhou Guangdong 510006, China) 10.3969/j.issn.1000-3886.2017.03.021 TM761 A 1000-3886(2017)03-0068-04 定稿日期: 2016-10-12 匡卫洪(1985-),男,湖南娄底人,工程师,硕士生,主要研究方向为电力系统及其自动化。 董朕(1990),男,河南信阳人,硕士生,主要研究方为人工智能算法在电力系统中的应用。1.2 交叉算子
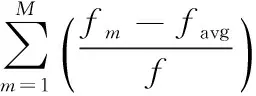
c1*[X(i,d)-X(j,d)]
c2*[X(j,d)-X(i,d)]2 ACPSO优化神经网络
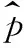
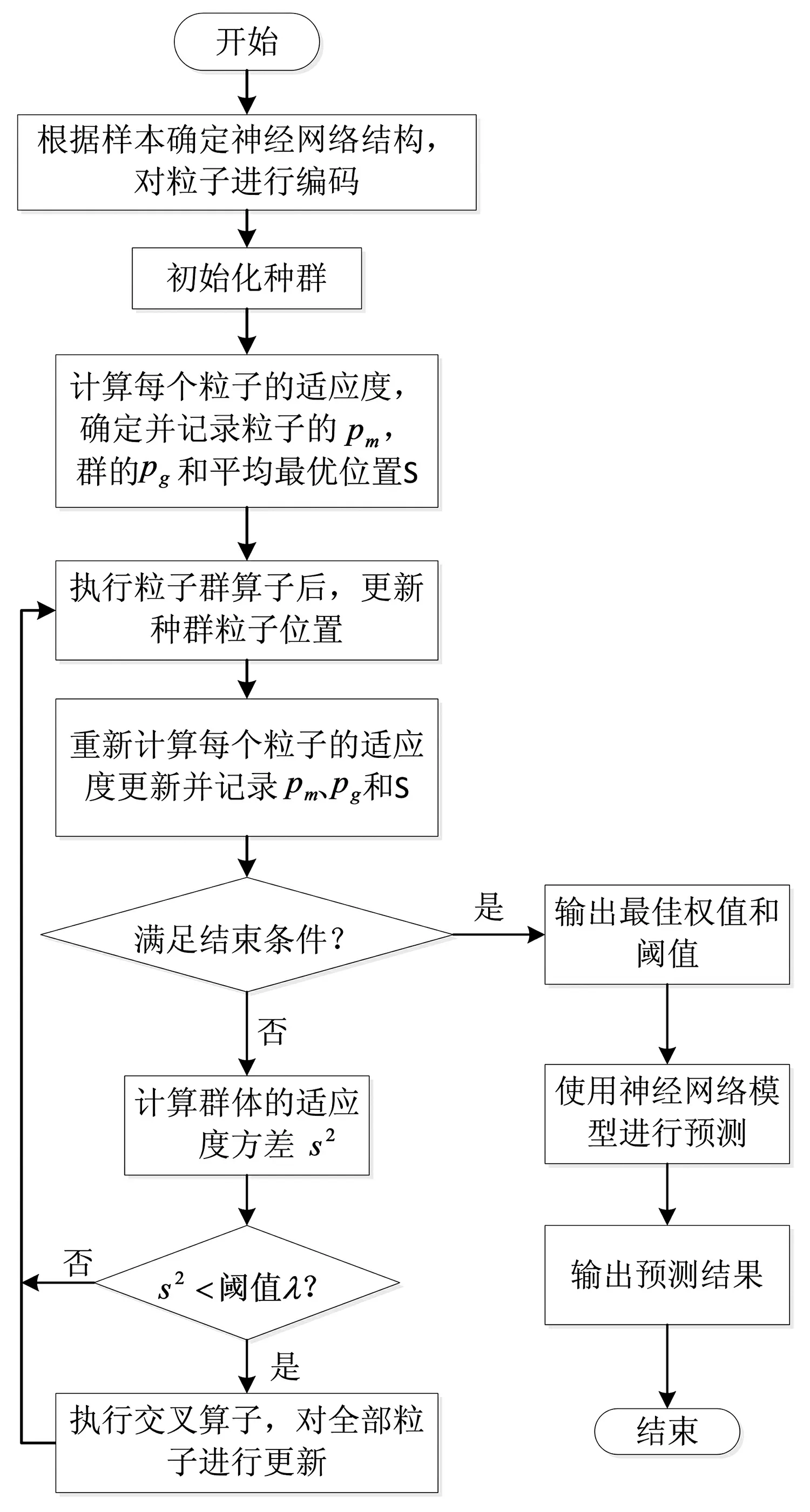
3 基于小波包和ACPSO-BP的预测模型
3.1 小波包分解
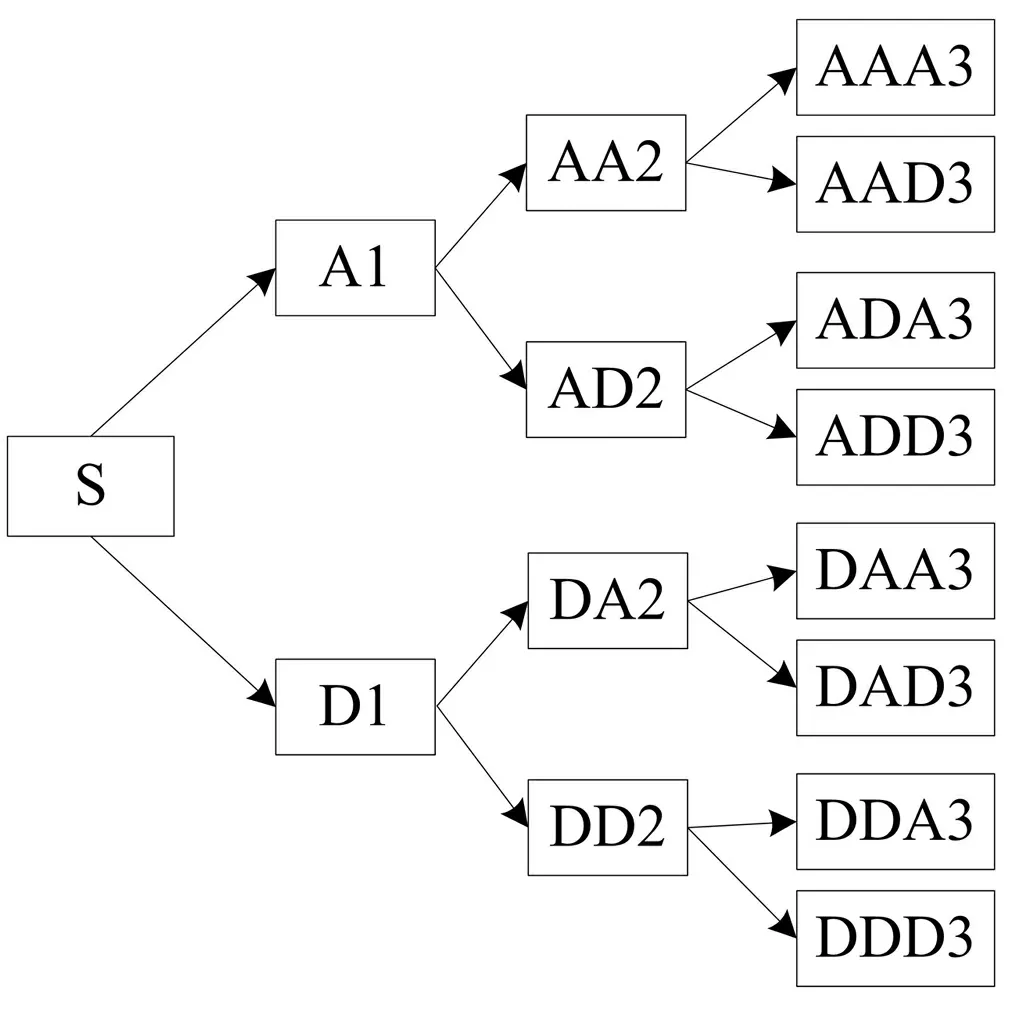

3.2 基于混合算法的负荷预测模型
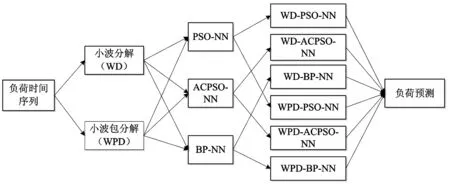
4 预测结果和对比分析
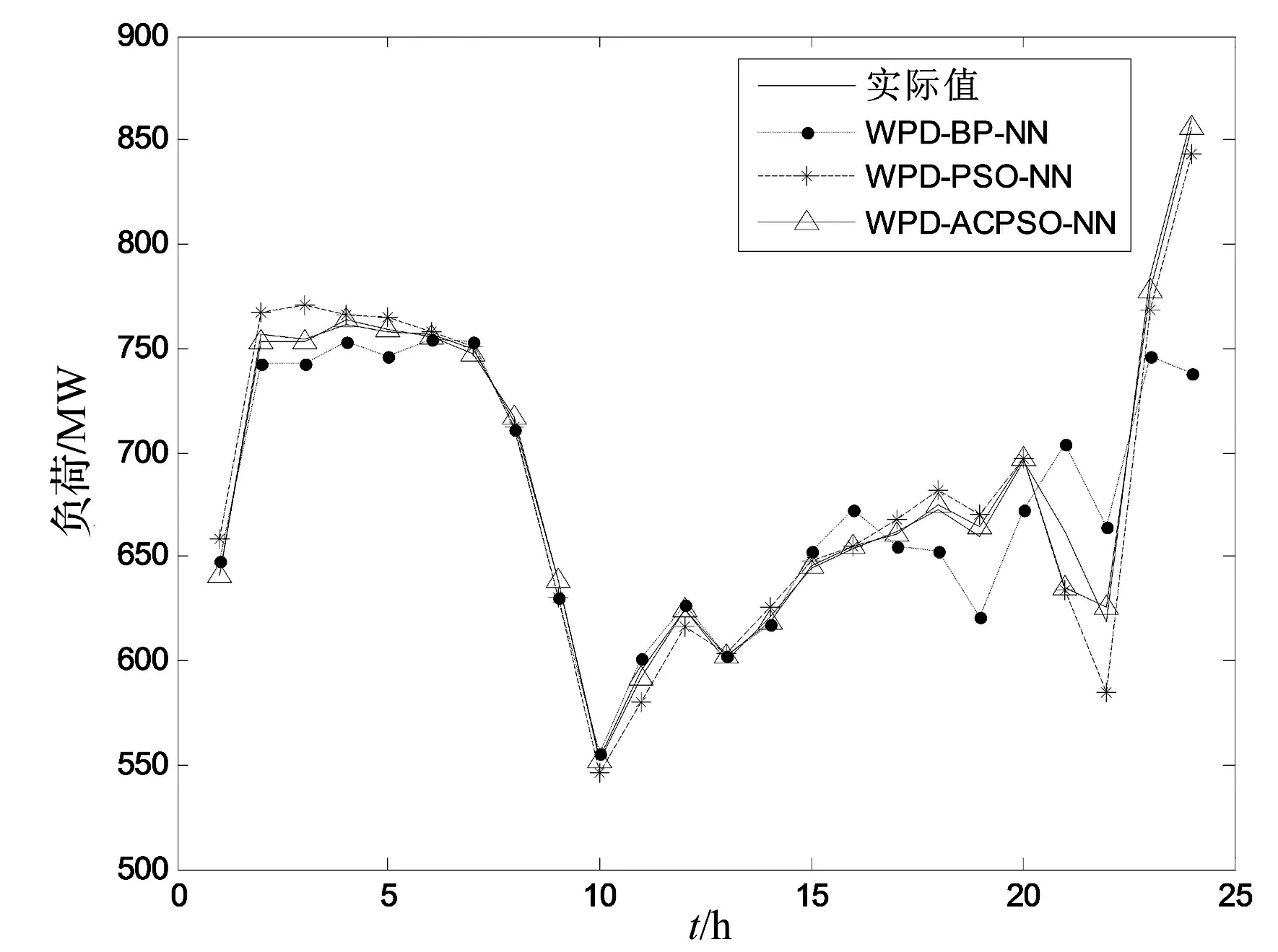
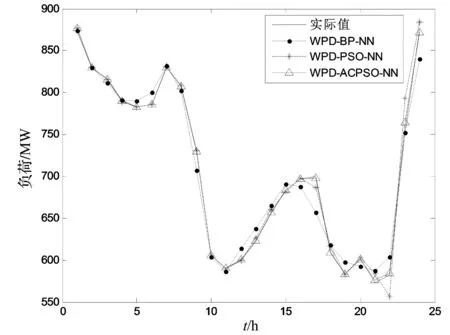


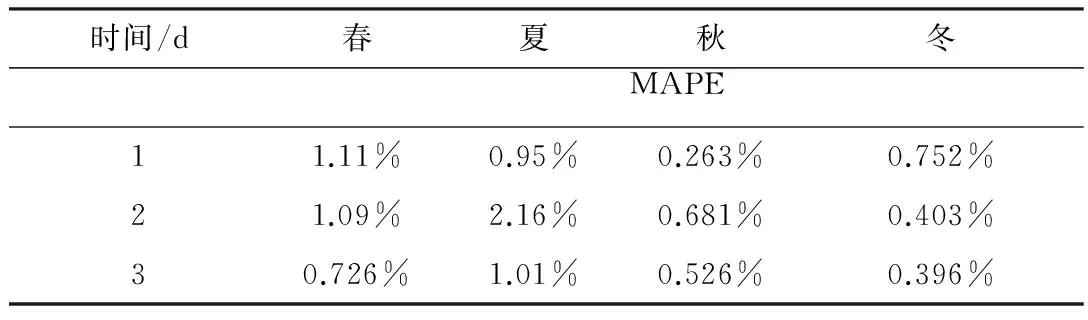
5 结束语
