住房需求的实证分析——基于我国31个省的截面数据

(云南财经大学 云南 昆明 650000)

住房需求的实证分析
——基于我国31个省的截面数据

张颖

(云南财经大学 云南 昆明 650000)

本文通过建立模型，选择全国31个省市的住房需求为研究对象，运用弹性模型，对住房需求和影响住房需求的因素用eviews-8进行回归分析。本文认为影响住宅需求的主要影响因素是居民的人口、人均可支配收入、房地产的价格。根据回归分析，验证了人口对住房需求有显著性的影响。

住房需求;异方差

一、影响住房需求的经济因素

住房问题可以说是和人民生活最密切的问题，但是，近几年随着房价的飞速上涨，住房问题成为了一部分人的很头痛的问题。住房需求分为私人住房需求和社会住房需求。本文将分析私人住房需求以及影响私人住房需求的主要因素。

(一)人口因素。显然，由于生活常识可知，人口越多，住房的需求也就越多。

(二)居民的人均可支配收入。居民的人均可支配收入是指在家庭总收入中，除去一切必要花费之外，居民可自由支配的部分。

(三)住房价格。总的来说，住房价格对住房的需求呈反方向的变化，即随着住房价格的提高，住房的价格会随之下降。

二、住房需求的实证研究

(一)计量经济模型和估计方法

本文设定的计量模型为弹性模型，即对被解释变量和解释变量同时取对数，选择弹性模型可以更加清晰的解释回归参数的意义，具体形式如下

ld=β0+β1lPop+β2lInc+β3lPrice+μ

(1)

设模型中的各解释变量如下表1。

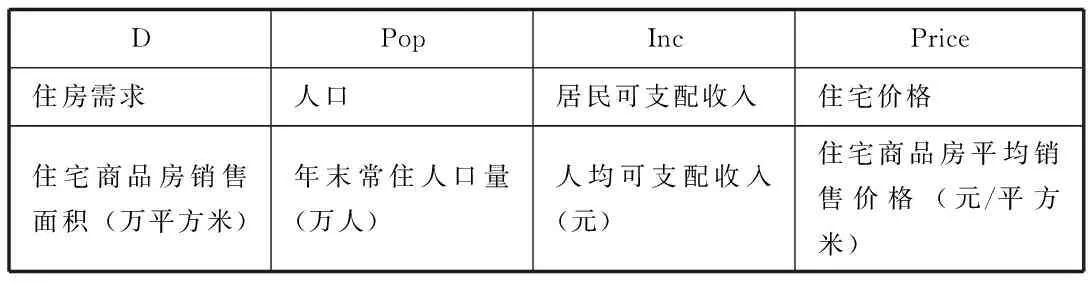
表1 解释变量与被解释变量描述

(二)数据

本文将采用2015年，全国31个省市的数据，现在给出每个变量的摘要统计量表，具体见下表2。

(三)结果

1、回归结果

基于上述模型，将上述数据用eviews-8进行ols回归，得到估计方程为:

ld=-6.811+1.158lpop+0.785linc-0.299lprice (2)

(2.42) (0.087) (0.505) (0.363)

(-2.814)(13.313) (1.554) (-0.826)

R2=0.891 N=31

从以上结果可以看出，整个模型的拟合优度为89.1%，说明整个模型拟合的较好，被解释变量即住房需求的89.1%可以由被解释变量解释。但是，在计量经济学中的多元回归分析中，我们不能过分强调拟合优度的作用。由回归结果可以看出，人口与截距的系数在5%的显著性水平下是十分显著的，价格和收入在5%的显著性水平下是统计不显著的，在这里，我们要区分统计显著和经济学上的显著，可能是由于样本统计的原因，尽管统计不显著，但是也不能在模型中被去掉。

由回归方程可以看出，人口的系数为1.158，涵义为在其他条件不变的情况下，人口每增加1%，住房需求增加1.158%；人均可支配收入的系数表明，在其他条件不变的情况下，人均可支配收入增加1%，住房需求增加0.785%，价格的系数为负，表明随着房价的上升，住房的需求下降，与经济学中的原理相符，价格的系数为-0.299，表明在其他条件不变的情况下，住房价格增加1%，住房需求下降0.299%。

2、假设检验

(1)单个总体参数的假设检验(t统计量)

原假设：H0:β1=0

备择假设：H1:β1≠0

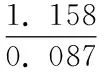
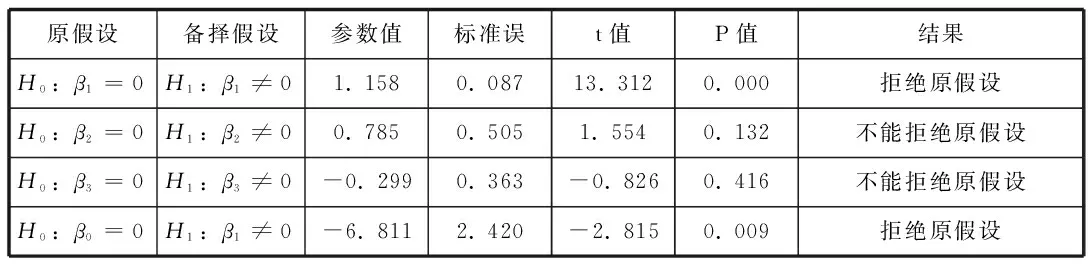
表3 单个总体参数的假设检验

(2)回归整体显著的假设检验(F统计量)

原假设：β1=β2=β3=0

备择假设：至少有一个βj不等于0

使用eviews-8软件可以自动报告模型的F统计量，由以上估计可以看出，整体显著检验的F值为73.34，P值为0.00，统计上十分显著，因此可以拒绝原假设。

3、异方差检验

(1)异方差稳健的t统计量

如图，对以上数据进行异方差稳健过程之后，得到如下结果，根据异方差稳健过程，回归的方程结果如下:

ld = -6.811 + 1.158lpop + 0.785linc - 0.299lprice (3)

(2.983) (0.130) (0.555) (0.438)

(-2.28) (8.380) (1.415) (-0.683)

R2=0.891 N=31

通过异方差稳健的标准误之后，与普通ols方法的回归之后的结果差别不大，说明模型的异方差问题不明显。

(2)异方差的BP检验

利用上述模型进行BP检验，结果如下，由上图可知，其辅助回归结果如下:

Resid2= 2.648 - 0.172pop - 0.247linc - 0.154lprice (4)

(1.088) (0.039) (0.227) (0.163)

(2.434) (-4.394) (-1.089) (0.944)

R2=0.496 N=31

对上述结果进行假设检验，异方差原假设：H0:σ2，即不存在异方差，异方差备择假设H1：即存在异方差。由回归结果可知，辅助回归的F值为8.843，其对应的P值为0.0003，在5%的显著性水平下统计显著，拒绝原假设，说明存在异方差。LM的值为15.36，其对应的P值为0.0015，在5%的显著性水平下统计显著，拒绝原假设，说明存在异方差。

(3)异方差的White检验

利用以上数据对模型进行包含交叉项的异方差的White检验，检验结果如下:

异方差原假设：H0:σ2，即不存在异方差。

由以上回归结果可知F=4.309，其对应的P值为0.0028，在5%的显著性水平下，拒绝原假设，即存在异方差。LM=20.111，其对应的P值为0.0172，在5%的显著性水平下，拒绝原假设，即存在异方差。White检验的结论与BP检验的结论一致。

(4)异方差的修正WLS估计

Resid2= 2.648 - 0.172pop - 0.247linc - 0.154lprice (4)

(1.088) (0.039) (0.227) (0.163)

(2.434) (-4.394) (-1.089) (0.944)

R2=0.496 N=31

由WLS方法回归得到的结果如下，

将用WLS方法修正后的结果进行异方差检验，检验方法仍然使用BP检验与White检验方法，检验结果如下。

(1)BP检验

由BP检验的结果可得，LM的值为12.83，其对应的P值为0.0016，在1%的显著性水平下统计显著，能拒绝原假设，说明wls方法在并没有消除异方差。

(2)White检验

由White检验的结果可得，LM的值为20.52，其对应的P值为0.015，在1%的显著性水平下统计不显著，不能拒绝原假设，说明wls方法在一定程度上消除了异方差。

三、结论

本文从影响住房需求的因素出发，影响住房需求的因素主要是人口因素、住房价格因素、人均可支配收入等因素。本文利用了2015年31个省市的住房需求数据，进一步分析了人口、住房价格、人均可支配收入对住房需求的影响。本文采用eviews8进行回归分析，并对截面数据进行了异方差的检验，最终消除了异方差带来的影响。验证了人口、住房价格、人均可支配收入对住房需求的显著影响。

张颖(1991-)，女，满族，河北省承德市，在读研究生，云南财经大学，城市与环境学院，区域经济学。