产出不确定下的双源采购模型研究

(浙江工业大学经贸管理学院 浙江 杭州 310023)

产出不确定下的双源采购模型研究

吴双

(浙江工业大学经贸管理学院 浙江 杭州 310023)

本文主要研究产出和需求不确定的环境下，由一个零售商和两个供应(其中一个为风险供应商)组成的二级供应链的订货模型。在批发价契约下，通过双方之间的博弈分析零售商的最优组合采购策略和影响零售商决策的因素。

产出不确定；需求不确定；双源采购；批发价契约

一、引言

产出不确定是引发供应链不确定性的重要因素之一。类似于电子信息类产品，服饰鞋靴以及农作物等季节性产品，由于质量精度，技术水平要求高，生产工艺程度复杂或者受到天气，人为灾害等不确定性因素的影响，其成品产出率经常表现出随机性和不确定性，导致企业极有可能发生产品缺货或者过剩而无法有效对接实际需求，从而对企业造成损失。因此，在供应链管理中，一方面我们要重视产出不确定带来所带来的风险防范，另一方面我们要采取合理有效的措施来降低供应链的损失。随着企业间竞争日益激烈，采购管理也变得尤为重要，尽可能地减少产品缺货以及库存积压不仅能够降低成本，增加利润，而且能有效降低供应链的资金周转风险。因此，双源采购被广泛应用于实际生产中，大多数企业为了不被单一供应商牵制，更重要地是减少减少供应不确定带来的风险，更愿意选择同时向两个或多个供应商进行采购。那么如何分配各个供应商之间的订单也成为零售商要思考的问题。

Dada(2007)等研究了有多个供应不确定供应商时的报童订货模型。从供应商的角度分析了影响零售商选择供应商以及下订单数的因素，表明了零售商在选择供应商的时候，考虑成本优先于供应商的可靠性，另外也证明了零售商所选供应商的订单大小取决于其可靠性。

Wang (2007)等在产出和需求都不确定的情况下，研究双源采购策略和改进供应商可靠性来降低供应风险的问题。通过分析不同情况下的最优组合策略和利润，给出了使用双源采购和改进供应商可靠性的条件。

Gurnani(2007)等研究了在需求确定和随机产出条件下装配系统的协调与合作问题，针对供应商可靠性较差的情况设计了一种惩罚机制来促进供应商交货的可靠性，尽可能满足零售商的订货量，减少供应风险。同时给出了实现系统协调的条件，确定最优组合订购策略。

二、模型构建与假设

该批发价契约模型中，供应商是Stackelberg领导者。首先，供应商1和供应商2分别确定自己的批发价格w1和w2；然后，零售商观察到供应商给定的批发价格后分别确定向两个供应商的采购数量Q1和Q2；销售季节开始前，供应商向零售商供货。供应商1和制造商2的生产成本分别为c1和c2，πs1，πs2表示供应商1和供应商2的利润。针对上述博弈问题，我们采用逆向归纳法来求解。

模型的参数：Q1，Q2为零售商分别向供应商1和供应商2下订单数量；ε1是供应商1产出随机因子，为定义在区间[0,1]上且服从均匀分布的随机变量；概率密度函数和累计分布函数为g(ε1)，g(ε1)；w1，,w2为供应商1和供应商2的批发价格；P为单位产品的零售价；g为零售商单位缺货损失；s为单位产品的残值；D为市场需求，为定义在区间[a,b]上且服从均匀分布的随机变量，概率密度函数和累计分布函数为f(x),F(x)。下标r，s1，s1分别表示零售商，供应商1和供应商2。

模型基本假设：(1)供应商和零售商都是风险中性决策者，均以自身利益最大化为原则进行决策 ；(2)供应商和零售商之间的信息是对称的；(3)P>w1>w2>s，这保证零售商是有利可图的。

三、基本模型求解

零售商的期望利润函数：

E(πr)={Pmin(ε1Q1+Q2,D)-w1Q1-w2Q2-g(D-ε1Q1-Q2)++s(ε1Q1+Q2-D)+}

(1)

对(1)中零售商的期望利润函数求导并求解，得到:

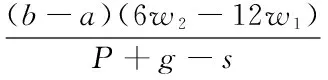
(2)

此时，供应商的期望利润函数为：

E(πs1)=(w1μ1-c1)Q1(w1))E(πs2)=(w2-c2)Q2(w2)

(3)

把(2)代入(3)得到供应商的最优批发价为：

(4)

把(4)代入(1)得到零售商的最优订货量为：

(5)

四、结论及未来研究方向

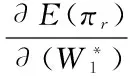
结论2：数值分析显示，需求的方差越大，不稳定性程度越高，零售商向不可靠供应商和可靠供应商的订货量都将增加以应对需求的不确定性。

未来我们可以考虑供应商均为风险供应商，但是供应商的可靠性程度不同，研究零售商的最有订货策略。

[1]Dada M, Petruzzi N C, Schwarz L B. A Newsvendor's Procurement Problem when Suppliers Are Unreliable[J]. Manufacturing & Service Operations Management, 2007, 9(1):9-32.

[2]Wang Y, Gilland W, Tomlin B. Mitigating Supply Risk: Dual Sourcing or Process Improvement[J]. Manufacturing & Service Operations Management, 2009, 12(3):489-510.

[3]Gurnani H, Gerchak Y. Coordination in decentralized assembly systems with uncertain component yields[J]. European Journal of Operational Research, 2007, 176(3):1559-1576.

吴双，女，研究生，浙江工业大学，研究方向供应链。