一种毛细管绝热流动模拟计算方法

张治涛，许雄文

( 1.国家知识产权局专利局专利审查协作河南中心，郑州 450002;2.华南理工大学电力学院，广州 510641 )

一种毛细管绝热流动模拟计算方法

张治涛1，许雄文2

( 1.国家知识产权局专利局专利审查协作河南中心，郑州 450002;2.华南理工大学电力学院，广州 510641 )

毛细管广泛应用于小型制冷装置中，其变工况工作能力差，需要与制冷系统进行优化匹配。本文提出了一种简单的可以通用的毛细管流量特性计算方法，可以在不同的阻力系数关联式下使用，并保证其具有较强的鲁棒性，推动毛细管流动特性模拟在工程中的应用。

毛细管；绝热；模拟

Abstract：The capillary tube is widely used in small refrigeration equipment.Due to its poor ability of working under variable condition,it′s important to match the capillary to the refrigeration system.This paper puts forward a simple calculation method for capillary flow performancein refrigeration.It gets strong robustness and can be applied with different flow resistance coefficientcorrelations,hopefully be applied in engineering.

Keywords：Capillary；Adiabatic；Simulation

1 引言

在家用冰箱、低温冷柜等小型制冷装置中，毛细管作为节流元件广泛使用。它结构简单、成本低。但变工况工作的能力较差,所以毛细管与制冷系统的匹配对系统制冷性能的好坏影响较大。

毛细管流动特性模拟方面已有较多的研究工作，主要分为两类，一类是采用离散型的分布参数计算法，另一类采用无量纲拟合流动关联式。第一类的研究工作比较多。西安交通大学高原根据均相流假设,用两相流基本方程建立了毛细管的数学模型,采用一种较为复杂的计算方法对绝热毛细管的流量特性进行数值模拟[1]。吕士济根据绝热毛细管中的压力降建立了一个适用于纯质制冷剂流过绝热毛细管的一维均相模型,用以计算毛细管的长度和其流动过程的热力性质变化，对传统制冷剂R12、R22、R134a、R152a在毛细管中的工作过程进行了详细的模拟计算，但其并未给出详细的计算流程[2]。第二类研究主要是韩国学者做得比较多。首尔大学(Seoul National University)Kim对R22，R407C和R410A在毛细管中的流动特性进行了实验，并采用量纲分析法进行量纲计算，得到了优化的无量纲计算关联式，对其他学者的实验数据进行了验算，计算误差在20%以内[3]。韩国大学(Korea University)Choi同样采用量纲分析法，基于Wolf[4]，Melo[5]，Kim[6]和Fiorelli[7]等人的实验数据进行无量纲分析，并拟合得到了无量纲的毛细管流量特性计算关联式，对这些实验数据的计算偏差在16%以内[8]。

对于毛细管流量特性的第一类研究工作，目前文献中建立的计算方法比较复杂，而且一般需要根据特定的计算式进行计算，使得工程应用比较困难。本文旨在提出一种简单的可以通用的毛细管流量特性计算方法，可以在不同的流量关联式下使用，并保证其具有较强的鲁棒性。

2 计算方法

2.1 控制方程

假设制冷剂在绝热毛细管内的流动为热力平衡下的一维均相流动，忽略重力的影响，其动量控制方程为：

(1)

其中，p,v,G分别表示流体的压力、比容、和质流密度(单位横截面积上的质量流量)，其单位分别为Pa,m3/kg,kg/(m2·s)；D和L为毛细管的内径和长度，单位为m；f为沿程阻力系数。等式右边的前半部分表示流动过程的静压对动压的转换，后半部分表示摩擦压降。

根据质量守恒，可得稳态时G为定值，不随流动变化。对于能量守恒，忽略其流动动能的影响，则可认为流动过程为等焓过程。

2.2 求解方法

2.2.1 物理模型

为保证求解的准确性，本文采用分布参数模型进行求解，毛细管沿其长度方向上等长度的离散如图1所示。

图1 毛细管沿长度方向离散

根据(1)式可得，

(2)

式中，下标in和out分别表示进出口参数；i和N如图1所示，表示离散点编号和总离散段数。则，

(3)

其中，

(4)

沿程阻力系数f的计算关联式有很多关联式可供选择，这里选取Blasius型关联式进行计算[9]，

f=aRe-b

(5)

式中，μ为动力粘度，Pa·s。对于两相粘度μTP的计算，采用McAdams模型进行计算[9]，

式中，x为干度，下标g,l分别代表饱和气相和饱和液相参数。

2.2.2 赋初值

本文假定已知进出口压力，过冷度及毛细管内径和长度计算其质量流量，若需求解其他参数求解思路相同。

初值假定毛细管内流体在每个离散段内的压降恒定，则可得到各离散点压力，

(6)

根据流体在毛细管的进口参数及等焓近似，根据压力的比焓可得到各离散点处的热力学参数，如比容vi等。根据经验，可令G0=2000kg/(m2·s)。

2.2.3 迭代流程

根据(3)式可得，以质流密度G作为不动点迭代参数，则，

(7)

另一方面，根据(1)式可得，每一个离散段的压降为，

(8)

(9)

综上所述，计算流程如图2所示。

图2 迭代流程图

3 结果分析与验证

3.1 收敛性分析

根据文献[5]数据回归，(5)式中沿程阻力系数计算时的控制参数取a=0.216,b=0.0823。毛细管模拟参数如表1所示，按照本文所述模拟方法进行计算，令G0取一个偏离解较远的值，则可得到其收敛曲线如图3所示。从图中可以看出，质流密度初值的选取可以有较大的范围，经过5次迭代即可取得满意的收敛结果，表明程序具有较好的鲁棒性和收敛效率。

表1 毛细管模拟参数

冷媒进口压力/bar过冷度/℃出口压力/bar管径/mm管长/mR134a926340980772926

3.2 计算结果分析

如上节所述，根据文献[5]式中沿程阻力系数计算时的控制参数取a=0.216,b=0.0823。则文献[5]中的实验值(工质为R12,R134a和R600a)与本文的计算值的偏差如图4所示。从图中可以看出，流量的实验值与计算值的偏差基本上都在±15%的范围内，准确性较高。将此计算式应用于文献[1]的实验值的验证，在制冷剂在毛细管进口过冷度小于10K的情况下，计算结果如表2所示，计算的偏差在20%以内，计算结果可以接受。

对于本文提出的毛细管计算流程，如果改变阻力系数计算关联式，计算过程依然可用。若能修正并改进阻力系数计算式，则可以得到更为准确的计算结果。

表2 文献[1]中的实验值与本文计算值的比较(D=0.66mm,L=5.5m)

冷媒进口压力/bar过冷度/℃出口压力/bar实验流量/kg/h计算流量/kg/h偏差(%)R134a110965208852023207-2%R134a110968708852033224-9%R134a110966608852027238-15%R134a110968808852033243-16%R134a110967408852029253＇-20%

图3 收敛过程

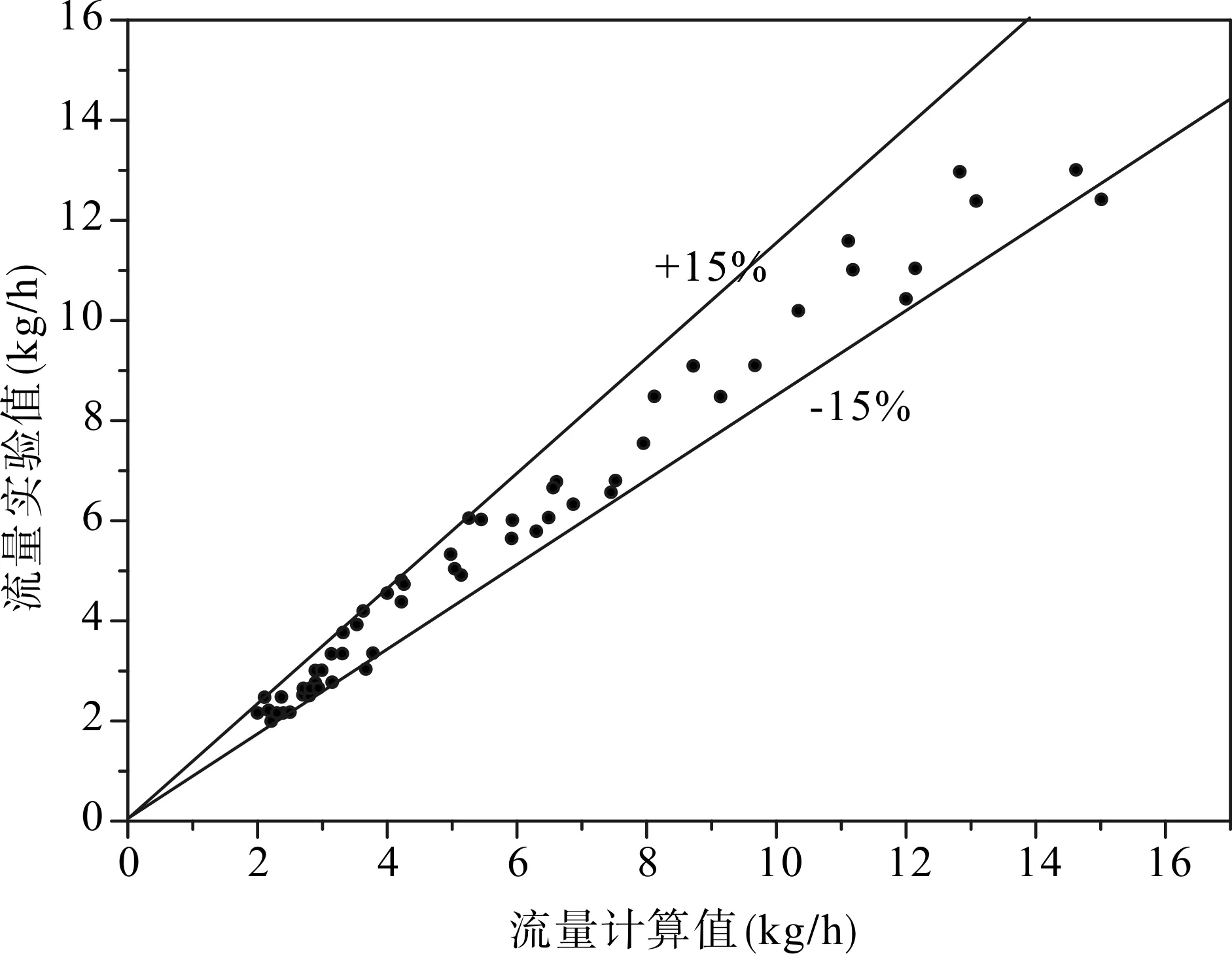
图4 偏差图

4 结论

本文提出了一种简单且具有较好收敛性的毛细管分布参数计算方法。程序计算结果表明，该计算流程具有较好的鲁棒性。

在此基础上，对文献[5]中的实验数据结合Blassiu型参数阻力系数关联式进行系数修正。并将此修正模型用于文献[1]中的数据验证，偏差为20%以内，计算结果可以接受。

对于本文提出的毛细管计算流程，如果改变阻力系数计算关联式，计算过程依然可用。若能修正并改进阻力系数计算式，则可以得到更为准确的计算结果。

[1] 高原,田怀璋,曾艳,等.用数值方法分析绝热毛细管的流量特性[J].流体机械,2002,30(7):47-49

[2] 吕士济,何茂刚,范德勤,等.替代制冷剂在绝热毛细管中流动的数值计算[J].工程热物理学报,2006,V27(3):365-368

[3] Kim S.G.,Kim M.S.,Ro S.T.Experimental investigation of the performance of R22,R407C and R410A in several capillary tubes for air-conditioners[J].International Journal of Refrigeration,2002,25(5):521-531

[4] Wolf D.A.,Bittle R.R.,Pate M.B.Adiabatic Capillary Tube Performance with Alternative Refrigerants[R].1995

[5] Melo C.,Ferreira R.T.S.,Neto C.B.,et al.An experimental analysis of adiabatic capillary tubes[J].Applied Thermal Engineering,1999,19(6):669-684

[6] Kim Y.C.,Cho I.Y.,Choi J.M.Experimentation and modeling on the flow of R407c and R290 through capillary tubes[J].Korean Journal of Air-Conditioning and Refrigeration Engineering,1999,11(4):492-498

[7] Fiorelli F.A.S.,Huerta A.A.S.,Silvares O.D.M.Experimental analysis of refrigerant mixtures flow through adiabatic capillary tubes[J].Experimental Thermal & Fluid Science,2002,26(5):499-512

[8] Choi J.,Kim Y.,Jin T.C.An empirical correlation and rating charts for the performance of adiabatic capillary tubes with alternative refrigerants[J].Applied Thermal Engineering,2004,24(1):29-41

[9] 丁国良,张春路.制冷空调装置智能仿真[M].北京：科学出版社,2002

ASimpleSimulationMethodforCapillaryFlowPerformanceinRefrigeration

ZHANG Zhitao1，XU Xiongwen2

( 1.Patent Examination Cooperation Center of the Patent Office,SIPO,Henan 450002; 2.School of Electric Power,South China University of Technology，Guangzhou 510641 )

2017-4-15

张治涛(1981-)，男，主要从事制冷空调专利审查。E-mail:37784101@qq.com

ISSN1005-9180(2017)03-070-04

TB657文献标示码B

10.3969/J.ISSN.1005-9180.2017.03.014