一种复杂脉内调制信号的识别算法

吴 昊，曹俊纺，王谦诚

(中国船舶重工集团公司第七二四研究所，南京 211153)

一种复杂脉内调制信号的识别算法

吴 昊，曹俊纺，王谦诚

(中国船舶重工集团公司第七二四研究所，南京 211153)

传统脉内特征分析算法具有只能识别较少调制类型的局限，本文提出一种可以分析带有脉内混合调制的复杂雷达信号识别算法。该算法先通过循环谱相关的分析方法对脉内调制类型进行粗识别，然后通过小波去噪预处理与小波变换的分析方法将混合调制信号转化为常见调制信号，最后通过频谱与二次方谱联合分析法将混合调制信号进行分类，实现了对多种复杂脉内调制信号的识别。仿真结果表明，在较低信噪比下该算法仍然具有较好的性能。

复杂脉内调制；识别算法；仿真分析

Abstract: The conventional in-pulse signature analysis algorithms have the limitation that the signals with only a few modulation types can be identified. A complex radar signal identification algorithm with in-pulse mixed modulation is proposed. Firstly, the in-pulse modulation types are identified roughly through the analysis method related to the cyclic spectrum. Secondly, the mixed modulation signals are converted to the common modulation signals through the analysis method of the wavelet de-noising preprocessing and the wavelet transform (WT). Finally, the mixed modulation signals are classified through the frequency and square spectrum combined analysis method, realizing the identification of various complex in-pulse modulation signals. The simulation results indicate that the algorithm still has good performance at a very low SNR.

Keywords: complex in-pulse modulation; identification algorithm; simulation analysis

0 引 言

随着雷达技术的发展，复杂调制信号越来越多，甚至出现了脉内混合调制的雷达信号。目前，国内外已有通过对复杂通信信号的研究提出对混合调制通信信号识别方法的相关文献记载，但通信设备上常用的混合AM调制和混合FM调制信号在雷达波形中并不采用，所以对复杂脉内调制的雷达信号进行分析与识别还需要进一步深入研究。

常用的雷达信号脉内特征分析方法可以分为时域分析法、频域分析法、时频域分析法和调制域分析法，主要有瞬时自相关、倒谱法、相位差分、STFT、WVD等方法。但是，这些传统方法经常与使用场合与应用条件相关，而不能适用于分析多种复杂雷达信号的脉内特征。本文提出了一种新算法，可以实现对常规信号(NS)、二相编码信号(BPSK)、四相编码信号(QPSK)、频率编码信号(FSK)、频率编码与二相编码组合(FSK-BPSK)、频率编码与四相编码组合(FSK-QPSK)等6种雷达信号的有效识别。实验表明，在较低的信噪比下该算法仍具有较高的识别准确率。

1 算法原理

1.1 信号模型

假设侦察接收机接收到的信号为

x(t)=s(t)+n(t), 0≤t≤T

(1)

其中，n(t)为均值为零、方差为σ2的平稳白噪声过程；T为信号持续时间；s(t)为雷达信号，其解析表达式为

s(t)=A(t)·exp(j(2πf0t+c(t)+φ0))

(2)

其中，f0为信号载频，φ0为初相，A(t)为幅度函数，c(t)为相位函数。不同的脉内调制类型体现在相位上，本文研究的雷达信号类型有：

(1) 常规信号(NS):c(t)=0；

(2) 相位编码信号(PSK):根据编码情况，BPSK的c(t)=0或π，QPSK的c(t)=0、π/2、π或3π/2；

(3) 频率编码信号(FSK): 根据编码情况，各子码上的载频f0产生相应的改变，而c(t)=0；

(4) 混合调制信号(FSK-PSK)：雷达系统的脉内混合调制是将发射的宽脉冲分为多个子脉冲，在频率编码的基础上再在各个子脉冲内进行各自的随机窄带调制。频率编码与二相编码组合的信号(FSK-BPSK)是在频率编码信号的各子脉冲内进行相应的二相编码调制，频率编码与四相编码的组合(FSK-QPSK)是在频率编码信号的各子脉冲内采用四相编码调制。

1.2 雷达信号的粗识别

雷达信号具有周期平稳性。设一周期平稳过程的循环自相关函数为

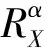
(3)

(4)

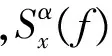
把NS信号、BPSK信号、QPSK信号称作第1类信号，把具有频率编码成分的信号(FSK信号、混合调制信号)称作第2类信号。分别以NS信号和FSK信号为例，给出这两大类雷达信号的循环谱图对比，见图1。

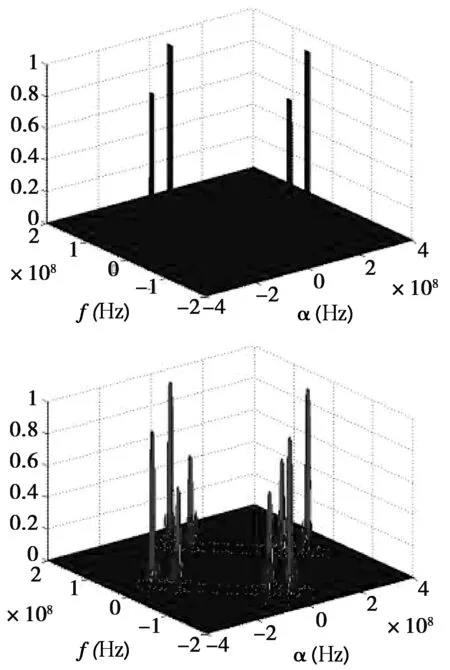
图1 两大类信号的循环谱密度函数图

由图1可以看出雷达信号的循环谱关于f=0和α=0对称。可以把谱峰个数作为特征值进行粗识别：第1类信号α截面的谱峰数为两个，第2类信号α截面的谱峰数大于两个。在采用离散频域平滑方法求得雷达信号循环谱之前，本文先对时域信号加窗处理，这样减少循环周期图的谱泄漏，使低信噪比条件下的谱峰个数判断更准确。

通过循环谱相关算法先将两大类信号进行区分，为后一步混合调制信号的识别作了必要准备。

1.3 脉内混合调制类型的识别

在识别脉内混合调制类型之前，先要把第2类信号FSK、FSK-BPSK、FSK-QPSK中由频率编码引起的频率跳变点找出，将信号分解成一系列的子信号，而每一段的子信号都可以看作脉宽较窄的NS、BPSK、QPSK信号。

本文先利用多重相位差分得到第2类信号的瞬时频率：

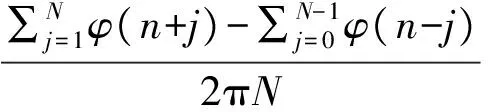
(5)

对瞬时频率作预处理。本文在大量实验的基础上，采用了小波去噪、中值滤波的预处理，然后再进行小波变换可以查找出频率跳变点。小波变换定义如下：

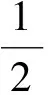
(6)

其中，a表示时间尺度，b表示时间上的位移。选择Haar小波基，因为其简单方便并且对短时信号尤其是存在相位变化的信号具有较强的检测能力。将信号与Haar基作内积，通过公式化简，可以定义信号瞬时频率f(n)的离散最小二进制Haar小波变换模为

(7)

从化简后的公式可以看出小波变换模的极值点对应信号的瞬时频率的跳变点。而经过小波去噪和中值滤波预处理过后的信号瞬时频率已减少了噪声和PSK的相位突变带来的影响，所以小波变换模的极值点可以直接判定为第2类信号的频率跳变点。

以信噪比8 dB条件下FSK-BPSK信号为例，频率跳变点的检测如图2所示。

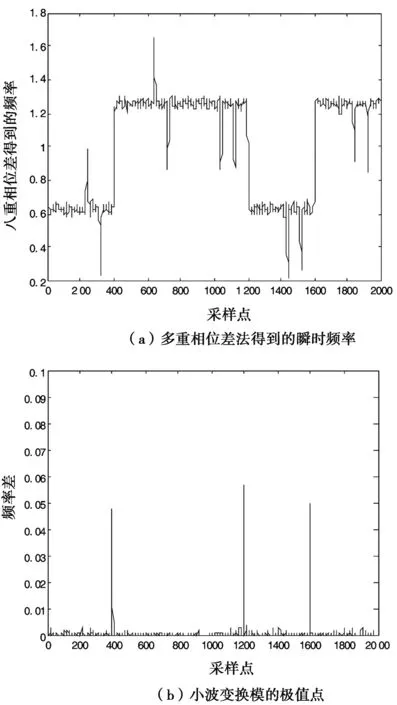
图2 信号的频率跳变点检测

由图2可以分析出，第400、1 200、1 600个采样点是FSK-BPSK信号的频率跳变点。

由上述方法查找到第2类信号的频率跳变点位置。把信号切分成若干个单载频的子信号，那么对这些子信号可以采用识别PSK常用的频谱与二次方谱联合分析的方法[1]，具体算法步骤这里不再赘述。当输入的信号为混合调制信号时，该方法可以识别子信号上的PSK调制，从而最终达到识别出混合调制类型的目的。

2 仿真分析

2.1 算法流程

基于本文的算法，完整的脉内调制类型识别流程如图3所示。

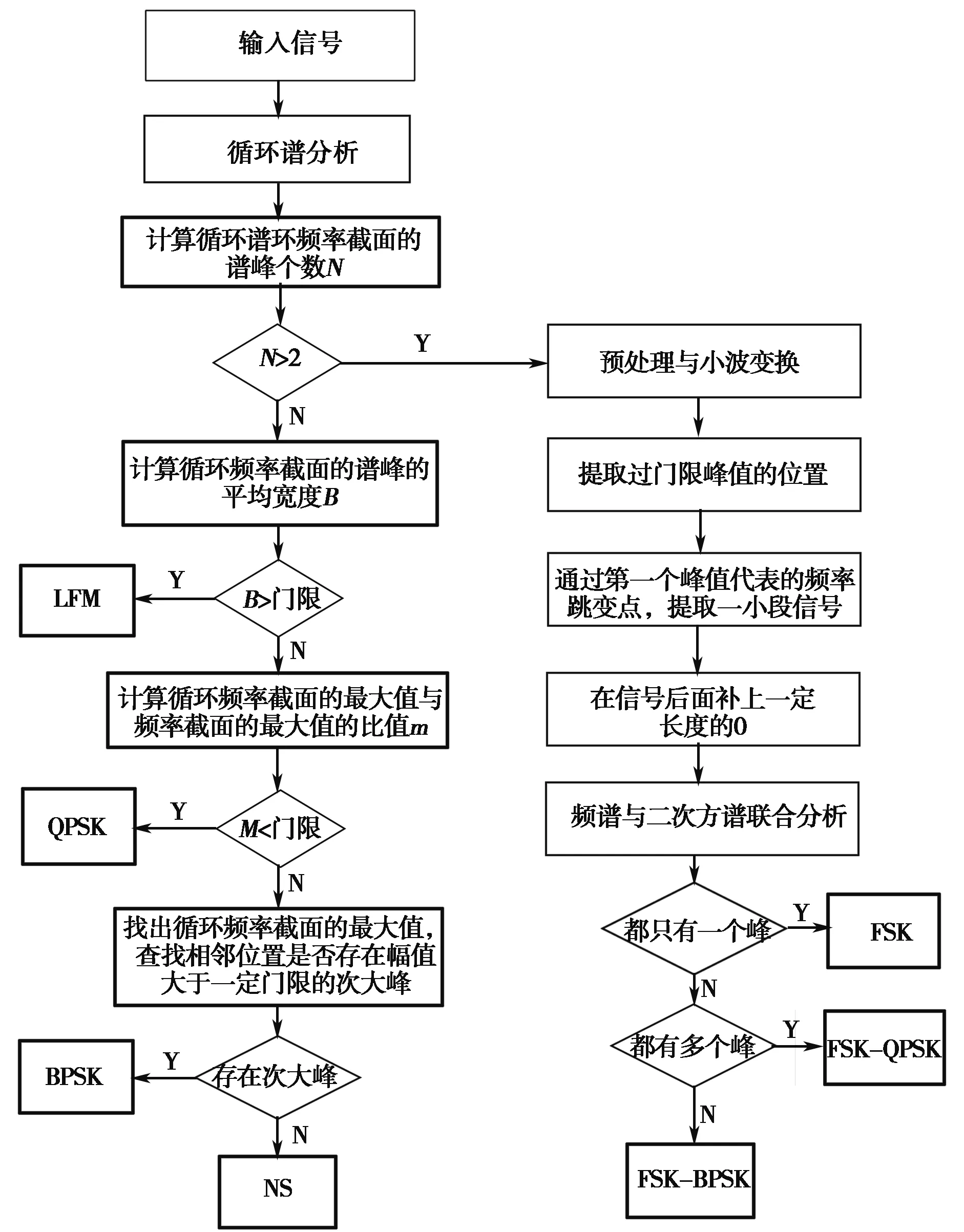
图3 完整的脉内识别流程

2.2 仿真验证

仿真验证采样频率为200 MHz，6种雷达信号参数如下：

(1) NS信号：载频30 MHz，脉宽10 μs；

(2) BPSK信号：载频20 MHz，脉宽14 μs，相位码组为7位Bark码：[0,0,0,1,1,0,1]；

(3) QPSK信号：载频20 MHz，脉宽16 μs，相位码组为16位Frank码：[0,0,0,0,0,1,2,3,0,2,0,2,0,3,2,1]；

(4) FSK信号：载频20、30 MHz，脉宽10 μs，频率码组为5位随机码；

(5) FSK-BPSK信号：载频20、40 MHz，脉宽10 μs，频率码组为5位随机码，每段子码上采用7位Bark码的二相编码；

(6) FSK-QPSK信号：载频20、40 MHz，脉宽10 μs，频率码组为5位随机码，每段子码上采用16位Frank码的四相编码。

基于本文的算法对每种信号在不同信噪比下分别进行500次Monte Carlo实验，识别准确率见图4。

图4 不同信噪比下的识别准确率

由图4可以看出，本文的算法在信噪比不低于5 dB时对各种信号的识别准确率都大于90%；在信噪比不低于0 dB时基本能准确识别调制类型；在信噪比低于0 dB时无法完成信号识别。

再以BPSK、QPSK和混合调制信号为例，将本文方法与文献[3]方法的识别准确率进行对比，如图5所示。

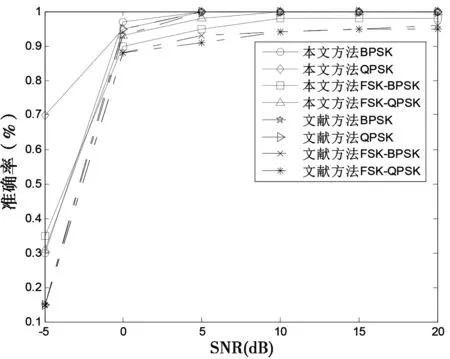
图5 识别准确率的对比

由图5可以发现，在低信噪比下，本文方法比文献方法的识别准确率高，其主要原因如下：

(1) 文献中对于识别BPSK与QPSK信号仅仅用了二次方谱进行区分，而在低信噪比下BPSK信号的二次方谱受噪声影响会出现多谱峰现象，造成谱峰阈值不好确定，BPSK与QPSK容易混淆。本文用的循环谱相关法则是通过循环频率峰值与频率峰值的比值作为特征值来比较，QPSK的该特征值明显小于BPSK的特征值，所以在低信噪比下对PSK信号的识别准确率依然较高。

(2) 本文对于混合调制信号先预处理，比文献多做了小波去噪的操作，提取的频率跳变点更加精确；然后对于提取出的子信号进行了补零操作，目的是将子信号增长至最接近的2的幂次方的长度，再对其进行频谱与二次方谱的联合分析，使得频率特性更加细致，提高了识别准确率。

3 结束语

本文提出了一种复杂脉内调制信号的识别算法。首先通过循环谱方法将信号分成两大类，并且分析识别了第1类信号的调制类型，然后通过小波去噪等预处理与小波变换模的极值点分析，提取第2类信号中的小段单载频信号，再利用频谱与二次方谱联合分析法将第2类信号中的调制类型进行有效识别。实验结果表明，即使在较低的信噪比下，该算法依然具有较高的识别准确率。下一步要做的工作是降低算法的复杂度，使该算法具有工程实现意义。

[1] 杨发权，李赞，罗中良. 混合调制信号识别方法[J].中山大学学报(自然科学版)，2014,53(1)：42-46.

[2] 徐伟，陈矛，张冠杰. 基于时频二维的雷达信号脉内调制识别方法[J]. 火控雷达技术，2011,40(1)：29-33.

[3] 李明晏，张鲁筠，江铭炎，许建华，张超. 复杂脉内调制雷达信号的识别方法[J].计算机工程与应用，2011，47(15)：156-161.

An identification algorithm of complex in-pulse modulation signals

WU Hao, CAO Jun-fang, WANG Qian-cheng

(No.724 Research Institute of CSIC, Nanjing 211153)

TN957.51

A

1009-0401(2017)03-0027-04

2017-10-28;

2017-07-26

吴昊(1990-)，男，助理工程师，硕士，研究方向：数据处理；曹俊纺(1976-)，女，高级工程师，硕士，研究方向：雷达信号处理、被动信号探测等；王谦诚(1983-)，男，工程师，硕士，研究方向：信号与数据处理。