多机电力系统的神经滑模励磁控制
2017-09-30牟奕丞肖健梅王锡淮
牟奕丞 肖健梅 王锡淮
多机电力系统的神经滑模励磁控制
牟奕丞 肖健梅 王锡淮
(上海海事大学,上海 201306)
电力是现代人类社会必不可少的部分,为了满足人类生活需要和经济发展,电力系统的稳定运行至关重要。本文结合自适应Backstepping方法和RBF神经网络,设计神经滑模励磁控制器,在Matlab/Simulink上进行仿真。为了验证控制器效果,加入三相短路故障,仿真结果表明了设计的神经滑模励磁控制器可以有效地提高系统稳定性,具有良好的鲁棒性。
滑模变结构控制 电力系统 自适应Backstepping 神经网络
0 引言
电力是现代社会和人民生活不可缺少的部分,为了保障居民稳定的生活,减少电力系统停电所带来的损失,电力系统运行首要的要求就是安全稳定。最早为了实现电力系统的稳定控制,建立电力系统的数学模型时,先将其进行近似线性化,再采用经典控制理论或者线性系统控制的相关理论来设计控制律。比如,早期的电力系统稳定器(PSS)以及线性最优控制方法都能在小扰动干扰下很好的稳定低频振荡,得到较好的稳定性,但是在较大的扰动下,难以到达理想的稳定状态,这是因为早期研究电力系统控制时采用近似线性化方法来建立系统模型,但是其忽略了电力系统的非线性和未知参数。所以,为了提高电力系统的稳定性,必须将电力系统归为非线性模型,并开始研究各种非线性控制策略,从而设计了各种非线性控制器。因此,反馈线性化[1]、鲁棒控制、自适应控制[2]、Lyapunov直接控制法[3]、变结构控制[4]、智能控制等控制方法越来越多地被运用到电力系统的研究中去。
本文针对多机电力系统,考虑系统的参数不确定性,通过适当的坐标变换将原数学模型转化为方便励磁控制器设计的严格参数反馈形式。滑模变结构控制存在抖振,因此为了消除抖振,学者将其与其它智能控制结合起来。滑模控制器使系统具有快速跟踪性,而神经网络又具备强大的学习能力和较好的稳定性。因此神经滑模控制可以在具有较好的系统鲁棒性的同时快速跟踪。最后,本文采用多机电力系统模型进行仿真并验证设计的控制器的鲁棒性与稳定性。
1 多机电力系统模型
在一些标准的假设下,通过一个传输网络的相互连接的发电机的动态可以用磁通衰减动力学模型描述的经典模型[5]。网络的内部总线已经减少,假设负载阻抗恒定并考虑转移电导存在。网第机的动力学模型是由经典的三阶模型表示。

其中
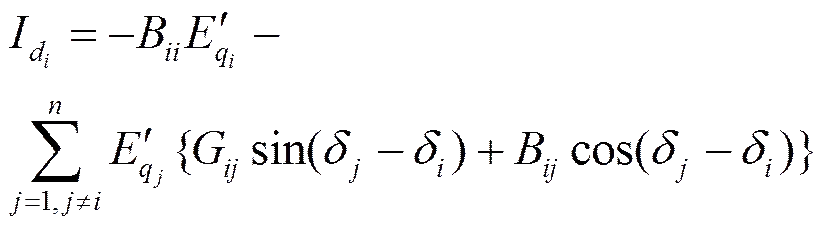
多机电力系统的第i个电机的状态表示可以写成以下形式:

其中:

2 神经滑模控制器设计
根据自适应Backstepping方法[6]设计控制器如下:
采用指数趋近率:

(4)
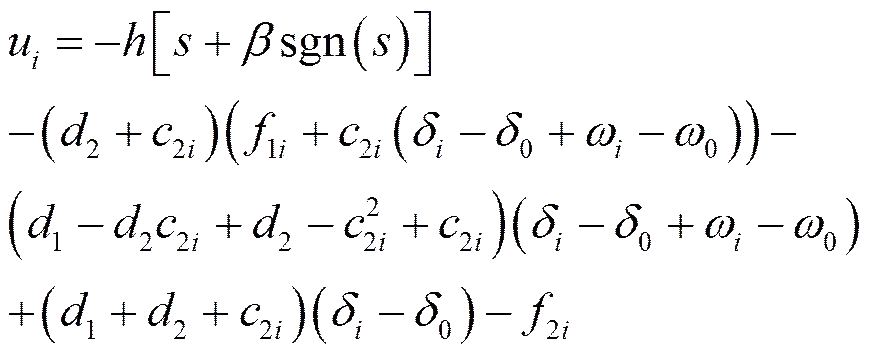
将滑模控制器设计为RBF网络的输出,即

其中为隐含层神经元个数。
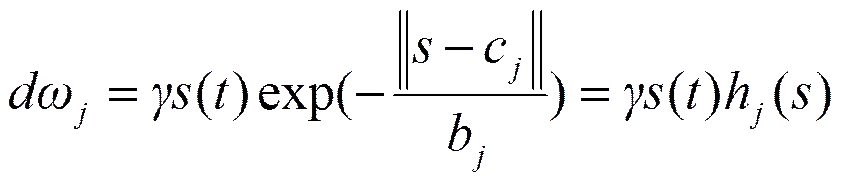
3 仿真分析
为了验证本文设计的滑模变结构励磁控制器的控制效果,对图1所示的3机9节点系统在Matlab/Simulink上进行动态仿真,只保留了发电机的内部节点,消除所有外部节点。
根据参数用s函数编写三个电机模型和三个电机控制器,三个电机的功角作为反馈量,假设系统初始状态为,3个发电机参数的数值在表1中给出。
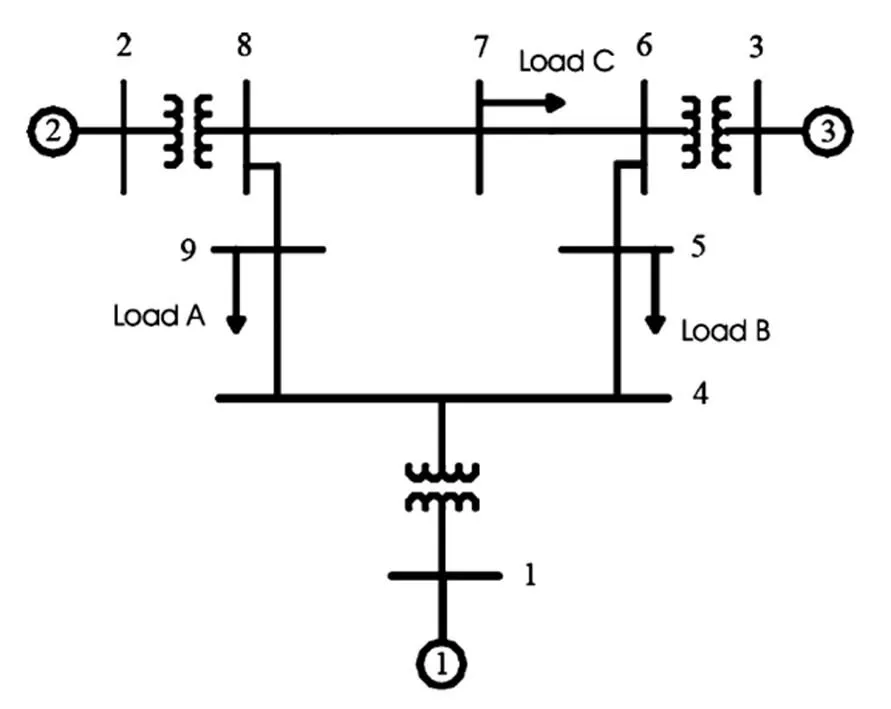
图1 三机9节点电力系统网络结构图
为了验证控制器在大干扰下的控制作用,在系统稳定后的9s时,节点8和节点9之间的线路上,在靠近节点9处发生三相短路故障,0.1s后故障移除。
网络的电导节点矩阵和电纳节点矩阵如下表示:
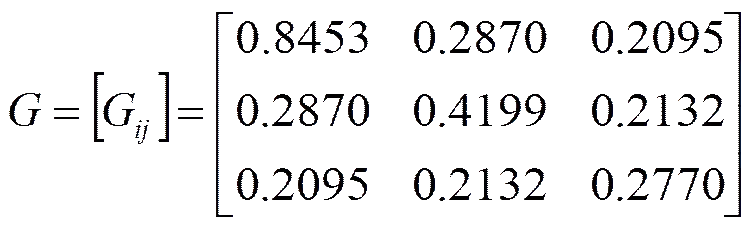
三相故障时,电导节点矩阵和电纳节点矩阵如下所示:
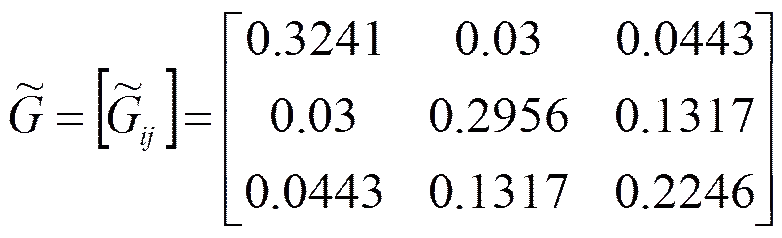
故障切除后,电导节点矩阵和电纳节点矩阵如下所示:
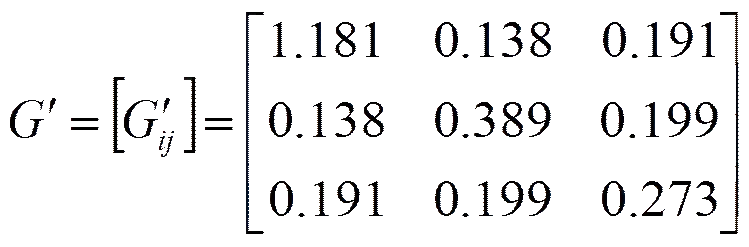
得到仿真结果如图1、2所示。
图中可见,5 s后3台发电机均达到稳定状态,9 s时,3台发电机功角和角速度偏差偏离稳定状态,但在1 s后均重新恢复稳定。
仿真结果表明,在神经滑模励磁控制器作用下,发电机启动后均能快速进入稳定状态。9 s时,三相故障发生在同步发电机机端时,该发电机不提供任何功率,而且由于欠阻尼作用,多机电力系统在故障切除后可能变得不稳定,仿真结果表明在三相短路故障后,功角和角速度偏差在神经滑模励磁控制器作用下迅速恢复稳定状态。说明神经滑模控制器具有良好的鲁棒性,提高了系统的动态品质。

图2 功角仿真结果图
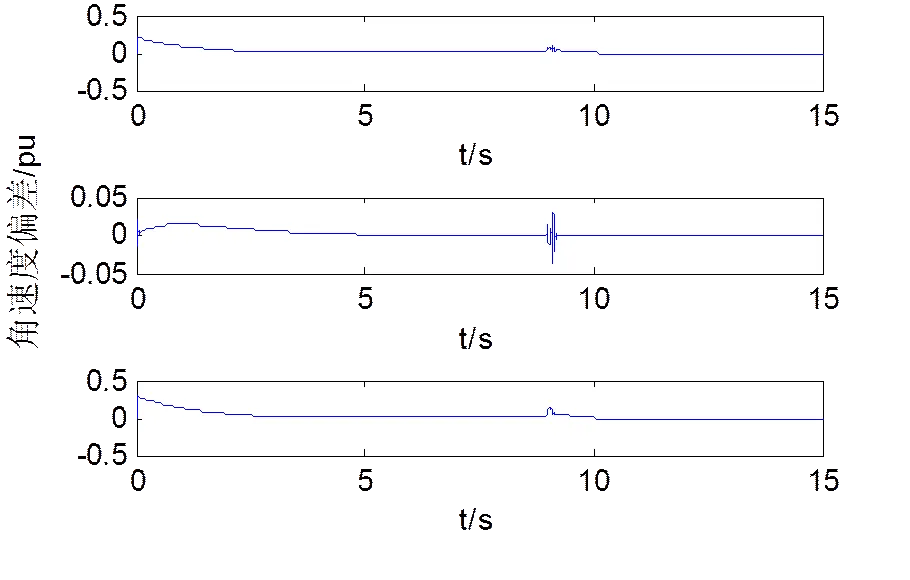
图3 角速度偏差仿真结果图
4 总结
本文分析复杂的电力系统的非线性模型并建立了便于设计控制器的3阶数学模型,基于Backstepping自适应法和神经网络,设计了神经网络滑模励磁控制器,在Matlab/Simulink上进行动态仿真,通过s函数编写发电机模型和控制器。仿真结果表明,三机电力系统具有较小的超调量和过渡时间,具有良好的鲁棒性,说明本文设计的神经滑模励磁控制器提高了电力系统动态品质,实现了稳定安全运行的要求。
[1] Cai J, Wen C, Su H. Adaptive inverse control for parametric strict feedback systems with unknown failures of hysteretic actuators. International Journal of Robust and Nonlinear Control, 2015, 25(6): 824-841.
[2] Yan Rui, Dong Zhao Yang, T.K. Saha, Rajat Majumder. A power system nonlinear adaptive decentralized controller design [J]. Automatica, 2010, 46(2): 330-336.
[3] Wang N, Liu H, Chen W. Lyapunov-based excitation control for the synchronous generator unit. Control Conference, 2013, 23(27): 89-903.
[4] Khaddouj Ben Meziane, Faiza Dib, Boumhidi Ismail. Fuzzy sliding mode control design and particle swarm optimization based PSS for multimachine power system. Research Journal of Applied Sciences, Engineering and Technology, 2014, 8(2): 188-196.
[5] M.A. Pai, Energy function analysis for power system stability, in: Kluwer International Series in Engineering and Computer Science. Power Electronics and Power Systems, Springer-Verlag, New York, 1989.
[6] 王亚坤, 孙丽颖, WANGYa-kun,等. 多机电力系统非线性自适应励磁控制器设计[J]. 辽宁工业大学学报(自然科学版), 2016, 36(2):71-77.
Neural Sliding Mode Excitation Control for Multimachine Power System
Mou Yicheng, Xiao Jianmei, Wang Xihuai
(Shanghai Maritime University,Shanghai 201306, China)
TM744
A
1003-4862(2017)09-0025-04
2017-07-15
牟奕丞(1994-),男,硕士研究生。研究方向:复杂系统控制与优化。
