基于几何平均数的风光互补发电系统MPPT控制策略研究
2017-09-30李源启陈雪亮王兴贵
李源启,陈雪亮,李 巍,王兴贵
基于几何平均数的风光互补发电系统MPPT控制策略研究
李源启1,陈雪亮2,李 巍1,王兴贵1
(1.兰州理工大学电气工程与信息工程学院,兰州 730050;2. 武汉船用电力推进装置研究所,武汉 430064)
根据风光互补发电系统的输出特性,研究了一种基于几何平均数的最大功率跟踪控制策略。首先,利用风力和光伏发电系统MPPT分别计算出下一时刻的电压占空比,然后利用几何平均数求出两个占空比的平均值。其次,用所求平均值控制风光互补发电系统的输出电压,从而保证风光互补发电系统工作在最大功率点。最后,通过MATLAB/Simulink进行了仿真分析,其结果验证了控制策略的有效性。
风光互补 最大功率 发电系统 几何平均数
0 引言
随着科技的高速发展,全球对能源的需求量与日俱增。风能和太阳能作为清洁性能源,已经受到国际上的广泛关注[1]。由于单个发电系统容易受到风速、光照强度等自然条件的制约和影响,只有将二者结合起来,才能扬长避短,提高发电效率[2]。
本文针对风光互补发电系统的输出特性,研究了一种基于几何平均数的最大功率跟踪控制策略。首先,利用风力、光伏发电系统MPPT控制策略计算出下一时刻的电压占空比。然后,用几何平均数求出这两个占空比的平均值,用求得的平均占空比值调整风光互补发电系统的输出电压,从而跟踪控制系统的输出功率。这样就可以实现用一个DC-DC电路同时跟踪控制风力和光伏发电系统的最大功率。进而保证风光互补发电系统工作在最大功率点。最后利用MATLAB软件对该控制策略进行了仿真,其结果验证了该控制策略的有效性。
1 基于同时跟踪最大功率跟踪控制策略
首先,利用风力和光伏发电系统MPPT分别计算出下一时刻的电压占空比。计算方法有:峰值功率跟踪法、爬山搜索法、扰动观察法、模糊控制法[3-7]。风光互补发电系统主要包括:风力机、光伏电池板、AC-DC整流电路、DC-DC升压电路、MPPT等。电路图如图1所示:

图1 风光互补发电系统电路
在统计学中,平均值的计算方法[8]通常有以下几种:
1)简单算术平均数
就是通常意义上的平均值,即

2)加权算术平均数
该计算方法主要通过各变量在数据中的权值决定,其表达式为
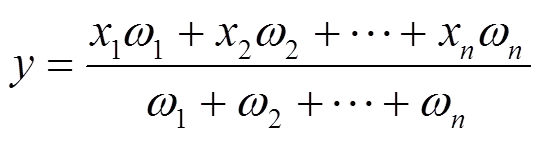
3)调和平均数
该方法也称倒数平均数,计算如下:
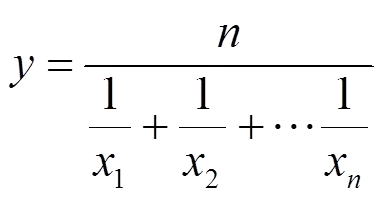
(4)

将式(4)代入式(5)中,有
(6)
式(6)中,由完全平方不等式,对于任何正数,有
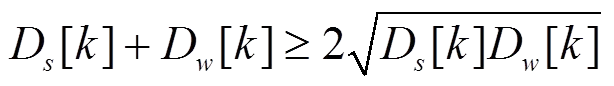
(8)
4)几何平均数

(10)
将式(10)代入式(5)可得

由此,几何平均数也适用于本系统。
基于以上分析,调和平均数与几何平均数都适用于风光互补发电系统对扰动步长的平均值计算,现取具体数值进行分析。
2 仿真分析
利用MATLAB/Simulink进行仿真,具体条件给定如下:

则风力发电系统、光伏发电系统、风光互补发电系统的输出功率如图2所示:

(a)风力发电系统
(b)光伏发电系统
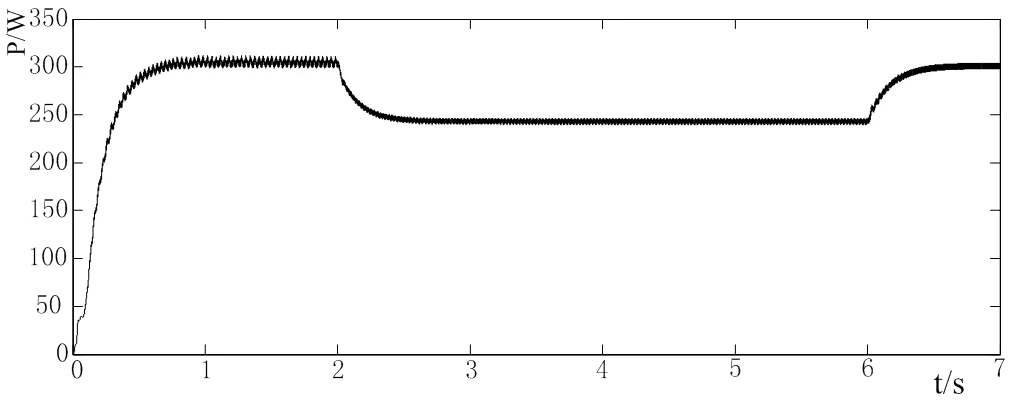
(c)风光互补发电系统
由于控制策略的原因,系统的输出功率会发生波动。取波动范围内的平均值作为分析依据。在第1s时,系统达到稳定状态。此时风光互补发电系统的理论输出功率为535 W,而实际输出功率为465 W,功率损失13%;第2s时,系统的理论输出功率为465 W,实际值为395 W,功率损失15%;第4 s时,理论值为540 W,实际值为480 W,损失11%;第6 s时,理论值、实际值、功率损失分别为470 W、435 W、7.4%。
通过以上数据可以看出,当风速或光伏发电系统的输出功率中只有其中一个值发生变化时,该控制策略会造成风光互补发电系统的输出功率损失较大。这是因为当只有某一个发电系统输出功率变化时,求几何平均值改变了扰动步长的大小,从而使得风力和光伏发电系统都没有工作在最大功率点。而当风速和光照强度同时变化时,即风力和光伏发电系统的输出功率同时发生变化,这种情况下,几何平均数法表现出了一定的适应能力,功率损失降低到了7.4%。
3 结论
在本文中,风光互补发电系统将风力发电系统和光伏发电系统的最大功率跟踪集中在一个系统中进行控制,结构简单,降低成本。在预测准确的情况下,所设计的控制策略可以在风速和光照强度的正常变化范围内快速跟踪风力和光伏发电系统的输出功率,从而保证风光互补发电系统工作在最大功率点。
[1] 刘艳. 可再生能源与新能源国际科技合作计划启动[J]. 能源工程, 2007, (06):42-43.
[2] 孙楠, 邢德山. 风光互补发电系统的发展与应用[J].山西电力, 2010,(4):54-56.
[3] 程启明,程尹曼,汪明媚. 风力发电系统中最大功率点跟踪方法的综述[J].华东电力,2010, 38(9):1393-1399.
[4] Zheng X M, Lin L I. Sliding-mode control of maximum power-point tracking in wind-power system for doubly-fed induction generator[J]. Control Theory And Applications, 2010.
[5] 邱革非,张春刚,仲泽坤. 基于扰动观察法和电导增量法的光伏发电系统MPPT算法研究综述[J]. 中国电力, 2017,50(3):154-160.
[6] Lee J, Kim Y S. Sensorless fuzzy-logic-based maximum power point tracking control for a small-scale wind power generation systems with a switched-mode rectifier[J]. IET Renewable Power Generation, 2016, 10(2):194-202.
[7] Chiu C S. T-S fuzzy maximum power point tracking control of solar power generation systems[J]. IEEE Transactions on Energy Conversion,2010, 25(4):1123-1132.
[8] 贾俊平. 统计学[M]. 北京: 清华大学出版社, 2004.
[9] 王兆安, 刘进军. 电力电子技术[M]. 北京:机械工业出版社, 2009.
Research on MPPT Control Strategy of Wind/solar Hybrid Generation System Based on Geometric Average
Li Yuanqi1, Chen Xueliang2, Li Wei1, Wang Xinggui1
(1.College of Electrical Engineering and information Engineering, Lanzhou university of Technology, Lanzhou 730050, China;2. Wuhan Institute of Marine Electric Propulsion, Wuhan 430064, China)
TM315
A
1003-4862(2017)09-0014-03
2017-06-15
李源启(1988-),男,硕士。研究方向:电力系统及其自动化。
