基于最大值滤波和数学形态学的弹性图像去噪

2017-09-28赵思雨张玉兰

电脑知识与技术 2017年24期

关键词：蠕虫形态学信噪比

赵思雨,张玉兰

(重庆人文科技学院计算机工程学院，重庆401524)

人工智能及识别技术

基于最大值滤波和数学形态学的弹性图像去噪

赵思雨,张玉兰

(重庆人文科技学院计算机工程学院，重庆401524)

数学形态学方法作为一种图像处理技术已经得到很广泛的应用，数学形态学理论也在不断发展和应用中日渐完善。数学形态学在图像去噪中的应用已经取得了很多可喜的研究成果。在数字图像去噪的研究中，研究者们经常会用中值滤波来对图像进行处理，鲜有用最大值滤波对含噪图像进行处理的，而最大值滤波有利于去除含噪图像中的暗点，从而使图像相对更加清晰。针对弹性图像蠕虫噪声的特点进行研究，提出了一种基于最大值滤波和数学形态学滤波相结合的弹性图像去噪方法。实验结果表明，和巴特沃斯低通滤波、中值滤波、小波阈值去噪相比，该方法不但取得了较好的去噪效果，而且获得了较高的信噪比(SNRe)和对比度噪声比(CNRe)，提高了弹性图像的质量。

数学形态学；最大值滤波；信噪比；对比度噪声比

图像在成像、传输过程中经常会产生各种各样的噪声，医学图像也不例外，也会产生各种噪声，图像去噪是图像预处理过程的一个重要环节，它不仅能够提高含噪声图像的信噪比，也会增强含噪图像的对比度噪声比，从而增强弹性图像处理前后视觉效果的对比度。弹性成像过程中通常使用长窗提高弹性图像的信噪比(singal-to-noise ratio，SNRe)，这时，为了获得高的轴向分辨率通常使用较高的数据窗重叠率。当重叠率大于90%甚至更高时，相关错误显著增加，产生所谓蠕虫伪像噪声使弹性图像质量显著下降[1]。

针对超声弹性图像蠕虫噪声的特点，王春光等[2]提出了一种基于编码激励的去除超声弹性图像蠕虫噪声的方法。该方法得到的超声弹性应变图像与传统方式相比，SNRe和CNRe都得到了较大提高，明显降低了噪声水平，但是在实验应用的过程中，出于不破坏信号横向分辨率和轴向相关性的考虑，必须适中地选择滤波器的个数。崔少国等[3]提出了一种使用二维小波收缩去噪法去除弹性成像蠕虫噪声的方法，该方法对不同应变量的弹性图像的蠕虫噪声均能有效抑制。

数学形态学方法作为一种用于数字图像处理和识别的新理论和新方法，它的理论虽然很复杂，但它的基本思想却是简单而完美的[4]，它比其他空域或频域图像处理和分析方法具有一些明显的优势。本文尝试将最大值滤波与数学形态学里的闭运算相结合的方法对含有蠕虫噪声的超声弹性图像进行去噪处理，不仅提高了图像的信噪比和对比度噪声比，而且提高了图像的清晰度和视觉质量，也为后续图像的分析和研究奠定了良好的基础。

1 理论基础

1.1 最大值滤波

二维统计顺序滤波是中值滤波的推广，对于给定的n个数值｛al,a2,...,an｝，将它们按大小顺序排列，将处于第k个位置的元素作为图像滤波输出，即序号为k的二维统计滤波。最大值滤波和中值滤波一样，都是二维顺序统计滤波的其中一种形式，简而言之，最大值滤波就是取出最大值作为滤波结果。最大值滤波可以扩大高灰度区域的影响范围，使图像在灰度级上实时膨胀，它在剔除胡椒噪声的图像去噪研究中具有很好的应用，比其他方法取得了更好的效果。

1.2 形态学理论

结构元素是数学形态学运算中的一个重要概念，它是膨胀和腐蚀的最基本组成部分，用于测试输入图像。二维或平面结构元素是一个包含0或1元素的数组，结构元素的原点是结构元素参与形态学运算的参考点，指定了图像中需要处理的像素范围，结构元素中数值为1的点决定结构元素的领域像素在进行膨胀或腐蚀操作时是否参与计算。

膨胀是将与物体接触的所有背景点合并到该物体中，使边界向外部扩张的过程。通过膨胀，可以填充图像中的小孔及在图像边缘处的小凹陷部分。结构元素B对图像A的膨胀，记作A⊕B,定义为

腐蚀与膨胀是对偶操作。腐蚀是一种消除边界点，使边界向内部收缩的过程。利用腐蚀操作，可以消除小且无意义的物体。集合A被结构元素B腐蚀，记作AΘB,

定义为：AΘB={x:Bx⊆A}

使用一个结构元素对图像进行膨胀运算，然后对结果进行腐蚀运算的运算方法称为闭运算，闭运算的符号为•。A用结构元素B的闭运算定义为A•B=(A⊕B)ΘB.闭运算可以平滑图像的轮廓，一般用闭运算来填充目标内的细小空洞和裂缝、连接断开的临近目标，其主要作用与膨胀作用相似，但与膨胀运算相比，具有可以基本保持目标物尺寸大小不变的优点。

2 方法

2.1 去噪方法

(1)先将带有蠕虫噪声的原始图像转化为灰度图像，设置显示图像的帆布大小为800×800，计算处理后图像的信噪比和对比度噪声比。

(2)用3×3大小的窗口对(1)中转化的灰度图像实现最大值滤波，并以octagon为结构元素、以6为半径进行闭运算操作处理，设置显示图像的帆布大小为800×800。

(3)利用弹性图像的信噪比公式和对比度噪声比公式计算(2)处理后所获得的图像的信噪比和对比度噪声比。

(4)分别利用巴特沃斯低通滤波、中值滤波、小波阈值滤波代替步骤(2)对从头开始对弹性图像进行(1)～(3)的操作，将其结果与本文方法进行比较。

2.2 性能指标

使用不同的方法对弹性图像进行去噪，实验结果可以用两个性能指标进行定量比较：弹性图像信噪比SNRe，弹性图像对比度噪声比CNRe[5]。

式中：μs和σs分别是均匀弹性区域应变图像的应变均值和应变标准方差。

弹性图像的对比度噪声比定义为：

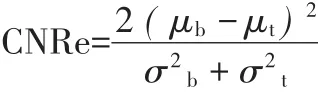
式中：μb和μt分别是背景和硬物的应变均值；σb和σt分别表示背景和硬物的应变标准方差。

3 实验及结果

本实验以带有蠕虫噪声的身体某部病变组织的图像为实验图像，将本文方法与巴特沃斯低通滤波、中值滤波、小波阈值滤波进行比较。本实验是在matlab 7.11平台下实现的，本实验将每次实验的输出图像与带有蠕虫噪声的原图像的SNRe和CNRe作为图像质量和去噪效果的评价指标，并且将通过本文方法所求得的SNRe和CNRe与巴特沃斯低通滤波、中值滤波、小波去噪三种去噪方法分别计算所得的SNRe和CNRe进行比较。

在实验过程中，采用不同方法进行实验所选取的硬物和背景的大小和区域都相同，为了保证每次由于系统显示不准确所造成的大小和区域不同的误差，设置图像显示的帆布大小为800×800。在实验中，对弹性图像进行巴特沃斯低通滤波选择的滤波器为2阶滤波器、滤波半径为50；对弹性图像进行中值滤波所选择的是3×3大小的窗口；小波阈值滤波是采用sym4小波函数，利用wdencmp函数对弹性图像进行小波软阈值处理；对弹性图像进行最大值滤波采用的是3×3大小的窗口，图像边界像素的处理是以用0对边界进行扩展的方式进行的，进行数学形态学闭运算滤波采用的是以octagon为结构元素、6为半径进行实验的。

在实验过程中，分别在图像左下角和黑色原斑中间取50×50大小的区域，并对所取的区域计算信噪比和对比度噪声比。(背景选取区域坐标为：[240,440,50,50];硬物选取区域坐标为：[388,290,50,50];)本文中的图像是对实验结果图像去除边缘非图像像素的白色区域的基础上获得的，获得的图像及图像的性能指标如下所示：

使用不同方法处理后的性能指标如下表所示：

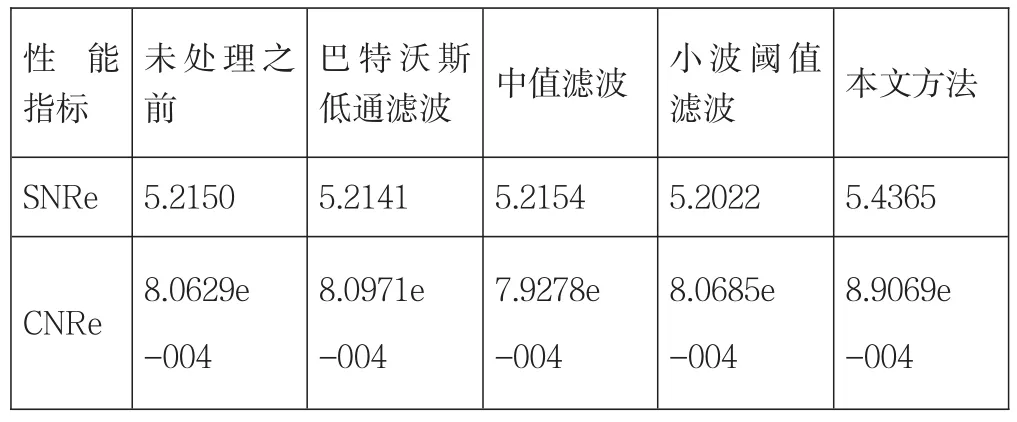
表1 弹性图像去噪后的评价指标

从实验结果可以看出，巴特沃思低通滤波和小波阈值滤波虽然可以提高含噪图像的对比度噪声比，但是其信噪比则比较低，而中值滤波虽然得到了较高的信噪比，但是它的对比度噪声比则比较低。最大值闭运算滤波不但使含噪图像的信噪比有明显提升，同时也使其对比度噪声比有很大的提高，获得了比以上三种方法更好地去噪效果，为医学诊断提供了良好的图像质量。