以离散元方法研究抄板对RDX-Al混合效果的影响

王正宏，林秋汉，李世伟，王彩玲，赵省向，李建良

(1.辽宁庆阳特种化工有限公司， 辽宁庆阳 111002； 2.南京理工大学 化工学院， 南京 210094； 3.西安近代化学研究所， 西安 710065)

【化学工程与材料科学】

以离散元方法研究抄板对RDX-Al混合效果的影响

王正宏1，林秋汉2，李世伟1，王彩玲3，赵省向3，李建良2

(1.辽宁庆阳特种化工有限公司， 辽宁庆阳 111002； 2.南京理工大学 化工学院， 南京 210094； 3.西安近代化学研究所， 西安 710065)

采用离散元软件模拟单元空间内的颗粒存在体系，对旋转筒内搅拌混合过程中颗粒变化情况进行数值模拟，并以此为基础研究抄板对黑索金-铝粉(RDX-Al )混合效果的影响。考察抄板的长度、设置角度、添加个数以及填充率等对搅拌均匀程度的影响，并给出其最佳参数。根据研究结果，发现了当抄板的长度和旋转筒内半径的比值在0.4、抄板与旋转筒内壁的距离同旋转筒内半径的比值为0.2时，搅拌混合的效果最好。当装填量为40%，且加入的抄板量为4(或5)个的时候，搅拌混合效果最好。抄板设置的角度为75°时，搅拌混合的效果最好，本论文的研究结果将为现实工业生产中对RDX-Al 的混合提供借鉴和指导。

离散元方法；颗粒混合效果；抄板；网格划分

工业生产中，混合炸药的混合在旋转筒中进行，为了提高混合效果，往往在旋转筒中安装片状板块，常称之为抄板。本论文旨在研究工业生产中黑索金-铝粉(RDX-Al )在旋转筒中的搅拌混合效果，给出抄板的最佳设置参数。论文采用离散元软件模拟单元空间内的颗粒存在体系，通过对旋转筒内搅拌混合过程中颗粒变化情况的模拟为基础，研究抄板对RDX-Al 混合效果的影响。考察抄板的长度、设置角度、添加个数以及填充率等对搅拌均匀程度产生的影响，并给出其最佳参数。

通过研究发现，加入抄板后颗粒数无明显变化，也可以说变化没有规则。但是，颗粒在前面的波动较大，后面的波动较小，也就是颗粒数的振荡逐渐变小，与颗粒的大小无关。因此，颗粒数一直在变动，并最终达到一个稳定值。加入抄板后会改变颗粒的稳定值，这是由于抄板的加入改变了原本的运动形式，使颗粒不产生分层，从而改善其混合效果。所以颗粒数最终为一个较为合理的值(该值代表空间内混合均匀度)[1-2]。

本研究工作所用到的硬件为2.4GHz四核 CPU，内存3.0G的计算机，操作系统为Windows7，软件开发平台是Visual C++6.0和matlab，用到软件EDEM[3-4]。本论文研究的初始条件，与文献[5]相同。

1 效果放大方法分析

通常所用的离散元方法最多只能模拟上千个颗粒的级别，差不多就是一个子空间规的规格。本文首先采用离散元方法进行模拟，并根据结果，用蒙特卡罗方法模拟得出相应规律，以子空间规为基础，将其中的颗粒变化作为依据推算到整个旋转筒中，再加入抄板进行模拟，变动抄板的长度和位置，进行分析和讨论，可以得到相应规律[6-8]。

首先将旋转筒划分成数个单元空间，将每个单元空间所能够容纳的颗粒数目的上限设置为相同，大约 1 000 个。在三维模拟中，旋转筒内的颗粒一般可以分为两类，第一类颗粒处于抄板的作用层，这一类所处的横向截面上具有抄板的作用。而第二类没有在抄板的作用层，在横向截面上没有受到抄板的作用。旋转筒的搅拌混合效果主要与前者的混合效果相关，即前者的混合效果对整个系统的的混合效果影响很大[9-10]。因此，本工作重点关注第一种颗粒的混合效果。

旋转筒内的混合程度与所划分的单元空间内的颗粒密度相关，故只需研究其中一个单元空间内的颗粒密度即可。根据文献[11-12]可知，最终混合效果与最初的颗粒的分布没有关系，可以假设颗粒数量的变化与其最初的分布关系较小。为了实现最佳的模拟效果，可以假设每个空间内的颗粒的数目变化只和相邻的单元内的颗粒数目有关，忽略其初始分布效果，从而确定单元内颗粒的变化情况。

在每一个时间步长内，进行如下处理：该空间和18个空间相邻，和相邻的七个空间形成一个较大的子空间，这样的子空间差不多有四个。对这四个子空间进行模拟，再由八个小空间组成较大的子空间中得到颗粒的初始分布和其运动情况。根据模拟得到一个步长的数据特别是一个步长后该空间颗粒转移到相邻空间中的个数值。根据四个空间的数据，就可以得到所研究的目标空间转移至邻空间的颗粒数量。对所有空间进行处理，就能得到每个时间步长后颗粒的变化情况，最后根据变化情况判定混合效果。

2 抄板样式

根据样本变异系数可以判定颗粒混合的效果，样本变异系数小说明混合的效果较佳。在研究抄板的安装位置以及其长度对混合效果影响时，可以模拟得到不同安装位置和长度下的变异系数，并根据参数的好坏来确定其最佳参数。

图1是抄板类型，通常是在两条相互垂直的横向轴所固定的圆环面上设置抄板。将抄板的外侧和旋转筒内壁的距离记为d1，内侧与旋转筒内壁的距离记为d2。抄板的长度值设为l，d1+d2+l=R。因此，颗粒的混合效果与d1，d2和l有关。

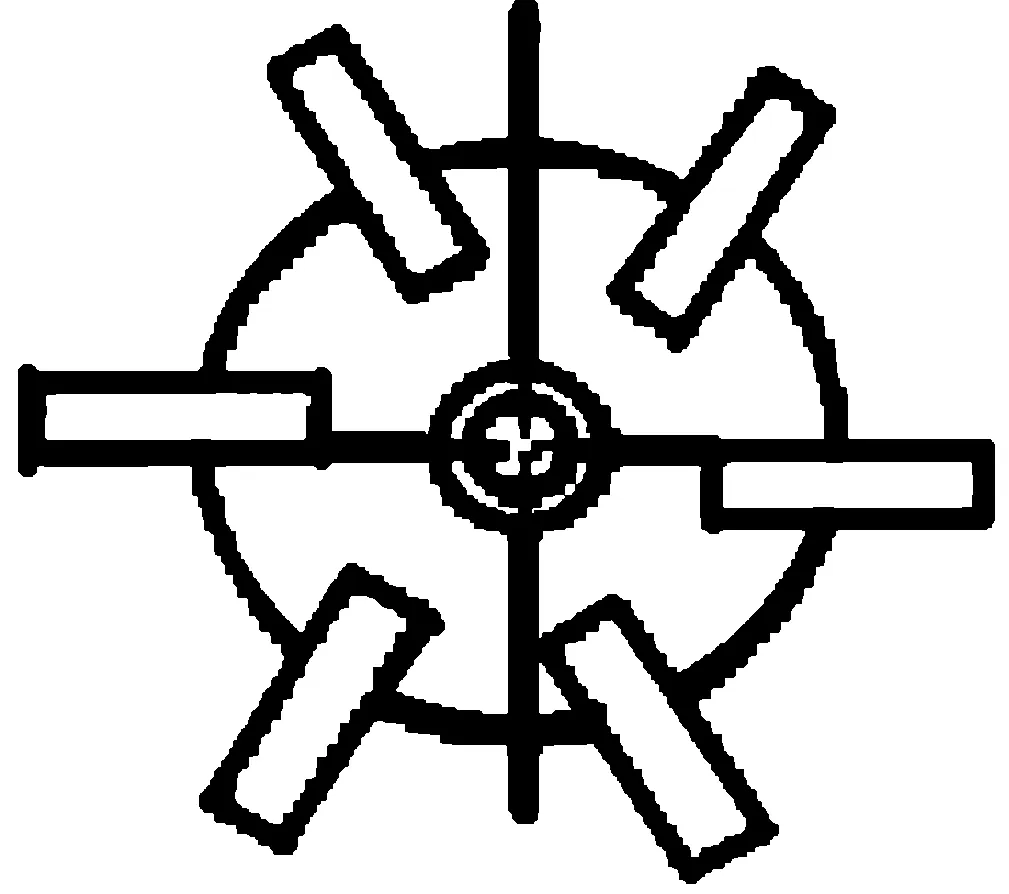
图1 抄板样式示意图

通过模拟，先得到抄板的最佳设置长度值，然后将其长度设置为恒值，接下来变换抄板和筒内壁的距离d1，找到d1的最佳值(同时也得到了d2的最佳值)。

从旋转筒的内壁开始，直到旋转筒的筒心设置抄板。每加上一个抄板，对其进行一次模拟，根据数值模拟结果给出足够大时间步长的颗粒混合均匀情况。这样，通过模拟可以获得与抄板长度对应的样本变异系数。根据这个变异系数即可确定抄板的最佳长度，作为具体生产的参考。

通过前述模拟获得抄板长度的最佳值后，将其设置成一个固定值。然后变化d1的大小(d1值所取的范围在[0,R-l]之间)，每一个d1都进行数值模拟，可以根据这个变异系数确定d1的最佳值。

(1)

L=2n-1

(2)

3 抄板长度与位置模拟分析

该模拟中，将旋转筒设置成多个环面，并且在每个环面上的初始颗粒数目一样，之后将颗粒的级数放大，可放大至数十万倍。具体地，将每层分割为2 500份(本论文模拟的放大效果约为十万倍)。根据所设置参数对每个抄板长度都进行数值模拟，其长度l为：

l=0.05·n·R

(3)

n取1到20之间的整数。

如图2所示，抄板长度从0开始增大，变异系数出现了明显的降低，也就是说颗粒的混合变得更均匀了(即混合效果变好了)，在抄板长度和旋转筒内半径的比值在0.4时，变异系数达到最小值。之后，随着其长度l的增大，变异系数变大，也就是说混合度开始变得不均匀了。根据图2的结果可以得到结论：最佳的抄板长度值为0.4R。

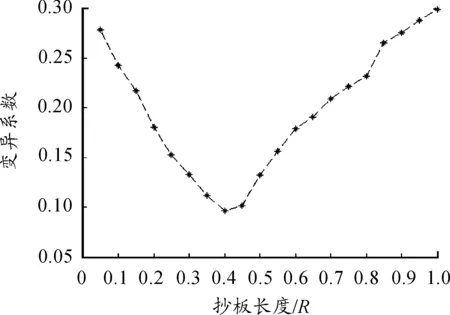
图2 抄板长度变化的数值实验结果

这一结果也符合常理，现实中被抄板作用到的部位，其中的颗粒运动比较激烈。抄板没有作用到的空间中，运动缓慢[13]。因此，抄板的长度变大，抄板作用的区域也随之变大，但是抄板侧划过的空间开始减少，因此，二者之间有一个平衡值，根据数值模拟得到的值为0.4R。之后，将抄板的长度值设置为0.4R，变化抄板外侧与筒内壁的距离d1再次进行数值模拟，求出不同d1值变化时的奇异系数。

数值模拟结果见图3，随着l的增大，颗粒的变异系数不断减小，当l值接近0.25R时，变异系数达到最小值。再往后，变异系数的值随着l的变长而变得越来越大。这一点说明l值增大，抄板作用到的空间减小，但抄板侧划过的空间内，开始随着l值的变长而增大，所以，最佳的l值不是0。根据数值模拟结果可得出结论，在抄板与旋转筒内壁的距离值约为0.25R时，具有最佳的搅拌混合效果。

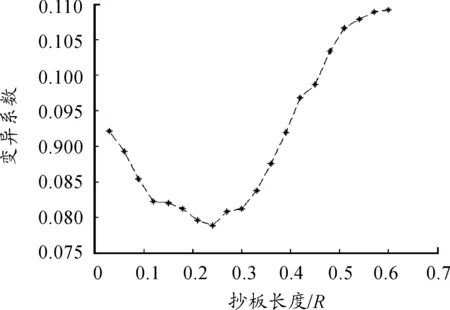
图3 抄板和旋转筒内壁距离变化的数值实验结果

4 抄板长度与位置模拟分析

4.1 抄板个数分析

在固定空间内，运动比较迟缓的空间颗粒互相交换比较少；颗粒交换较多的空间是活动空间，该空间内颗粒的运动速度较快。没加入抄板时，距离旋转筒内壁比较近的地方，颗粒的运动和交互更为活跃，也就是说离筒内壁近的地方是活跃的空间的可能性越大。由于颗粒在筒内壁的运动比较迟缓，加入抄板后，颗粒同抄板之间发生正面接触，因此靠近抄板的空间里的颗粒比较活跃，这一部分空间也称为活跃区域[14]。

可以认为每个抄板的加入对颗粒的混合效果影响与相应的模拟曲线有关。如图4所示，将颗粒的活动区域用一条曲线(该曲线与抄板的速度，高度即装填量有关)连接。

图4 抄抄板作用曲线示意图

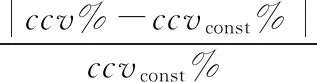
在旋转筒内添加抄板之后，抄板的介入使各类空间的kcv值发生了改变。受抄板影响大的空间集合，其kcv值明显大于1。受到抄板的影响不大的空间集合，其kcv值接近1。一般认为前述的第一类空间区域是抄板主要影响的区域，后一类空间所在的区域，抄板的影响较小。若一个抄板和另一个抄板的影响区域发生重合交叉，两个抄板可能相互影响搅拌效果，其作用发生一定程度的叠加。而一个抄板如果没有在另一个的影响区域内，二者是独立的，它们之间没有干涉。因此，不同的抄板之间应该相互独立才有利于更好的提高混合效果。由于抄板个数的选取和单个抄板影响的区域的大小相关，因，假如每个抄板所影响的空间与总体的比值为0.25，则抄板个数在4个时最佳，而在现实生产中，抄板个数通常设置为4～5个。

4.2 装填量分析

每一个抄板的对应曲线和抄板旋转速度以及颗粒的装填量都有关系，但是抄板在开始工作时的旋转速度是恒定值，所以对应曲线可以看作是只和颗粒的装填量相关。装填量随抄板高度的增加而变大。当抄板高度增加到一个定值的时侯，对应曲线不会再发生很大的变化。对应曲线与抄板影响的空间类数目有着必然的联系，因此，也可以说明当抄板高度增加到一个定值的时侯，其所能影响的空间数目就不再发生变化，如图6所示。

在图6中，左边是旋转筒，装满了RDX-Al 颗粒，右边是抄板。在旋转筒加入抄板时，抄板影响的区域如图6所示。抄板所能影响到的区域超过其自身高度，超过抄板高度的那一部分区域的大小是不变的，抄板的延长会使抄板高度内的影响区域变大。当抄板的高度接近颗粒装填的顶部后，其所影响的区域不再发生变化。若抄板高度再增加，例如增加至高于颗粒装填的顶部，则原来高于抄板的那一部分影响区域会减少以至消失。

当抄板高度还未到临界值时，kcv值会随着抄板高度的增高发生变化；而抄板高度达到一定值后，kcv值将不再发生变化。因此，研究不同高度的抄板时，分析其kcv值，如果kcv值的变化不大并趋于稳定，说明抄板的高度达到了临界值，继续增高已经没有意义。

4.3装填量、抄板个数对混合效果的模拟分析

在分析抄板的添加个数和颗粒的装填量时，需要结合二元颗粒分布特征，因此取前后两层的颗粒。纵高：其高度为五十个单元空间，在每个截面上有二层，即总共有50×2个单元空间。抄板高度的改变使得颗粒的装填量也发生改变，本文用数值模拟方法对每个不同的装填量对比研究，给出不同抄板高度不同装填量下的变化率，即kcv值。

kcv值代表奇异系数的增长率，是靠近底部的空间内的kcv值。由图7可知，当装填量接近或稍大于50%时，kcv值接近0。也就是说如果kcv值接近0，说明颗粒的搅拌混合桶没加入抄板时的状态相差不大。而装填量超过50%后，抄板对旋转筒底部空间的作用很小。此外，若装填量从0开始增加，如果此时的kcv值较大，可以判定抄板的作用很大。

图7 装填量变化的数值实验结果

通常可以认为kcv值小于0.1时，抄板的作用很小。因此由图7可以知道，最佳的装填量应该选在40%左右。将装填量设定为40%考察抄板个数，可知道抄本所能影响到的空间。若kcv值相对较大，可以说明抄板作用了到该区域中的颗粒；若kcv值接近0说明抄板对该区域中的颗粒的作用很小。

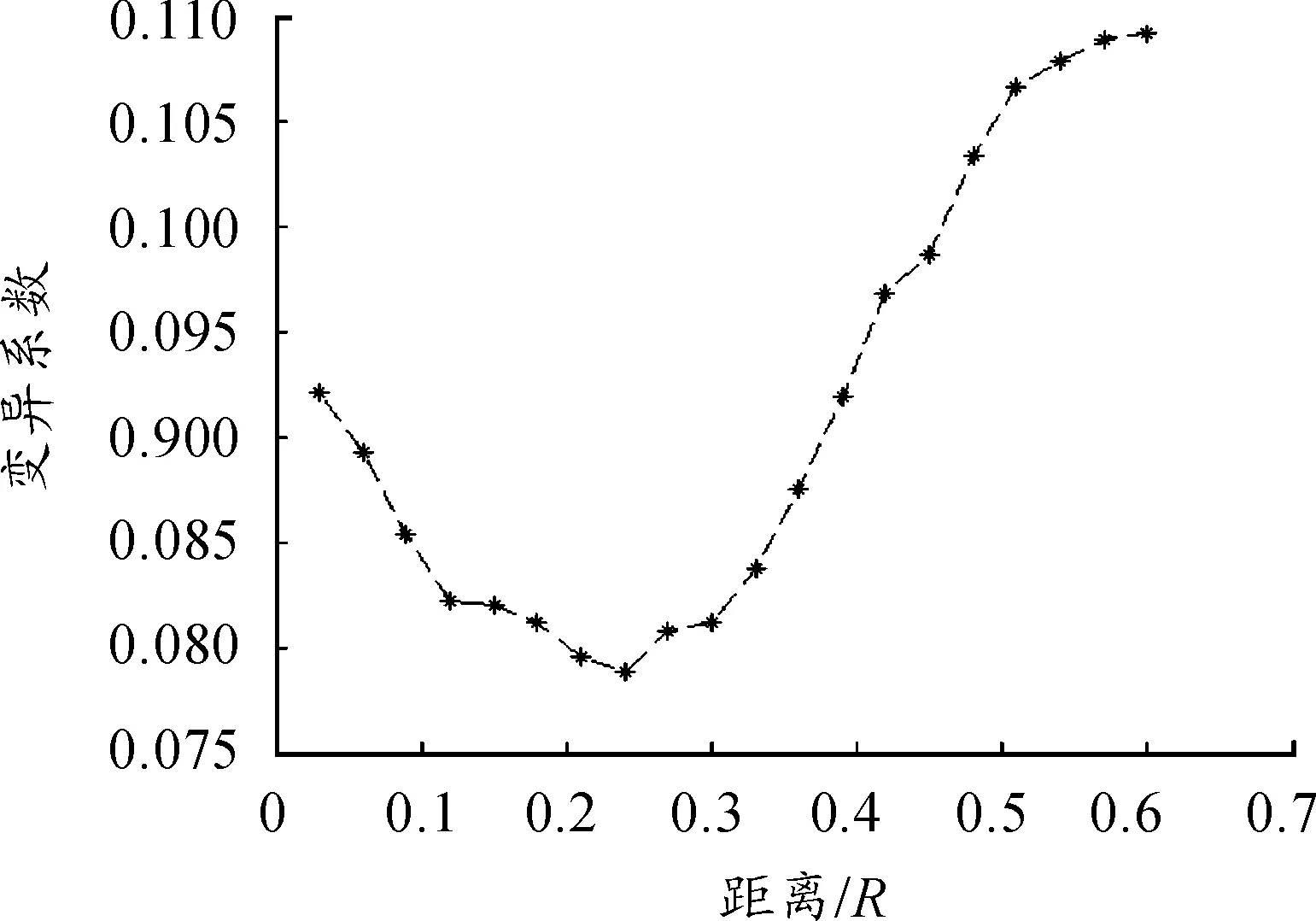
图8 抄板个数的数值实验结果

将每层空间划分为20个空间类，图8的纵值表示对应的kcv值。根据模拟结果可以发现，总共有七个空间类的kcv值大于0.2，而有七个空间类的kcv值在0.1左右。从中可看出，前述的七个空间类主要受到了抄板作用，它们的边缘有另外三个空间类，抄板对该三个空间类的作用比较小。抄板对其他的空间类则没有明显作用。因此，可以判定被抄板作用到的空间大概占17.5%～25.0%。抄板在现实安装时要相互避开，才可使其独立作用而不相互影响。因此抄板的个数在4个或5个时最佳。

5 抄板角度模拟分析

当抄板设置呈一定角度时，可加快颗粒之间的交互作用。抄板的角度为90°时，抄板其中一侧的颗粒难于运动至另一侧，混合效果很差。抄板为0°时，不起到任何作用。根据前述的方法进行模拟，本文选取的抄板角度从45°逐渐增加到90°。根据模拟得到如下表1中的数值结果。由表1的数据绘制成图9。

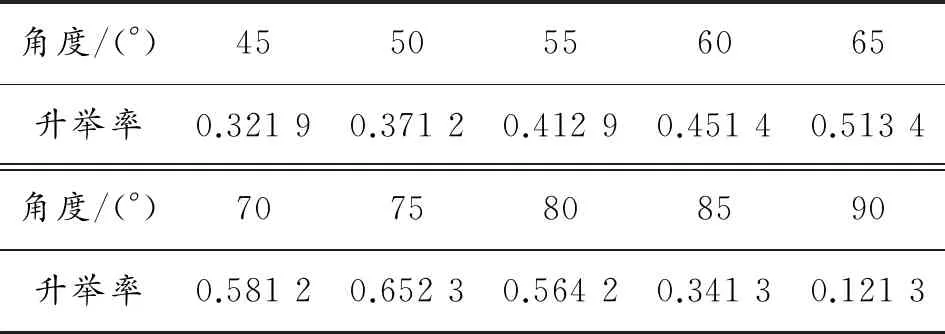
表1 抄板在不同角度下颗粒的升举率

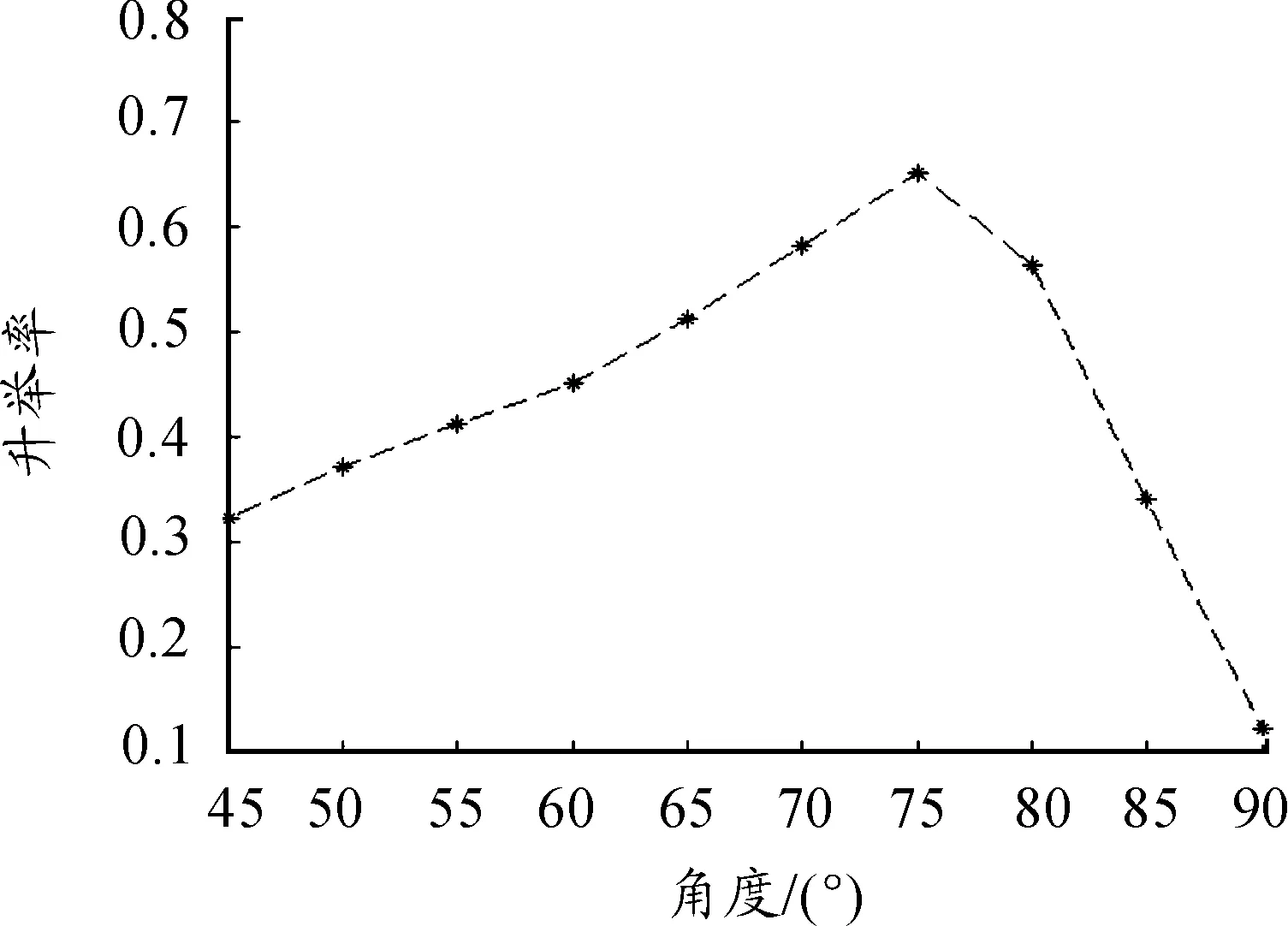
图9 抄板角度的数值实验结果

由图9可以看出，升举率在抄板所呈的角度为90°时达到最低，其值逼近0，即抄板其中一侧的颗粒难于运动至另一侧。角度从45°逐渐变大，升举率也逐渐随之提高，在抄板所呈的角度到达75°时达到最大值。随后随着抄板角度的继续增大，升举率逐渐减小。由图9可知，升举率在抄板所呈的角度为75°最大，也就是说此时的混合效果最好，现实生活中，抄板的角度一般为70°～80°。

6 结论

以EDEM软件对单元空间内的颗粒进行模拟，通过模拟结果讨论混合效果，并对其进行放大，得出了颗粒数的变化情况，并得出如下结论。

1) 抄板长度和旋转筒内半径的比值为0.4时颗粒的混合效果最好。

2) 抄板设置时，其外侧和筒内壁的距离d1与筒内半径r的比值在[0.2,0.25]时，颗粒的混合最佳。

3) 旋转筒内在其装填颗粒的量为40%时，可以达到最佳的颗粒混合效果，所设置的抄板的数量最好为4个～5个。

4) 抄板和筒底面的夹角的最佳值应为75°。

[1] 耿凡，徐大勇，袁竹林，等.滚筒干燥器中颗粒混合运动的三维数值模拟[J].应用力学学报,2008，25(3)：529-534.

[2] LIU P Y， YANG R Y， YU A B.DEM study of the transverse mixing of wet particles in rotating drums[J].Chemical Engineering Science,2013(86)：99-107.

[3] GUI Nan，YAN Jie，XU Wenkai.DEM simulation and analysis of particle mixing and heat conduction in a rotating drum[J].Chemical Engineering Science,2013(97)：225-234.

[4] HÖHER D，WIRTZ S，SCHERER V.A study on the influence of particle shape and shape approximation on particle mechanics in a rotating drum using discrete method[J].Powder Technology,2014，253：256-265.

[5] XU Yong，XU Chunhui，ZHOU Zhe.2D DEM simulation of particle mixing in rotating drum：A parametric study[J].Particuology,2010，8：141-149.

[6] 黄德财，陆明，赵省向.旋转筒内黑索今和铝颗粒混合与分离的计算机模拟[J].计算物理,2011，28(3)：445-450.

[7] HUANG Decai，LU Ming，SU Gang，et al.Ringlike spin segregation of binary mixtures in a high-velocity rotating drum[M].Physical Review E 85.031305,2012.

[8] BAKER C G J.The desige of flights in cascading rotary dryers[M].Drying Technology,1988(4)：100.

[9] VAN PUYVELDE D R.Comparison of discrete elemental modeling to experimental data regarding mixing of solids in the transverse direction of a rotating kiln[J].Chemical Engineering Science,2006,61(13):4462-4465.

[10] KNIGHT J B,JAEGER H M,NAGEL S R.Vibration-induced size separation in granular media:The convection connection[J].Phys Rev Lett,1993,70(24):3728-3731.

[11] DEAN B,MUZZIO F J,Enhanced mixing in double cone blenders[J].Powder Technology,2000,110(2):179-189.

[12] 黄志刚.转筒干燥器直角抄板的模拟与试验研究[J].计算机仿真,2004,21(6)：60-62.

[13] SCHAFER J，DIPPEL S， WOLF D E.Force Schemes in Simulations of Granular Meterials[J].J.Phys.I France,1996,5(20)：5-18.

[14] CHEN Guo-liang.More realistic parallel computational model[J].Mini-Micro Systems,1995,16(2)：1-9.

(责任编辑杨继森)

TheoreticalCalculationfortheInfluenceofMixingEffectofRDX-AlbyCopyBoardUsingDiscreteElementModel

WANG Zhenghong1, LIN Qiuhan2, LI Shiwei1， WANG Cailing3, ZHAO Shengxiang3, LI Jianliang2

(1. Liaoning Qingyang Chemical Industry Corporation, Liaoyang 111002, China; 2.School of Chemical Engineering，Nanjing University of Science and Technology, Nanjing 210094, China; 3.Xi’an Modern Chemistry Research Institute, Xi’an 710065, China)

The discrete element software is used to simulate the particle system in the unit space. Based on the simulation of the particle change in the mixing process of the rotating drum, the effect of the plate on the mixing effect of RDX-Al is studied. The influence of the length of the plate, the angle of setting, the number of addition and the filling rate on the degree of stirring uniformity are investigated, and the optimum parameters are given. The results show that the mixing effect is best when the ratio of the length of the plate to the radius of the rotating cylinder is 0.4 and the distance between the plate and the inner wall of the rotating cylinder is 0.2 of the radius of the rotating cylinder. When the loading amount is 40%, and the added amount of the plate is 4 (or 5), the stirring and mixing effect is best. When the plate setting angle is 75 degrees, the mixing effect is the best. The research conclusions of this paper will provide reference and guidance for the mixing of RDX-Al in the actual industrial production.

discrete element method; particle mixing effect; copy board; grid division

2017-03-20；

：2017-04-15

林秋汉(1985—)，男，博士，主要从事含能材料的合成与应用研究。

10.11809/scbgxb2017.09.036

format:WANG Zhenghong, LIN Qiuhan, LI Shiwei，et al.Theoretical Calculation for the Influence of Mixing Effect of RDX-Al by Copy Board Using Discrete Element Model [J].Journal of Ordnance Equipment Engineering,2017(9):168-172.

O4-39

：A

2096-2304(2017)09-0168-05

本文引用格式：王正宏，林秋汉，李世伟，等.以离散元方法研究抄板对RDX-Al混合效果的影响[J].兵器装备工程学报，2017(9):168-172.