考虑动力刚化的挠性航天器的动力学建模与分析

方 柳，刘玉亮，赵桂平

(1.西安交通大学 航天航空学院，机械结构强度与振动国家重点实验室， 西安 710049； 2.大连理工大学 航空航天学院， 辽宁 大连 116024)

【装备理论与装备技术】

考虑动力刚化的挠性航天器的动力学建模与分析

方 柳1，刘玉亮2，赵桂平1

(1.西安交通大学 航天航空学院，机械结构强度与振动国家重点实验室， 西安 710049； 2.大连理工大学 航空航天学院， 辽宁 大连 116024)

本文以含有挠性太阳能帆板的卫星为研究对象，建立了考虑动力刚化效应的刚柔耦合动力学模型，并与传统的线性模型进行了对比。首先，通过Hamilton变分原理建立了考虑动力刚化效应的挠性卫星的姿态运动和结构振动的偏微分方程；之后，通过假设模态法对偏微分方程进行离散，得到离散化后的线性模型和动力刚化模型；最后，给出了某些特定外界激励下两种模型动力学响应的数值仿真结果。仿真结果表明，动力刚化效应将对卫星的柔性结构振动产生较大影响；在一定的外界激励下，采用线型模型的计算结果与动力刚化模型的计算结果之间存在较大偏差。

刚柔耦合；动力刚化；Hamilton变分原理；假设模态法

随着航天技术的发展，人们对航天器的任务需求也越来越复杂。传统刚体航天器已无法满足人们的需求。为了节约发射成本，现有的航天器大都采用质量轻，刚度小的柔性结构，如柔性太阳帆板，大型柔性天线等可展开结构[1-3]。柔性结构的引入为航天器在轨动力学建模与分析带来了困难。太阳帆板 等柔性部件的结构振动将对航天器的姿态运动产生影响，而航天器的姿态运动又会反过来作用在航天器的柔性部件上，产生刚柔耦合作用。为了充分保证航天器的正常在轨运行，就必须对该类航天器的刚柔耦合机理进行研究。

现有关于柔性航天器的刚柔耦合作用的研究大都没有考虑旋转带来的刚化效应。20世纪七、八十年代，为了解决航天技术中面临的实际工程问题，以Meirovitch[4-6]和Stemple[7-8]为首的学者通过采用Hamilton变分原理，以及小变形假设建立起柔性结构振动理论，并在此基础上演化出目前进行动力学分析和控制系统设计时广泛采用的传统线性模型。传统线性模型通过采用分离变量法对偏微分线性方程进行处理，推导出基于模态坐标法描述结构振动的理论。该类方法具有计算量小，结构形式简单等优点，得到了广泛应用。然而随着传统结构频率的不断降低以及航天器姿态机动速度不断增加，传统的线性模型在计算结构振动时出现了误差不断增加的情况。1987年，Kane[9]在对固结于运动基座上的悬臂梁进行动力学分析时发现，当悬臂梁高速旋转时，按零次近似动力学模型计算出的悬臂梁挠度趋于发散且刚度为零或为负，然而实验得到的结论却与理论分析相反。因此，Kane首次提出了动力刚化的概念，对传统的零次模型进行了修正，提出了与实验结果相符合的动力刚化模型。

自从该概念提出以来，国内、外学者对其进行了广泛的研究，大都在柔性体的变形-应变关系中考虑了非线性项。对非线性项处理的方法大致可分为两类，一类是在柔性体的变形场中加入非线性项使得系统产生动力刚化项[10-11]；其二是在线性化动力学方程中加入由刚体大范围运动所产生的惯性载荷引起的几何动力刚化项[12-13]。章定国等[14-16]以旋转悬臂柔性梁为研究对象，在考虑横向变形引起的纵向缩短的二阶耦合变形量的条件下，用Hamilton变分原理和假设模态法推导出了考虑“动力刚化”的一次近似耦合模型，研究了旋转悬臂柔性梁的频率转向和频率转换特性。杨辉等[17-18]对柔性梁的“动力刚化”现象进行了实验研究，结果表明在某些高速旋转情况下，传统零次近似模型不能够准确计算梁的横向振动响应，而实验得到的梁的横向振动响应与一次近似耦合模型预测的结果一致，验证了一次近似耦合模型的正确性。在上述文献中，大都只对旋转作用下，挠性结构的振动特性进行分析[14-18]，并未深入研究动力刚化作用下结构振动对航天器姿态运动的影响。而且，文献[17-18]所采用的动力学模型为有限元模型。由于有限元模型阶次较高，不适合作为航天器姿态控制系统和振动抑制系统设计的模型。

基于上述问题，本文以美军宽带全球卫星通信系统-1[19](如图1所示)为研究对象，建立了含有动力刚化项的刚柔耦合模型，采用假设模态法进行离散，得到适合作为该卫星姿态控制系统和振动抑制系统设计的模型，对姿态运动和结构振动之间的耦合作用进行了研究。此外，还将与传统的线性模型对比，通过数值仿真验证他们之间的差异。全文安排如下：第一节，采用Hamilton变分原理建立卫星偏微分方程；第二节，通过假设模态法对偏微分方程进行离散，得到离散化的传统线性模型和动力刚化模型；第三节，给出数值仿真算例；在第四节给出结论。

图1 美军宽带全球卫星通信系统-1

1 运动方程

为了使问题简化，本文只考虑卫星在平面内的运动，卫星的姿态运动和结构振动的示意图如图2所示。

图2 卫星姿态运动和结构振动示意图

(1)

质量单元dm的速度可表示为：

(2)

(3)

这里，IC表示中心刚体绕OZo的转动惯量；令dm=σdx，其中，σ表示柔性帆板的单位长度质量，这里假设柔性帆板是均匀的，各向同性的欧拉伯努利梁，因此σ是一个常数。卫星的弹性势能可表示为：

(4)

其中，EI表示梁的抗弯刚度；l表示梁的长度。

(5)

结合式(4)和式(5)，利用Hamilton变分原理，可推出卫星姿态运动和结构振动的偏微分运动方程。Hamilton变分原理可表示为：

(6)

这里，L=T-U表示Lagrange函数；Wτ表示外力所做的虚功，这里的外力只考虑作用在中心刚体的质心O处的力偶τ，满足δWτ=τδθ,这里δθ表示卫星姿态运动的虚位移。由式(6)可导出：

(7)

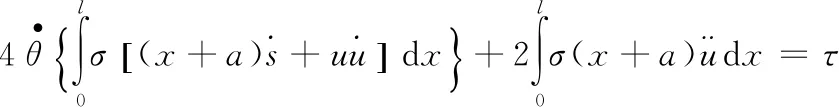
(8)

其边界条件为：

u(0,t)=0

(9.a)

u(1)(0,t)=0

(9.b)

u(2)(l,t)=0

(9.c)

u(3)(l,t)=0

(9.d)

其中，u(i),i=1,2,3,4，表示u相对于x的第i阶导数。

2 模型的离散化

2.1 模态正交性

传统的线性模型是通过对式(7)和式(8)简化得到，其方程为：

(10)

(11)

u(x,t)=φ(x)q(t)=φq

(12)

将其带入式(10)并将φ和q移动至方程的两边，可得：

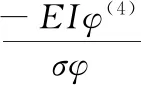
(13)

其中，ω是一个常数，表示梁振动的频率。式(10)的边界条件可以简化为：

φ(0)=0

(14.a)

φ(1)(0)=0

(14.b)

φ(2)(l)=0

(14.c)

φ(3)(l)=0

父母应该引导孩子不要非常强烈地在乎细节上的对和错，因为对错往往是相对的。对于孩子做的事情，父母也不要总用对错来分析。

(14.d)

将式(13)进行处理，可转化为：

EIφ(4)=σφω2

(15)

假设φi和φj分别是梁振动的第i阶和第j阶阵型，ωi和ωj分别是梁振动的第i阶和第j阶频率；将φi带入式(15)，并在两边同时乘以φj积分可得：

(17)

将式(16)展开，结合边界条件(14.a)～ (14.d)可得：

(17)

同理可得：

(18)

将式(17)减去式(18)可得：

(19)

(20)

即方程各模态之间满足正交性。

结合式(15)和边界条件(14.a)～ (14.d)可以求出阵型φ的解析表达式[20]：

φi=A[coshγix-cosγix-

(21)

1+cosγil·coshγil=0

(22)

2.2 线性模型(LM)

设横向变形u可以表示为下式：

u=φTq

(23)

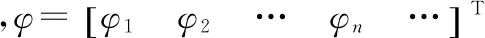
(24)

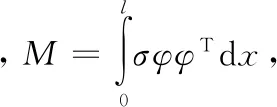
(25)

由式(25)可以看出梁的各阶振动解耦。将式(23)带入式(11)可得：

(26)

2.3 动力刚化模型(DSM)

设横向变形u可以表示为：

u=φTp

(27)

将式(27)带入方程(7)，在方程两边同时乘以φ进行积分，这里φ为归一化的模态；结合正交条件式(19)和式(20)化简可得：

(28)

(29)

将式(27)带入方程(8)进行化简可得：

(30)

式中画横线的部分为线性模型中所忽略的项。

3 仿真算例

本节给出几个数值仿真算例验证模型的有效性。其中，梁的参数值分别为：σ=1 kg/m;l=50 m;a=10 m;EI=6.25×104N·m2;I1=2.15×105kg·m2。 这里只取前两阶模态进行计算ω1=0.351 56 rad/s；ω2=2.203 36 rad/s；F1=256.457 8 kg·m；F2=62.794 9 kg·m；其中Γ=[F1F2]T，D的值为：

(31)

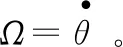
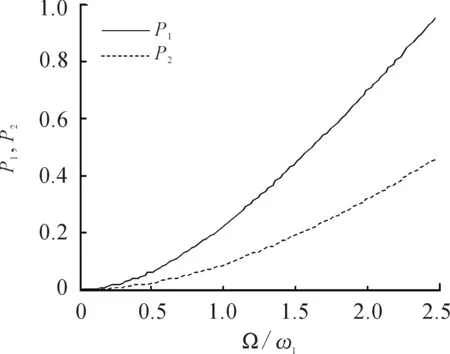
图3 旋转对结构振动角频率的影响

第二个算例是在已知规律旋转角速度下的动力学响应。旋转规律为:

(32)

其中，Ω0=0.5 rad/s；T=100 s；初始条件为：

q1=q2=p1=p2=0 m

(33.a)

(33.b)

柔性帆板末端变形的动态响应如图4所示。从图中可以看出，在卫星的旋转角速度达到某一转速的情况下，采用传统线性模型计算的结果与动力刚化模型的计算结果存在很大偏差。因此，当卫星的挠性附件的结构频率较低时，需采用动力刚化模型进行动力学分析和控制系统的设计，否则将产生较大误差。此外，从图中还可以看出采用动力刚化模型计算得到的结果比传统线性模型的计算结果变形要小，这主要是因为动力刚化效应使柔性梁的等效刚度增加，从而使其不易发生变形，这也从侧面说明了动力刚化模型的有效性。

图4 柔性梁末端随时间响应

为了分析动力刚化模型对卫星姿态控制系统的影响，本文还将给出已知外界一定规律力矩作用在中心刚体上的卫星姿态动力学响应和柔性梁末端变形的动力学响应，力矩的施加规律为：

(34)

其中， τ0=1.075×103N·m；模态的初始条件与式(33.a)和(33.b)相同；卫星的姿态初始条件为：

(35)

图5和图6表示卫星姿态的动力学响应，图6是图5的局部放大；图7表示挠性帆板末端动力学响应。

图5 卫星的姿态角随时间响应

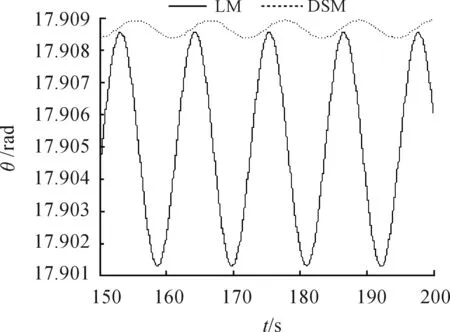
图6 卫星的姿态角随时间响应

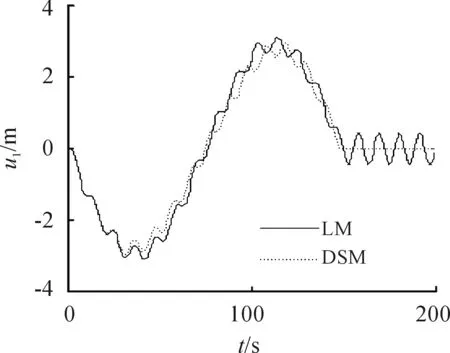
图7 柔性帆板末端变形随时间响应

从图5和图6可以看出，两种模型的姿态运动规律差别很小，说明动力刚化效应对卫星的姿态运动影响很小。这主要是因为挠性帆板的质量占总体质量百分比较小，而卫星的中心刚体质量占主导，使卫星的结构振动并不会对卫星姿态运动产生较大影响。即使动力刚化效应对卫星的结构振动产生较大影响，对姿态运动的影响却很小。然而，动力刚化效应对姿态运动的影响将会随着柔性附件质量与总质量的比值的增加而增加。此外，由图7可以看出，卫星在受到激励的过程中，动力刚化模型的结构形变要小于线性模型。此结果与第二例仿真结果相同。

4 结论

本文以美军宽带全球卫星通信系统-1为研究对象，研究了动力刚化效应对其姿态运动和结构振动的影响。研究结果表明：

1) 对于带有大型挠性帆板且结构角频率较低的卫星，动力刚化现象会对卫星的结构振动产生较大影响，采用传统线性模型的计算结果存在较大误差；

2) 卫星的旋转角速度与柔性结构的一阶角频率的比值越大，动力刚化效应对柔性结构振动的影响越大。对于本文的研究对象，当卫星的旋转角速度为结构一阶角频率的2.5倍时，其结构振动的一阶结构角频率大约增加一倍。

[1] 苗常青,李学涛,马浩.空间充气展开天线支撑结构的模态分析[J].哈尔滨工业大学学报,2005,37(11):1589-1591.

[2] GRAHNE M S,SIMBURGER E J.Inflatable solar arrays[J].Progress in Astronautics and Aeronautics.,2001,191:463-479.

[3] 李洋.柔性航天器在轨振动主动控制研究[D].西安：西安电子科技大学,2013.

[4] MEIROVITCH L.Dynamics and control of structures[M].John Wiley & Sons,1990.

[5] MEIROVITCH L,SILVERBERG L M.Active vibration suppression of a cantilever wing[J].Journal of Sound and Vibration,1984,97(3):489-498.

[6] MEIROVITCH L.A modal analysis for the response of linear gyroscopic systems[J].Journal of Applied Mechanics,1975,42(2):446-450.

[7] CHANDRA R,STEMPLE A D,CHOPRA I.Thin-walled composite beams under bending,torsional,and extensional loads[J].Journal of Aircraft,1990,27(7):619-626.

[8] STEMPLE A D,LEE S W.Finite-element model for composite beams with arbitrary cross-sectional warping[J].AIAA journal,1988,26(12):1512-1520.

[9] KANE T R,RYAN R,BANERJEE A K.Dynamics of a cantilever beam attached to a moving base[J].Journal of Guidance,Control,and Dynamics,1987,10(2):139-151.

[10] WU S C,HAUG E J.Geometric non-linear substructuring for dynamics of flexible mechanical systems[J].International Journal for Numerical Methods in Engineering,1988,26(10):2211-2226.

[11] ZHANG D J,LIU C Q,HUSTON R L.On the dynamics of an arbitrary flexible body with large overall motion:an integrated approach[J].Journal of Structural Mechanics,1995,23(3):419-438.

[12] YOO H H,RYAN R R,SCOTT R A.Dynamics of flexible beams undergoing overall motions[J].Journal of Sound and vibration,1995,181(2):261-278.

[13] YOO H H,SHIN S H.Vibration analysis of rotating cantilever beams[J].Journal of Sound and Vibration,1998,212(5):807-828.

[14] 方建士，章定国．旋转悬臂梁的刚柔耦合动力学建模与频率分析[J].计算力学学报，2012，29(3)：333-339.

[15] 章定国，朱志远．一类刚柔耦合系统的动力刚化分析[J]．南京理工大学学报，2006,30(1)：21-26.

[16] 方建士，黎 亮，章定国等．基于刚柔耦合动力学的旋转悬臂梁的频率转向与振型转换特性[J].机械工程学报，2015，51(17)：59-65.

[17] 杨辉，洪嘉振，余征跃．动力刚化问题的实验研究[J]．力学学报，2004，36(1)：118-124.

[18] 杨辉,洪嘉振,余征跃.刚-柔耦合多体系统动力学建模与数值仿真[J].计算力学学报,2003,20(4):402-408.

[19] 张雷.航天器分步展开式太阳翼设计与研究[D].上海：上海交通大学,2012.

[20] 张亚辉,林家浩.结构动力学基础[M].大连理工大学出版社,2007.[21] LIU Y,WU S,ZHANG K,et al.Parametrical Excitation Model for Rigid-Flexible Coupling System of Solar Power Satellite[J].Journal of Guidance, Control, and Dynamics, 2017.

(责任编辑周江川)

DynamicModelingandAnalysisforFlexibleSpacecraftwithDynamicStiffening

FANG Liu1, LIU Yuliang2, ZHAO Gui-ping1

(1.State key Laboratory for Strength and Vibration of Mechanical Structure, School of Aerospace， Xi’an Jiaotong University School of Aerospace, Xi’an 710049, China; 2.School of Aeronautics and Astronautics， Dalian University of Technology， Dalian 116024， China)

A satellite with flexible solar panels is studied in this paper. The rigid-flexible coupling dynamic model considering stiffening effect is proposed and compared with the traditional linear model. The partial differential equations of the attitude motion and structural vibration of the flexible satellite with considering stiffening effect are firstly derived from Hamilton’s principle. Then the linear model and the dynamic stiffening model are obtained by discretizing the partial differential equations using assumption mode method. At last, numerical simulations of the dynamic responses of the two models under certain external excitation are presented. The results show that stiffening effect has a significant influence on the flexible structure vibration, and there will be a lot of deviation between the results computed by the linear model and dynamic model under a certain external excitation.

rigid-flexible; dynamic stiffening; Hamilton’s law of variation principle; assumption mode method

2017-04-10；

：2017-04-30

：国家自然科学基金项目(11372237)

方柳(1990—)，女，硕士研究生，主要从事工程力学研究；刘玉亮(1991—)，男，博士研究生，主要从事大型空间结构的姿态动力学、轨道动力学与控制研究。

赵桂平(1958—)，女，博士，教授，主要从事工程力学研究。

10.11809/scbgxb2017.09.014

format:FANG Liu, LIU Yuliang,ZHAO Gui-ping.Dynamic Modeling and Analysis for Flexible Spacecraft with Dynamic Stiffening[J].Journal of Ordnance Equipment Engineering,2017(9):67-72.

V411.4

：A

2096-2304(2017)09-0067-06

本文引用格式：方柳，刘玉亮，赵桂平.考虑动力刚化的挠性航天器的动力学建模与分析[J].兵器装备工程学报，2017(9):67-72.