考虑钻具屈曲的环空流动仿真研究

袁兰峰，何世明，黎学年，汤明，邵庸

（1.西南石油大学油气藏地质及开发工程国家重点实验室，四川 成都 610050；2.中国石化华东石油工程公司钻井处，江苏 南京 210000）

考虑钻具屈曲的环空流动仿真研究

袁兰峰1，何世明1，黎学年2，汤明1，邵庸1

（1.西南石油大学油气藏地质及开发工程国家重点实验室，四川 成都 610050；2.中国石化华东石油工程公司钻井处，江苏 南京 210000）

在小井眼定向井和水平井钻井过程中，钻具屈曲会对环空流场、压力场产生较大影响。文中借助流体动力学计算软件ANSYS FLUENT开展了考虑钻具正弦、螺旋屈曲的环空流动仿真模拟，系统地研究了不同环空偏心距、不同转速等因素对环空流场和流动压降的影响规律。研究发现：同心环空中，流体流速沿径向对称分布，偏心、屈曲环空中偏离对称分布；环空间隙越大，环空流速就越大；当考虑钻柱旋转时，钻柱旋转对环空窄间隙处流速的影响比对环空宽间隙处的影响要大，可明显提高环空窄间隙处的流速；同心环空、偏心环空压降值沿井深呈线性增加，偏心度越大，压降越小；屈曲环空压降值沿井深呈非线性增加，转速越大，压降越小。仿真结果与实验结果相比，具有较高的准确性，对真实钻井条件下环空压降的计算具有一定的指导意义。

偏心环空；正弦屈曲；螺旋屈曲；压降；ANSYS FLUENT软件

0 引言

随着油气开采向着深部地层及深水方向发展，钻遇窄安全密度窗口地层的情况越来越普遍，环空压降的预测不准常会造成井漏、井喷等安全事故，环空结构作为影响环空压降的一个重要因素，引起了重点关注。

流体在环空中的流动相较于在直管中要复杂得多，早期的油田实践和室内实验对流体在环空中的流动规律已经作了许多研究，其中对牛顿流体［1-2］、非牛顿流体［3-6］在层流、紊流流态下的流动规律主要是应用实验、理论解析以及数值分析方法进行了求解，并得到了许多有价值的结论。但这些研究主要是以同心、偏心环空结构为主，对屈曲环空中的速度场、压力场分布规律研究较少，然而在实际钻井过程中，所钻井多为大斜度井或水平井，钻柱由于受到重力的作用总是靠向环空低边发生偏心现象，同时当钻柱轴向载荷超过其临界屈曲载荷时就会发生弯曲［7］，所以，实际环空多为偏心与屈曲环空相结合，而非单一的同心或偏心结构。因此，传统的水力学模型并不能完全、准确预测实际钻井条件下的压降。

现阶段国内外关于内管旋转条件下屈曲环空流场、压力场研究较少，为此，本文基于CFD仿真实验，对考虑内管旋转条件下的屈曲环空流场和压力场进行了数值模拟研究，得出了不同偏心距、不同转速时的流场和压力场的变化规律。

1 研究问题及模型

1.1 屈曲环空的形成

在定向井及水平井的钻井过程中，由于钻柱受到轴向压力作用，一旦轴向载荷超过发生屈曲的临界载荷，钻柱就会发生屈曲。确定钻柱发生螺旋屈曲时的临界载荷方程为

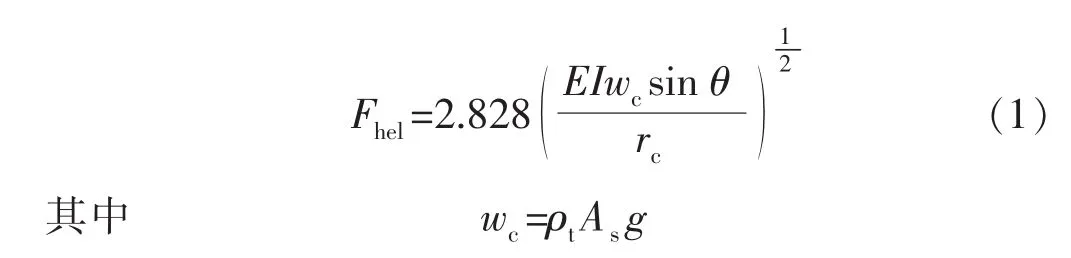
式中：Fhel为螺旋屈曲临界载荷，N；E为弹性模量，Pa；I为转动惯量，kg·m2；wc为定义常数；rc为钻柱与井眼间的间距，m；θ为井斜角，（°）；ρt为管材的单位长度的质量，kg/m；As为管柱的横截面积，m2；g为重力加速度，m/s2。

Miska等［8-9］提出了在水平井段钻柱发生正弦屈曲时的临界载荷方程：

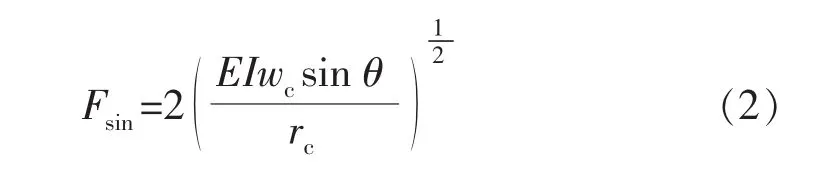
式中：Fsin为正弦屈曲临界载荷，N。

钻柱在轴向压力超过其临界载荷时，会发生正弦屈曲或螺旋屈曲，此时，由屈曲钻柱与井壁或套管壁形成的环空称之为屈曲环空，研究钻柱屈曲条件下的环空压力更切合实际情况。

1.2 CFD仿真模型及输入参数

1.2.1 控制方程及边界条件

对于不可压缩、等温且处于层流流态下的流体来说，其有效黏度仅仅与应变率张量有关。液体流动模型可使用圆柱坐标系下的连续性方程以及轴向、径向、周向方向的动量方程进行描述。

仿真时的边界条件包括速度入口、流量出口及固体壁面等。其中：入口轴向速度u设定为0.83 m/s，径向速度v和切向速度w均为0；当钻柱旋转时，在井壁处u=v=w=0，在钻柱壁面处，u=w=0，v=wRi。Ri为钻杆外径。

1.2.2 网格划分及物理模型的建立

为了研究非牛顿流体在不同环空结构下的流场、压力场特性，选取10 m长的环空井段，井径为0.1524 m，钻杆外径为0.0889 m，环空结构分为同心、偏心（偏心度分别为0.50，0.93）、屈曲环空（螺旋屈曲、正弦屈曲，其屈曲间距皆为5 m）3种。其中屈曲环空结构如图1所示，用ANSYS-Workbench中自带的mesh模块对网格进行划分。钻井液流体设定为屈服幂律流体，其流变方程为

式（3）中：n为流性指数，本次实验中为 0.416；K为稠度系数，0.591 Pa·sn；τ0为屈服压力，0.846 Pa；ρ为密度，1240 kg/m3。

图1 正弦屈曲几何模型及网格划分

采用基于交错网格的SIMPLE法对连续性方程和N-S方程进行离散化。对动量方程的对流项进行离散化处理时，为保证计算精度，采用二阶格式［10］，设置速度入口边界（0.83 m/s）、流量出口边界、壁面边界（其中环空外壁面始终静止，环空内壁面可旋转，转速为40，60，80 r/min）3类边界类型。为了计算准确，对靠近壁面处网格进行加密处理，坐标系为柱坐标系，速度入口采用速度分量方式，旋转壁面边界为无滑移壁面。

2 仿真结果与讨论

2.1 内管不旋转时径向流速分布

对于同心与偏心环空，取距入口5.00 m处的横截面进行流场分布分析，对于正弦屈曲环空结构，因其不同截面处的流速分布各不相同；故分别取距入口2.50，3.75，5.00 m的3个截面（即管柱分别位于环空高边、环空中央、环空低边时的3个截面）进行流速分布规律分析。同理，对于螺旋屈曲环空结构，分别取距入口0.50，5.00，9.50 m的3个截面 （因管柱发生螺旋屈曲时始终与井壁接触，故所取截面均为偏心环空截面）进行流速分布规律分析。钻柱静止时不同环空结构下流场分布如图2—4所示。

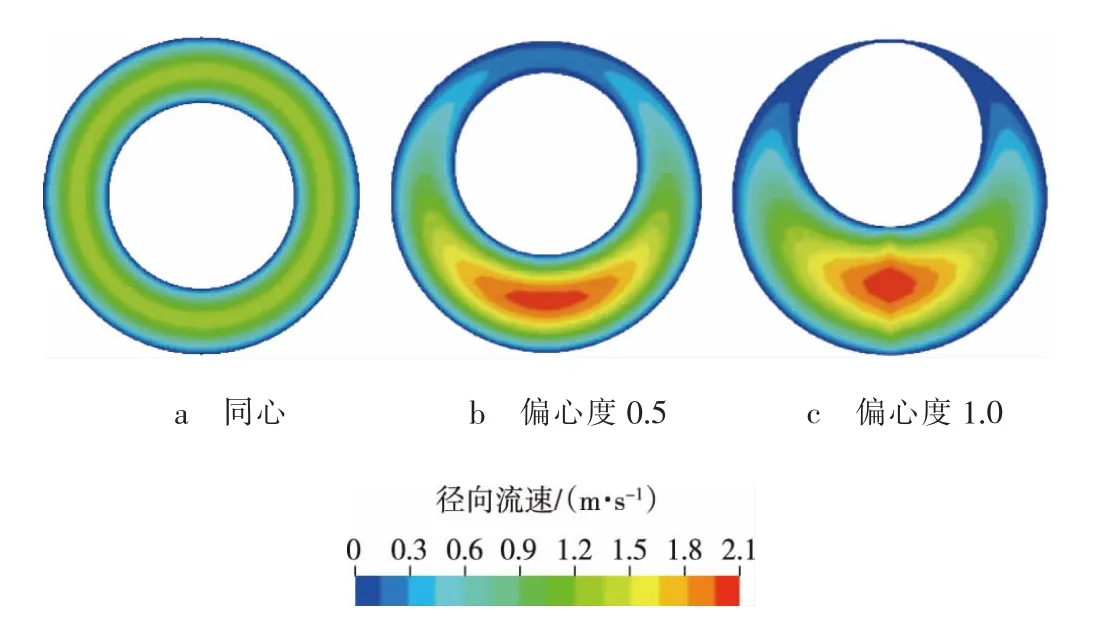
图2 钻柱静止、管柱未发生屈曲时不同环空结构速度云图

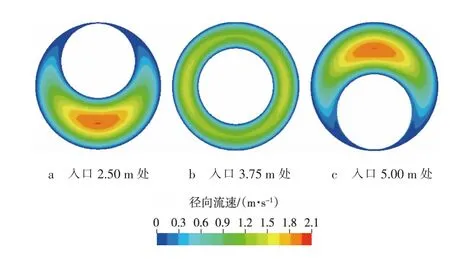
图3 钻柱静止、管柱发生正弦屈曲时环空结构速度云图

由图2可知：在同心环空中，流速沿径向对称分布，最大流速位于环空中心区域，离壁面越近，流速越小。这是因为：靠近壁面时，流体要受到壁面摩擦力的作用，从而产生速度梯度；偏心环空时，流速偏离对称分布，且偏心度越大，偏离越明显，随着偏心度的增加，窄环空间隙处速度减小，宽环空间隙处速度增大，这是由于流体在窄环空间隙处的流动受到了限制，进而大量流向宽环空间隙处的结果。对于定向井及水平井，窄环空间隙处的低流速可能会造成岩屑颗粒的沉积，最终导致岩屑床的形成。

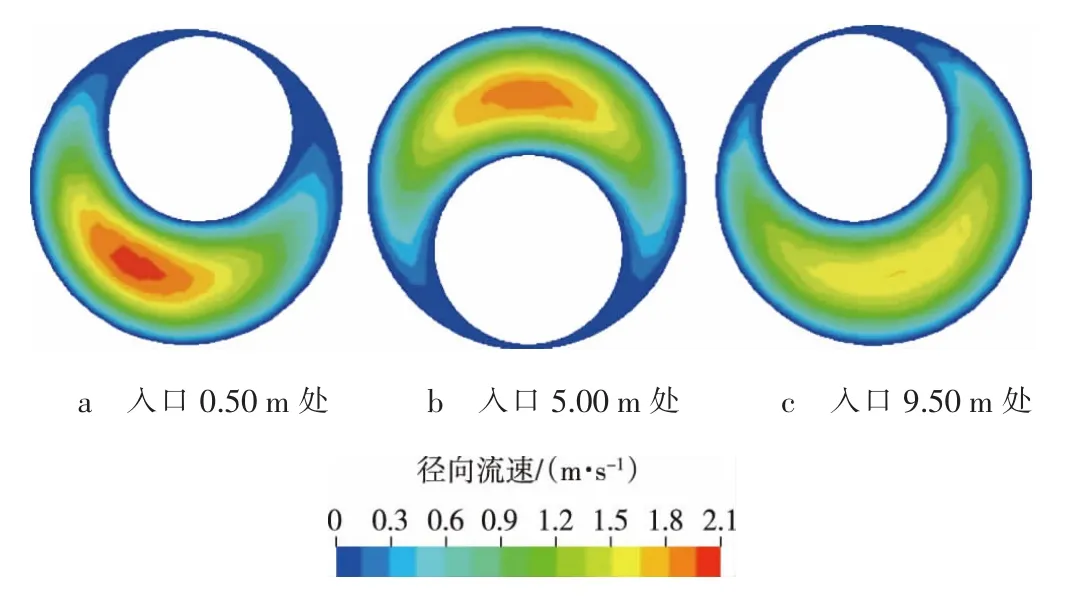
图4 钻柱静止、管柱发生螺旋屈曲时环空结构速度云图

由图3可知，正弦屈曲环空是一个偏心度不断变化的环空结构，在一个屈曲间距内，其环空经历了偏心—同心—偏心的变化过程，环空中流速偏离对称分布，环空间隙越大，流速越大。

图4为螺旋屈曲环空结构速度云图。由图可知，螺旋屈曲环空窄间隙处存在一个流动静止区，在该区域轴向流速接近为0。这与完全偏心环空时观察到的情况一致，最大流速出现在环空间隙最大处，螺旋环空中管柱屈曲位置在不停地变化，相应的，其最大流速区与流动静止区也在不停变化。这将极大地影响流体在环空中的流动，使得流体在环空中流动时产生更多的压耗，故其最大流速区流速呈现逐渐减小的趋势。

2.2 内管旋转时径向流速分布

图5—7为钻柱旋转（转速为40 r/min）时不同环空结构下径向流速分布（因转速为60，80 r/min时的流场分布规律与40 r/min时基本一致，这里不再给出）。将图5—7分别与图2—4进行对比可知，钻柱旋转对同心环空流场分布影响很小，几乎可忽略不计，对偏心、屈曲环空结构窄间隙处的流速却有较大的影响，转速越大，窄环空间隙处的流速越大。这是由于屈服幂律流体具有剪切稀释性，钻柱旋转使流体黏度减小，相应的壁面剪切力减小，故钻柱旋转有利于增大窄环空间隙处的流速。

图8为钻柱静止时，不同环空结构下的压降分布。从图中可以看出：同心、偏心环空结构下的压降随井深的增加呈线性增大的趋势，且偏心度越大，压降越小，即偏心度与压降成反比；模拟正弦屈曲环空压降居于偏心度为0.5与完全偏心时的压降之间，沿井深呈非线性增加，这是因为正弦屈曲环空时其等效偏心度一直在0.5～1.0不断变化的原因；螺旋屈曲环空结构下的压降在0～5.0 m的井深范围内要低于完全偏心环空结构下的压降值，5.0～10.0 m后，其压降值大于完全偏心环空下的压降值，这是因为钻柱屈曲产生额外压耗的缘故，在所讨论的10 m井深范围内，螺旋屈曲环空与同心环空压降值最大达到6 kPa，且随着井深的增加，其压降值还会继续增大。

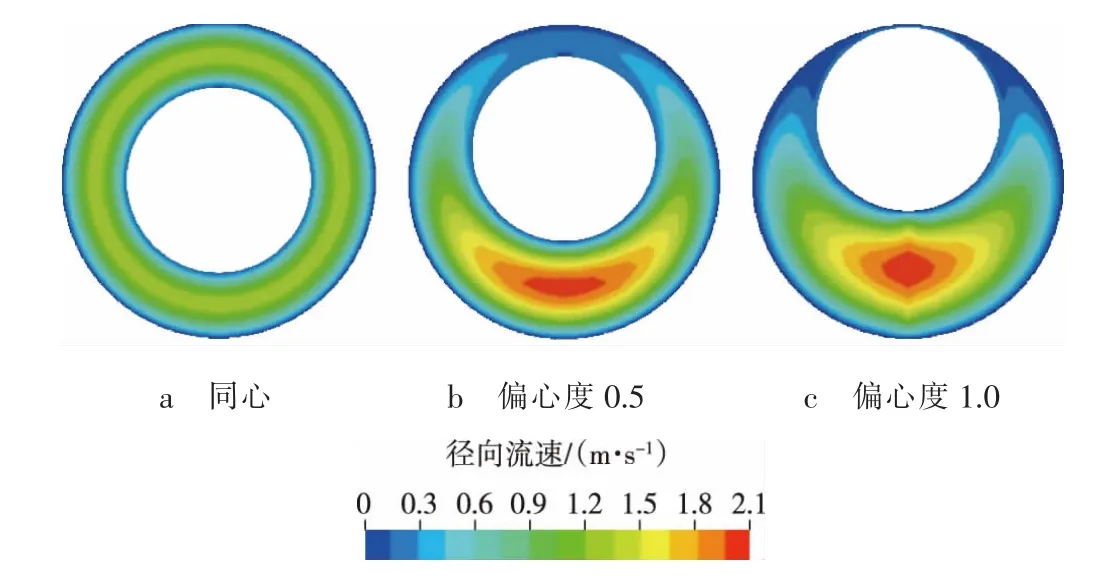
图5 钻柱旋转、管柱未发生屈曲时不同环空结构速度云图

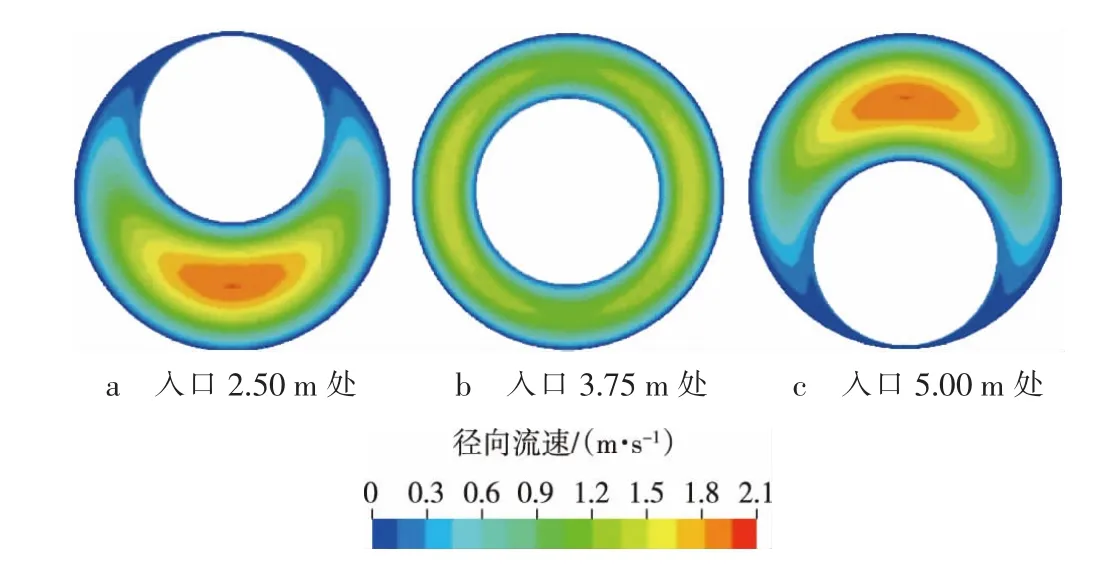
图6 钻柱旋转、管柱发生正弦屈曲时环空结构速度云图

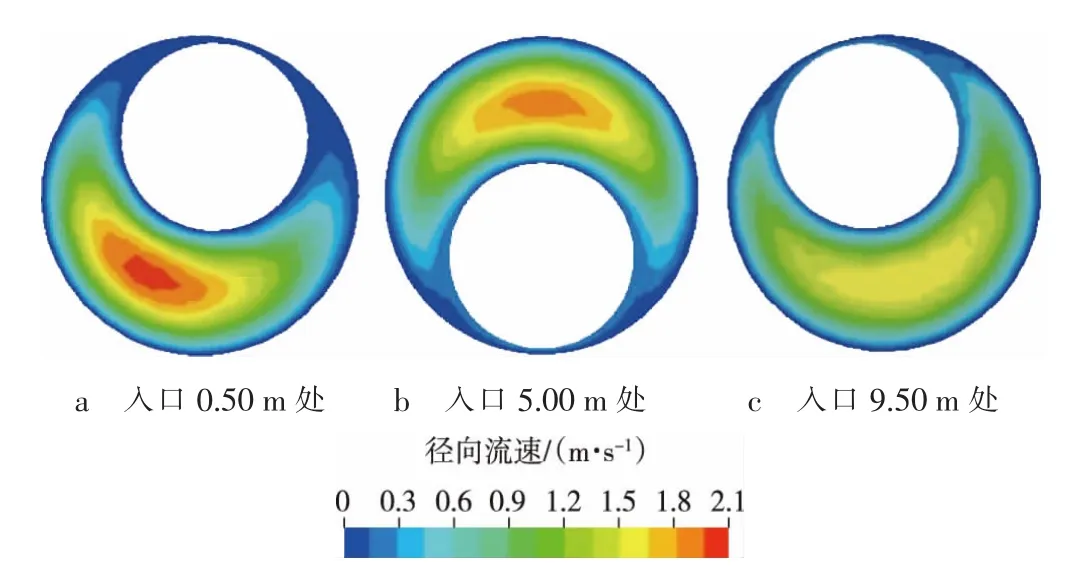
图7 钻柱旋转、管柱发生螺旋屈曲时环空结构速度云图

图8 钻柱静止时不同环空结构下的压降分布

3 仿真结果验证与应用

由于现阶段关于屈曲环空压降的室内实验以及现场数据几乎没有，为了验证CFD仿真试验的准确性，应用汤明在俄克拉荷马大学所获得的关于同心、偏心环空结构下压降的实验测量数据［11］与CFD仿真结果进行了对比，如图9所示。仿真结果与实验结果吻合度较高，同理，用CFD仿真屈曲环空结构下的压降也具有一定的准确性。

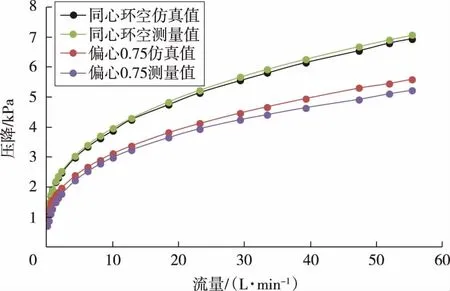
图9 仿真结果与实验结果对比

钻井过程中，钻柱发生正弦屈曲时，偏心率会发生周期性变化，如果以同心环空来计算环空压降，则压降过大；如果以完全偏心环空计算，则压降过小。为了避免因压降计算过大或者过小而引起深部地层的井喷、井漏等安全问题，必须准确计算钻柱发生正弦屈曲时的压降值。此时可将正弦屈曲环空与同心环空压降比和偏心环空与同心环空压降比相结合，利用Tang等［12］关于偏心环空与同心环空压降比拟合式（3）与本文的仿真压降数据相结合，将正弦屈曲环空近似等效为某一偏心度条件下的偏心环空（偏心度恒定）进行处理，从而找到一个适合正弦屈曲的偏心率，以达到真实条件下环空压降的精确计算。

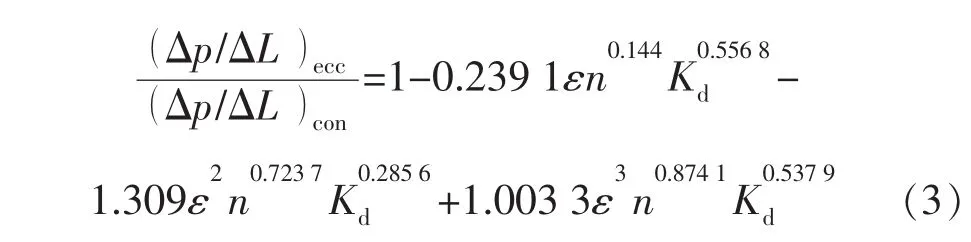
4 结论

1）同心环空中，流体流速沿径向对称分布，偏心、屈曲环空中偏离对称分布，最大流速出现在环空间隙最大处，最小流速出现在环空间隙最小处；钻柱旋转对同心环空流速的影响不大，转速越大，偏心、屈曲环空窄间隙处流速越大，有利于钻井过程中岩屑的运移。

2）同心环空、偏心环空压降值沿井深线性增加，偏心度越大，压降值越小；屈曲环空压降值沿井深非线性增加，随钻柱旋转速度增加，环空压降减小。

3）CFD仿真结果与实验结果相对比，具有较高的准确性，将正弦屈曲环空等效为压降相等的偏心环空近似处理，可以更方便的计算环空压降。

4）屈曲环空结构下的压降变化趋势与常规的同心、偏心结构有所不同，其压降值沿井深方向呈非线性增加，发生周期性变化，考虑到钻遇窄安全密度窗口地层时易引起的井喷、井漏等井下安全问题，精确计算屈曲环空结构下的压降值十分重要，本文为真实钻井条件下环空压降的计算提供了一定的指导。

［1］REDBERGER P J，CHARLES M E.Axial laminar flow in a circular pipe containing a fixed eccentric core［J］.The Canadian Journal of Chemical Engineering，1962，40（4）：148-151.

［2］HEYDA J F.A green′s function solution for the case of laminar incompressible flow between non-concentric circular cylinders［J］. Journal of the Franklin Institute，1959，267（1）：25-34.

［3］钟鑫，孔庆祥.卡森流体轴向同心环空流动规律研究［J］.石油钻采工艺，1987，9（5）：27-36

［4］刘永建，陈家琅.偏心环空中幂律流体轴向层流压降的计算［J］.石油钻采工艺，1989，2（5）：9-15.

［5］VIEIRA NETOJ L，MARTINS A L，ATAIDE C H，et al.The effect of the inner cylinder rotation on the fluid dynamics of non-Newtonian fluids in concentric and eccentric annuli［J］.Brazilian Journal of Chemical Engineering，2014，31（4）：829-838.

［6］张景富，李邦达.幂律液体偏心环空螺旋流层流压降计算［J］.石油钻采工艺，1992，5（5）：13-29.

［7］高德利.油气井管柱力学与工程［M］.东营：中国石油大学出版社，2006：35-38.

［8］MISKA S，CUNHA J C S.Helical buckling of long weightless strings subjected to axial and torsional loads［C］.New York：American Society of Mechanical Engineers，1995.

［9］MISKA S，QIU W，VOLK L，et al.An improved analysis of Axial Force along coiled tubing in inclined/horizontal wellbores［R］.SPE 37056，1996.

［10］张晋凯，李根生，刘广军，等.旋转钻柱内赫巴流体流动模型与流场特性研究［J］.石油机械，2013，41（5）：15-18.

［11］汤明.波动压力与裂缝性地层极限水平段长度研究［D］.成都：西南石油大学，2016.

［12］TANG M，AHAMED R，SRIVASTAV R，et al.Simplified surge pressure model for yield power law fluid in eccentric annuli［J］. Journal of Petroleum Science&Engineering，2016，145（38）：346-356.

（编辑 孙薇）

Simulation of annular flow considering buckling drilling tools

YUAN Lanfeng1,HE Shiming1,LI Xuenian2,TANG Ming1,SHAO Yong1
(1.State Key Laboratory of Oil and Gas Reservoir Geology and Exploitation,Southwest Petroleum University,Chengdu 610050, China;2.Drilling Department,Huadong Petroleum Engineering Company,SINOPEC,Nanjing 210000,China)

During the process of slim-hole directional well and horizontal well drilling,the buckling of drilling tools can affect not only the mechanical properties of the drilling tool assembly,but also the annulus flow field and pressure field greatly.In this paper, the simulations of annular flow about the sinusoidal and helical buckling were carried out by ANSYS Fluent software,and the effects of different annular eccentricity and rotational speed on annular flow velocity field and flow pressure drop were studied systematically.The results show that the flow velocity is distributed symmetrically in the radial direction in the concentric annulus, however,the flow velocity distribution is deviated from the radial direction in the eccentric and buckling annulus;without considering rotation,the larger the annular clearance is,the higher the velocity is;the influence of drill string rotation on the flow velocity at the narrow gap is larger than that at the wide gap;the concentric annulus and eccentric annulus pressure drops increase linearly along the depth of the well,and the larger the eccentricity is,the smaller the pressure drop is;as the depth of well increases,the pressure drop of buckled annulus will also increase nonlinearly,the faster the speed of pipe rotation is,the smaller the pressure drop will be. The simulation results agree well with the experimental results,which has some guidance to the calculation of annular pressure drop under real drilling conditions.

eccentric annulus;sinusoidal buckling;helical buckling;pressure drop;ANSYS FLUENT software

TE347

A

国家自然科学基金项目“基于流-固-化耦合理论的欠平衡钻水平井井壁失稳机理研究”（51474186）、“基于多场耦合理论的页岩气水平井井壁失稳机理研究”（51574202）；国家科技重大专项专题“欠平衡钻井工艺技术研究”（2008ZX05045-03-07HZ）、“特殊结构井井眼稳定及摩阻控制技术”（2011ZX05045-03-01WX）

10.6056/dkyqt201705026

2017-02-20；改回日期：2017-06-22。

袁兰峰，男，1992年生，主要从事油气井流体力学与井控相关研究。E-mail：yuanlanfeng2015@sina.com。

何世明，男，1966年生，教授，博士生导师，主要从事油气井工程力学（井壁稳定、井控与欠平衡钻井）和钻完井新技术等方面的研究及教学工作。E-mail：hesming@sina.com。

袁兰峰，何世明，黎学年,等.考虑钻具屈曲的环空流动仿真研究［J］.断块油气田，2017，24（5）：714-718.

YUAN Lanfeng，HE Shiming，LI Xuenian，et al.Simulation of annular flow considering buckling drilling tools［J］.Fault-Block Oil&Gas Field，2017，24（5）：714-718.