基于前馈解耦的永磁同步电机控制系统研究

，，，，

(1.新疆大学电气工程学院 教育部可再生能源发电与并网控制工程技术研究中心，新疆 乌鲁木齐 830046； 2.金风科技股份有限公司，新疆 乌鲁木齐 830026)

基于前馈解耦的永磁同步电机控制系统研究

荆世博1，王维庆1，王海云1，吴先友2，蒋中川2

(1.新疆大学电气工程学院 教育部可再生能源发电与并网控制工程技术研究中心，新疆 乌鲁木齐 830046； 2.金风科技股份有限公司，新疆 乌鲁木齐 830026)

由于永磁同步电机(PMSM)的前馈解耦采用双闭环的控制器，其全系统的传递函数已高于二阶，导致了控制器参数整定困难。通过分析PMSM以及其解耦控制的速度环和电流环的数学模型，提出了双闭环控制器中被控制量与PMSM数学模型之间的联系，构造出了基于拉氏变换的全系统简化模型，为双闭环控制器的PI参数整定提供了理论依据。针对已构建的全系统传递函数模型的高阶特性，提出了根据劳斯稳定判据来整定PI参数的方法，并在Simulink中进行了实验仿真。仿真结果表明，整定后的参数能够使系统快速趋于稳定，并且具有较好的鲁棒性。

永磁同步电机(PMSM)；前馈解耦；简化模型；劳斯稳定判据

0 引 言

PMSM由于其可靠性高、体积小、控制简单等优点，已经取得了广泛的应用[1]。在PMSM的控制中多采用矢量或直接转矩的控制策略，由于直接转矩的控制方法存在转矩脉动和调速范围窄的问题，在现用的交流伺服系统中一般采用矢量控制[2-3]。

矢量控制一般由电流内环和转速外环构成，其控制策略是利用解耦控制得到近似线性化的模型。矢量控制有多种实现方法，如电流反馈控制、电压前馈控制等[4-6]。考虑到电流反馈控制策略实现方便，控制简单，在电机的控制中一般采用较多[7-8]。在电流反馈控制策略中，电流的控制精度直接影响到转矩控制的精确性和快速性，在实际的电机控制策略中多采用传统的PI控制器来进行电流环和速度环控制。在PI控制器的参数整定中，其整定方法多是依据经验得出，需要反复的试凑。

下面依据PMSM的数学模型与前馈解耦控制器的简化模型，得到PMSM与电流内环和速度外环的传递函数。根据劳斯稳定判据，提出了控制器PI参数整定的方法。仿真表明，根据劳斯稳定判据得到的控制器参数有快速的响应特性，对于系统输入扭矩的波动有较好的鲁棒性，并且能够在较短的时间内使系统趋于稳定。

1 PMSM的数学模型

为便于分析,假设：

1) 转子上的永磁体产生主磁场，转子上无阻尼绕组；

2)忽略齿槽、换相过程和电枢反应等的影响；

3)电枢绕组在定子内表面均匀连续分布；

4)磁路不饱和, 不计涡流和磁滞损耗。

PMSM采用三相星形连接，且没有中线，可得永磁同步电机在d、q轴坐标系下的电压方程与转速方程为[9-10]

(1)

式中:R为电机的等效电阻；ω为转子机械角速度；p为磁极对数；Tm为电机的机械扭矩；F为摩擦系数；Te为电机的电磁扭矩；J为转子的惯性系数；λ为永磁体磁链；id、ud为d轴的电流和电压；iq、uq为q轴的电流和电压；Ld、Lq为直轴和交轴电感，采用表面贴装式电机，Ld=Lq。

2 PMSG传统控制器设计

传统的PMSG的控制策略采用PI控制器对电机测量反馈的d、q轴电流进行对立的调节。为了便于分析，假设电压型逆变器(VSI)没有延迟现象，即VSI所等效一阶惯性传递函数的时间常数为0。传统PMSG及控制的拓扑图如图1所示。

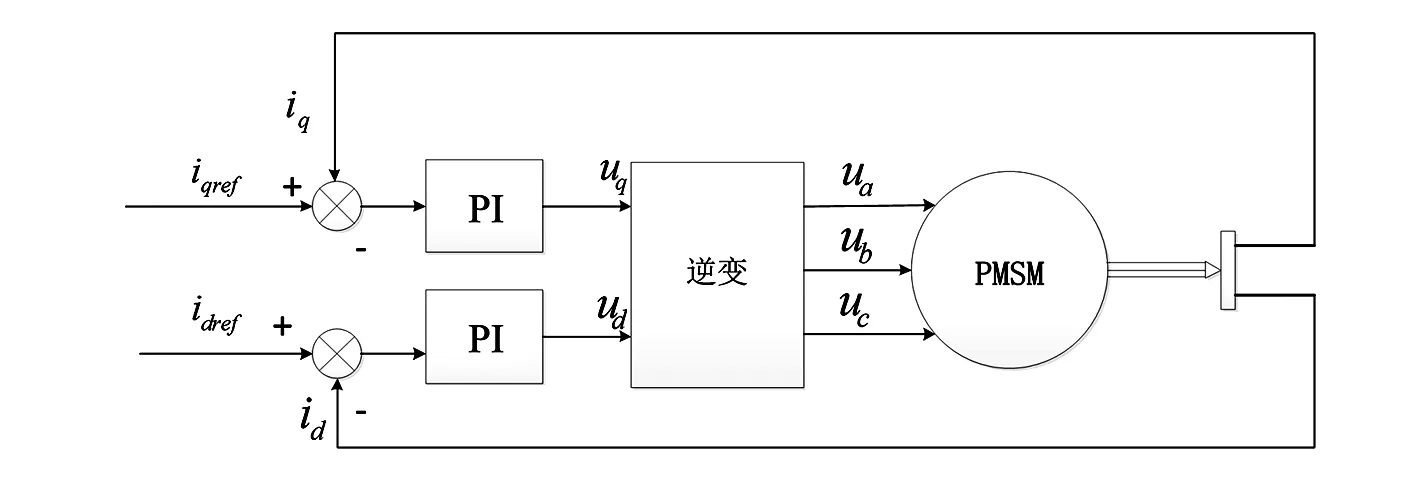
图1 传统PMSG控制策略

在图1的逆变环节中，采用滞环控制生成ua、ub、uc。以q轴为例进行分析，建立q轴等效框图如图2所示。

忽略逆变器的延迟效应，列写如图2所示的传统PMSG的控制策略的开环传递函数：

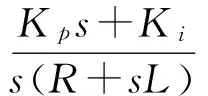
(2)

由以上分析可知，传统PMSG控制系统的开环

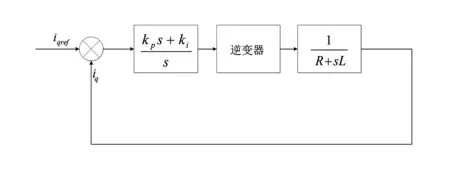
图2 传统PMSG等效控制框图

传递函数为二阶。关于阻尼比ξ：当取临界阻尼时，系统具有最理想的响应时间，且响应速度也最快，但在稳定后，将出现等幅震荡；当阻尼比为过阻尼时，系统将不会出现超调量，并能够最终稳定在设定值，但过阻尼没有超调量是以牺牲调节时间为代价，因此其调节时间较长；欠阻尼的各种情况介于两者之间。综合临界阻尼、过阻尼和欠阻尼的情况，考虑到阻尼比越小，系统的超调量也就越大，但相应的调节时间也就越短，一般取0.4～0.8，这里ξ取0.707。系统的截止频率定为1 000 π。

传统的电流控制器结构简单并且方便建立系统的模型，但忽略了PMSG本体作为控制对象，其a、b、c三相电流经3s/2r变换后，d轴和q轴电流之间的强耦合关系，造成系统的调节时间较长。单纯地依靠PI控制器的调节作用对电机进行控制，往往不能满足控制性能的要求。

3 基于前馈解耦的永磁同步电机PI控制器的设计

3.1 PMSM前馈解耦补偿型电流控制的模型

从式(1)中，可以看出电流的d轴和q轴的电流分量之间存在相互耦合，增加了控制器的设计难度。传统的PI控制器虽然结构简单，控制方便，但其忽略了d轴分量与q轴分量之间的交叉耦合。通过对式(1)中电流分量耦合项的补偿，可以提高控制器的动态性能和控制精度。d轴、q轴耦合项补偿项如式(2)所示。

(2)

基于前馈解耦补偿的PMSM控制系统通常采用电流内环与转速外环的控制结构。在转速外环中，电机的机械转速通过速度传感器进行测量并与参考转速ωref进行比较，产生转速偏差信号，此偏差信号经速度外环的PI控制器调节后作为q轴电流分量的参考值iqref。给定d轴电流分量的参考值idref≡0。将得到的d轴与q轴的电流参考信号与电机定子的三相电流实时测量值经3s/2r变换后的id、iq进行比较，得出d轴、q轴电流分量的偏差值。此偏差值经前馈解耦控制器调节后生成直轴和交轴的电压信号Ud、Uq。将其进行2r/3s变换产生PWM控制信号并送入到三相逆变器中，控制三相逆变器的开关状态，进而控制PMSM输出的三相电压与电流。

由以上分析可得前馈解耦补偿控制策略如图3所示。

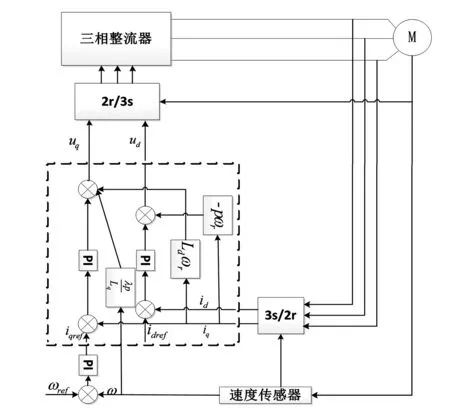
图3 前馈解耦补偿控制策略

3.2前馈解耦控制器的设计

采用d轴电流分量idref≡0的控制方式。将式(3)带入式(1)，可得d轴与q轴的电压方程为

(4)

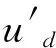
由于Ld=Lq，式(1)的PMSM扭矩方程可表示为

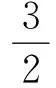
(5)

将式(5)带入式(1)中，可得转速ω与q轴电流分量iq的关系式为

(6)

根据以上的分析，可得q轴电流的传递函数框图如图4所示。

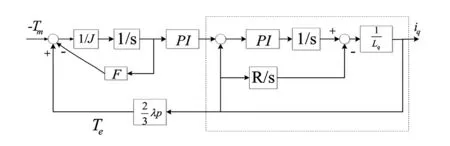
图4 q轴电流等效传递函数框图

根据式(4)所表述的q轴电流方程建立图4虚线框中的电流内环。这里采用了idref≡0的控制方式，因此，在q轴电流内环的传递函数中不再表述d轴电流分量在q轴电流的耦合项。由于静止坐标与旋转坐标的Clark和Park变换只是数学上的理论变换，并且其变换的依据正是基于功率不变的约束，因此在q轴等效的传递函数中不需要列写Clark和Park变换环节。

以图4中左侧PI控制器的输出作为电流内环的输入，q轴电流分量iq作为输出，可得q轴电流内环的传递函数为

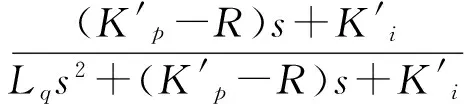
(7)

图4中虚线框之外的系统为q轴电流矢量的转速外环，其输入量为机械扭矩Tm，输出为电磁扭矩Te，将输出的电磁扭矩作为扭矩输入的参考值送入速度内环，从而建立速度外环与电流内环之间的联系。从图4可以看出，q轴的电流内环是单输入单输出(SISO)的系统，将其作为一个传递函数模块加入到速度外环的模型中，见图5，可得双闭环传递函数。

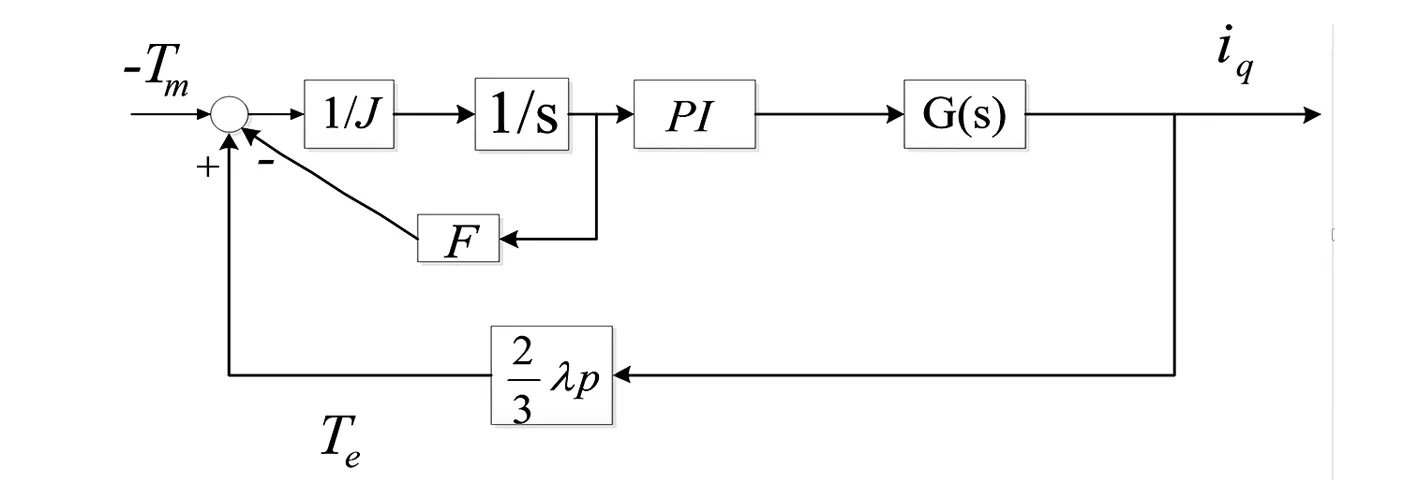
图5 q轴矢量控制的速度外环

令M(s)为前向通道的传递函数，q轴速度外环传递函数方程为

(8)

对式(8)进行化简，得到全系统的闭环传递函数为

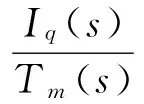
(9)

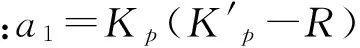
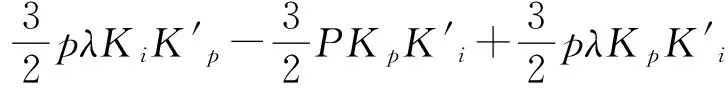
稳定作为控制系统重要的性能指标，也作为系统能够正常运行的首要条件，如果系统不稳定，就会在任何微小扰动作用下偏离原来的平衡状态，并随着时间的推移而发散。任何系统在扰动的作用下，都会发生偏离平衡状态的现象，产生偏差。因而，分析系统的稳定性是控制理论的基本任务之一。对于一阶或二阶系统，可以通过求解系统特征根的方法来判定系统的稳定性，但高阶系统的求根工作量是很大的[11]。通常的方法是借助劳斯稳定判据来判定高阶系统的稳定性。

由式(9)可知PMSM全系统的特征函数为

H(s)=b1s4+b2s3+b3s2+b4s+b5

(10)

列写系统的劳斯表如表1所示。

表1 PMSG q轴电流传递函数劳斯表

根据永磁同步电机的参数，由劳斯稳定判据的充要条件求解劳斯表中的第一列元素，使其全部大于0，即可得到转速内环和电流外环的PI参数范围。d轴电流分量采用的相同的方法，具体的整定过程不再赘述。

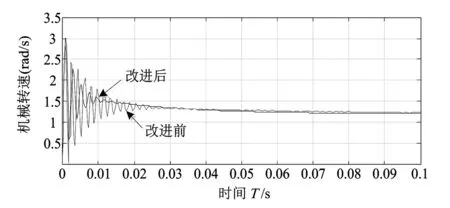
(a)转速波形

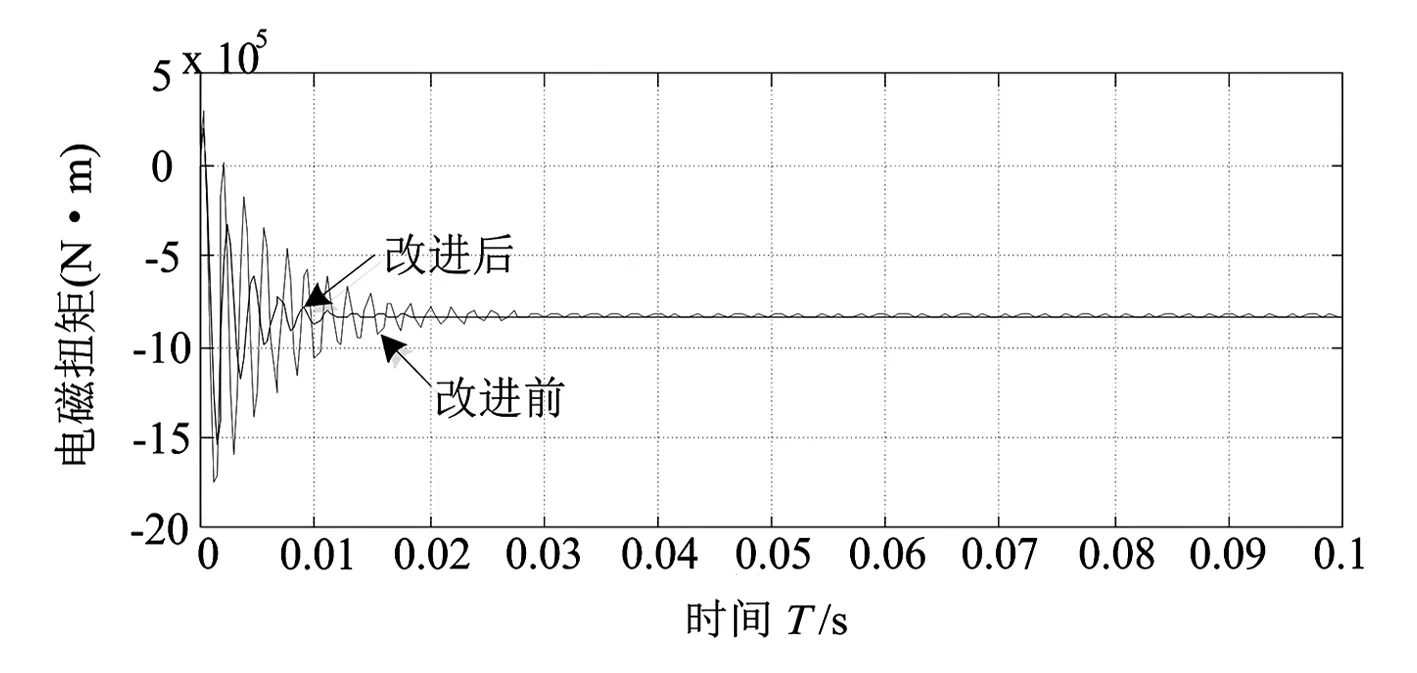
(b)电磁扭矩波形

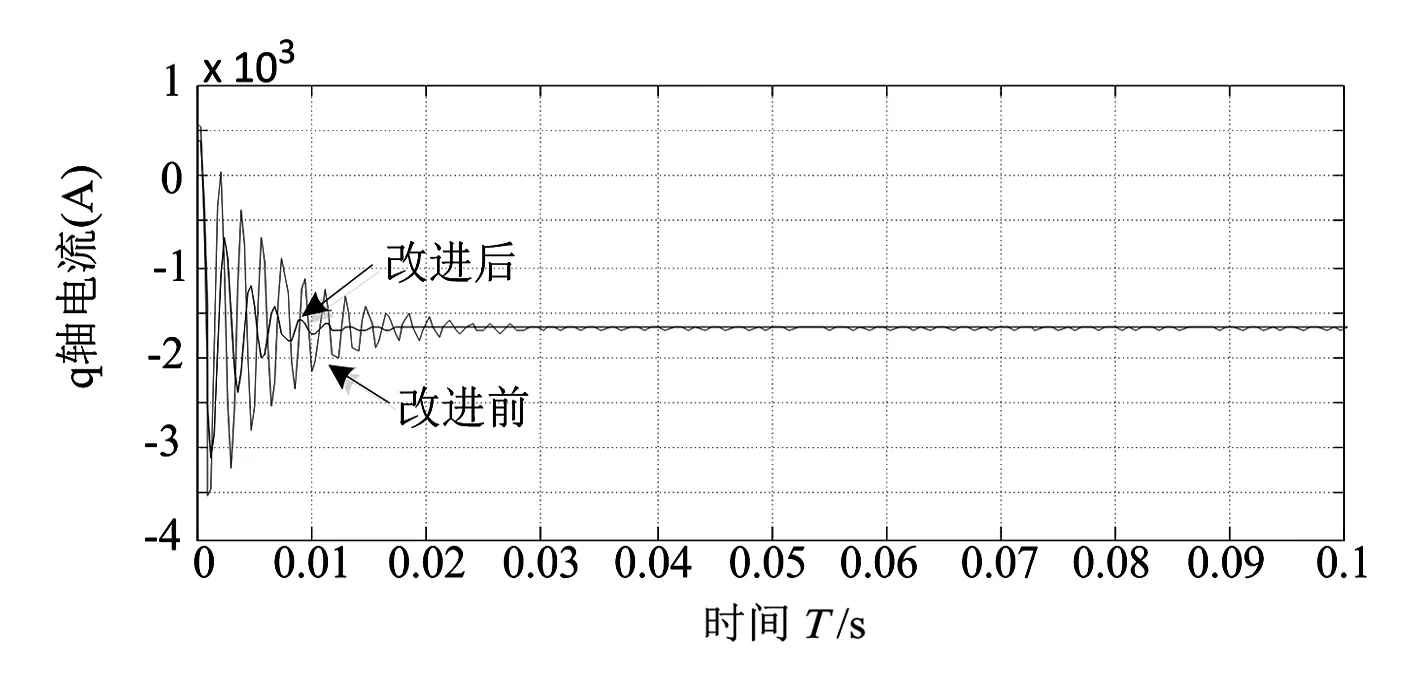
(c)q轴电流波形

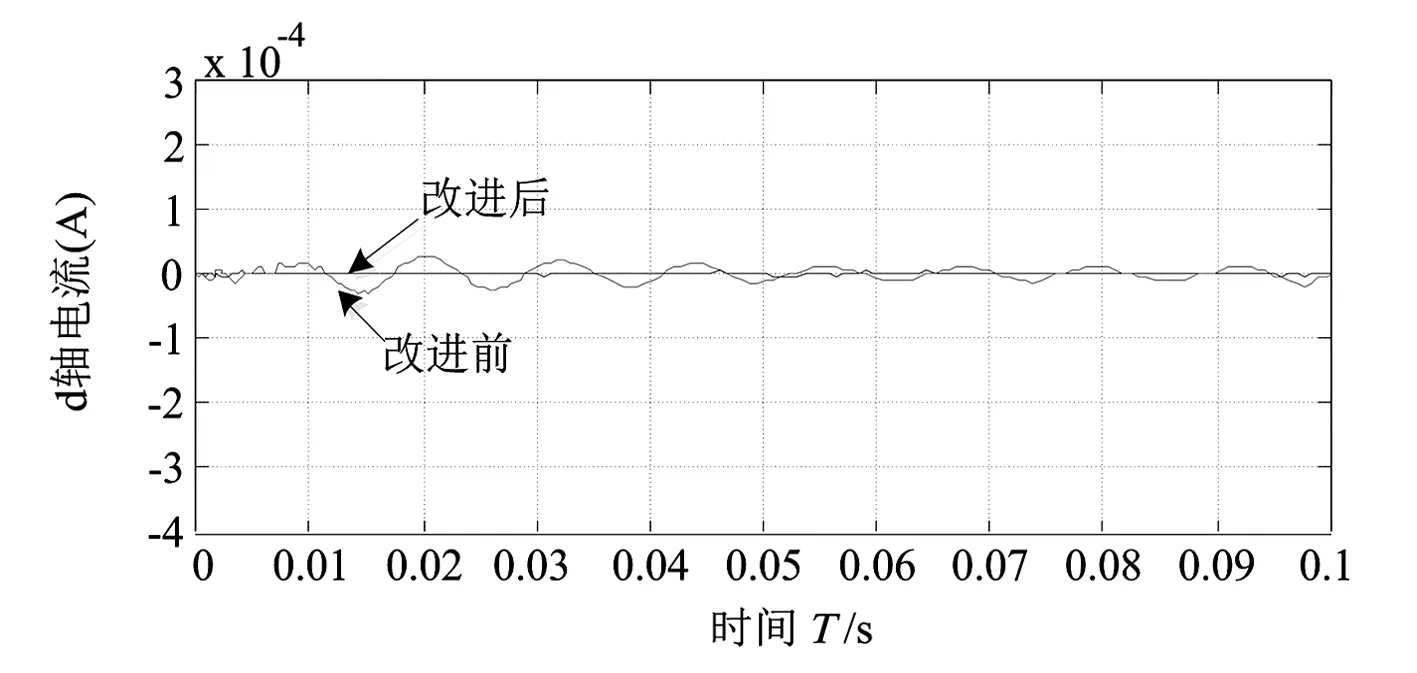
(d)d轴电流波形

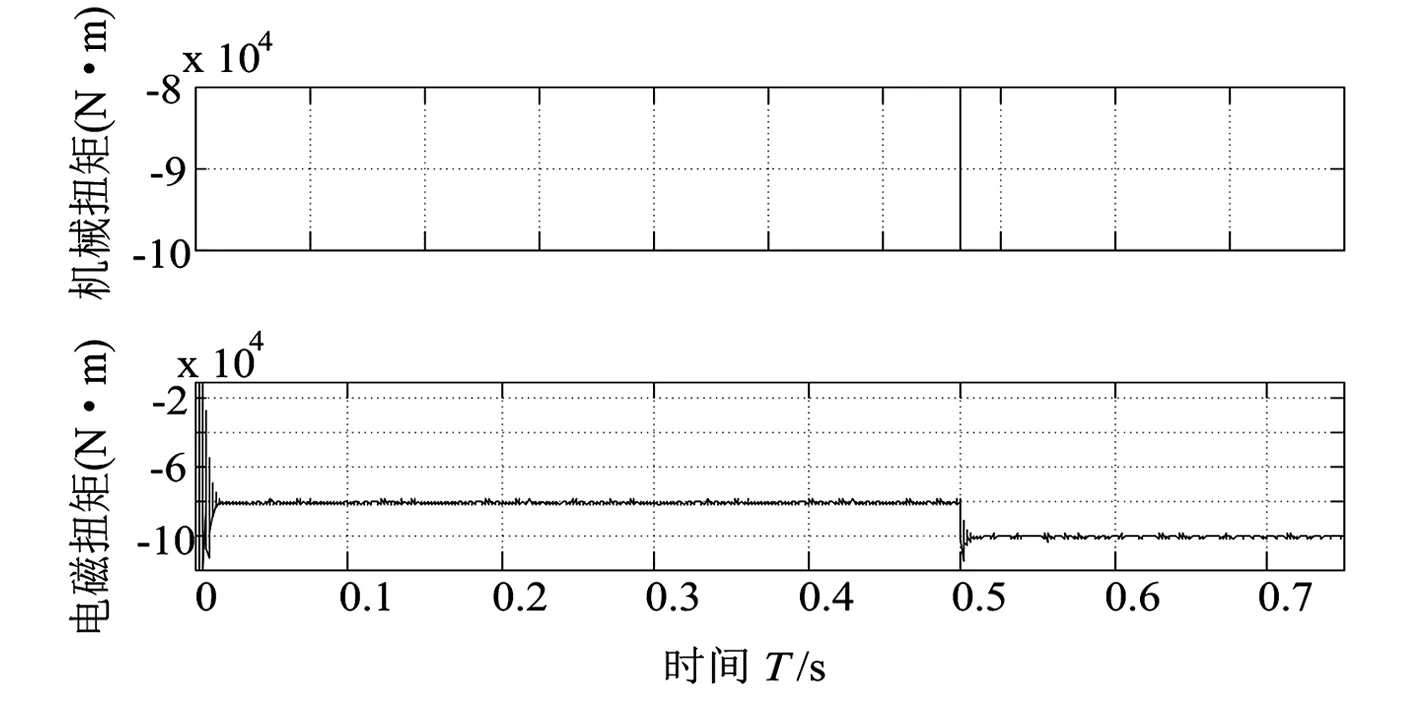
(e)机械扭矩变形波图6 仿真波形

4 仿真验证及分析

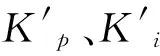
运行仿真模型，得到PMSM的机械转速、电磁扭矩以及d轴与q轴的电流波形。为了测定整定得到的PI参数对系统输入量发生突变时的鲁棒性以及其对扭矩变化的响应速度，在PMSM系统稳定运行0.5 s时，使电机的机械扭矩发生跃变，观测其在参数跃变后的扭矩波动的波形。仿真波形见图6。

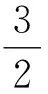
相比改进前的控制策略，改进后的前馈解耦控制方案，对d轴和q轴之间的耦合量pωiq、-pωiq与λpω/Lq进行了补偿，使d轴和q轴分量中不再出现耦合项。

4 结 论

在分析传统控制方法的基础上，考虑到d轴和q轴的耦合，提出前馈解耦的控制策略，并针对前馈解耦补偿控制的PMSM全系统进行了分析，得出了基于q轴电流分量的双闭环系统与PMSM数学模型之间的联系以及简化的传递函数模型。由于其传递函数为高阶方程，控制理论中针对一阶和二阶的求解特征根的方法已不再适用，提出利用劳斯稳定判据来整定控制器参数范围的方法。仿真结果表明，依据得出的全系统简化传递函数能够有效实现控制目标，并且在输入量发生变化时，能使系统快速达到稳定状态并对系统变化有较好的鲁棒性。然而基于劳斯稳定判据整定的PI参数，并不能得到精确的比例和积分参数，需要进行多次的调试是所提方法需要改进的研究方向。

[1] 李政，胡广大，崔家瑞，等.永磁同步电机调速系统的积分型滑模变结构控制[J].中国电机工程学报，2014，34(3)：431-437．

[2] 耿翠红，曹以龙.基于DSP的PMSM矢量控制系统的硬件和软件实现[J].电力电容器与无功补偿，2014，35(1)：30-33．

[3] 郭磊磊，张兴，杨淑英，等.一种改进的永磁同步发电机模型预测直接转矩控制方法[J].中国电机工程学报，2016，36(18)：1-9．

[4] Bimal K.Bose.现代电力电子学与交流传动[M].北京：机械工业出版社，2005．

[5] 唐小琦，白玉成，陈吉红.永磁同步电机高性能电流解耦控制的研究[J]．电气传动，2009，39(10)：18-22．

[6] 陈荣．永磁同步电机控制系统[M].北京：中国水利水电出版社，2009．

[7] P Krause，O Wasynczuk，S Sudhoff，et al．Analysis of Electric Machinery and Drive Systems[M]．IEEE Press，2002．

[8] D Grenier,L A Dessaint，O Akhrif，et al． Experimental Nonlinear Torque Control of a Permanent-magnet Synchronous Motor Using Saliency[J].IEEE Transactions on Industrial Electronics,1997,44(5):680-687．

[9] 李三东，薛花，纪志成．基于Matlab永磁同步电机控制系统的仿真建模[J]．江南大学学报(自然科学版)，2004，3(2)：115-120．

[10] 黄知超，杨升振，延红艳，等.基于dq坐标系有功无功电流解耦空间电压矢量的STATCOM控制方法[J].电测与仪表，2012，49(12)：32-36．

[11] 胡寿松.自动控制原理[M]．北京：科学出版社，2008．

[12] 黄一，张文革．自抗扰控制器的发展[J]．控制理论与应用，2002，19(4)：485-492.

As the feedforward decoupling of permanent magnet synchronous motor (PMSM) adopts double closed-loop controller, its system-wide transfer function is higher than that of second order, which leads to the difficulty of controller parameter setting. By analyzing the mathematical model of velocity loop and current loop of PMSM and its decoupling control, the relationship between the control quantity and the mathematical model of PMSM in double closed-loop controller is obtained, and the whole system based on Laplace transform is constructed, which provides a theoretical basis for the PI parameter setting of double closed-loop controller. Aiming at the high-order characteristic of the constructed system-wide transfer function model, the range of PI parameters is set according to Rouse stability criterion, and the experimental simulation is carried out in Simulink. The simulation results show that the parameters after setting can make the system become stable quickly and have good robustness.

permanent magnet synchronous motor (PMSM); feedforward decoupling; simplified model; Routh stability criterion

国家自然科学基金项目(51667020)

TM351

：A

：1003-6954(2017)04-0074-05

2017-03-04)

荆世博(1989)，硕士研究生，主要研究方向为可再生能源并网技术； 王维庆(1959)，博士、教授、博士生导师，研究方向为电力系统自动化和风力发电机组的智能控制。