恒定电流密绕椭球形线圈磁场的空间分布

林佩珠，刘家明，江俊勤

(广东第二师范学院 物理与信息工程系，广东 广州 510303)

恒定电流密绕椭球形线圈磁场的空间分布

林佩珠，刘家明，江俊勤

(广东第二师范学院 物理与信息工程系，广东 广州 510303)

从毕奥-萨伐尔定律出发，推导出密绕在旋转椭球面上载流线圈磁场的积分计算式. 利用Mathematica-10先对方位角φ积分并将结果表达为第一类和第二类完全椭圆积分的线性组合, 进而绘制出形象直观、高精确度的磁场三维分布图. 数值结果直观地表明:椭球内部全空间的磁场是均匀的，磁感应强度处处大小相等、方向相同；当nI值一定时，长轴与短轴的比值b/a越大, 椭球内磁场越强.

磁场；线圈；空间分布;椭圆积分；Mathematica-10

匀强磁场在物理学的理论分析和实验仪器中都起着重要的作用，如何有效地产生匀强磁场一直是人们关心的问题[1-7].亥姆霍兹线圈和共轴三线圈的结构简单[1-4]，但磁场的均匀性较差；有限长恒定电流圆柱形螺线管磁场的均匀性有了较大改善，但在比较接近端口处均匀性仍然不好[5]. R.P.费恩曼在其物理学讲义[6]中提及在旋转椭球面上沿着轴线方向均匀缠绕线圈可以在其内部产生均匀磁场,但由于数学的复杂性，至今未见有文献全面准确地分析该磁场的空间分布，例如文献[7]虽然进行过研究，但只限于讨论球形线圈(并非文献[5]所述的一般旋转椭球形线圈)，其结果表达式已经十分复杂而且是近似的、未能绘制出磁场的空间分布图.

本文将文献[8]提出的研究带电圆环片电场空间分布的方法推广应用于研究载流椭球形线圈磁场的空间分布. 从毕奥-萨伐尔定律出发，利用Mathematic10的符号运算和数值计算能力及绘图功能，先把对方位角的积分表达为第一类和第二类完全椭圆积分，然后用数值分析的方法全面、高精度地研究密绕在旋转椭球面上载流线圈磁场的空间分布，包括:在椭球内空间的磁场是否处处均匀，椭球内空间的磁感应强度与椭球几何形状的关系．

1 椭球形密绕线圈磁场的积分计算式

线圈缠绕在旋转椭球面上，沿着z轴单位长度的匝数为n，椭球面方程为

(1)

图1 椭球形线圈

由于具有轴对称性，只需研究xoz平面上任一点P(x,0,z)的磁场分布，即xoz平面上磁场的分布代表了任何过z轴平面上的磁场分布情况.

在柱坐标系中，电流元Idl′的位矢可写为

r=ρcosφi+ρsinφj+z′k，

φ为方位角，0≤φ≤2π，观测点P(x,0,z)相对于电流元Idl′的位矢R和距离R分别为

R=(xi+zk)-r=(x-ρcosφ)i-ρsinφj+(z-z′)k,

而

dl′=(-ρsinφi+ρcosφj)dφ，

所以

[ρcos φ(z-z′)i+ρsin φ(z-z′)j+

把R和dl′×R代入毕奥-萨伐尔定律，z′～z′+dz′内包含的匝数为dN=ndz′，先对φ积分得

(2)

式中

(3)

(4)

(5)

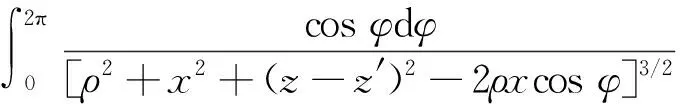
(6)

式(2)显示，xoz平面内的磁场没有y分量，这是因为

由式(2)～(6)得到的是位于z′～z′+dz′内ndz′匝圆形线圈所产生的磁场，再对z′积分就得到载流椭球形线圈产生的总磁场

通过监测分析石化企业中一台驱动离心压缩机组的汽轮机，设计工作转速6 500r/min，一阶临界转速：4 020r/min，二阶临界转速：8 150r/min，多块可倾滑动轴瓦，迷宫密封，入口蒸汽压力：3.8MPa，出口蒸汽压力：0.008MPa，振动报警值—峰峰值38μm，振动停机值-峰峰值65μm。

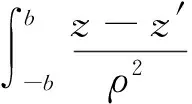
(7)

(8)

(5)～(8)可以确定空间任一点的磁场.

2 椭圆积分、数值分析、磁场的空间分布

磁感应强度计算式(7)～(8)是十分复杂的二重积分，无法做解析计算. 本文使用Mathematica进行数值计算和绘图，用直观形象的方式研究磁场的空间分布，但是如果直接使用二重数值积分，因其计算量过于庞大而难以进行. 经研究发现：可以把式(5)和式(6)的2个积分α和β表达为第一类和第二类完全椭圆积分(对z′才使用数值积分):

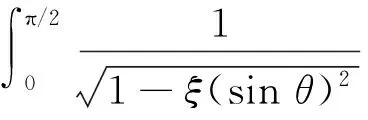
(9)

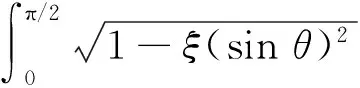
(10)

用人工方法把α和β化为椭圆积分，其过程将十分繁琐，故使用Mathematica-10进行计算，可得：

(11)

(12)

式中EllipticK(ξ)和EllipticE(ξ)为式(9)和式(10)所定义的第一类和第二类完全椭圆积分.

1)当b=2a时，B的分布如图2所示,|Bz|的分布如图3所示.

图2 当b=2a时B的分布图

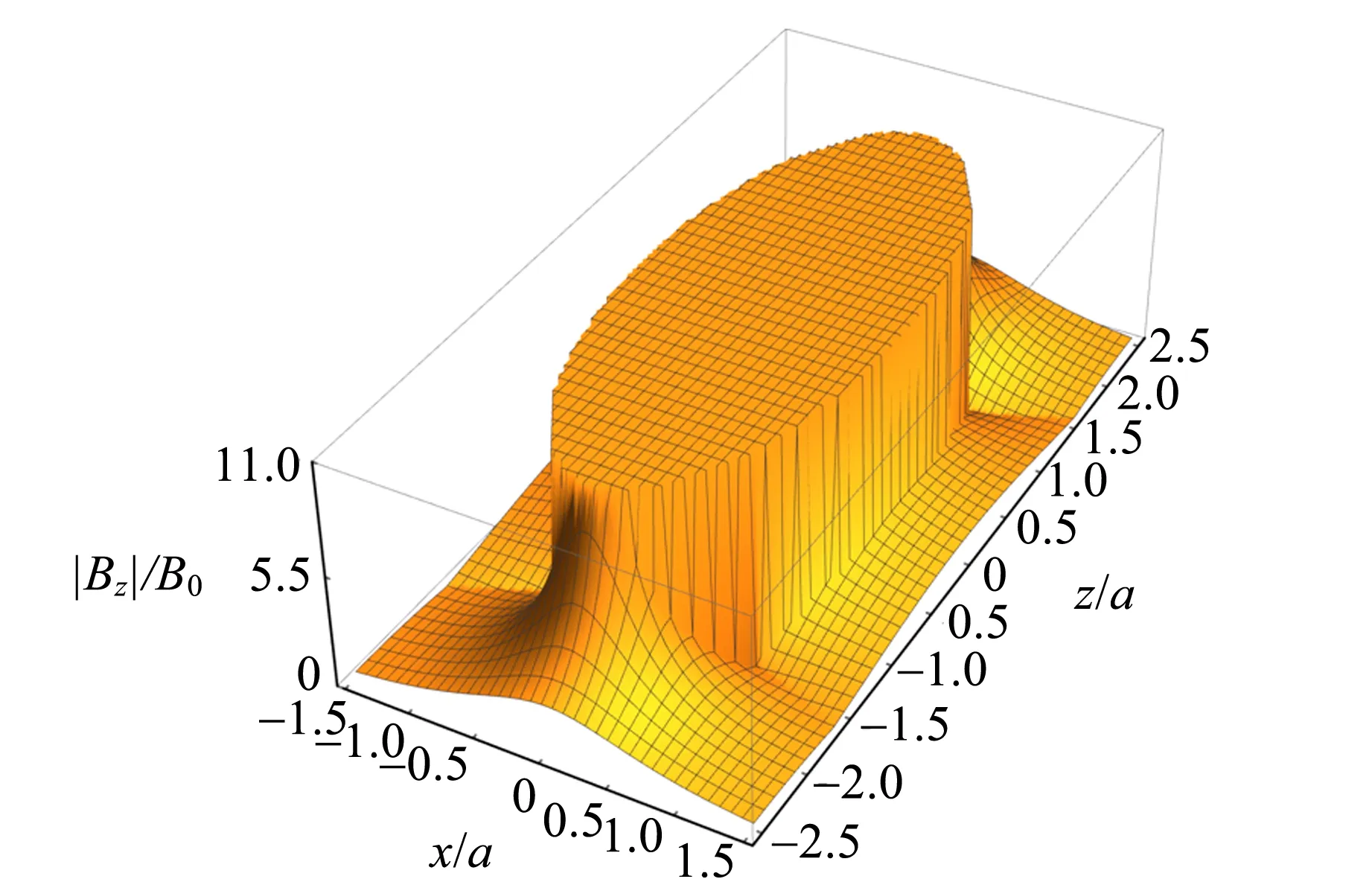
图3 当b=2a时|Bz|的分布图

图4 当b=1.5a时B的分布图

图5 当b=1.5a时|Bz|的分布图

3)当b=a时，B的分布如图6所示,|Bz|的分布如图7所示.

图6 当b=a时B的分布图

图7 当b=a时|Bz|的分布图

3 结 论

从毕奥-萨伐尔定律出发，推导了密绕在旋转椭球面上载流线圈磁场的积分计算式. 利用Mathematica-10符号运算和数值计算能力及数字绘图功能，先把对方位角的积分结果表达为第一类和第二类完全椭圆积分的线性组合,进而绘制了磁场的三维分布图，直观呈现了磁场的性质.

1) 椭球内部全空间的磁场是均匀的. 图2～7中，椭球内部磁感应强度处处大小相等;椭球内部B的分布与|Bz|的分布完全相同，这说明椭球内部的磁场全部来自z分量的贡献，即磁场方向全部为旋转对称轴方向.

2) 当nI一定时，长轴与短轴的比值b/a越大, 椭球内磁场越强. 详细的数值结果为:

a.当b=2a时，

(13)

b.当b=1.5a时，

(14)

c.当b=a时，

(15)

由此可见,长旋转椭球形线圈优于球形线圈，它不但在制作上易于缠绕，而且在相同的nI值情况下长旋转椭球形线圈的磁场大于球形线圈和扁旋转椭球形线圈的磁场.

[1] 王森，罗成． 亥姆霍兹线圈磁场的均匀性分析[J]． 大学物理，1998,17(3)：17-20.

[2] 曾晓英. 亥姆霍兹线圈磁场的均匀性分析及误差估

算[J]. 物理实验，2000，20(5)：38-39.

[3] 江俊勤. 亥姆霍兹线圈磁场均匀性的研究[J]． 广东教育学院学报,2006,26(5)：61-66.

[4] 陈俊斌,朱霞,张甫治. 用等均匀性曲面研究共轴三线圈磁场的均匀性[J]． 大学物理，2007，26(3)：18-21.

[5] 江俊勤. 基于Mathematica的数字化物理学[M]. 北京：科学出版社，2015:78-104.

[6] 费恩曼R P，莱登R B，桑兹M. 费恩曼物理学讲义(第2卷)[M]． 李洪芳，王子辅，钟万蘅,译. 上海：上海科学技术出版社，2013:397.

[7] 于凤军． 球形线圈磁场均匀性的研究[J]． 大学物理，2012，31(6)：13-16.

[8] 江俊勤. 带电薄圆环片电场的空间分布[J]． 安徽师范大学学报，2016，39(4)：434-436.

[9] 郭玉川，庹晏斌，文小辉，等. 改进型赫姆霍兹线圈磁场均匀性及实用性分析[J]. 物理实验，2015，35(11):42-46.

[责任编辑：尹冬梅]

Magneticfieldofsteadycurrenttightlywoundellipsoidalcoil

LIN Pei-zhu, LIU Jia-ming, JIANG Jun-qin

(Department of Physics and Information Engineering, Guangdong University of Education, Guangzhou 510303, China)

Based on the Biot-Savart law, an integral expression of the magnetic field induced by steady current tightly wound ellipsoidal coil was derived. Using the Mathematica-10, an integral result for the azimuth angle was expressed as the linear combination of the first and the second kinds of complete elliptic integral, and then three-dimensional maps of the distribution of the magnetic field were plotted. The results showed：1) Inside the ellipsoidal coil, the magnetic field was uniform; 2) The bigger the ratio of the long axis and the short axis, the stronger was the magnetic field.

magnetic field; coil; spatial distribution; elliptic integral; Mathematica-10

2016-10-31

广东省高等学校物理专业综合改革试点项目(No.XM060012物理学9010-15281)

林佩珠(1968-)，女，广东揭阳人，广东第二师范学院物理系实验师，学士，主要从事大学物理实验教学与研究工作.

O441

：A

：1005-4642(2017)09-0012-04